“운영체제 : 아주 쉬운 세가지 이야기”를 읽으면서 핵심 내용을 정리하였습니다.
이화여대 반효경 교수님의 운영체제 강의를 듣고 복습 차원에서 책 한권을 완독해보고자 합니다.
잘못된 정보가 있다면 댓글 남겨주시면 감사하겠습니다!
동적 재배치의 한계
지금까지 메모리를 가상화하는데 필요한 주소변환의 원리에 대해 알아 보았다. 동적 재배치라는 하드웨어의 지원을 받아 주소를 변환하는 방법은 간단하였지만 다음과 같은 한계가 있었다.
1.
프로그램의 전체 주소공간을 물리 메모리에 탑재하여 발생하는 내부 단편화
•
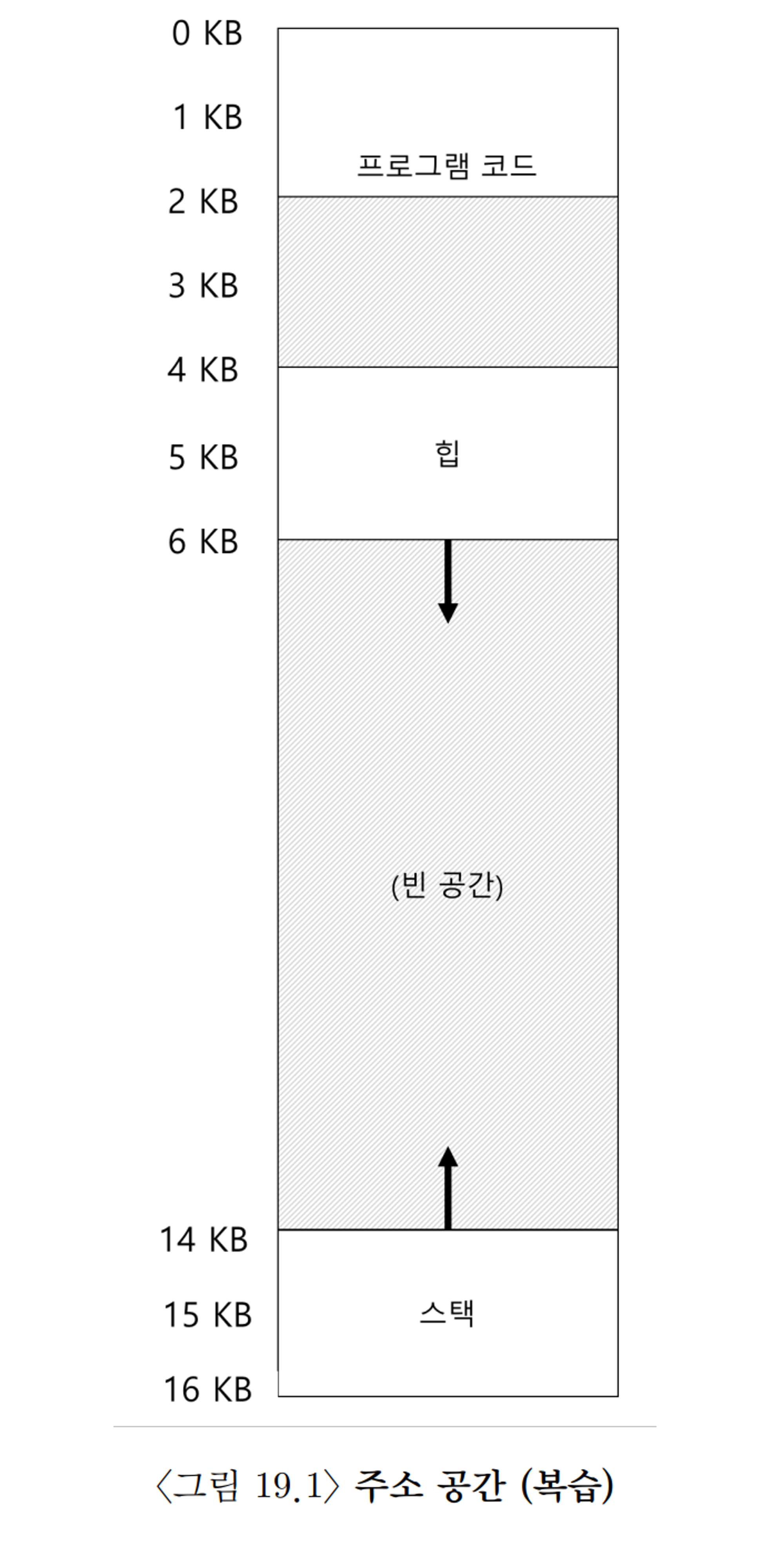
상기 그림의 힙과 스택사이의 큰 빈공간
•
그림의 예시는 작은 주소 공간을 가정하였지만 32비트 컴퓨터의 경우 4GB의 주소공간을 가지고 있다
•
프로그램은 실제 수 메가바이트에 그치지만 4GB를 모두 물리메모리에 올려야해서 유연성이 떨어짐
세그멘 테이션의 등장 : 베이스/바운드의 일반화
상기 한계를 극복하기 위해 세그멘테이션이 등장하게 되었다. MMU안에 한쌍의 베이스 바운드 쌍만 존재 하는 것이 아니라 주소공간의 논리적인 단위인 세그먼트의 갯수 만큼 여러 쌍의 베이스/바운드 레이스터를 가지고 있게 된다.
•
대표적인 세그먼트 : 코드, 스택, 힙
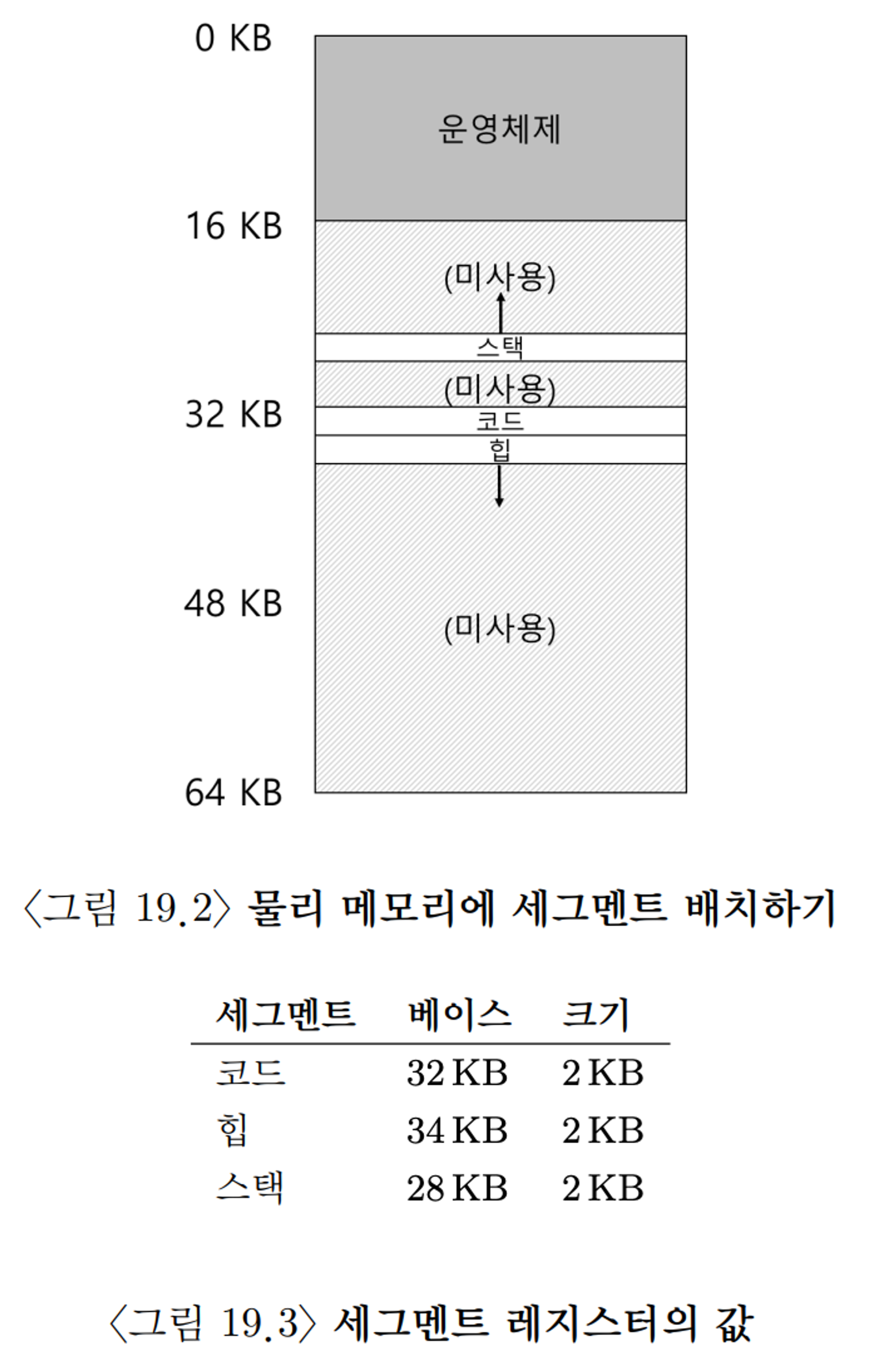
이로써 운영체제는 아래와 같이 물리 메모리의 각기 다른 위치에 세그멘테이션을 배치 할 수 있게 됨으로서 내부 단편화를 방지할 수 있게 되었다.
만약 그림 19.1에서 힙의 가상 주소 공간인 4200번지를 물리주소로 변환하기 위해서는 가상 주소공간에서 힙의 시작위치(4096, 4KB) 부터 떨어진 오프셋(104)을 구하고 그것을 힙의 베이스 레지스터에 더해 주면 된다.
세그먼트 폴트
세그멘트 종류의 파악
하드웨어는 가상 주소를 보고 세그먼트의 종류가 무엇인지 알 수 있어야 하고 해당 세그먼트안에서 오프셋이 얼마인지 알수 있어야 한다.
•
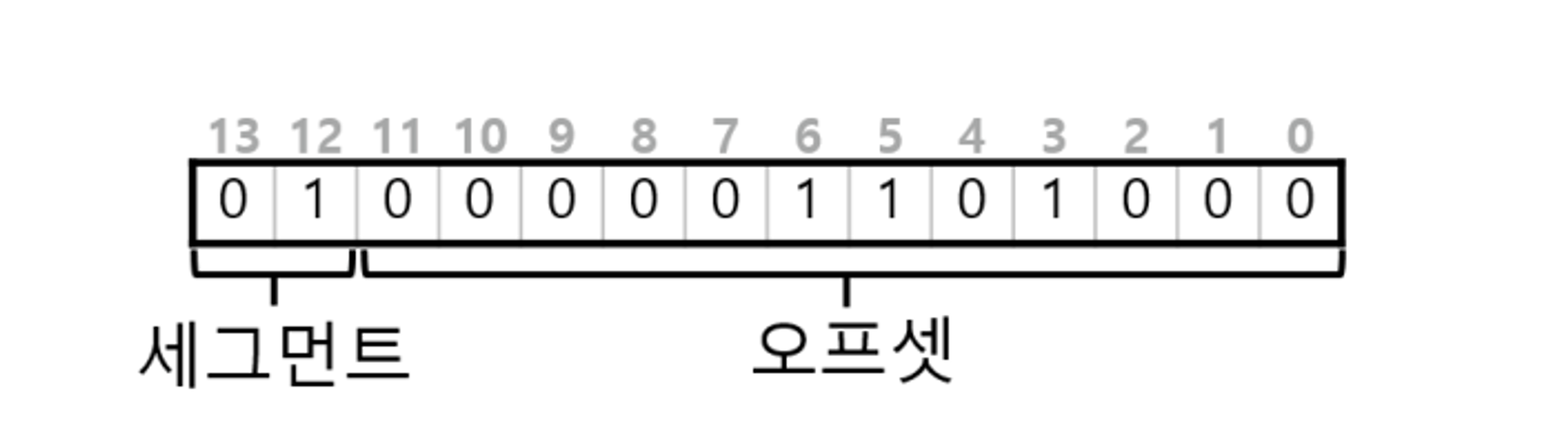
16KB의 가상주소공간을 가정하였으므로 14비트로 주소를 나타낼 수 있다.
•
상위 2비트는 세그먼트의 종류를 나타낸다
•
하위 12비트는 오프셋을 나타낸다
•
오프셋이 바운드보단 작은지 검사하여 유효한 주소인지 검사한다
//14bit VA중 2bit 얻어오기// SEG_MASK = 2, SEG_SHIFT = 12, OFFSET_MASK = 0xFFF
segment = (virtualaddr & SEG_MASK) >> SEG_SHIFT
// offset 얻어오기
offset = virtualaddr & OFFSET_MASK
// 예외 검사if (offset >= bound[segment])
raiseExpection(PROTECTION_FAULT)
else
physaddr = base[segment] + offset
register = accessMemory(physaddr)
Plain Text
복사
스택
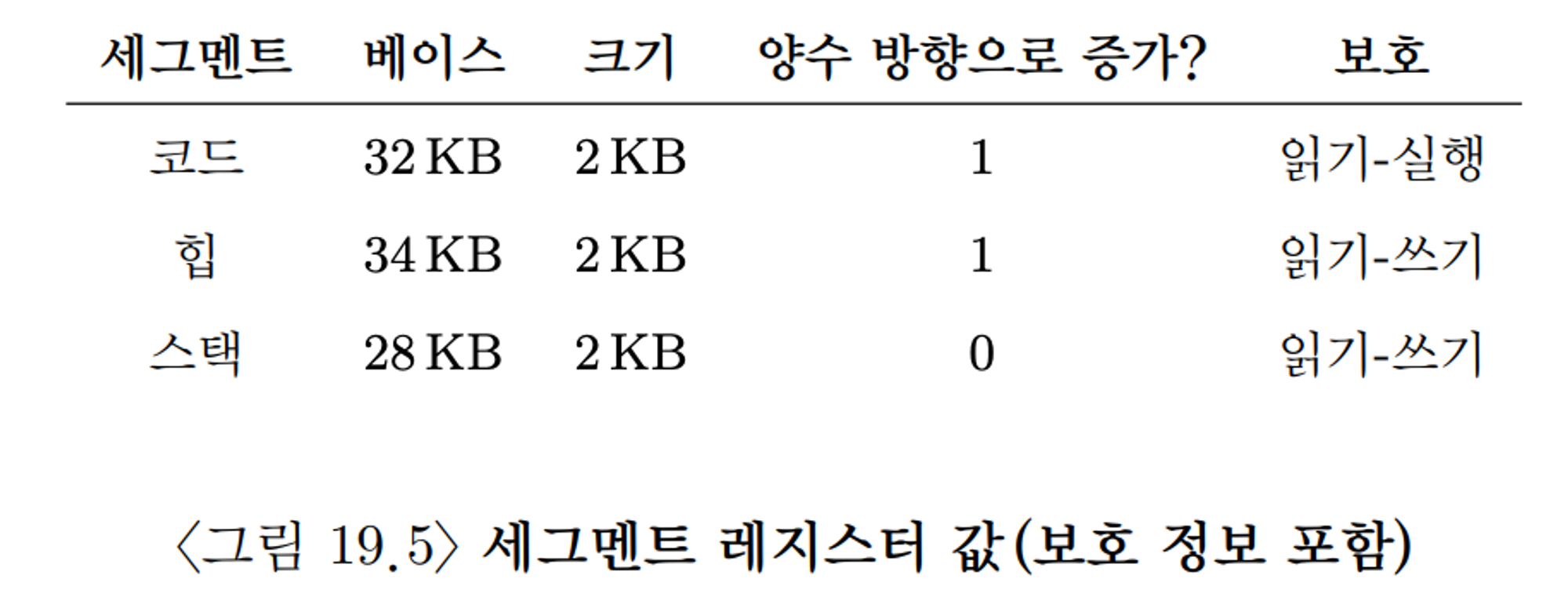
스택의 경우 다른 세크멘트와 다르게 주소가 감소하는 방향으로 늘어난다. 따라서 하드웨어는 세그먼트가 주소공간 내에서 확장하는 방향에 대해서도 알고 있어야 한다. 이를 위해 하나의 비트를 사용하여 양의 방향과 음의 방향을 구분 한다. 방향에 따라 주소 공간을 변환하는 방법이 달라진다.
공유 지원
메모리를 절약하기 위해 간단한 하드웨어 자원을 통해 메모리 세그멘트를 공유할 수 있게 되었다. 특히 코드영역 공유는 현재 시스템에서도 광범위하게 사용 중이다.
protection bit를 추가하여 읽기/쓰기/실행과 같은 권한을 설정 할 수 있다. 권한을 설정할 수 있게 되면 코드 세그먼트를 읽기 권한으로 설정하면 주소 공간의 독립성을 유지하면서도 여러 프로세스가 주소 공간의 일부를 안전하게 공유할 수 있게 된다.
•
세그멘테이션의 한계
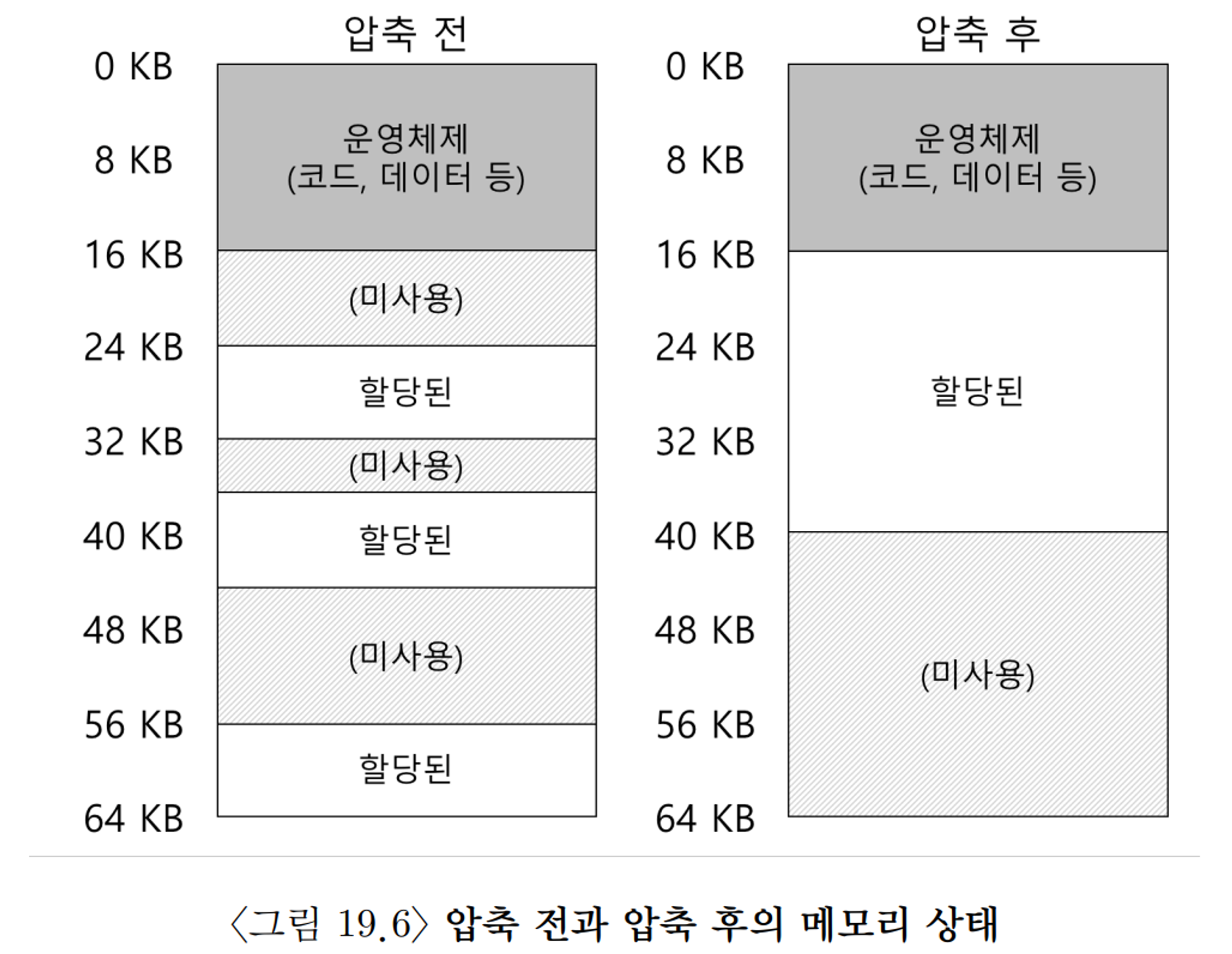
세그멘테이션은 내부 단편화는 해결하였지만 각 세그멘트의 크기가 일정하지 않기 때문에 아래 그림의 왼쪽과 같은 외부 단편화를 유발하여물리 메모리 내에 작은 빈공간들이 계속 생기게 된다.
압축을 사용하면 어느정도 문제를 해결할 수 있지만 세그먼트를 복사하여 새로운 곳으로 이동 시키는 것은 메모리 부하가 큰 연산이고 상당량의 프로세서 시간을 사용하기 때문에 비용이 많이 들게 된다.
빈공간 리스트를 관리하는 알고리즘을 사용하면 어느정도 문제를 해결할 수 있지만 아무리 좋은 알고리즘이라도 여전히 외부 단편화는 존재하게 된다.
이를 해결하기 위헤 페이징이라는 기법이 등장하게 되었고 다음 시간에 해당 내용에 대해 알아보려고 한다.