누적합
카카오 블라인드 공채에서는 2년간 누적합을 활용하는 문제가 출제되었습니다.
•
•
또 한 번 나오기 쉽지 않겠지만, 누적합이 어떤 유형의 문제를 효율적으로 해결할 수 있는지 살펴보도록 하겠습니다.
누적합이란?
누적합은 구간의 변화를 효율적으로 처리할 수 있는 알고리즘입니다.
광고 삽입 문제로 살펴보기
•
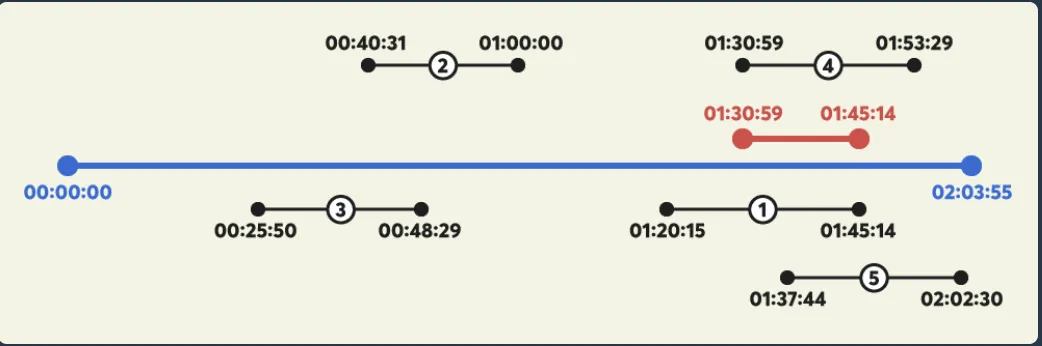
광고를 삽입 했을때, 최적의 광고 위치(구간)을 구하도록 요구합니다.
•
최적의 광고 위치를 선정하는데 활용되는 요소로
◦
시청자 재생 구간 정보 logs
▪
log 하나는 시청시작시간 & 시청종료시간으로 구성
◦
광고의 길이
여기서 시청자의 재생 구간 정보 logs를 가공하는 과정에서 누적합을 적용할 수 있습니다.
누적합을 적용하지 않는 다면, 매 log당 시청시간만큼의 연산이 필요합니다.
누적합을 적용한다면, 매 log당 2번의 연산과 마지막에 전체를 순회하며 누적을 구하는 2 * N번의 연산만이 필요합니다.
파괴되지 않은 건물 문제로 살펴보기
•
매 이벤트의 누적 결과 파괴되지 않은 건물의 숫자를 구하도록 요구합니다.
•
스킬에 의해 건물의 내구도에 변화가 일어납니다.
◦
스킬 정보가 담긴 skill
▪
스킬 하나는 type & 적용 범위로 구성
건물의 내구도에 스킬의 작용을 누적하여 적용할때, 누적합을 활용할 수 있습니다.
누적합을 적용하지 않는 다면, 매 스킬당 적용 범위 크기만큼의 연산이 필요합니다.
누적합을 적용한다면, 매 스킬당 4번의 연산과 마지막에 전체를 순회하며 누적을 구하는 2 * N * M번의 연산만이 필요합니다.
코드로 살펴보기
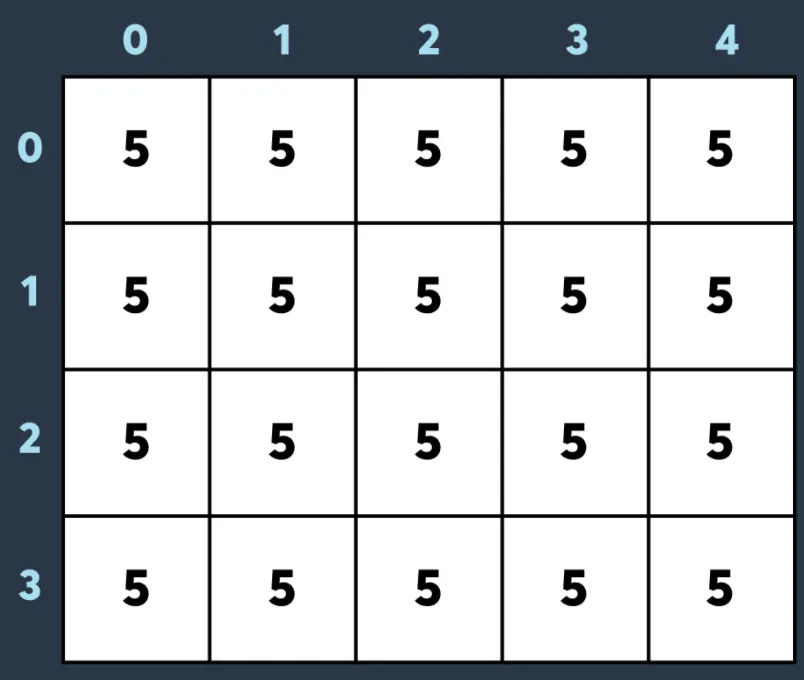
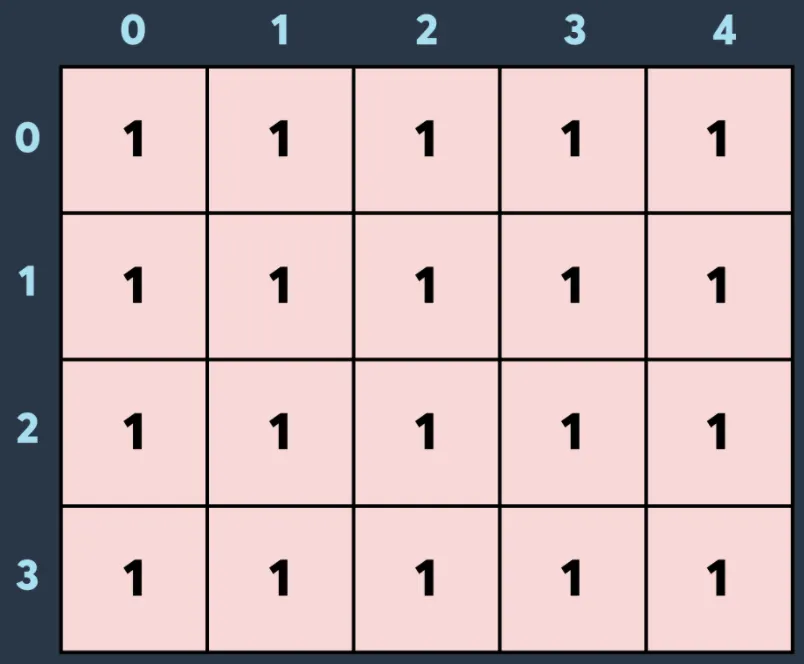
데이터 가공하기
// 1차원 누적합의 경우
// x0부터 x1까지 v 더하기
arr[x0] += v;
arr[x1 + 1] -= v;
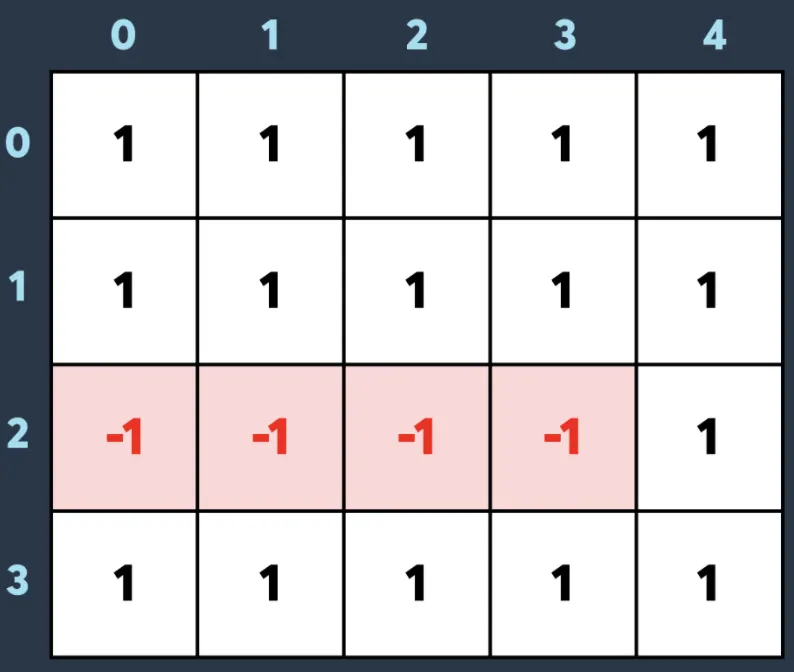
// 2차원 누적합
// (r0, c0)부터 (r1, c1) 까지 v 더하기
arr[r0][c0] += v;
arr[r0][c1 + 1] -= v;
arr[r1 + 1][c0] -= v;
arr[r1 + 1][c1 + 1] += v;
C
복사
종말 단계에서 누적합 계산하기
// 1차원 누적합
for (int x = 1; x < arr_length; x++)
arr[x] += arr[x - 1];
// 2차원 누적합
// 행 or 열 각각의 방향에 대해서 누적합 진행
for (int r = 0; r < r_end; r++)
for (int c = 1; c < c_end; c++)
arr[r][c] += arr[r][c - 1];
for (int c = 0; < c_end; c++)
for (int r = 1; r < r_end; r++)
arr[r][c] += arr[r - 1][c];
C
복사
누적합에서 특정 구간의 구간합 계산하기
// 인덱스 초과에 대한 코드는 기재하지 않았으나 필요
// 1차원 구간합
result = arr[x1] - arr[x0 - 1];
// 2차원 구간합
result = arr[r1][c1] - arr[r0 - 1][c1] - arr[r1][c0 -1] + arr[r0 - 1][c0 - 1]
C
복사