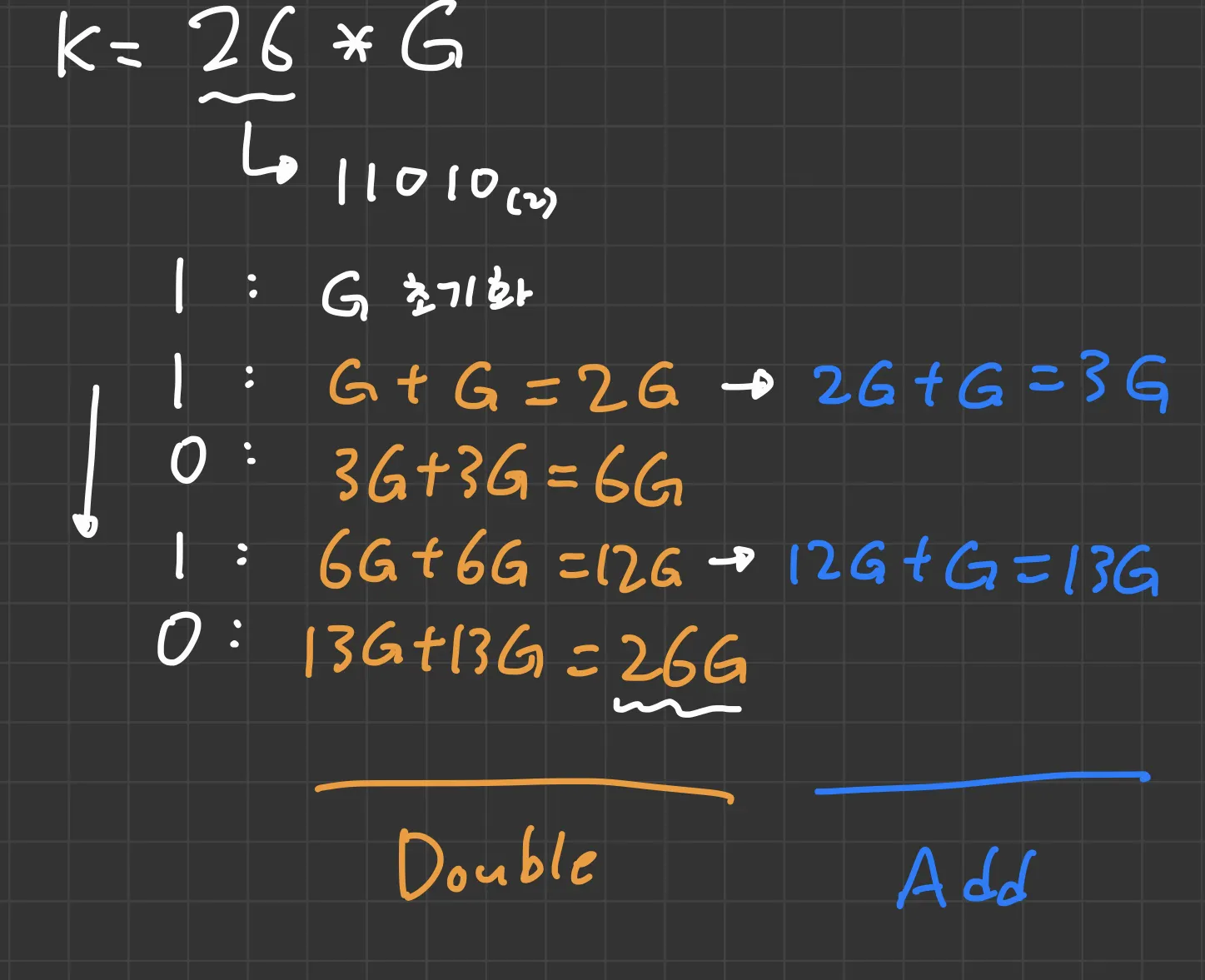//////
Search
Duplicate
🔒

2주차 - 비대칭키 암호화

생성일
2022/03/14 05:30
과목
블록체인

비대칭 키 암호화

개인 키와 공개 키 두 키를 한 쌍으로 암호키를 구성한다.
•
개인 키 (Private key) : 개인이 보관
•
공개 키 (Public key) : 타인에게 공개

비대칭 키를 이용한 응용 분야

•
비밀 메세지 : A의 공개 키로 암호화한 메세지는 A의 개인 키로 풀 수 있음
•
전자 서명 : A의 공개 키로 풀리면 A의 개인 키로 암호화 한 것이라는 증거

대칭 키와 비대칭 키 암호화의 차이

대칭 키 암호화
비대칭 키 암호화
개념적 차이
키를 송/수신자가 공유
키를 공유하지 않고 각자 보존
키 구성의 차이
하나의 비밀 키를 공유
개인 키와 공유 키가 존재
구성원의 수가 n
비밀 키 = n(n - 1) / 2
개인 키 n개, 공유 키 n개
암호 방식의 차이
기호를 대체, 치환 기반
숫자를 다른 숫자로 변경
평문과 암호문의 형식
기호의 조합으로 간주
정수로 표현
암호화 / 복호화 방식
C = Ek(P), P = Dk(C)
C = f(Kpub, P), P = g(Kpri, C)
활용 분야
길이가 긴 메세지 암호화
짧은 데이터 암호화, 전자 서명
알고리즘의 실행 시간
빠르다
늦다

φ(n)\varphi(n) : Euler의 φ\varphi함수

유명한 암호 알고리즘은 RSA알고리즘에서는 오일러의 φ\varphi함수를 알아야 알고리즘에 대한 이해가 가능하다. φ\varphi함수는 n보다 작으면서 n과 서로 소인 정수의 개수를 나타낸다.
ex) φ(10)\varphi(10) = count({1, 3, 7, 9}) = 4

φ(n)\varphi(n) 를 구하는 방법

•
φ(1)\varphi(1) = 0
•
φ(p)\varphi(p) = p - 1
p가 소수인 경우
•
φ(m∗n)=φ(m)∗φ(n)\varphi(m * n) = \varphi(m) * \varphi(n)
m과 n이 서로 소 일 때
•
φ(n)\varphi(n) = φ(pe)=pe−pe−1\varphi(p^e) = p^e - p^{e-1}
p가 소수일 때

φ(n)\varphi(n) 에 관한 오일러 정리

•
aφ(n)=1a^{\varphi(n)}=1
a와 n이 서로 소일 경우
•
ak∗φ(n)+1=a(mod(n))a^{k * \varphi(n)+1} = a (mod(n))
a < n, k가 정수이면

RSA 암호 시스템

Revest, Shamir, Adleman의 이름을 딴 공개 키 알고리즘으로 가장 널리 사용된다. 공개 키는 (e, n) 이고 개인 키는 d이다. 이 때 d는 수천 bit의 정수이다.
•
C=Pemod(n)C = P^e mod(n)
•
P=Cdmod(n)P = C^dmod(n)
해당알고리즘을 공격하려면 eCmod(n)^e\sqrt{C}mod(n) 을 계산해야 하는데, 현재까지 알려진 polynomial time 알고리즘은 없다. 따라서 공개키를 알아도 개인 키를 알아내는 것은 거의 불가능에 가깝다.

키 생성 알고리즘

RSA_Key_Generation { p != q 인 두 개의 큰 소수 p와 q를 선택한다. // p와 q는 각각 512bit 이상 n = p × q // n은 1024 비트 (309자리) 이상 φ(n) = (p − 1) × (q − 1) e = 1 < e < φ(n)이면서 φ(n)과 서로 소인 e를 선택한다. d = e^-1 mod φ(n) Public_key = (e, n) Private_key = d return Public_key and Private_key }
JavaScript
복사
이 때, e의 역원인 d를 구하기 위해서는 Extended Euclidian 알고리즘을 이용하여야 한다. 아래는 Extended Euclidian 알고리즘 파이썬 구현 코드이다. 자세한 설명은 따로 포스팅을 진행할 예정이다.
def extendedEuclidianAlgorithm(n, b): r1 = n; r2 = b t1 = 0; t2 = 1 while r2 > 0: q = math.floor(r1 / r2) r = r1 - q * r2 r1 = r2; r2 = r t = t1 - q * t2 t1 = t2 ; t2 = t if r1 != 1: raise Exception('역원이 없습니다') return t1
Python
복사

RSA의 정확성 증명

RSA가 안전하기 위한 권장 사항

•
n은 1024bit 이상 (4096bit 까지도 권고)
•
두 개의 소수 p와 q는 적어도 512bit 이상
•
p와 q는 너무 가까이 있는 수가 되지 않도록 설정
•
p - 1과 q - 1은 적어도 하나의 큰 소인수를 가져야 함
•
n 값을 공동으로 사용해서는 안된다.
•
e 값은 2162^{16} + 1 (=65537) 이거나 이 값에 가까운 정수를 사용
◦
e를 먼저 정한 후, e 와 φ(n)\varphi(n)이 서로 소가 되도록 p, q를 선택

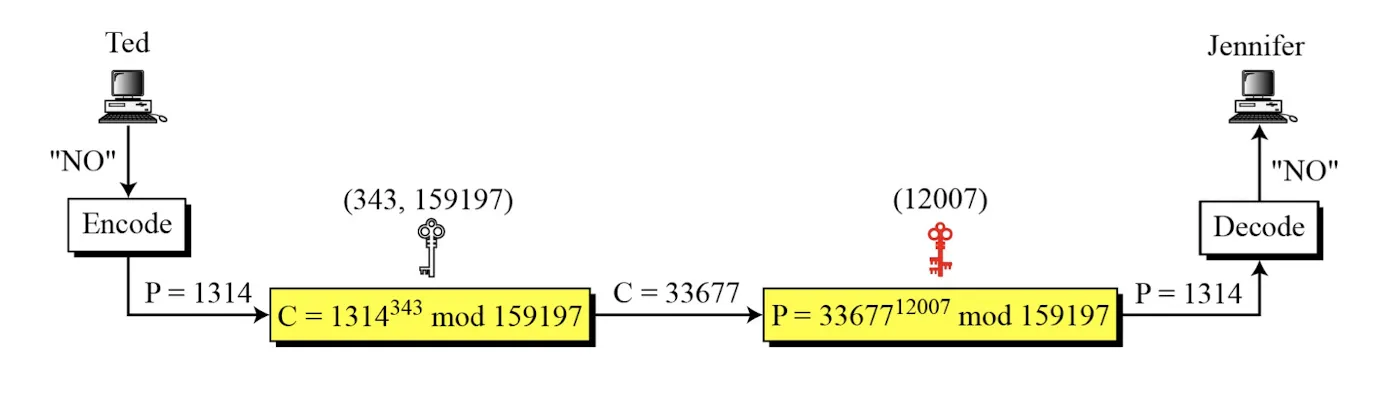
RSA의 간단한 예시

•
p = 397, q = 401
•
n = 159197 ( = p * q)
⇒ d = e−1mod(φ(n))e^{-1} mod(\varphi(n)) 인 e, d 선택
•
e = 343, d = 12007
1.
문자 “NO”를 숫자코드로 변경
2.
숫자코드를 이어서 하나의 숫자를 생성 ← 평문 P
3.
암호화, 복호화 진행

타원 곡선 암호 시스템

RSA는 보안을 위해서 키의 길이가 매우 커야 한다는 단점이 있다. n은 최소 1024bit 이상이여야 하며, 다른 값들을 포함하면, 키에 필요한 각종 정보들로 인해 패킷, 노드 등이 무거워 질 수 있다.
블록체인 시스템을 생각해보자. 블록체인에서는 각각의 노드들의 자격증명을 위해 보안 키를 들고있어야 하는데, 각 노드의 contents size보다 key의 크기가 더 커질 수 있다.
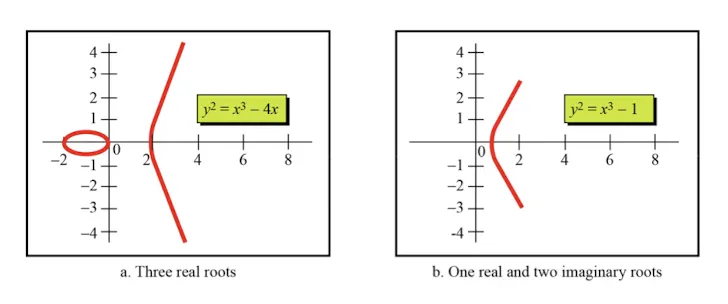
그래서 비트코인과 같은 블록체인 시스템에서는 타원 곡선 암호 시스템을 주로 사용한다. 키의 길이는 256bit 정도이지만, RSA와 동일한 수준의 보안을 제공한다. 타원 곡선 암호 시스템에서는 일반적인 타원 곡선 방정식이 아닌 실수 상의 타원 곡선을 사용한다. 아래의 식을 보자.
y2=x3+ax+by^2= x^3 + ax +b
이 곡선에서는 모든 근이 실근일 경우, 좌표의 수평선과 곡선이 3지점에서 교차한다.

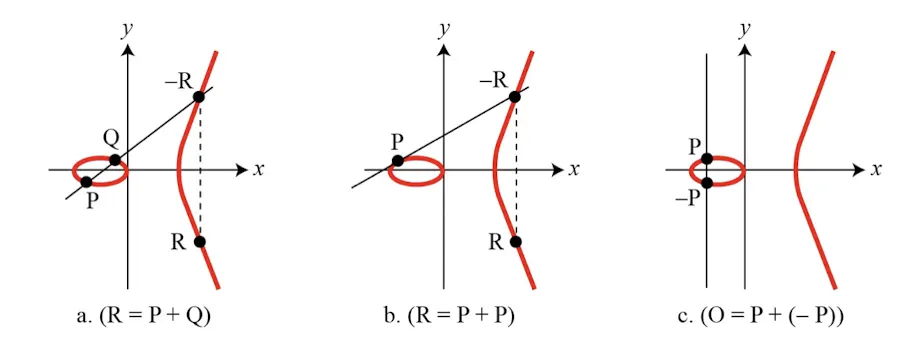
타원 곡성 상의 덧셈 연산

타원 곡선 상의 두 점 P, Q를 더하는 방법을 알아보자
•
P와 Q를 연결하는 직선과 교차하는 곡선상의 점 -R에 대해 x축으로 대칭한 점
•
P와 Q가 동일할 경우에는 P를 지나는 접선을 이용
•
a의 경우
λ=(y2−y1)/(x2−x1)\lambda = (y_2 - y_1) / (x_2 - x_1)
x3=λ2−x1−x2x_3 = \lambda^2 - x_1 - x_2
y3=λ(x1−x3)−y1y_3 = \lambda(x_1 - x_3) - y_1
•
b의 경우
λ=(3x12+a)/2y1\lambda = (3x_1^2 + a) / 2y_1
x3,y3x_3, y_3 은 위의 식과 동일

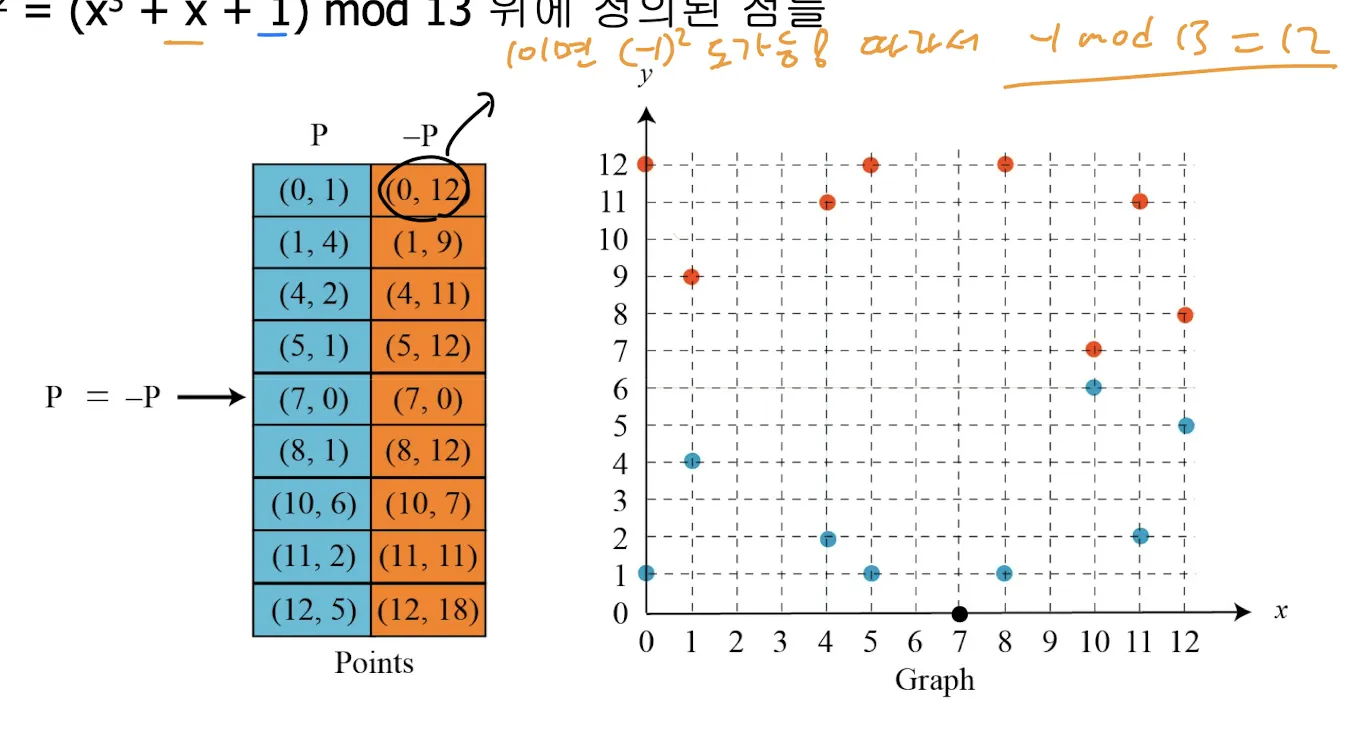
GF(p) 상의 타원 곡선

암호학에서는 무한 곡선을 사용하지 않는다. Modulo p를 이용해서 범위 내에 있는 점을 활용한다.
•
x의 값 : 0...p - 1
•
덧셈 연산 : 덧셈의 결과를 mod p
아래 예시를 보자

타원 곡선 E13(1,1)E_{13}(1,1)의 예

y2=(x3+x+1)mod13y^2 = (x^3 + x + 1) mod 13
위의 덧셈 연산을 활용해서 아래의 문제를 해결해보자
Ex) P = (4, 2), Q = (10, 6) 일 때, P + Q = R 이다. R의 좌표는?
풀이 및 해답

비트코인에서 사용하는 타원 곡선

비트 코인에서는 아래와 같은 타원 곡선 방정식을 사용한다. (Secp256k1)
y2=(x3+7)%py^2 = (x^3 + 7) \% p
여기서 사용하는 p는 아주 큰 소수이다.
p=2256−232−29−28−27−26−24−21p = 2^{256} - 2^{32} - 2^9 - 2^8 - 2^7 - 2^6 - 2^4 - 2^1
•
공개 키 K = k * G
◦
k : 개인 키(256bit)
◦
G : 타원 곡선 상의 고정된 점 → 이 점은 공개되어 있다.
공개 키로부터 개인 키를 유추하기 위해서는 적어도 k번의 덧셈이 필요하다. → 거의 불가능
마찬가지로 공개 키를 만들기 위해서도 연산이 필요하다. 하지만 Double-and-Add 알고리즘을 이용한다면, 어렵지 않게 공개 키를 생성할 수 있다.

Double-and-Add 알고리즘

•
left-to-right 로 k의 비트를 조사
•
1 : Double and Add
•
0 : Double
Made with