solved 난이도 보기
알고리즘 분류 보기
서론
과거에 알고리즘 공부를 하면서 오일러 회로에 대해서 공부 후 기본 문제에 대해서 구현을 하여 풀었던 문제입니다.
문제를 풀고 몇 달 뒤에 다시 보았을 때 데이터가 추가가 되면서 기존 답안이 시간 초과로 바뀌었습니다.
그 데이터 추가로 정답 비율이 바닥을 치게 되었고 이를 다시 해결하려고 구글링을 하여 힌트를 얻으려 했지만 당시에는 도저히 검색 결과가 나오질 않아서 스스로 고민 끝에 풀었던 기억이 있습니다.
이를 다시 복기 하면서 복습을 해보고자 다시 코드를 읽고 이 글을 작성하게 되었습니다.
시작
우선 이 문제를 해결하려면 오일러 회로에 대한 이론을 잘 알고 있어야합니다.
•
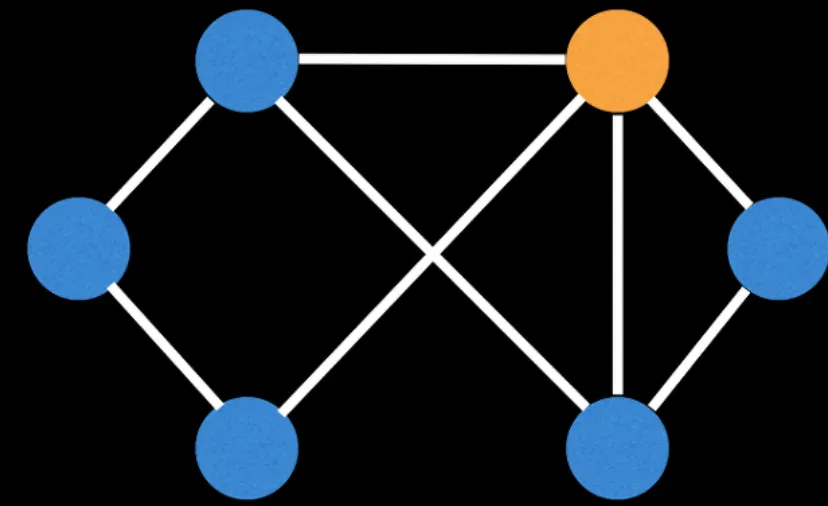
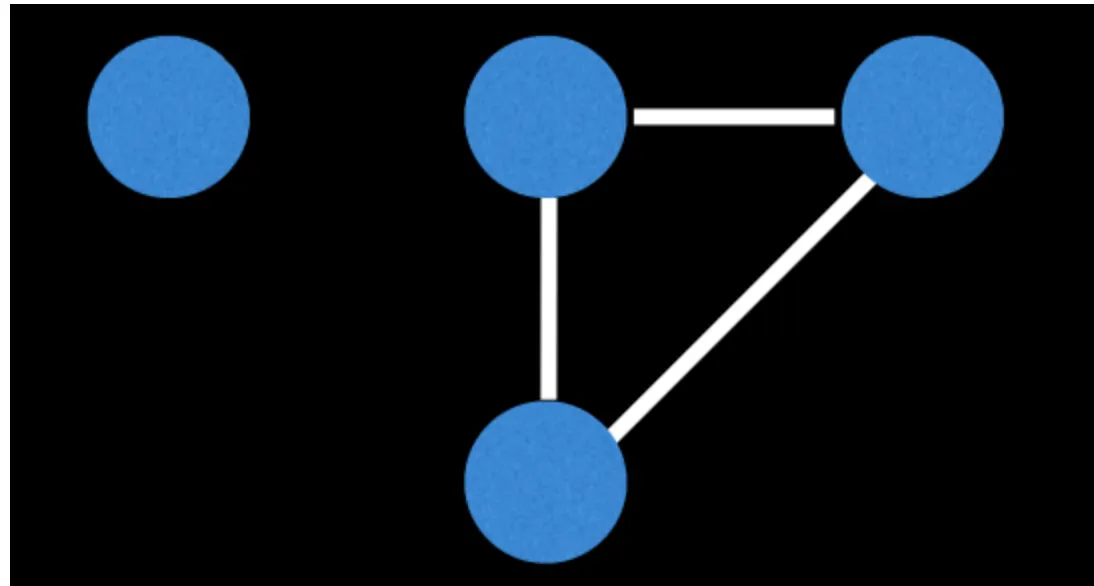
오일러 회로 vs 오일러 경로
기본적으로 둘 다 정점에 집중을 하는 것이 아닌 ‘간선’에 집중을 하는 문제입니다.
일반적으로 그래프에서 BFS,DFS 등으로 정점을 방문하고 visited 를 check 하는 것이 아닌
각 간선을 딱 한 번씩만 지나가고 모든 간선을 지날 수 있는지에 대해 확인하는 것입니다.
그게 가능한 경로가 오일러 경로이고 그 중에서 출발점과 도착점을 같은 경로를 오일러 회로라고 합니다.
오일러 경로
오일러 회로
주의해야 할 점이 간선이 단방향일 수도 있고 각 정점 사이에 하나 이상의 간선이 존재할 수 있다는 것입니다.
•
문제 설명
해당 문제는 N * N(1≤ N ≤ 1000) 인접 행렬이 주어지고 가능한 오일러 회로 아무거나 하나 출력하는 문제입니다.
스페셜 저지
1.
양방향 간선
2.
각 정점 사이에 여러 개의 간선 존재 가능 (최대 10개까지)
3.
자기 자신으로의 간선은 없음
4.
모든 정점은 연결되어 있음
이 경우에는 고려해야 하는 예외 경우가 생성되는데 이를 배제해도 됨.
구현
우선 오일러 회로가 존재하는지 안하는지 조건을 확인하고 존재하지 않는다면 -1을 출력하도록 예외처리를 하여 불가능한 경우를 빠르게 찾아낼 수 있다.
1.
그래프의 모든 노드는 연결되어 있어야 한다. → 위에 조건 4번으로 고려하지 않아도 됨
2.
그래프의 모든 노드의 차수는 짝수여야 한다.
→ 각 노드는 들어오는 간선이 있으면 그 개수에 맞게 나가는 간선이 있어야 해당 노드에서 더 이상 진행하지 않는 경우가 안생긴다.
→ 시작점의 경우에는 나가는 간선이 있으면 반드시 다시 들어오는 간선이 있어야 한다.
주의 . 위 조건은 양뱡향 간선일 경우에 필요한 조건이다.
cin >> n;
adj = vector<vector<int>>(n, vector<int>(n, 0));
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
cin >> adj[i][j];
}
}
C++
복사
기본적으로 N*N 인접행렬을 만듭니다.
adj[a][b] : a에서 b로의 간선의 개수
for (int i = 0; i < n; i++) {
int sum = 0;
for (int j = 0; j < n; j++) {
if (adj[i][j] > 0) {
sum += adj[i][j];
}
}
if (sum % 2 == 1) {
cout << -1 << '\n';
return 0;
}
}
C++
복사
i 노드와 연결되어 있는 모든 간선의 개수를 sum에 더해서 위의 2번 조건에 부합하는지 확인
vector<int> ans;
void getEulerCircuit(int here)
{
for (int i = 0; i < n; i++) {
if (adj[here][i] > 0) {
adj[here][i]--;
adj[i][here]--;
getEulerCircuit(i);
}
}
ans.push_back(here);
}
C++
복사
ans를 전역변수로 생성하여 getEulerCircuit함수를 DFS 형식으로 재귀함수를 통해 돌려 줍니다.
첫 함수에는 시작하는 정점의 번호를 넣어주면 되는데 어디서 출발하든 상관이 없습니다.
해당 함수에서는 here 정점에서 도착할 수 있는 모든 정점을 방문 후에 간선의 개수를 하나씩 줄이면서 간선을 없애 나갑니다.
그 후 백트래킹 과정에서 ans에 현재 경로를 추가하여 ans에는 방문 순서가 역순으로 삽입되게 됩니다.
dfs를 통해 모든 간선을 지나친 후 종료되면 ans를 역순으로 출력해주면 답이 됩니다.
(사실 역순으로 출력하지 않아도 그 또한 오일러회로이므로 그대로 출력해줘도 상관이 없습니다.)
결론
이것이 기본적인 오일러 회로의 구현 방법입니다.
이렇게 코드를 작성하면 오일러 회로를 문제없이 잘 출력하지만 해당 백준 문제에서는 시간초과가 일어나게 됩니다.
만약 최고의 시간복잡도를 갖게 되는 1000 * 1000 행렬에 모든 간선이 10개씩 있게 된다면 getEulerCircuit함수를 들어가게 되면
매번 1000개에 해당하는 노드를 체크하여 간선이 존재하는지 확인하고 그것을 10번씩 해야한다. 어마어마한 시간복잡도를 갖게 될 것입니다.
대략적으로 1000 * 1000 * 10 * 1000 의 계산이 필요할 것으로 추정됩니다.
데이터 추가가 없었을 때는 이 코드로 충분히 통과하였지만 데이터가 추가된 이후로 이렇게 하면 무조건 시간초과를 맛보게 됩니다.
이를 해결하기 위해 코드를 어떻게 수정했는지에 대해서는 다음 게시글에서 작성하겠습니다.
잘못된 내용이나 부족한 내용 지적해주시면 감사하겠습니다!