복잡도
복잡도는 계산 복잡도를 의미합니다. 이 계산 복잡도를 활용하면 당신이 설계한 알고리즘을 실제로 프로그래밍한 뒤 실행하기 전에 대략적으로 얼마만큼의 계산을 요구하며 얼마만큼의 메모리 공간을 요구하는지를 알 수 있습니다. 그리고 계산 복잡도는 시간 복잡도와 공간 복잡도로 나눌 수 있습니다. 이번 글에서는 시간 복잡도에 대해 다루겠습니다.
빅오 표기법
#include <iostream>
using namespace std;
int main()
{
int N;
cin >> N;
int count = 0;
for (int i = 0; i < N; i++)
{
count++;
}
return 0;
}
Plain Text
복사
시간 복잡도를 이야기하기 위해 빅오 표기법을 사용합니다. 위 코드에서 N이 10배 증가하면 이에 따라 비례로 계산 시간은 10배 증가합니다. 이를 복잡도 O(N)이라고 표기합니다. 이 표기법은 란다우 O 표기법 또는 빅오 표기법이라고 합니다.
위 코드의 복잡도
•
int i 선언을 1번
•
조건 판단을 N + 1번
•
i++를 N + 1번
•
count++를 N번
for 문 안에서 총 3N + 2번의 계산이 요구됩니다. 결국 대략적으로 N에 비례하는걸 알 수 있습니다. 그리고 N이 충분히 커지면 '+2'는 무시해도 무방합니다.
실제 복잡도 구하기
어떤 알고리즘 계산 시간 T(N)이 다음과 같다면 T(N) = 3N^2 + 5N + 100 복잡도를 어떻게 나타내면 좋을까요? 그냥 있는 그대로 이 알고리즘은 크기 N 입력에 대해 3N^2 + 5N + 100의 계산 시간이 필요하다라고 구체적으로 서술하는 것도 방법입니다. 하지만 대입이나 초기화 같은 작업 실행 시간은 컴퓨터 환경, 프로그래밍 언어, 컴파일러 종류 등에 따라 실제로 걸리는 시간이 달라집니다. 따라서 이런 부분에 좌우되지 않고 알고리즘을 계산하는 데 걸리는 시간을 논의하려면 정수배나 낮은 차수의 항의 영향을 받이 않아야 합니다. 이때 란다우 O 표기법이 편리합니다.
란다우 표기법에 의해 3N^2 + 5N + 100 을 N^2으로 나누어주고 극한으로 보냅니다. 결과는 3입니다. 이렇게 되면 T(N)은 대략 N^2에 비례한다고 생각할 수 있습니다. 이걸 T(N) = O(N^2)라고 나타내고 이 알고리즘 복잡도는 O(N^2)라고 부릅니다. 실제로는 다음과 같은 절차로 복잡도를 구합니다.
1.
3N^2 + 5N + 100에서 최고차항 이외는 버리고 3N^2로 함
2.
3N^2 에서 계수를 무시하고 N^2라고 함
복잡도를 구하는 예: 짝수 나열
#include <iostream>
using namespace std;
int main()
{
int N;
cin >> N;
for (int i = =2; i < N; i += 2)
{
cout << i << '\n';
}
return 0;
}
Plain Text
복사
이 알고리즘의 for문 반복 횟수는 N/2회다. 따라서 계산 시간은 대략 N에 비례하므로 O(N)이 됩니다.
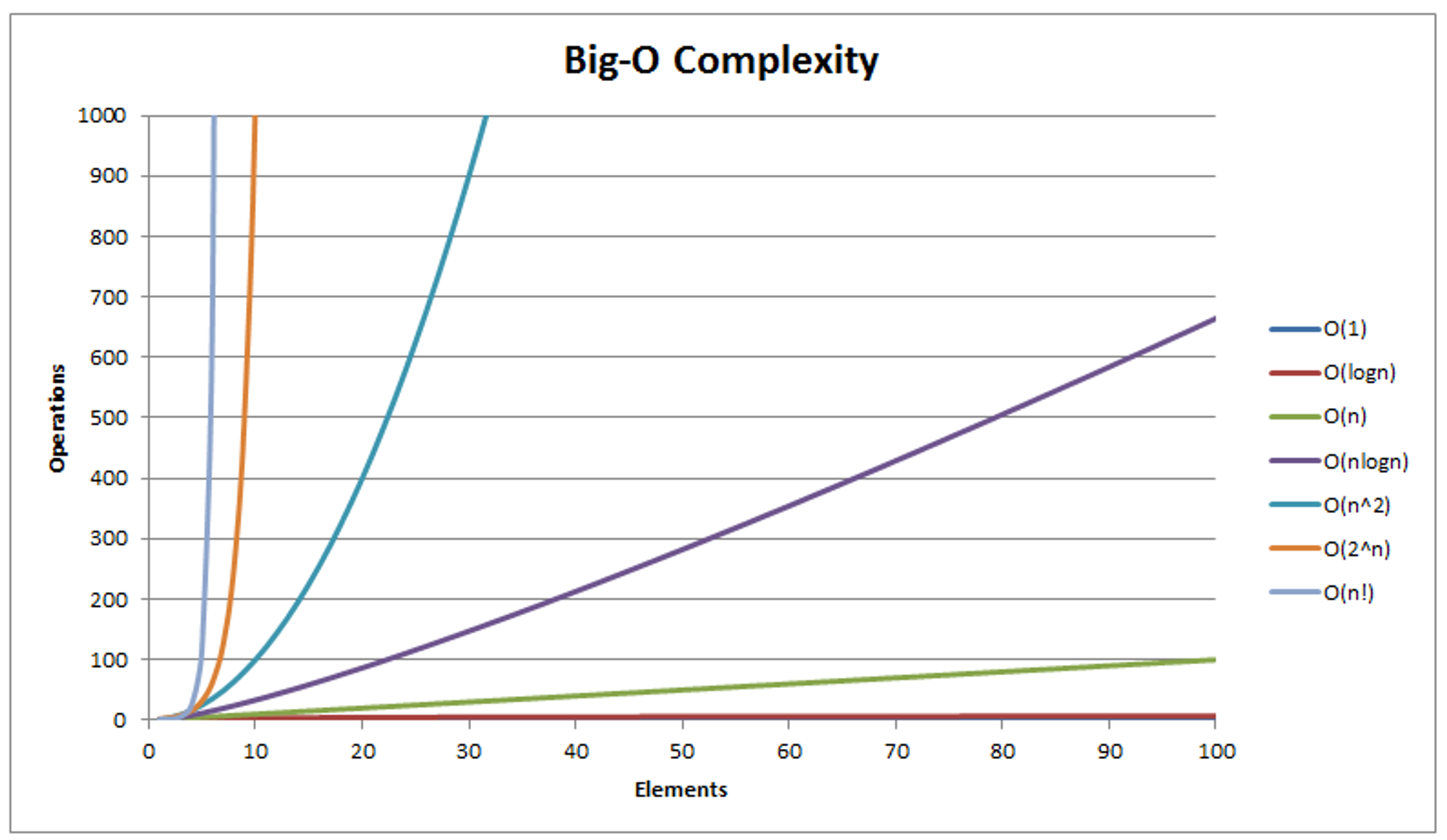
복잡도 비교
복잡도 관련 주의 사항
시간 복잡도와 공간 복잡도
지금까지 논의한 복잡도는 모두 알고리즘 계산 시간에 대한 것입니다. 이 부분을 강조하고 싶을 때는 시간 복잡도라고 부릅니다. 반면 알고리즘을 실행할 때 사용하는 메모리 사용량을 가리키는 공간 복잡도라는 개념도 알고리즘의 좋고 나쁨을 측정하는 척도로 자주 사용합니다.
최악 시간 복잡도와 평균 시간 복잡도
알고리즘 실행 시간은 입력 데이터가 나열되어 있는 방식의 편차에 따라 빠를 수도, 느릴 수도 있습니다. 최악의 경우에 해당하는 시간 복잡도를 최악 시간 복잡도라고 합니다. 평균적인 경우에 해당되는 시간 복잡도를 평균 시간 복잡도라고 합니다. 정확하게 말하자면, 평균 시간 복잡도는 입력 데이터 분포 상태가 이러하다고 가정한 경우의 시간 복잡도 기댓값입니다.