Search
Duplicate
🥕

Jacobsthal 수열의 일반항 유도

간단소개
팔만코딩경 컨트리뷰터
ContributorNotionAccount
주제 / 분류
Algorithm
Scrap
태그
9 more properties

개요

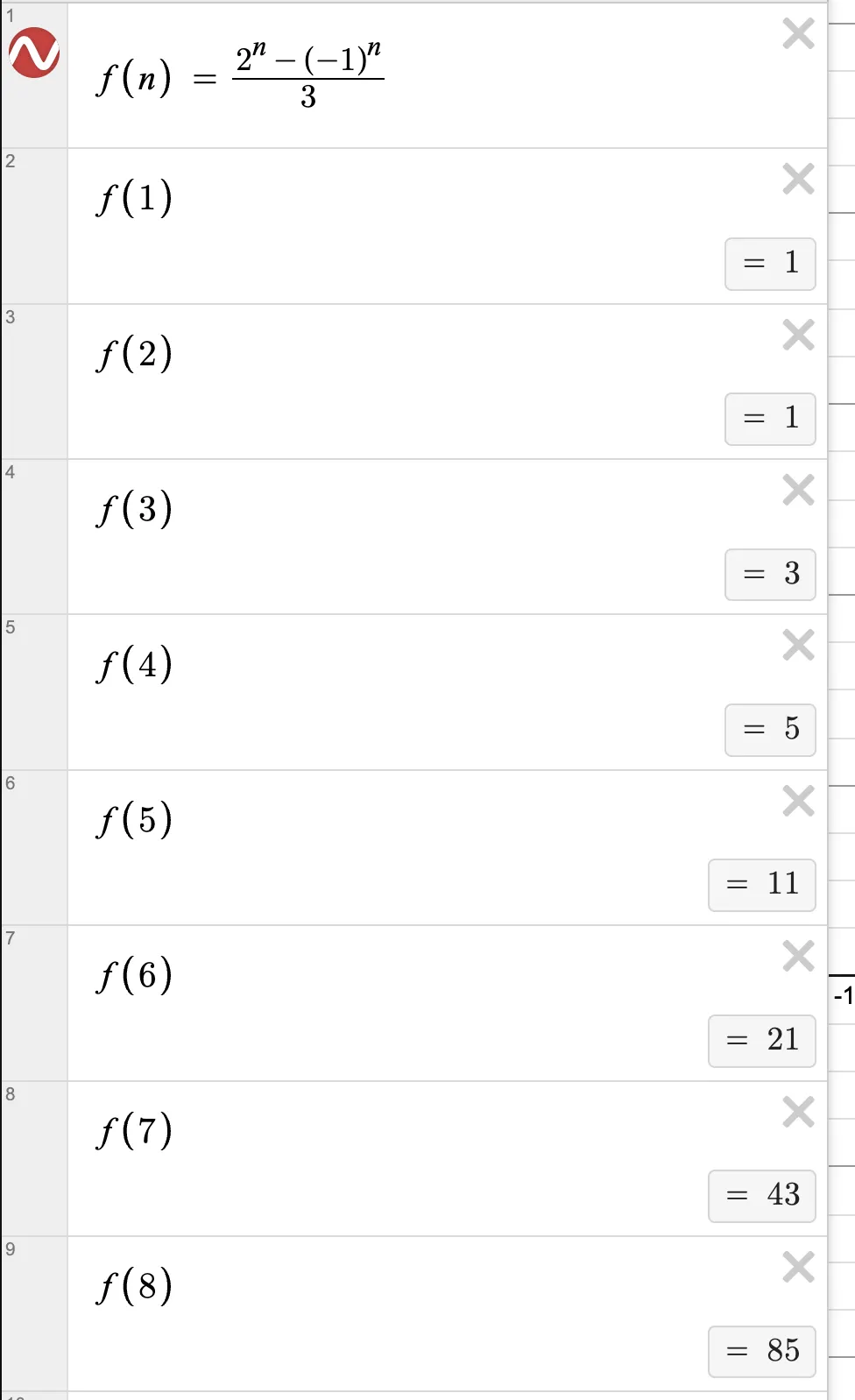
Merge-insertion sort 라는 정렬 알고리즘을 찾아보려고 원본 논문을 봤는데, (or 포드존슨 Ford-Johnson) 알고리즘에서 사용되는 수열에 대한 closed form 식을 설명없이 적어만 놨다...(빨간색으로 표시한 부분) 일단 수열의 명칭이 원문에서 언급되진 않았으나 동일한 형태의 수열이 Jacobsthal sequence라는 이름으로 존재한다. 그래서 이 수열을 직접 점화식에서부터 유도해보려고 한다. 수열의 점화식은 아래와 같다.
a0=0a_0 = 0 a1=1a_1 = 1 an=an−1+2an−2(n≥2)a_n = a_{n-1} + 2a_{n-2} \quad (n \geq 2)
{0,1,1,3,5,11,21,43,...}\{ 0, 1, 1, 3, 5, 11, 21, 43, ... \} 피보나치 수열 {an=an−1+an−2}\{ a_n = a_{n-1} + a_{n-2} \} 과 비슷한 형태. 이 점화식을 가지고 closed form을 유도해볼 건데, 방법은 이것저것 있으나 생성함수로 일단 유도해보자. (사실 Characteristic equation을 사용하면 쉽게 풀 수 있지만, 배운다는 생각으로…)

Generating function

일단 생성함수가 무엇인지 설명하자면, 일단 수열이나 경우의 수 등의 각 항을 계수로 하는 다항식을 생각하는 것이다. 예를 들어, 1~6까지 적힌 주사위를 던져서 나올 수 있는 경우의 수를 식으로 나타내려면 이렇게 나타낼 수 있다. 1x+1x2+1x3+1x4+1x5+1x61x + 1x^2 + 1x^3 + 1x^4 + 1x^5 + 1x^6
각 지수는 주사위의 눈을 나타내고, 각 계수는 그 눈이 나올 경우의 수를 나타낸다. 생성함수는 이렇게 각 항을 계수로 하는 다항식을 생각하는 것이다. 수열도 마찬가지로 각 항을 계수로 생성함수를 정의할 수 있다. G(x)=0+1x+1x2+3x3+5x4+11x5+...G(x) = 0 + 1x + 1x^2 + 3x^3 + 5x^4 + 11x^5 + ... 여기서 특정 지수의 계수를 골라낼 수 있다면, 곧바로 수열의 n번째 항을 구할 수 있을 것이다. 일단 Jacobsthal sequence의 생성함수 G(x)G(x)를 다음과 같이 정의하자. G(x)=a0+a1x+a2x2+a3x3+...=∑n=0∞anxnG(x) = a_0 + a_1x + a_2x^2 + a_3x^3 + ... = \sum\limits_{n=0}^{\infty} a_nx^n 이걸 기존 점화식의 양 변에 xnx^n을 곱하고 생성함수에 맞게 ∑n=0∞anxn\sum\limits_{n=0}^{\infty} a_nx^n으로 정리하면,
an=an−1+2an−2anxn=an−1xn+2an−2xn∑n=2∞anxn=∑n=2∞an−1xn+2∑n=2∞an−2xn∑n=0∞[anxn]−a0−a1x=x∑n=2∞[an−1xn−1]+2x2∑n=2∞[an−2xn−2]∑n=0∞[anxn]−x=x∑n=0∞[anxn]+2x2∑n=0∞[anxn]G(x)−x=xG(x)+2x2G(x)G(x)−xG(x)−2x2G(x)=xG(x)(1−x−2x2)=xG(x)=x1−x−2x2\begin{aligned} a_n & = a_{n-1} + 2a_{n-2} \\ a_nx^n & = a_{n-1}x^n + 2a_{n-2}x^n \\ \sum\limits_{n=2}^{\infty} a_nx^n & = \sum\limits_{n=2}^{\infty} a_{n-1}x^n + 2\sum\limits_{n=2}^{\infty} a_{n-2}x^n \\ \sum\limits_{n=0}^{\infty} [a_nx^n] - a_0 - a_1x & = x \sum\limits_{n=2}^{\infty} [a_{n-1}x^{n-1}] + 2x^2 \sum\limits_{n=2}^{\infty} [a_{n-2}x^{n-2}] \\ \sum\limits_{n=0}^{\infty} [a_nx^n] - x & = x \sum\limits_{n=0}^{\infty} [a_{n}x^{n}] + 2x^2 \sum\limits_{n=0}^{\infty} [a_{n}x^{n}] \\ G(x) - x & = xG(x) + 2x^2G(x) \\ G(x) - xG(x) - 2x^2G(x) & = x \\ G(x)(1 - x - 2x^2) & = x \\ G(x) & = \frac{x}{1 - x - 2x^2} \end{aligned}
이렇게 수열의 생성함수를 xx에 대하여 구할 수 있는데, 우리가 원하는 nn번째 수열의 항을 구하기 위해선 여기서 xnx^n의 계수 걸러내야 한다. 이를 위해 부분분수분해 를 사용할 것이다. 부분분수분해는 통분된 분수를 다른 분수로 분해하는 방법인데,
P(x)Q(x)=c0x−r0+c1x−r1+...+cnx−rn \frac{P(x)}{Q(x)} = \frac{c_0}{x - r_0} + \frac{c_1}{x - r_1} + ... + \frac{c_n}{x - r_n}
P(x)P(x)와 Q(x)Q(x)가 xx에 대한 다항식이고, Q(x)Q(x)가 (x−a0)(x−a1)⋅⋅⋅(x−an)(x - a_0)(x - a_1) \cdot\cdot\cdot (x - a_n)의 형태라면 위와 같이 분해할 수 있다. c0,c1,...cnc_0, c_1, ... c_n은 임의의 상수. x1−x−2x2\frac{x}{1 - x - 2x^2} 는 분모와 분자가 xx에 대한 다항식이므로 위의 형태로 분해할 수 있다. 일단 xx의 해를 구하면
1−x−2x2=01 - x - 2x^2 = 0
x=−1±1+8−4=−1±3−4=12 or−1\begin{aligned} x & = \frac{-1 \pm \sqrt{1 + 8}}{-4} = \frac{-1 \pm 3}{-4} \\ & = \frac{1}{2} \ or -1 \end{aligned}
x=12 or−1x = \frac{1}{2} \ or -1 이므로 부분분수분해 형태로 나타내도록 하자.
G(x)=x1−x−2x2=x(x−12)(x+1)=x(1−2x)(1−(−x)) \begin {aligned} G(x) & = \frac{x}{1 - x - 2x^2} \\ & = \frac{x}{(x - \frac{1}{2})(x + 1)} \\ & = \frac{x}{(1 - 2x)(1 - (-x))} \\ \end{aligned}
x(1−2x)(1−(−x))=A1−2x+B1−(−x)x=A(1−(−x))+B(1−2x)A=13when x=−1B=−13when x=12\begin{aligned} \frac{x}{(1 - 2x)(1 - (-x))} & = \frac{A}{1 - 2x} + \frac{B}{1 - (-x)} \\ x & = A(1 - (-x)) + B(1 - 2x) \\ \\ A = \frac{1}{3} & \quad when \ x = -1 \\ B = -\frac{1}{3} & \quad when \ x = \frac{1}{2} \\ \end{aligned}
후에 무한등비급수를 사용할 것이므로 (1−x)(1 - x) 형태로 정리했다. 이제 G(x)G(x)의 부분분수분해 식에 위에서 구한 A,BA, B를 대입해보자.
G(x)=13⋅11−2x−13⋅11−(−x) \begin{aligned} G(x) & = \frac{1}{3} \cdot \frac{1}{1 - 2x} - \frac{1}{3} \cdot \frac{1}{1 - (-x)} \end{aligned}
여기서 11−x\frac{1}{1 - x}의 형태는 무한등비급수를 사용할 수 있다.
11−x=∑n=0∞xn\frac{1}{1-x} = \sum\limits_{n=0}^{\infty} x^n 원래 ∥x∥<1{\|x\|} < 1일 때만 성립하는데, 우리가 사용하는 생성함수는 formal power series이므로 coverage를 무시해도 된다.
G(x)=13⋅11−2x−13⋅11−(−x)=13∑n=0∞(2x)n−13∑n=0∞(−x)n=∑n=0∞13⋅2n⋅xn−∑n=0∞13⋅(−1)n⋅xn=∑n=0∞[2n−(−1)n3]⋅xn \begin{aligned} G(x) & = \frac{1}{3} \cdot \frac{1}{1 - 2x} - \frac{1}{3} \cdot \frac{1}{1 - (-x)} \\ & = \frac{1}{3} \sum\limits_{n=0}^{\infty} (2x)^n - \frac{1}{3} \sum\limits_{n=0}^{\infty} (-x)^n \\ & = \sum\limits_{n=0}^{\infty} \frac{1}{3} \cdot 2^n \cdot x^n - \sum\limits_{n=0}^{\infty} \frac{1}{3} \cdot (-1)^n \cdot x^n \\ & = \sum\limits_{n=0}^{\infty} [\frac{2^n - (-1)^n}{3}] \cdot x^n \\ \end{aligned}
우리는 nn번 항의 계수를 구하는 것이 목적이므로 xnx^n는 필요없음.
an=2n−(−1)n3 a_n = \frac{2^n - (-1)^n}{3}
최종적으로 구한 Jacobsthal sequence의 closed form 식은 위와 같다.
잘 유도됐음

Characteristic equation

Charaacteristic equation을 사용하여 유도하는 방법은 다음과 같은데,
an=an−1+2an−2a_n = a_{n-1} + 2a_{n-2}
야콥스탈 수열의 경우 상수계수를 가지는 점화식으로 만들어지므로 수열이 지수적으로 증가한다.
rn=rn−1+2rn−2r^n = r^{n-1} + 2r^{n-2}
그러므로 ana_n을 rnr^n으로 가정해볼 수 있다. (정수여서 가능)
rn−2r^{n-2}로 나눠서 정리. r2=r+2r^2 = r + 2
r2−r−2=0r^2 - r - 2 = 0
r=1±1+82=2 or −1r = \frac{1 \pm \sqrt{1 + 8}}{2} = 2 \ or \ -1
그러므로 ana_n은 2 와 -1의 거듭제곱에 대한 선형결합으로 이루어진다고 볼 수 있다.
an=c0⋅2n+c1⋅(−1)na0=0=c0+c1c0=−c1a1=1=2c0−c1c0=13c1=−13\begin{aligned} a_n & = c_0\cdot2^n + c_1\cdot(-1)^n \\ \\ a_0 & = 0 = c_0 + c_1 \\ c_0 & = -c_1 \\ \\ a_1 & = 1 = 2c_0 - c_1 \\ \\ c_0 & = \frac{1}{3} \\ c_1 & = -\frac{1}{3} \end{aligned}
최종적으로 ana_n은 다음과 같다.
an=2n−(−1)n3a_n = \frac{2^n - (-1)^n}{3}
결국 c0,c1c_0, c_1이 생성함수 유도에서의 A,BA, B에 해당하는 녀석들이라는걸 알 수 있다. 근본적인 풀이 원리는 같다.

Eigenbasis

수열의 점화식은 선형변환의 형태를 가지므로 이를 행렬로 나타낼 수 있다.
an=an−1+2an−2 a_n = a_{n-1} + 2a_{n-2} \\
[anan−1]=[1210][an−1an−2] \begin{aligned} \begin{bmatrix} a_n \\ a_{n-1} \end{bmatrix} & = \begin{bmatrix} 1 & 2 \\ 1 & 0 \end{bmatrix} \begin{bmatrix} a_{n-1} \\ a_{n-2} \end{bmatrix} \end{aligned}
ana_n은 [an−1an−2]\begin{bmatrix} a_{n-1} \\ a_{n-2} \end{bmatrix}를 [1210]\begin{bmatrix} 1 & 2 \\ 1 & 0 \end{bmatrix}로 선형변환한 결과이다. 그러므로 ana_n은 시작점 [10]=[a1a0]\begin{bmatrix} 1 \\ 0 \end{bmatrix} = \begin{bmatrix} a_1 \\ a_0 \end{bmatrix} 을 n-1번 선형변환한 결과라고 볼 수 있으므로, 다음과 같이 제곱을 이용하여 표현할 수 있다.
[anan−1]=[1210]n−1[10] \begin{aligned} \begin{bmatrix} a_n \\ a_{n-1} \end{bmatrix} & = \begin{bmatrix} 1 & 2 \\ 1 & 0 \end{bmatrix}^{n-1} \begin{bmatrix} 1 \\ 0 \end{bmatrix} \end{aligned}
여기서 문제가 있는데, [1210]\begin{bmatrix} 1 & 2 \\ 1 & 0 \end{bmatrix} 의 제곱은 계산하기 쉽지 않다. (다른 원소에 영향을 미치기 때문) 하지만 [x00y]\begin{bmatrix} x & 0 \\ 0 & y \end{bmatrix}같은 꼴의 행렬의 제곱은 간단하게 [xn00yn]\begin{bmatrix} x^n & 0 \\ 0 & y^n \end{bmatrix}로 나타낼 수 있는데, 이 특성을 적용시키기 위해 선형변환 [1210]\begin{bmatrix} 1 & 2 \\ 1 & 0 \end{bmatrix} 에 대해 회전 영향을 받지 않는 두 벡터를 찾은 뒤 이를 축(basis)으로 하는 좌표계로 변환하여 선형변환을 적용시키면 간단하게 제곱을 구할 수 있을 것이다. 이러한 벡터를 eigenvector라고 하며, 회전엔 영향을 받진 않으나 스케일에 영향을 받을 수 있으므로 이 스케일 값을 eigenvalue라고 한다. 그러면 다음 행렬변환 [1210]\begin{bmatrix} 1 & 2 \\ 1 & 0 \end{bmatrix} 의 영향을 받지 않는 벡터를 찾아보자. [1210]\begin{bmatrix} 1 & 2 \\ 1 & 0 \end{bmatrix} 를 회전변환 TT라고 하고, 이를 식으로 표현하면 다음과 같다.
Tv⃗=λv⃗( where v⃗ is eigenvector and λ is eigenvalue) \begin{aligned} T\vec{v} & = \lambda\vec{v} \quad (\text{ where } \vec{v} \text{ is eigenvector and } \lambda \text{ is eigenvalue}) \end{aligned}
우리는 v⃗\vec{v}을 원하므로 v⃗\vec{v}에 대해 풀어보자.
Tv⃗=λv⃗Tv⃗−λv⃗=0⃗(T−λI)v⃗=0⃗v⃗=(T−λI)−10⃗ \begin{aligned} T\vec{v} & = \lambda\vec{v} \\ T\vec{v} - \lambda\vec{v} & = \vec{0} \\ (T - \lambda I)\vec{v} & = \vec{0} \\ \vec{v} & = (T - \lambda I)^{-1}\vec{0} \\ \end{aligned}
그런데 우변은 0⃗\vec{0}이므로 어떠한 행렬변환의 결과도 0⃗\vec{0}이고 v⃗\vec{v}는 영벡터가 될 것이다. 우리는 축으로 사용할 벡터가 필요하므로 영벡터는 사용할 수 없으니 v⃗\vec{v}는 영벡터가 아니어야 한다. 그러므로 (T−λI)(T - \lambda I)의 역행렬이 존재하지 않는 경우에만 영벡터가 아닌 v⃗\vec{v}를 찾을 수 있다.
역행렬이 존재하기 위해선 det⁡(T−λI)=0\det(T - \lambda I) = 0이 아니어야 한다. 왜냐하면 det⁡(a⃗)\det(\vec{a})가 0이라는 것은 한 축의 정보가 소실되어 차원이 축소되었다는 것을 의미하기 때문에, 선형변환 이전의 벡터로 되돌릴 수 없다. 우리는 det⁡(T−λI)=0\det(T - \lambda I) = 0을 만족하는 λ\lambda를 찾아야 한다.
det⁡(T−λI)=0det⁡([1210]−[λ00λ])=0det⁡[1−λ21−λ]=0(1−λ)(−λ)−2=0λ2−λ−2=0λ=1±1+82λ=2 or −1 \begin{aligned} \det(T - \lambda I) & = 0 \\ \det(\begin{bmatrix} 1 & 2 \\ 1 & 0 \end{bmatrix} - \begin{bmatrix} \lambda & 0 \\ 0 & \lambda \end{bmatrix}) & = 0 \\ \det\begin{bmatrix} 1 - \lambda & 2 \\ 1 & -\lambda \end{bmatrix} & = 0 \\ (1 - \lambda)(-\lambda) - 2 & = 0 \\ \lambda^2 - \lambda - 2 & = 0 \\ \lambda & = \frac{1 \pm \sqrt{1 + 8}}{2} \\ \lambda & = 2 \ or \ -1 \end{aligned}
이렇게 λ\lambda를 찾았다.
그런데 뭔가 이상하지 않은가? 이전 풀이에서 나왔던 주요 값인 2와 -1이 또 여기서 나왔다.
사실 Characteristic equation은 선형대수의 해당 eigenvalue를 다루는 개념이고 선형변환은 고유한 어떤 값이 존재한다는것을 이용하는 것이다.
어쨋든 이제 λ\lambda를 대입해서 만족하는 v⃗\vec{v}들을 찾아보자.
(T−λI)v⃗=0⃗[1−λ21−λ]v⃗=0⃗if λ=2, [−121−2]v⃗=0⃗v1−2v2=0v1=2v2v⃗=[21]if λ=−1, [2211]v⃗=0⃗2v1+2v2=0v1+v2=0v1=−v2v⃗=[1−1] \begin{aligned} (T - \lambda I)\vec{v} & = \vec{0} \\ \begin{bmatrix} 1 - \lambda & 2 \\ 1 & -\lambda \end{bmatrix}\vec{v} & = \vec{0} \\ if \ \lambda = 2, \ \begin{bmatrix} -1 & 2 \\ 1 & -2 \end{bmatrix}\vec{v} & = \vec{0} \\ v_1 - 2v_2 & = 0 \\ v_1 & = 2v_2 \\ \vec{v} & = \begin{bmatrix} 2 \\ 1 \end{bmatrix} \\ \\ if \ \lambda = -1, \ \begin{bmatrix} 2 & 2 \\ 1 & 1 \end{bmatrix}\vec{v} & = \vec{0} \\ 2v_1 + 2v_2 & = 0 \\ v_1 + v_2 & = 0 \\ v_1 & = -v_2 \\ \vec{v} & = \begin{bmatrix} 1 \\ -1 \end{bmatrix} \\ \end{aligned}
이 벡터 2개를 열벡터로 하는 행렬을 새로운 좌표계 BB로 사용하여 선형연산을 이 좌표계에서 수행할 것이다.
기존 선형변환 TT는 좌표계변환 → T^\hat{T}변환 → 좌표계복구 로 치환.
B=[211−1]\begin{aligned} B = \begin{bmatrix} 2 & 1 \\ 1 & -1 \end{bmatrix} \end{aligned}
T=BT^B−1B−1TB=T^ \begin{aligned} T & = B\hat{T}B^{-1} \\ B^{-1}TB & = \hat{T} \\ \end{aligned}
이제 T^\hat{T}를 구하면 이를 제곱하여 ana_n을 구할 수 있다
T^=B−1TBT^=B−1TB=[211−1]−1[1210][211−1]T^=B−1TB=[131313−23][1210][211−1]T^=B−1TB=[200−1]T=BT^B−1=[211−1][200−1][131313−23]Tn−1=[211−1][2n−100(−1)n−1][131313−23]\begin{aligned} \hat{T} & = B^{-1}TB \\ \hat{T} & = B^{-1}TB = \begin{bmatrix} 2 & 1 \\ 1 & -1 \end{bmatrix}^{-1}\begin{bmatrix} 1 & 2 \\ 1 & 0 \end{bmatrix}\begin{bmatrix} 2 & 1 \\ 1 & -1 \end{bmatrix} \\ \hat{T} & = B^{-1}TB = \begin{bmatrix} \frac{1}{3} & \frac{1}{3} \\ \frac{1}{3} & -\frac{2}{3} \end{bmatrix}\begin{bmatrix} 1 & 2 \\ 1 & 0 \end{bmatrix}\begin{bmatrix} 2 & 1 \\ 1 & -1 \end{bmatrix} \\ \hat{T} & = B^{-1}TB = \begin{bmatrix} 2 & 0 \\ 0 & -1 \end{bmatrix} \\ T = B\hat{T}B^{-1} & = \begin{bmatrix} 2 & 1 \\ 1 & -1 \end{bmatrix}\begin{bmatrix} 2 & 0 \\ 0 & -1 \end{bmatrix}\begin{bmatrix} \frac{1}{3} & \frac{1}{3} \\ \frac{1}{3} & -\frac{2}{3} \end{bmatrix} \\ T^{n-1} & = \begin{bmatrix} 2 & 1 \\ 1 & -1 \end{bmatrix}\begin{bmatrix} 2^{n-1} & 0 \\ 0 & (-1)^{n-1} \end{bmatrix}\begin{bmatrix} \frac{1}{3} & \frac{1}{3} \\ \frac{1}{3} & -\frac{2}{3} \end{bmatrix} \\ \end{aligned}
그런데 사실 T^\hat{T}를 직접 구할 필요는 없다. 왜냐하면 선형변환 TT와 그 고유값 λd\lambda^d로 이루어진 대각행렬의 선형변환은, Aigenvector로 이루어진 aigenbasis BB 좌표계에서 동일한 선형변환이기 때문이다. 그래서 구해진 T^\hat{T}가 우리가 구한 λ0,λ1=2,−1\lambda_0, \lambda_1 = 2, -1 을 원소로 하는 대각행렬인 것이다.
T^=[200−1]=[λ000λ1]\hat{T} = \begin{bmatrix} 2 & 0 \\ 0 & -1 \end{bmatrix} = \begin{bmatrix} \lambda_0 & 0 \\ 0 & \lambda_1 \end{bmatrix}
최종적으로 ana_n은 다음과 같다.
[anan−1]=[1210]n−1[10]=[211−1][2n−100(−1)n−1][131313−23][10]=[211−1][2n−100(−1)n−1][1313]=[211−1][2n−13(−1)n−13]=[2n−(−1)n32n−1−(−1)n−13]\begin{aligned} \begin{bmatrix} a_n \\ a_{n-1} \end{bmatrix} & = \begin{bmatrix} 1 & 2 \\ 1 & 0 \end{bmatrix}^{n-1} \begin{bmatrix} 1 \\ 0 \end{bmatrix} \\ & = \begin{bmatrix} 2 & 1 \\ 1 & -1 \end{bmatrix}\begin{bmatrix} 2^{n-1} & 0 \\ 0 & (-1)^{n-1} \end{bmatrix}\begin{bmatrix} \frac{1}{3} & \frac{1}{3} \\ \frac{1}{3} & -\frac{2}{3} \end{bmatrix}\begin{bmatrix} 1 \\ 0 \end{bmatrix} \\ & = \begin{bmatrix} 2 & 1 \\ 1 & -1 \end{bmatrix}\begin{bmatrix} 2^{n-1} & 0 \\ 0 & (-1)^{n-1} \end{bmatrix}\begin{bmatrix} \frac{1}{3} \\ \frac{1}{3} \end{bmatrix} \\ & = \begin{bmatrix} 2 & 1 \\ 1 & -1 \end{bmatrix}\begin{bmatrix} \frac{2^{n-1}}{3} \\ \frac{(-1)^{n-1}}{3} \end{bmatrix} \\ & = \begin{bmatrix} \frac{2^{n} - (-1)^{n}}{3} \\ \frac{2^{n-1} - (-1)^{n-1}}{3} \end{bmatrix} \\ \end{aligned}
an=2n−(−1)n3 a_n = \frac{2^{n} - (-1)^{n}}{3}
끝.
Made with