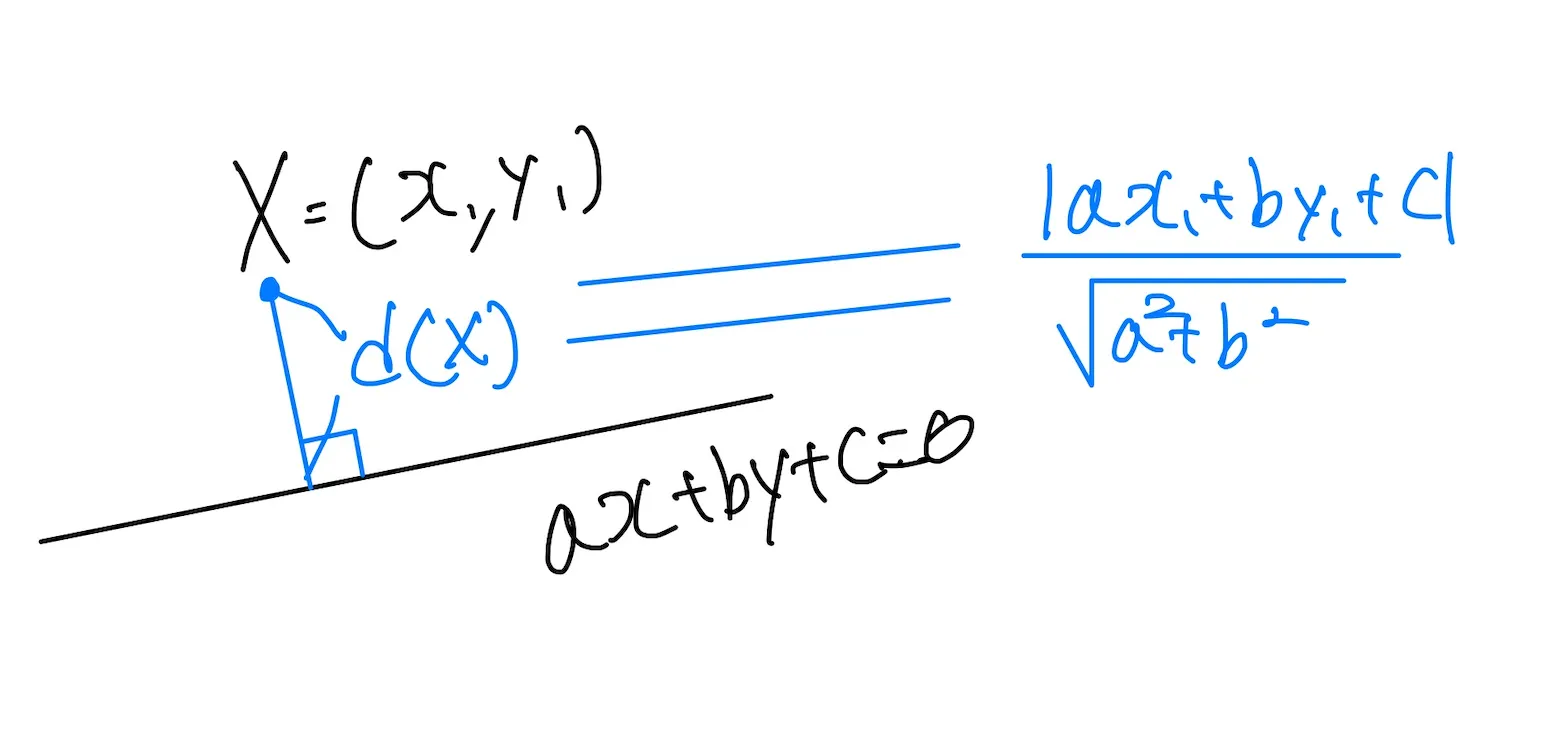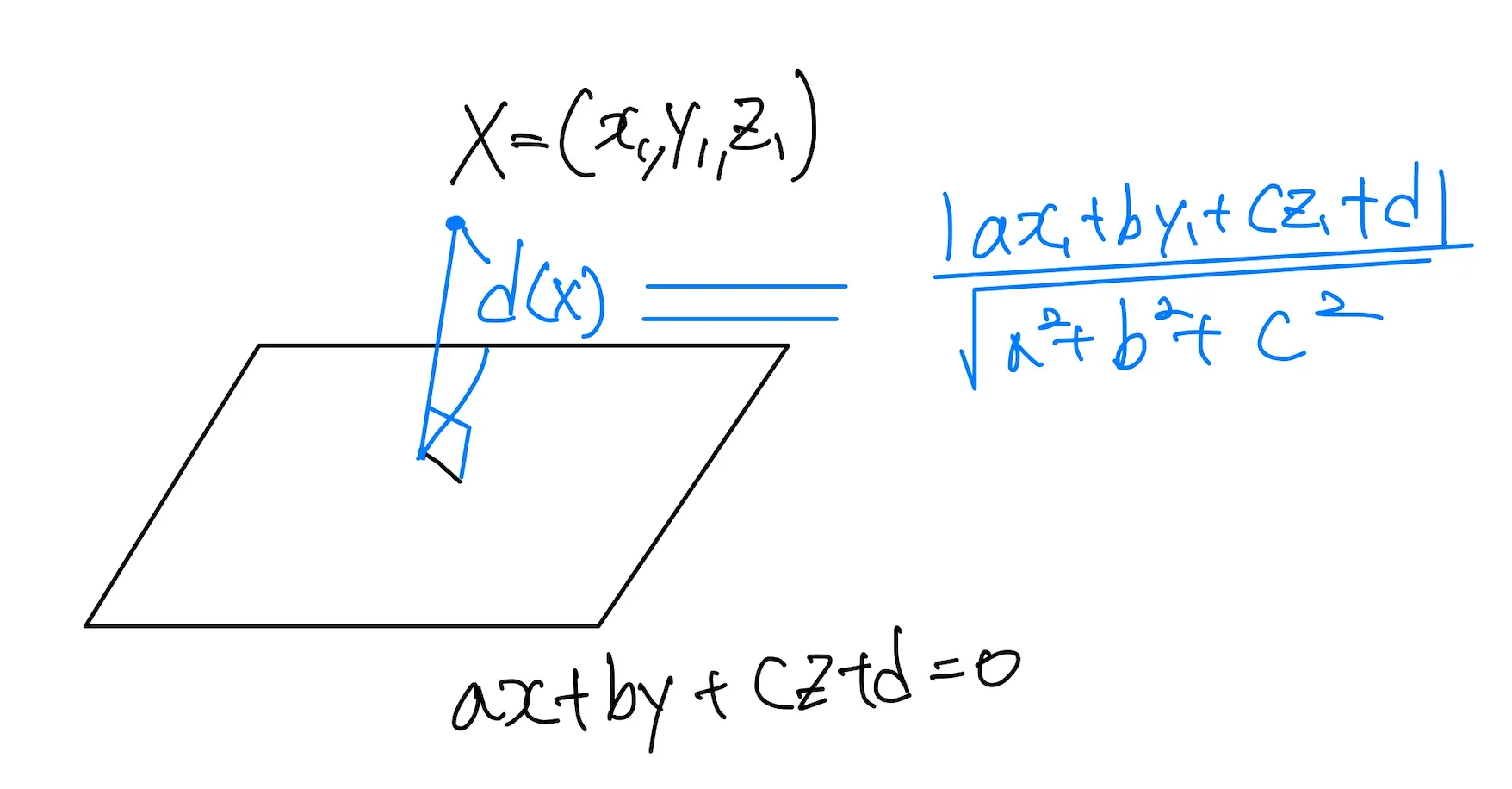Search
Duplicate
☸️

점과 평면 사이의 거리

간단소개
팔만코딩경 컨트리뷰터
ContributorNotionAccount
주제 / 분류
수학
Scrap
태그
수학
9 more properties
학창시절 여러분은 (아마?)
‘점과 직선 사이의 거리’, ‘점과 평면 사이의 거리’ 라는 이름의 공식을 외웠을겁니당
라든가
이런 그림들을 보면서요..!

근데 왜그럴까요?

미리 알고있어야 하는 지식

‘유클리드 공간의 두 벡터를 내적해서 0 나오면 수직이라는 사실’

자 우리는 어른이니까 고작 3차원 말고 임의의 자연수 n차원에서 생각해봅시다.
초평면(3차원 이상의 공간에서는 ax+by+cz+...+C=0ax+by+cz+...+C=0 꼴로 나타나는 부분집합을 차원과 관계없이 초평면이라고 부른대용) ll과 임의의 점 XX를 생각합시다.
X=(x1,x2,...,xn)X=(x_1,x_2,...,x_n) (상수아님) ⇒ Rn\R^n 공간 안의 임의의 점 XX의 위치는 최소 nn개의 실수로 나타낼 수 있습니다. 평면 l:a1x1+a2x2+...+anxn+a0=0l : a_1x_1+a_2x_2+...+a_nx_n+a_0=0 은 이렇게 식으로 써진다고 생각해봅시다. P=(p1,p2,...,pn)P=(p_1,p_2,...,p_n) (상수임) ⇒ PP 는 평면 ll 위의 정점입니다.
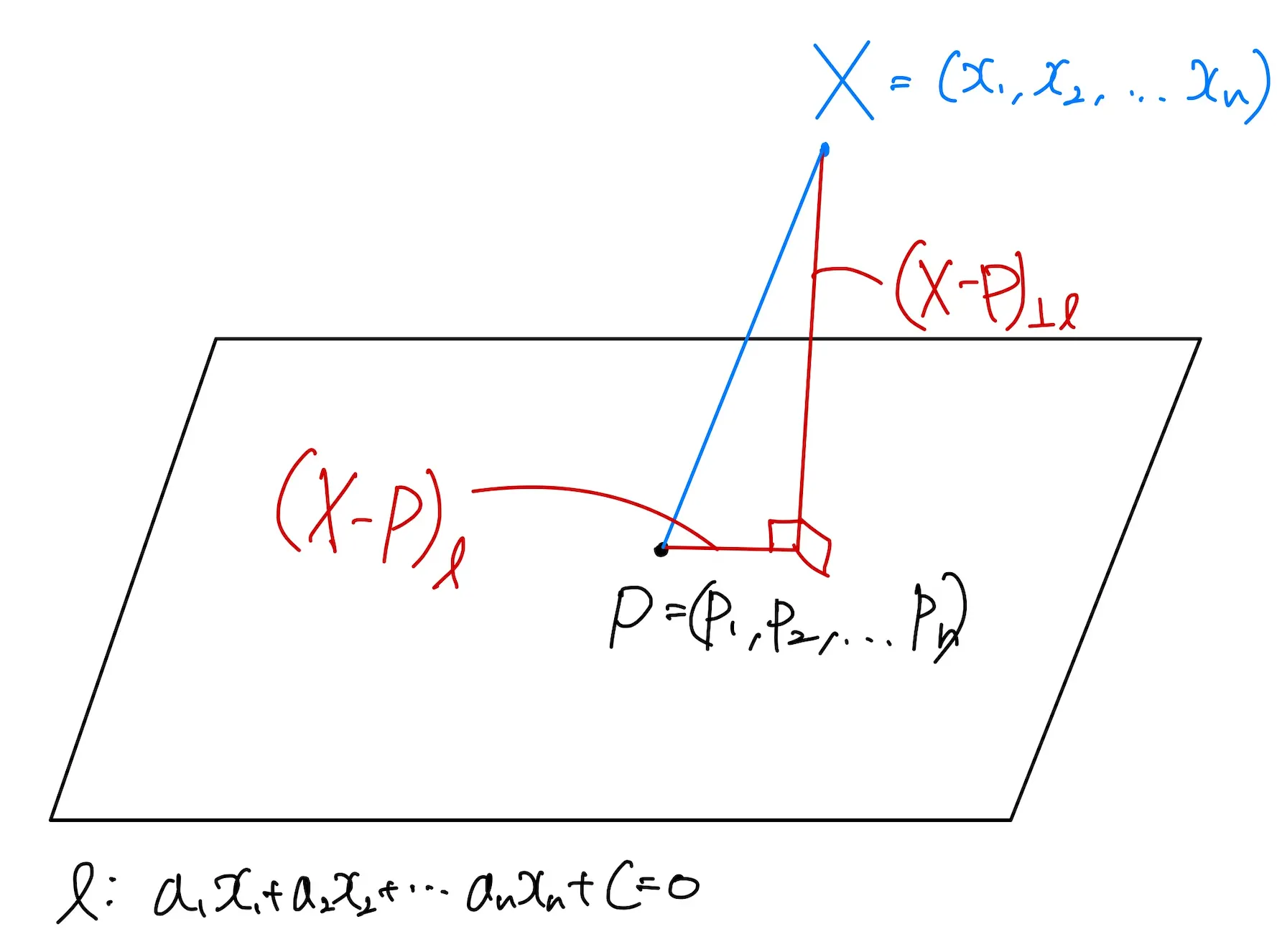
n차원이라서 그림으로 표현할 수는 없지만 대충 이런 느낌 (평면 ll 식 맨 뒤에 CC 는 상수라는 뜻으로 쓴건데 그냥 a0a_0로 쓰겠습니다..! ㅇㅅㅇa 그림 고치기 귀찮네용 ㅎㅎ)
근데 상수 n개짜리 순서쌍 하나만 더 씁시다. 평면 ll의 계수들을 순서쌍으로 만들어서 A=(a1,a2,...,an)A=(a_1,a_2,...,a_n) 라고 할게요 그러면 A⋅X+a0=0A\cdot X + a_0 =0 맞죠?
PP는 평면 ll 위의 점이니까. ll의 식에 P=(p1,p2,...,pn)P=(p_1,p_2,...,p_n)을 대입하면 식이 성립해야겠죠? (즉, a1p1+a2p2+...+anpn+a0=0a_1p_1+a_2p_2+...+a_np_n+a_0=0 입니다용.. 짧게쓰면 A⋅P+a0=0A\cdot P +a_0=0 입니닷)
자, 위의 친절한? 삽화에서 알 수 있듯이 X−P→=(X−P)→l+(X−P)→⊥l\overrightarrow {X-P} = \overrightarrow {(X-P)}_l + \overrightarrow {(X-P)}_{\bot l} 로 나눌 수 있습니다. (대충 평면 ll에 평행한 성분과 수직한 성분이라는 뜻) 자 여기서 A=(a1,a2,...,an)A=(a_1,a_2,...,a_n) 가 평면 ll와 수직이라는 사실을 깨달을 수 있습니다. l:a1x1+a2x2+...anxn+a0=0l:a_1x_1+a_2x_2+...a_nx_n+a_0=0 이고 −A⋅P=a0-A\cdot P = a_0 이죠? 평면 ll을 A,P,XA, P, X의 식으로 나타낼 수 있는데, l:A→⋅(X−P)→=0l : \overrightarrow A\cdot\overrightarrow{(X-P)}=0 입니다. 만약 XX가 평면 ll위의 점이라면 X−P→=(X−P)l→+(X−P)⊥l→\overrightarrow {X-P} = \overrightarrow {(X-P)_l} + \overrightarrow {(X-P)_{\bot l}} 에서 (X−P)⊥l→=0⃗\overrightarrow {(X-P)_{\bot l}}=\vec 0 이거든요 그러면! A→⋅(X−P)→=A→⋅(X−P)l→=0\overrightarrow A\cdot \overrightarrow{(X-P)}= \overrightarrow A\cdot \overrightarrow{(X-P)_{l}}=0 이 되고, 모든 평면 위의 벡터에 대해 AA가 수직임을 알 수 있습니다.
Example
알기 쉽게 예를 들자면 x+2y+3z=Cx+2y+3z= C 평면은, (1,2,3)→\overrightarrow{(1,2,3)}와 수직인 것이죠 (x0,y0,z0)(x_0,y_0,z_0) 는 x0+2y0+3z0=Cx_0+2y_0+3z_0=C를 만족한다. ⇔(x0,y0,z0)\Leftrightarrow (x_0,y_0,z_0)가 평면 위에 있습니다. 일 때 (1,2,3)→⋅(x,y,z)−(x0,y0,z0)→=0\overrightarrow{(1,2,3)}\cdot\overrightarrow{(x,y,z)-(x_0,y_0,z_0)}=0 인 것입니다.

아니 그래서 거리는 어떻게 구하는건가용?

위에서 언급한 ∣(X−P)⊥l→∣=d(X)|\overrightarrow{(X-P)_{\bot l}}|=d(X) 이 곧 점 XX와 평면 ll 사이의 거리가 되는데요 우리는 위에서 A→⋅(X−P)→=A→⋅(X−P)l→+A⋅(X−P)⊥l→\overrightarrow A\cdot \overrightarrow{(X-P)}= \overrightarrow A\cdot { \overrightarrow{(X-P)_l} + A\cdot \overrightarrow{(X-P)_{\bot l}}} 이고 A⋅(X−P)l→=0A\cdot \overrightarrow {(X-P)_l}=0 임을 알았습니다. 그러면 A→⋅(X−P)→=A⋅(X−P)⊥l→\overrightarrow A\cdot \overrightarrow{(X-P)}= A\cdot \overrightarrow{(X-P)_{\bot l}} 이고 d(X)=∣(X−P)⊥l→∣=∣A→⋅(X−P)→∣∣A→∣=∣a1x1+a2x2+...+anxn+a0∣a12+a22+...+an2d(X) = |\overrightarrow{(X-P)_{\bot l}}| = \frac{|\overrightarrow A\cdot \overrightarrow{(X-P)}|}{|\overrightarrow A|} = \frac {|a_1x_1+a_2x_2+...+a_nx_n+a_0|}{\sqrt{a_1^2+a_2^2+...+a_n^2}} 가 됩니다. 우리가 아는 거리공식 ∣ax1+by1+cz1+d∣a2+b2+c2 \frac {|ax_1+by_1+cz_1+d|}{\sqrt{a^2+b^2+c^2}}를 일반적으로 나타낸 것이지요..!
어렵진 않았죠?
Made with