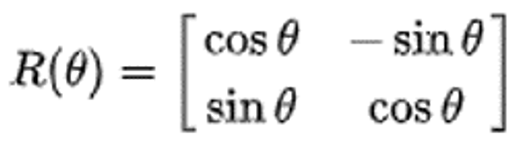저번 글에 이어서 정리하도록 할게요!
FDF
FDF를 하면서 배운 것들
2. 선형 보간법
fdf파일에는 좌표 뿐만이 아니라 색깔에 대한 정보도 가지고 있다. 서로 다른 색깔의 두 점을 이어줄 때 색깔을 자연스럽게 바꿔주어야 하는데 어떻게 바꿔야 할까??
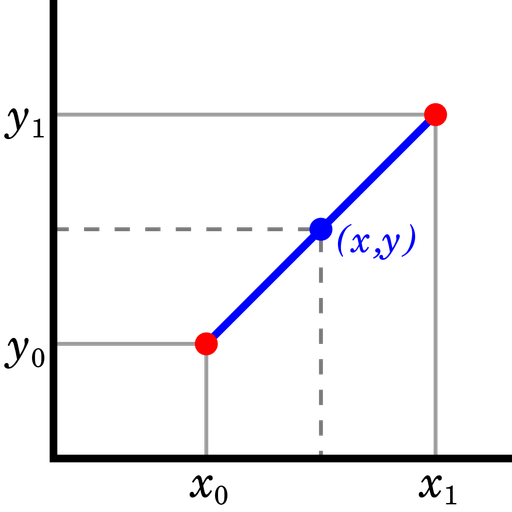
선형 보간법 : 끝점의 값이 주어졌을 때 그 사이에 위치한 값을 추정하기 위하여 직선 거리에 따라 선형적으로 계산하는 방법
.jpg&blockId=558072a9-2e2b-4fa4-a683-a7e73c7ad8bc)
선형 보간법
사실 선형 보간법 개념 자체는 많이 익숙한 개념이기 때문에 크게 어렵지는 않을 것이다. 해당 점이 현재 어느 정도에 위치해 있는지 비율을 구하고 해당 비율만큼 값을 변경해주면 된다. 단, 조심해야 할 점이 몇 가지 있다.
1.
그라데이션이 자연스럽게 나오도록 하기 위해 x값과 y값 중 변화가 큰 값을 기준으로 비율을 구하기
•
필기에 case1을 보면 x값을 통해 값을 나누면 색깔이 3가지로 나뉘지만 y값을 기준으로 나누면 8가지로 나뉠 것이다.
2.
우리는 색깔을 TRGB방식을 통해 나타낸다.
•
TRGB방식은 색깔에 대한 값을 int형으로 받는다. int형의 4바이트에서 각각 1바이트씩 transparency, red, green, blue를 나타낸다.
•
단순히 색깔 값을 선형보간법으로 구하면 예상치 못한 색깔이 나올 수 있다.
◦
0x000000 와 0xFF0000사이의 색깔을 나타낼 때 단순히 red값만 바뀌어야 하는데 green, blue 값의 색깔도 들어가게 된다.
◦
그렇기 때문에 각 바이트 별로 색깔을 나눠서 값을 구해야 한다.
get_color
3. 회전 변환
2차원 회전 변환
sin, cos 덧셈 공식?
sin(x + y) = sin(x)cos(y) + cos(x)sin(y)
cos(x + y) = cos(x)cos(y) - sin(x)sin(y)
.jpg&blockId=6b3ec786-59dd-4d08-a5cf-f4d58294d5fc)
2차원에서 좌표(x, y)를 a만큼 회전시키면 (x’, y’) = (x*cos(a) - y*sin(a), x*sin(a) + y*cos(a))
만약 원점이 아닌 점을 기준으로 회전할 때
회전하는 기준을 원점으로 평행이동 → 회전 → 다시 원위치
3차원 회전 변환
.jpg&blockId=f28ba7be-2428-47f5-b681-ab525bb0a7a2)
2차원 회전 변환에서 했던 대로 각 축 별로 똑같이 계산하면 된다.
•
인터넷에서 공식이 나와있긴 한데 실제로 그렇게 계산했을 때 회전 방향이 반대로 돌아가는 문제가 있었다.
((+)방향으로 돌렸는데 (-)방향으로 돌아감)
•
서로 그림의 좌표축이 달라서 생긴 문제.
•
내 좌표축대로 다시 계산해서 적용하니 내가 의도한 대로 회전이 되었다.
rotate_axis
4. 등각 투영
.jpg&blockId=06aaad80-0ce2-41fc-adb8-25dc7f3814b5)
•
isometric같은 등각 투영 시 3차원 좌표를 모니터 상에 2차원 좌표로 표현을 해야한다.
•
그 때 각 x, y, z좌표가 2차원 평면에서 어디에 위치해있는지를 구하고 각각을 더해주면 끝.
•
fdf 맵에서 y값은 아래로 내려갈수록 증가하고 3D상에서 z축은 위로 갈수록 증가하므로 서로 부호가 반대인 것 조심!
.jpg&blockId=9ab20966-5272-4324-aa95-596ddc6e8d75)
P(x, y, z) → P((x - y)*cos(a), (x + y)*sin(a) - z)
마지막으로 제 프로그램의 구성은 이렇습니다.
.jpg&blockId=7b38a3fa-e637-4448-b496-532c740569f9)
5. 기타
점을 모니터에 나타내기
•
점을 모니터에 나타내기 위해 가공할 때 순서
1.
원점으로 이동(가로 길이의 절반만큼 x축 이동, 세로 길이의 절반만큼 y축 이동)
2.
윈도우 크기에 비례하여 점을 확대(화면 픽셀수는 1000인데 가로 길이가 10이면 안되겠죠?? 일정 비율로 좌표들을 확대시켜주세요)
3.
회전(3차원 회전변환)
4.
투영법(직각투영, 등축투영…)에 맞춰서 점 바꿔주기
5.
화면의 가운데로 위치시키기
•
◦
hook을 이용하면 다양한 재밌는 것들을 시도할 수 있으니 꼭 해보시는 걸 추천드려요.
•
color값을 가져올 때 비트연산을 사용하기 때문에 낯설다면 간단히 공부하고 시작하는 것을 추천해요.
color_utils
마치며
이미 팔만코딩경에 mlx나 fdf에 관한 글들이 있기 때문에 그 곳에서 코드를 어떻게 짜야할 지 대략적으로 감을 잡았을 거라 생각해요. 저는 그것보다는 fdf가 어떤 과제인지 알았으면 했고, 어떠한 지식들이 필요한지 알고나서 과제에 들어가면 좋을 것 같다는 생각에 이렇게 글을 썼어요. 제 설명이 부족해서 읽고나서 오히려 더 헷갈릴 수도 있지만 그래도 한 번 흥미를 갖고 해당 과제를 해보는 것도 좋을 것 같아요!!
