Push Swap using Merge Sort
이 글에선 5기 seseo 님이 고안하신 Merge Sort 접근법과, 이를 통해 제 과제에 병합정렬을 적용한 과정을 소개합니다.
100개 정렬
500개 정렬
같은 성능의 병합정렬이여도, 구현 로직이 다르면 위 영상과 정렬 과정이 달라집니다.
“아 삼각형을 계속 합치는 구나~” 정도 감을 잡으시면 좋을 것 같습니다. 병합 정렬 평균 성능
100개 정렬
: ra rb = rr와 같은 명령어 최적화 후 → 평균 620개 500개 정렬
: ra rb = rr와 같은 명령어 최적화 후 → 평균 4480개 1000개 정렬
: ra rb = rr와 같은 명령어 최적화 후 → 평균 9510개 입력값의 분포에 영향받지 않아 명령어 개수가 일정하게 나오는게 장점입니다. 접근 아이디어
: 삼각형들이 어떤 모양으로 있어야 병합하기 좋은가?
분할 : 삼각형 합치기 전 모양을 거꾸로 유추하기 (가정법)
1개의 정렬될 집합을 정렬된 3개의 부분집합으로 분할(예측) 할 수 있습니다.
그리고 이렇게 정렬된 부분 집합은 삼각형의 모양입니다.
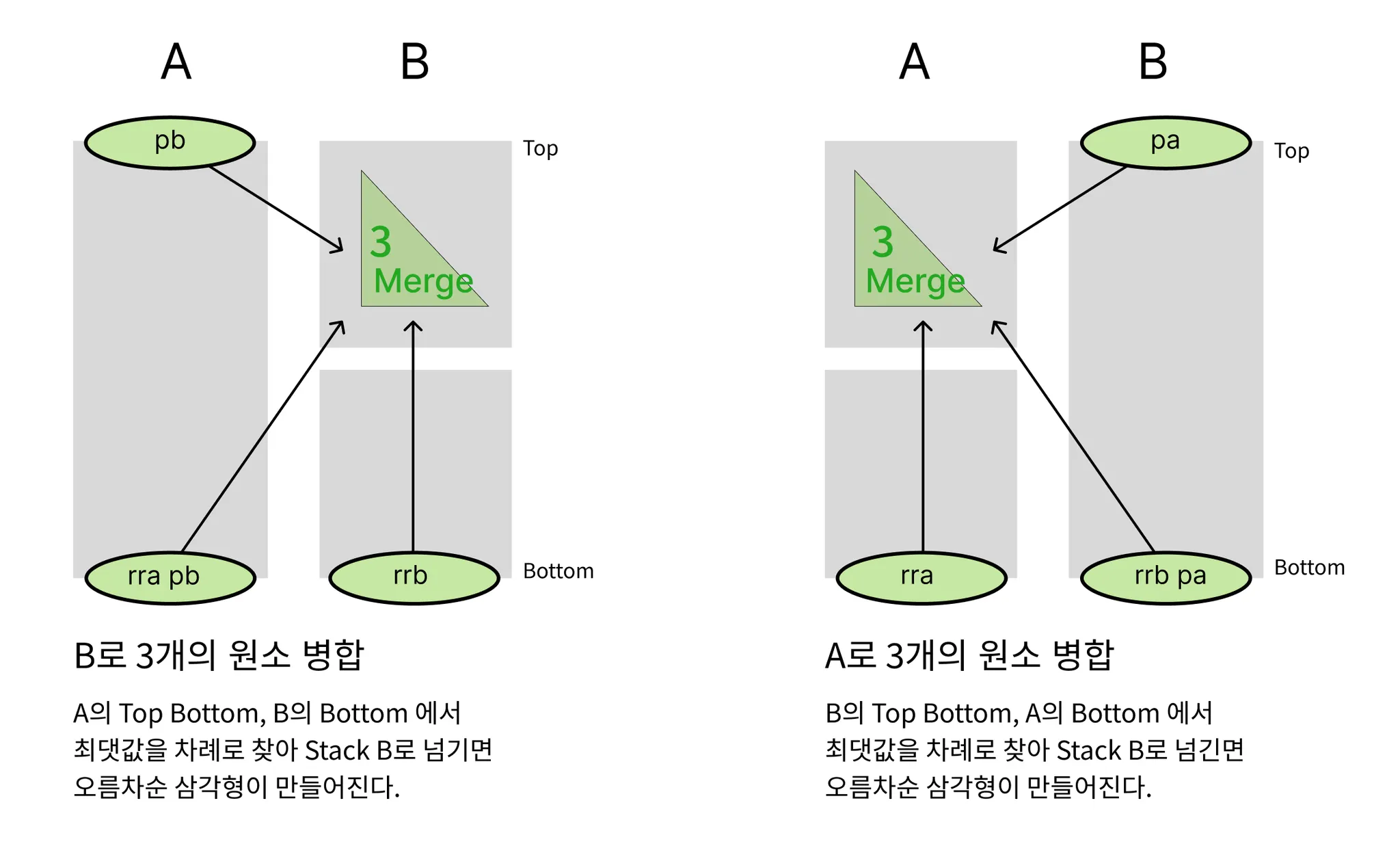
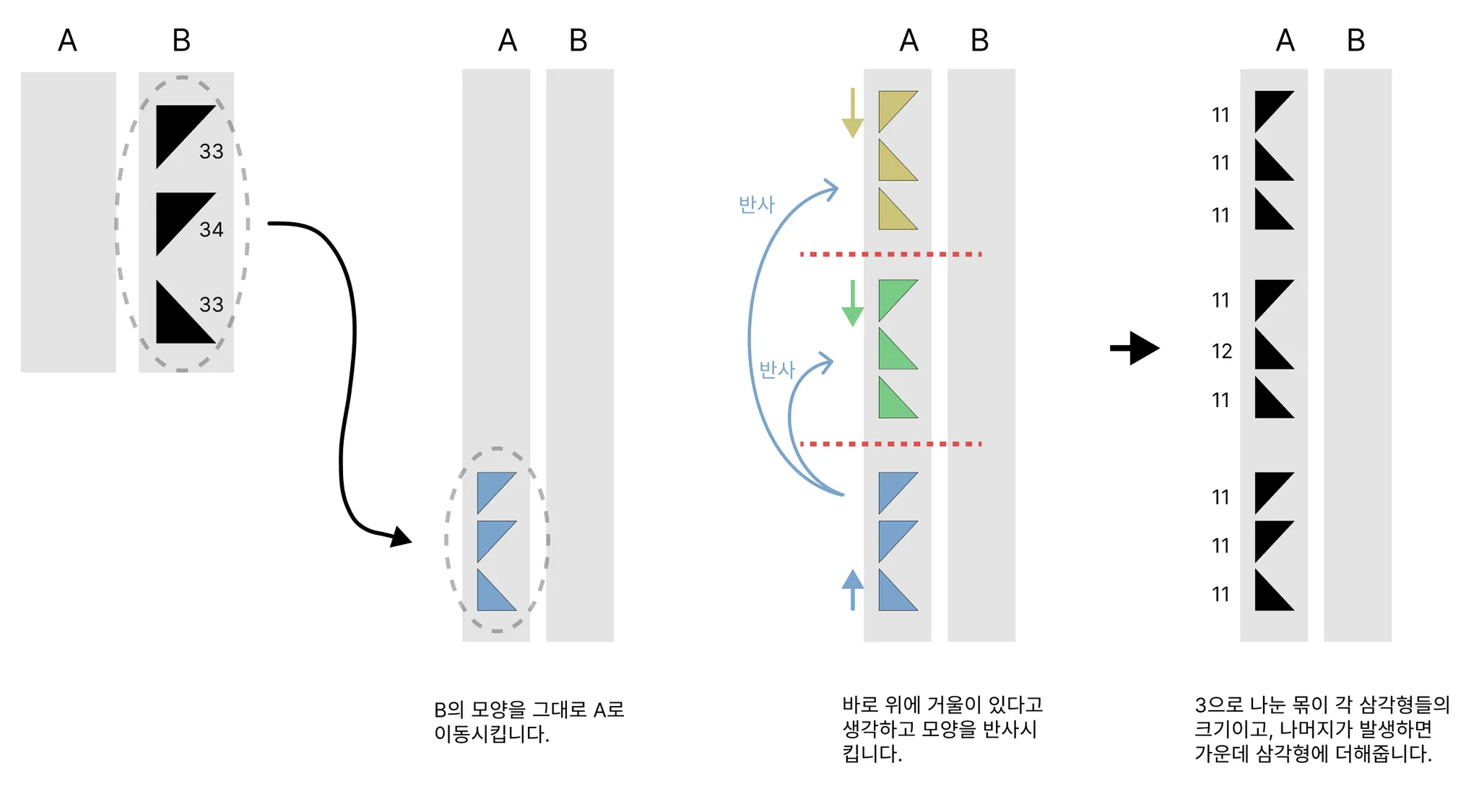
스택의 가장자리 원소들만 비교해서 삼각형(크기=3) 만들기
각 Stack의 Top과 Bottom에 있는 원소중 3개를 선택하여 비교합니다.
이를 빈 공간에 정렬하면 가장 적은 명령어 횟수로 빈 공간에 크기3의 삼각형을 만들 수 있습니다.
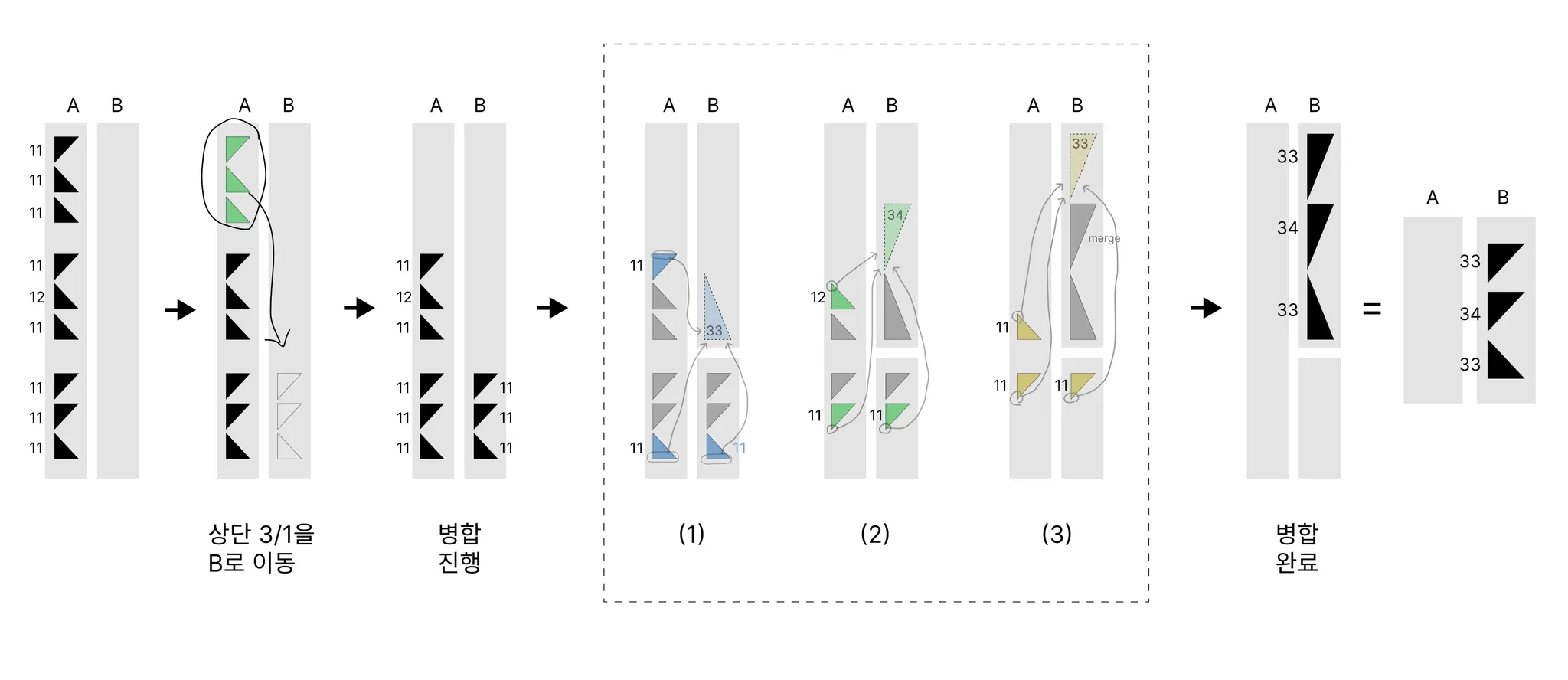
삼각형 3개를 병합하기
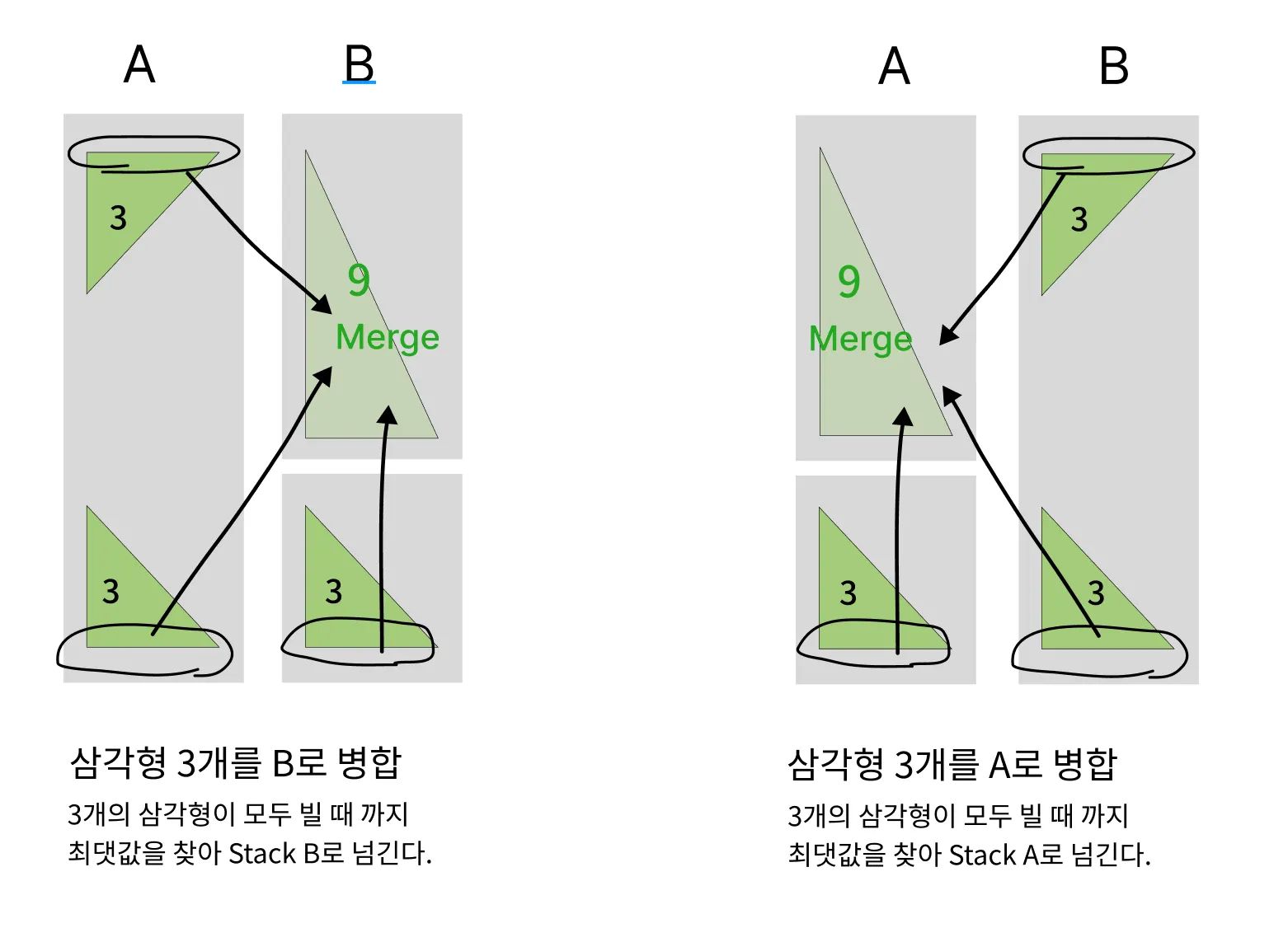
위 과정을 삼각형을 병합할 때 이용하겠습니다.
이번에는 삼각형 3개가 아래 그림처럼 있다고 볼께요.
스택의 가장자리에 있는 원소들 중에서 최댓값 or 최솟값을 찾아 병합하는 과정을
삼각형이 모두 없어질 때 까지 반복하면 삼각형 1개로 병합할 수 있습니다.
오름차순 = 삼각형 3개중 최댓값을 찾아 push
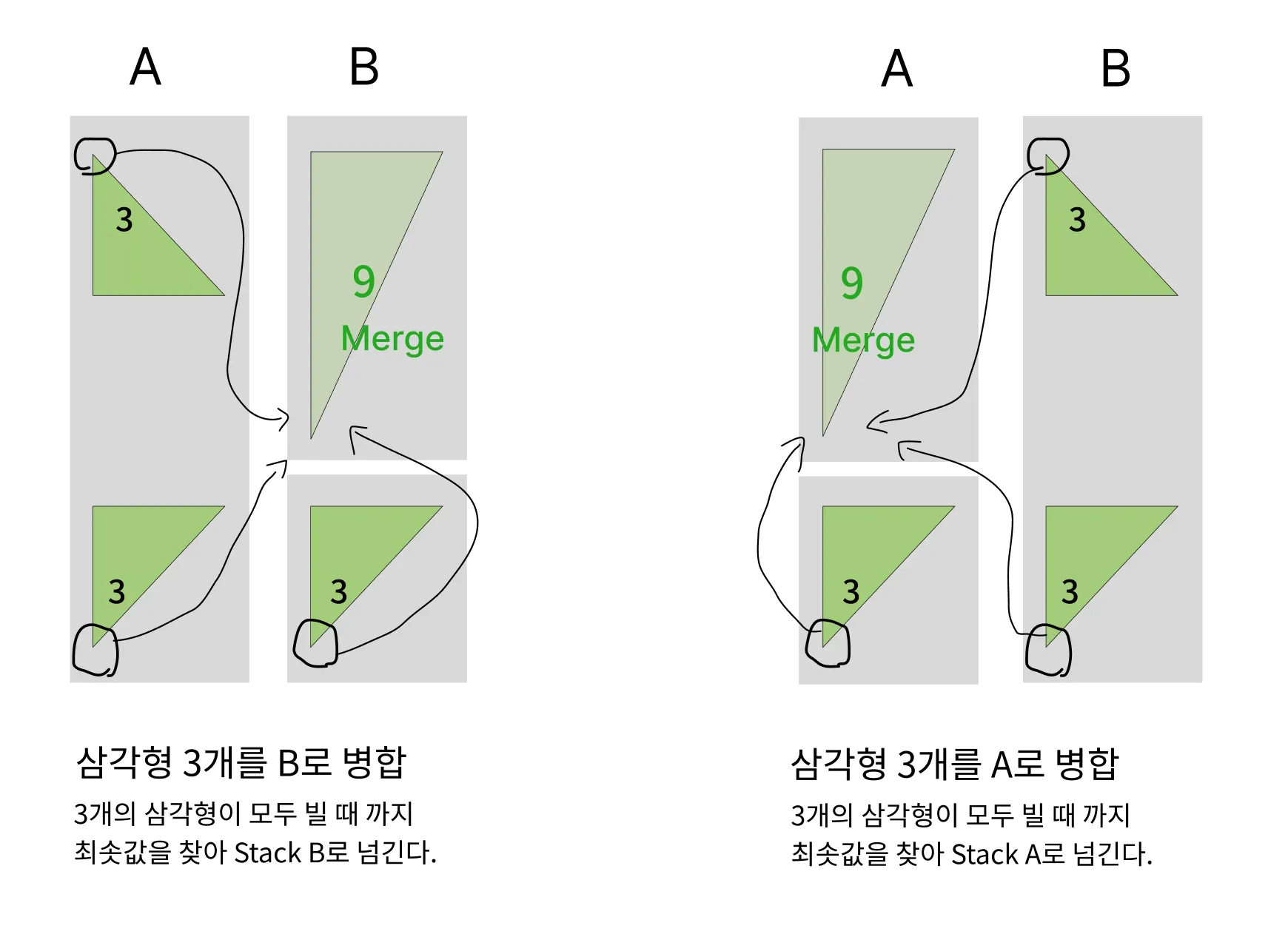
내림차순 = 삼각형 3개중 최솟값을 찾아 push
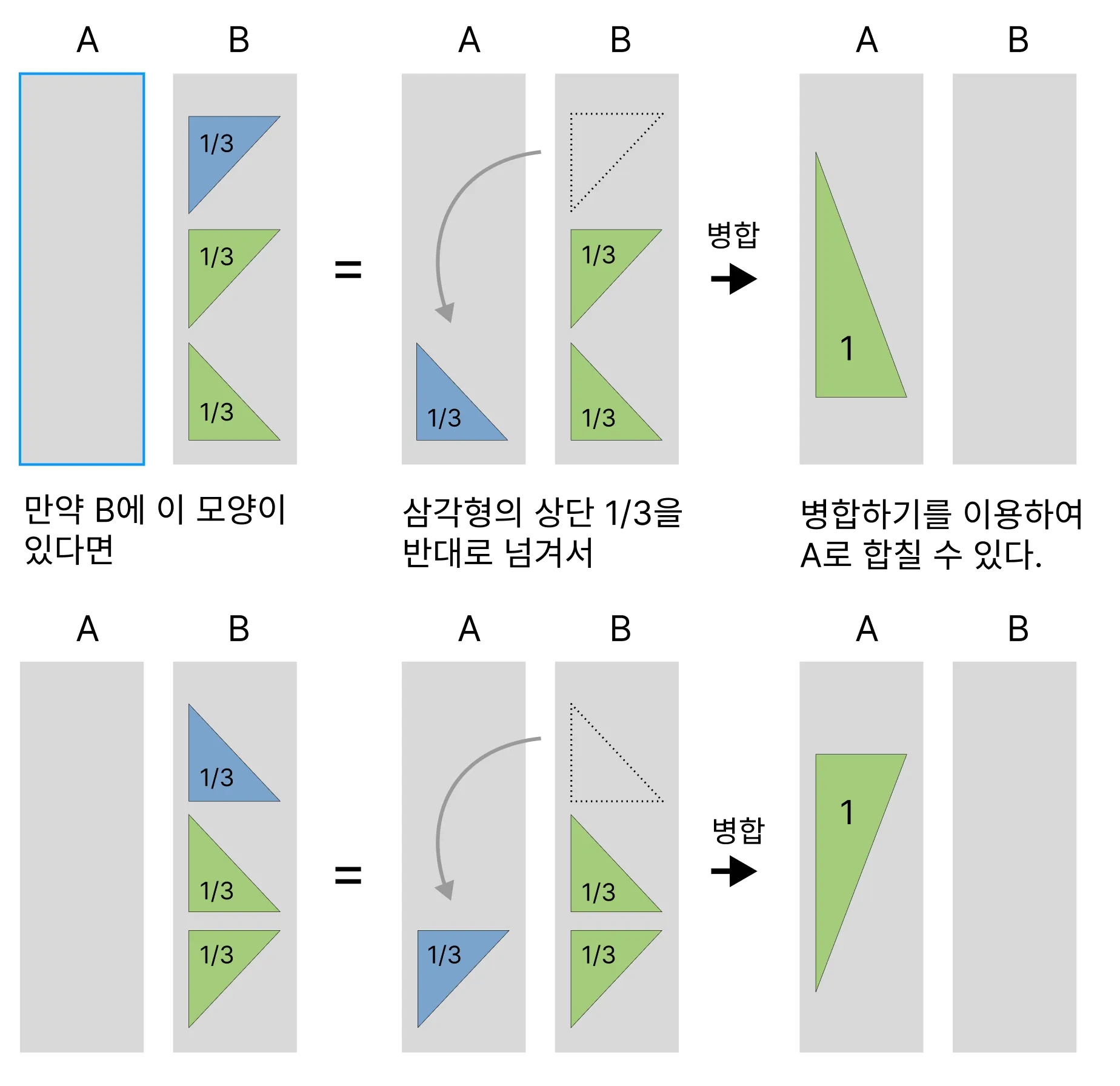
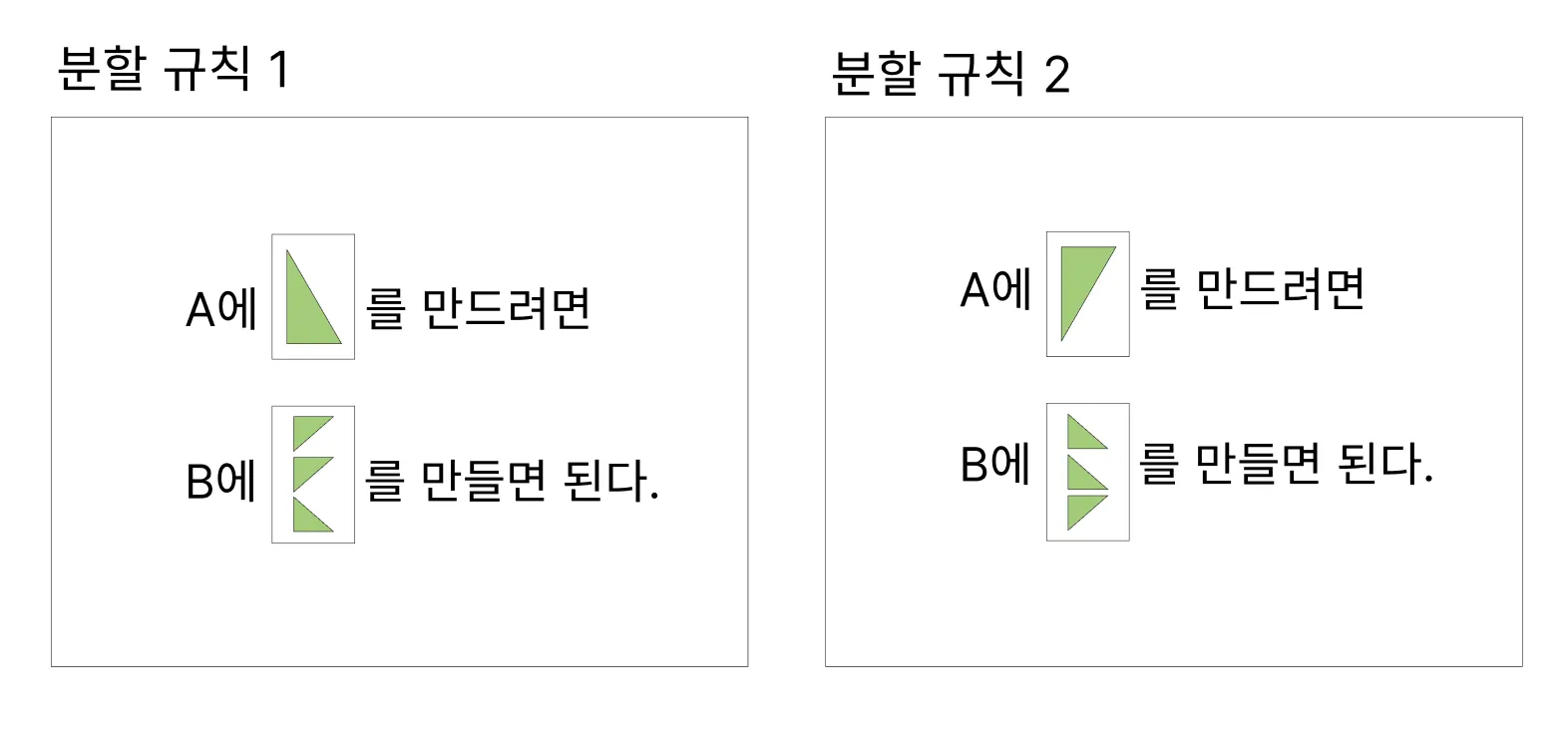
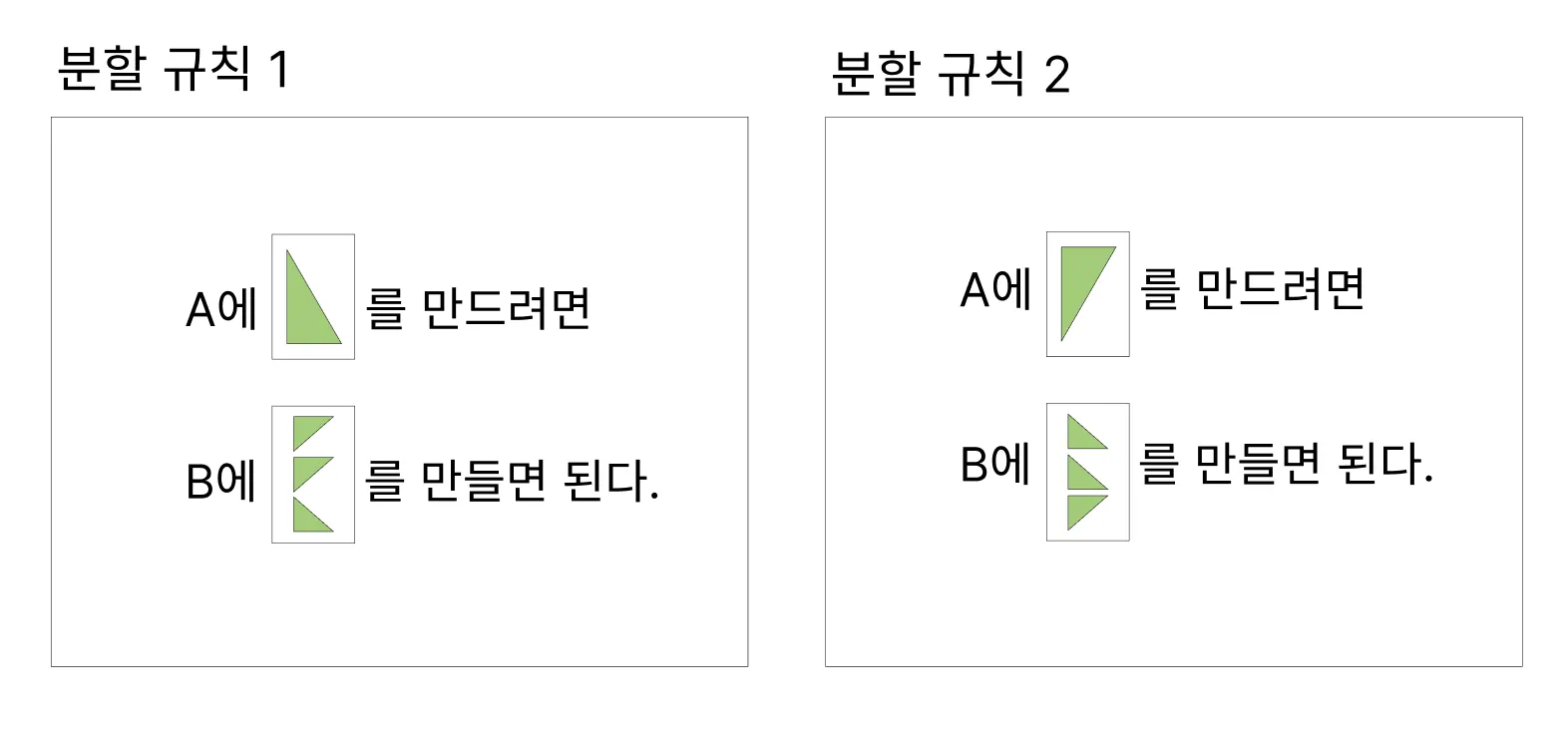
삼각형 분할 규칙
1개의 삼각형이 3개의 삼각형으로 분할되는 과정은 아래처럼 정리할 수 있습니다.
이 규칙을 가지고 1개의 삼각형을 3개의 작은 삼각형으로 분할할 수 있습니다.
입력값이 N일때, 분할한 삼각형들을 3개씩 합쳐 크기 N의 삼각형을 만드는 것이 병합정렬의 key 아이디어입니다.
위 분할 규칙이 아래 그림에서 사용됩니다.
여기까지 보셨다면 필요한 병합정렬 아이디어는 끝입니다.
다만 배열이 아닌 스택을 이용해야 하기 때문에, 구현자가 선택한 자료구조(데크, 동적 배열, etc…) 및 분할&병합 순서에 따라 정렬 과정이 달라질 수 있습니다.
위 아이디어를 활용해서 병합 정렬 과정을 구현하시면 됩니다. 종이에 삼각형들을 그려가면서 구현해보세요.
•
구현시 고민해볼 거리들
◦
크기 27의 삼각형을 어떻게 분할하고 병합할 것인가?◦
크기 81의 삼각형을 어떻게 분할하고 병합할 것인가?◦
크기 100의 삼각형은?◦
3개의 삼각형로 계속 나눌경우 발생한 나머지는 어떻게 처리할 것인가?
(ex. 100 = 33 + 33 + 33 + 1) 적용 : 병합하기 좋은 모양 만들기
이제 위 아이디어를 바탕으로 제가 적용한 풀이 과정을 설명드리겠습니다.
9개의 삼각형이 어떤 모양으로 있어야, 병합했을 때 원하는 모양의 3개의 삼각형이 될까?
과제를 진행하며 주로 했던 고민은
“1개를 3개로 분할하는건 알겠는데, 3개의 삼각형을 어떤 모양의 9개로 분할하는가?” 였습니다.
다행히도 병합에 최적인 최소 삼각형들의 모양에는 일정한 규칙(패턴) 있습니다. 이 패턴을 이용하면 3개의 삼각형을 9개의 삼각형으로, 다시 27개의 삼각형으로, 다시 81개의 삼각형으로 쉽게 연속 분할할 수 있습니다.
삼각형 분할 패턴 (거울, Mirroring)
예제 : 크기 100의 삼각형을 연속해서 분할하기
분할 규칙1과 2를 잘 보시면, 맨 밑 삼각형을 기준으로 위 2개가 대칭을 이룹니다.
이 규칙을 이용해서 한번 계속 분할해보겠습니다.
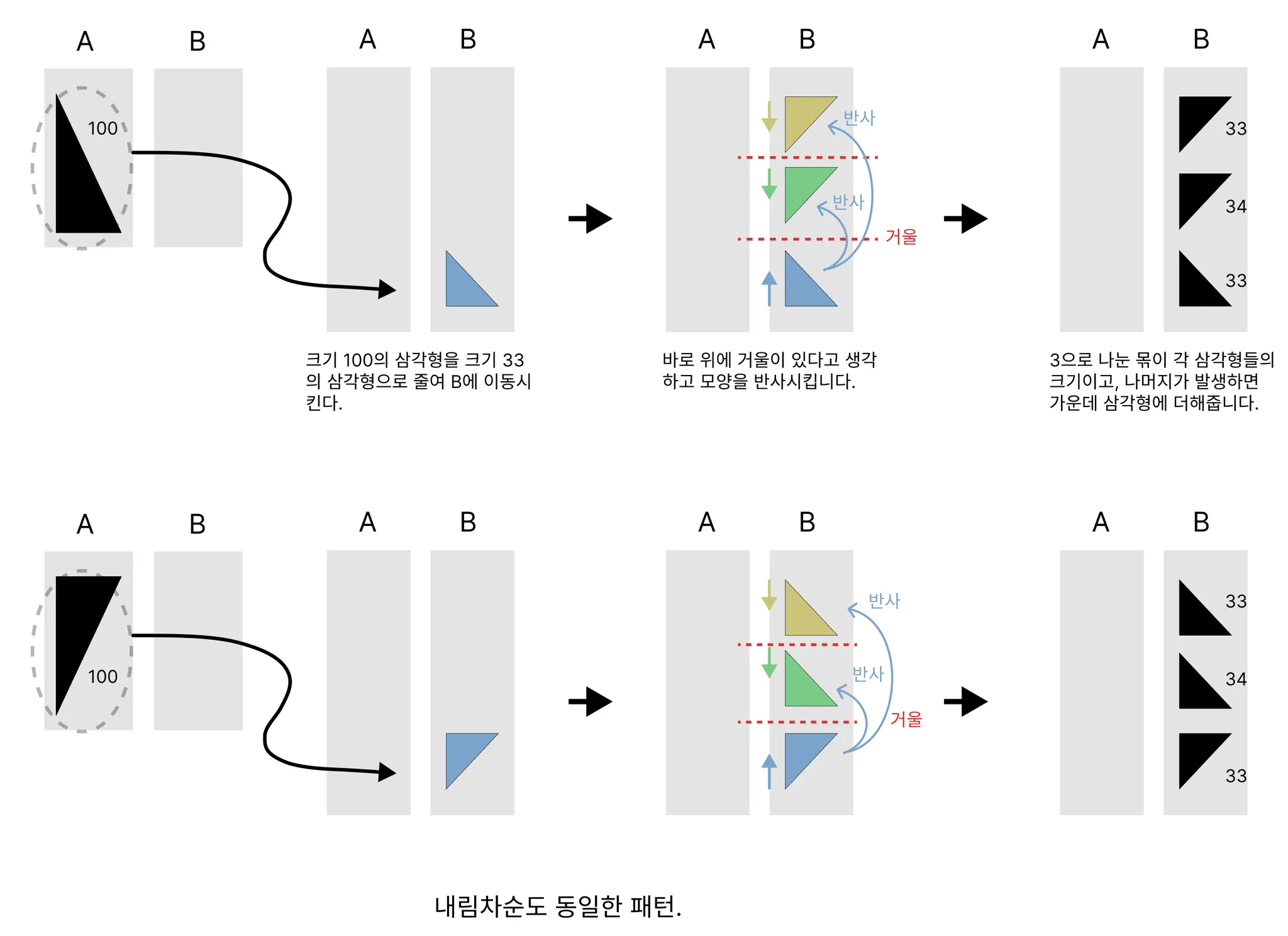
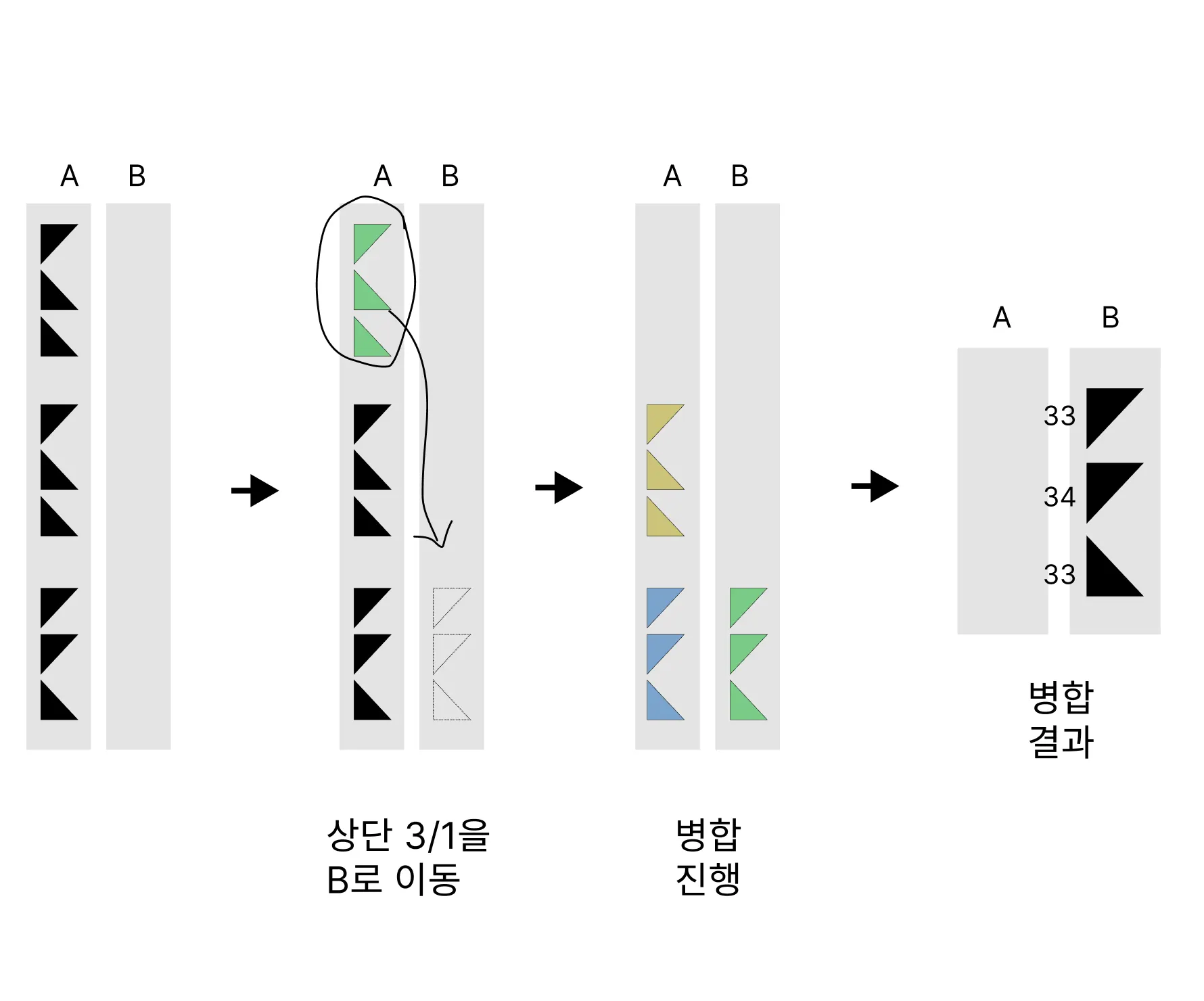
100개의 첫번째 분할
100 = (33 + 34 + 33)
•
분할
•
병합하면 원래대로(분할 전 모양) 돌아옴을 확인
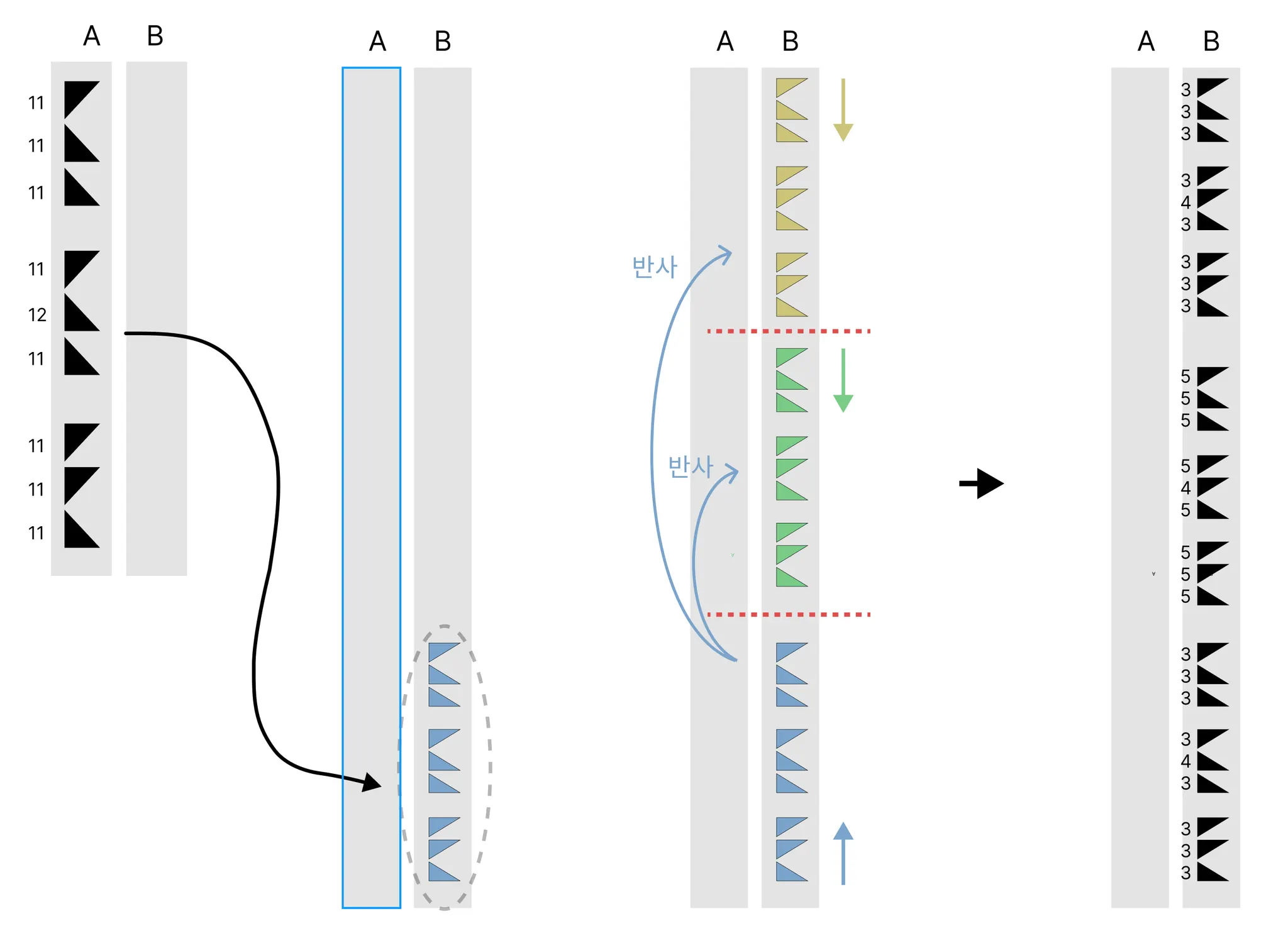
똑같은 규칙으로 2번째 분할하기.
(33 + 34 + 33) = (11+11+11)+(11+12+11)+(11+11+11)
•
분할
삼각형 3개를 거울 반사(대칭) 규칙을 이용하여 다시 9개의 삼각형들로 재분할합니다.
•
병합해보면 원래대로(분할 전 모양) 돌아옴을 확인.
분할한 9개의 삼각형을 동일한 로직으로 병합하면 처음 3개 모양으로 합쳐지는 걸 확인할 수 있습니다.
세번째 분할하기
(11+11+11) = (3+5+3) + (3+5+3) + (3+5+3)
(11+12+11) = (3+5+3) + (4+4+4) + (3+5+3)
이제 같은 방법으로 9개를 27개로 재분할해보겠습니다.
이걸 거꾸로 병합하면 원상복구 되겠죠.
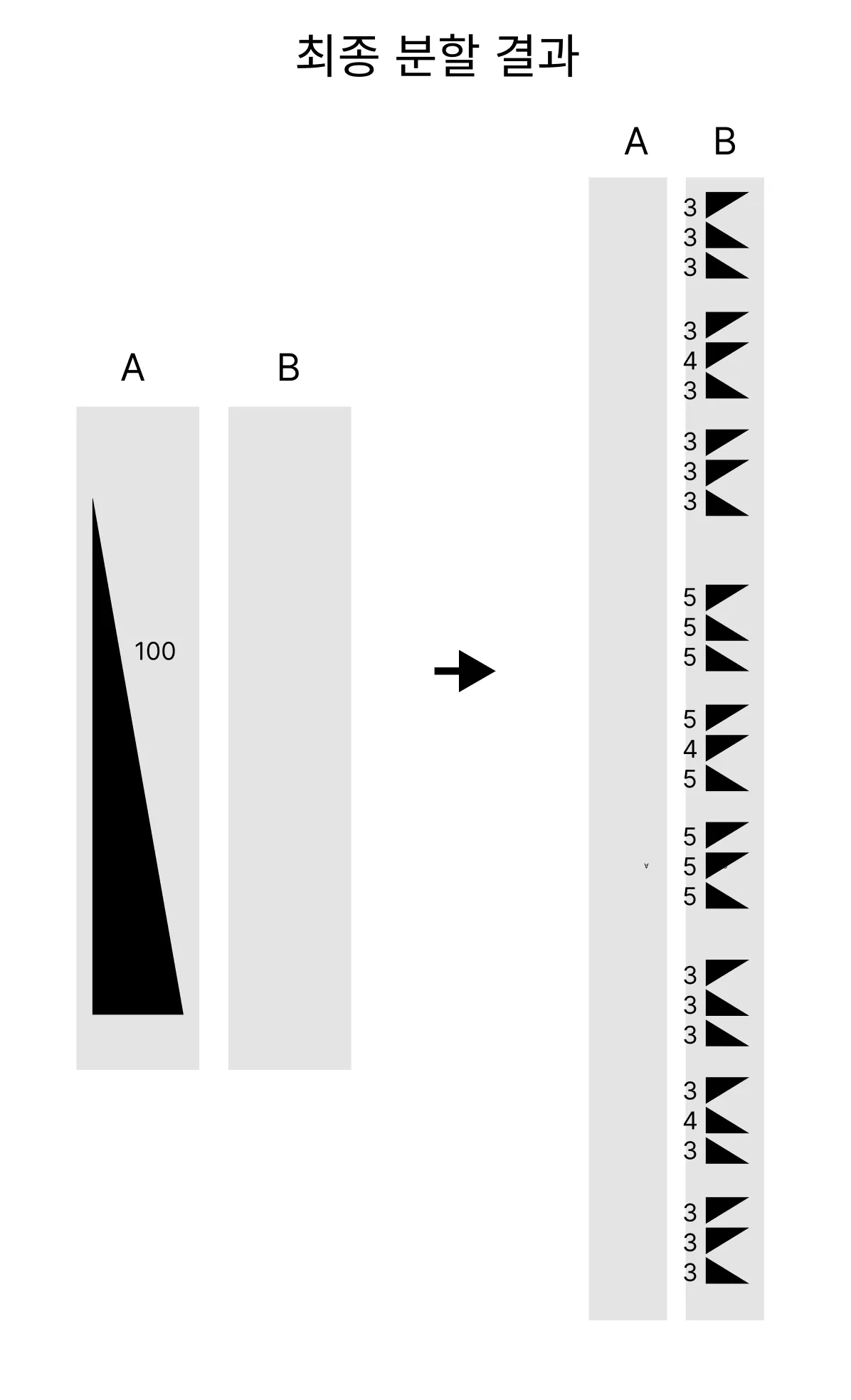
최종 분할 결과
여기서 더 분할할 수 있지만, 저는 명령어 횟수를 맞추기 위해 삼각형의 크기가 6 미만일때까지 분할했습니다.
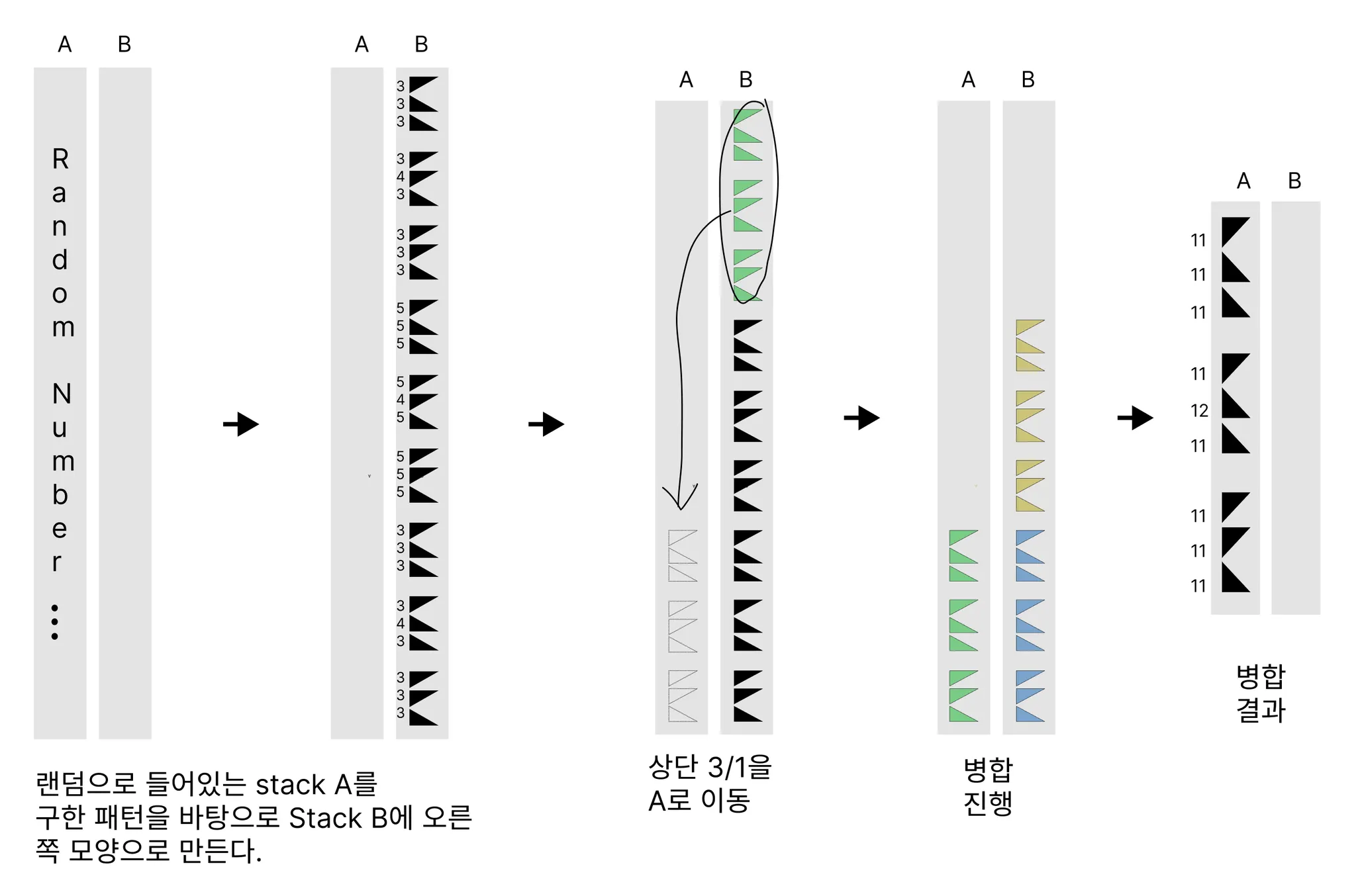
병합하기 좋은 모양을 미리 알아낸 뒤 (삼각형 역추적)
그 설계도를 바탕으로 초기 삼각형 패턴을 Stack B에 똑같이 만듭니다.
이후 병합 → 병합 → 병합 을 진행하면 삼각형들이 Merge되면서 정렬됩니다.
1.
[예측]
정렬될 결과를 역으로 분할해서 병합에 용이한 최소 삼각형들의 모양(패턴)을 미리 알아낼 수 있습니다.
2.
[분할]
정렬이 처음에 시작되면, 최초 Stack A에 쌓인 랜덤한 값들을 Top에서부터 3/4/5개씩 Stack B로 쌓아나가면서 미리 계산한 최대 분할 모양으로 만듭니다.
3.
[병합]
이후 모두 병합될 때 까지 동일한 규칙으로 병합을 반복 합니다.
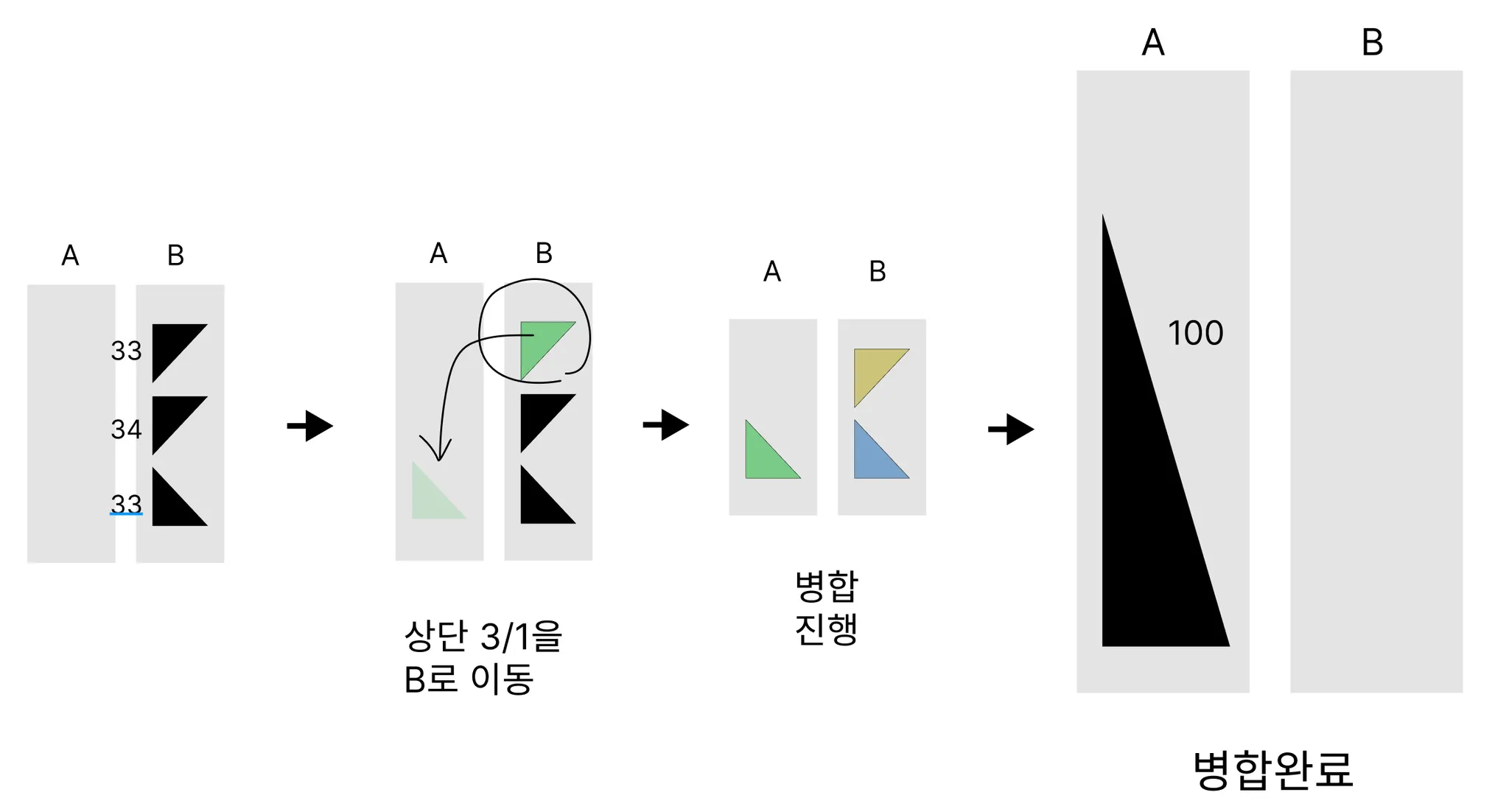
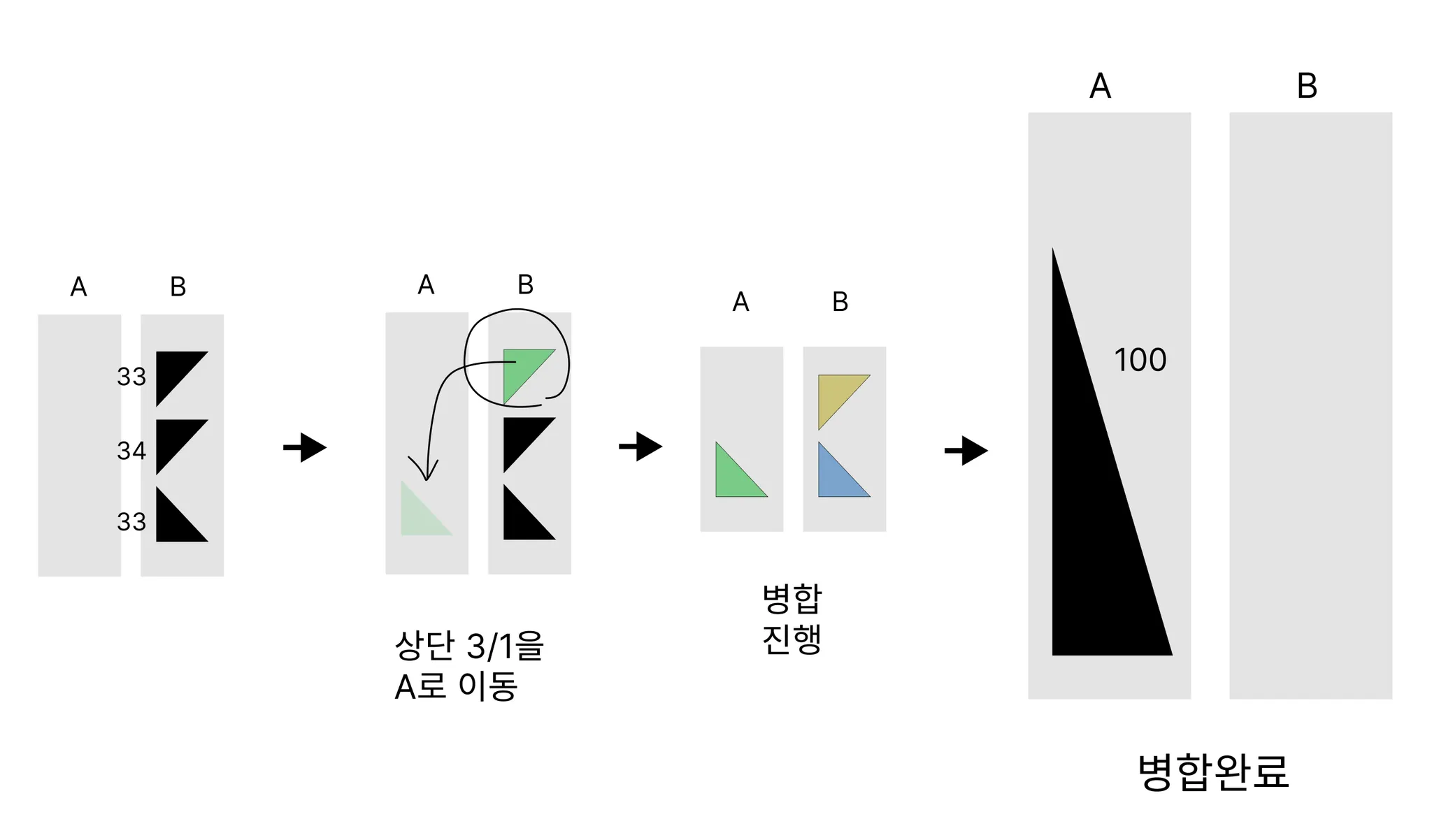
합친 삼각형의 크기가 100이 될 때까지, 삼각형들을 계속해서 병합하면 된다.
이제 병합된 삼각형이 100개가 되었기 때문에 병합을 멈춥니다.
총 3번의 Merge를 거쳐 Stack A에 100개의 데이터가 정렬되었습니다.
위 100개 원소 병합정렬 과정의 비주얼라이저 버전입니다.
삼각형들이 Stack A와 B를 왔다 갔다 하면서 합쳐지는 것이 보이실겁니다.
100개 정렬
위 로직은 정답이 아니라 구현 예시 중 한가지입니다. 구현자님께서 사용하신 자료구조와 분할&병합 로직에 따라 정렬 과정이 달라질 수 있습니다.
이 가이드를 바탕으로 더 빠르고, 효율적인 Merge Sort 로직을 구현해보시길 기대합니다.
개선할 만한 점 (1104 추가 내용)
슬랙으로 많이 질문 주시는 부분, 비효율 적인 부분 정리하였습니다.
구현하실 때 이 부분도 함께 고민해보시면 좋을 것 같아요.
•
sangmiha 님께서 알려주신 분할 과정 비효율성 문제. (알려주셔서 감사합니다!)
1.
17개의 인자가 주어진 경우.
이를 3으로 나눌 경우 5, 7, 5로 나누어 짐 (가운데 7을 더 쪼갤 수 있는지?)
(인자의 개수가 17일 때 뿐만 아니라 16일 때도 비슷한 문제가 발생함)
2.
인자가 18개가 주어질 경우 6, 6, 6으로 나누어 지는데 이걸 2,2,2,2,2,2,2,2,2로 나누어서 사용하면 비효율적이지 않을지?
