Subject
시간 복잡도와 점근 표기법 간단하게 이해하기
시간 복잡도와 점근 표기법 간단하게 이해하기
안녕하세요~ jchoi에요
오늘은 시간 복잡도와 점근 표기법에 대해 이야기해 볼게요!
알고리즘 분석에서는 주로 시간 복잡도에 관심을 두고, 이 알고리즘이 얼마나 좋은 성능을 내는지 (얼마나 빨리 답을 낼 수 있는지)를 생각합니다!
일반적으로 n (입력자료의 크기)에 비례해서 알고리즘은 연산시간이 증가(느려짐)하게 됩니다.
(입력 자료가 늘어날수록 빨라지는 알고리즘도 있나요..?? 제가 몰라서 혹시 있으면 댓글로 적어주세요!)
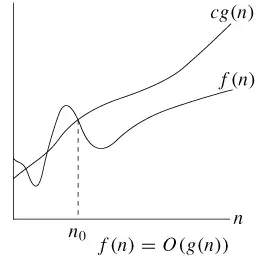
알고리즘 책에서 흔히 나오는 수학적 정의와 도표를 보자면!
보통 이런 기호 나오면 바로 내려버리신단 말이에요
그래서 제가 쉽게 써봤습니다
이렇게 할거였으면 팔만코딩경 안쓰고 그냥 링크 복붙하는게 낫죠!
1) 함수의 비교
무한끼리 비교하는 방법을 알아봅시다. 우선 점근표기법은, 시간 복잡도 함수로 표현된 f(n)에서 n을 무한으로 보내 비교하는건데 알아두셔야 할 점은 무한에도 급이 있다는 겁니다. 말하자면 무한끼리 대결을 시켜서 서열을 나누는 거죠
그럼 어떻게 비교를 하는가?
A : “난 무한이야”
B : “웃기시네! 난 더 무한이야!”
C: “난 더더무한이거든!”
(.. 이렇게 할리는 없겠져? ㅎㅎ.. 죄송합니다)
무한끼리의 이런 힘싸움?은 서로 나눈 식을 n을 무한으로 보냈을 때의 결과로 결정되는데요
그림을 봅시다!
이런 ‘양으로 발산하는 함수의’ 극한들의 힘싸움의 결과는 다음의 3가지입니다.
1.
0이거나(g가 더 셈)
2.
0이 아닌 상수거나 (비김)
3.
무한대로 발산하거나(f가더셈)
2) 발산하는 속도에도 급이 있다
아무튼 이런 비교질?을 통해 무한끼리의 레벨..? 계급?이 나눠집니다.
(여기서 ‘계급'은 수학 용어가 아니라 그냥 제가 설명할때 쓰는 말입니다. 오해마시길..)
같은 계급 안에서는 어떤 함수가 어떤 함수를 나눠서 극한을 취하더라도 0으로 수렴시키거나 무한정 발산시키지 못하고, 특정 값(=실수 상수)으로 수렴합니다. 같은 계급 간에도 뭐 힘쌘놈 있고 상대적으로 약한놈은 있지만 크게보면 비슷비슷 하다는것처럼, f(n) / g(n) 이 양수로 수렴해버리면 같은 수준으로 발산하는거에요
무한끼리의 이 계급은 굉장히 엄격해서 같은 계급에서 아무리 약한 녀석 (아무리 작은 함수)이라도 아래 계급의 최강자를 이깁니다.
•
함수 f(n) = n ^(0.000001)조차도 g(n) = (log n) ^ 42를 이긴다는 거에여, n이 발산한다면! (f(n)이 100만번 곱해져야 n과 같아집니다.)
•
실제로 로그는 무한중에 완전 호구인 편입니당..
(예를들어 밑이 10인 로그는, 1이 커지기 위해서 n = 1000000000에서 x의 양의 방향으로 자기 자신의 아홉배를 전진해야합니다)
“근데 내가(로그) 아무리 약해도 너(상수)는 이긴다 ㅋㅋㅋ”
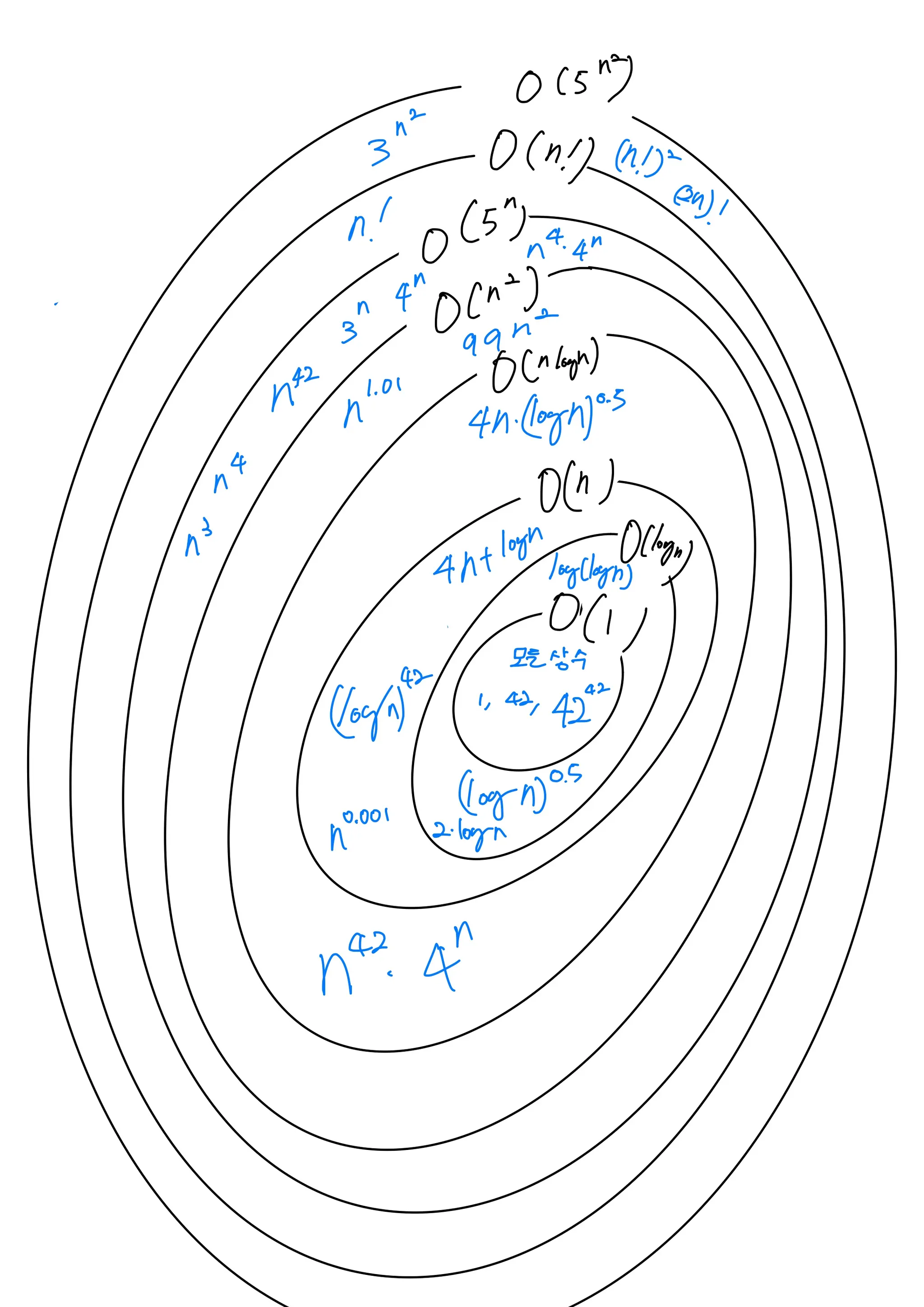
그럼 제가 열심히 그린 함수 계급표 예시를 보겠습니다!
제가 열심히 적어본 계급?표인데요, 파란색으로 적은건 그냥 대표값으로 제일 간단한 형식으로 적은것이고, ‘해당 수준의 발산속도를 가진 함수들의 집합’입니다. 오른쪽에 검정색으로 예시이자 그 집합의 원소들을 적어둔 것이죠.
그런데 왼쪽 파란색 기호를 보면 O(n) 처럼 ‘빅 오’(Big-O)가 아니라 Θ(n), ‘쎄타’(theta)로 적어 뒀습니다. 아직 빅 오에 대해서도 쎄타에 대해서도 설명을 안했으니까, 저 쎄타 기호는 대략 “괄호 안에 써있는 함수들이 n→∞ 무한대로 발산하는 같은 레벨, 같은 수준, 같은 계급을 가진” 그런 함수들이 속한 무리를 나타내는 기호로 봐 주세요!
•
Θ(n^2 + 1)은 Θ(4 * n^2) 과 정확히 똑같은 집합이에요, 저 괄호 안의 함수 n^2 + 1, 4 * n^2 이 모두 저 집합에 속하는거죠 저 표시는 가장 단순한 형태(최고차항만 남기고 계수를 1로 만든)로 표시한것일 뿐입니다!
각각의 도형들을 서로 떨어져있는 막대? 띠?같이 그려 뒀는데, 어떤 함수도 저 띠들에 동시에 속하지 못합니다. (쉽게 말해서, 저 띠들은 교집합이 없다는 뜻이에요) 위에 있을수록 더 빠르게 발산하고 아래에 있을수록 더 느리게 발산합니다. 위에 있는 놈들이 더 쎈놈들이고 같은 줄은 또이또이 하다는 거에여
같은 줄의 함수끼리는 나누고 극한을(n을 무한대로) 보내면 0보다 큰 양수로 수렴해요, 아랫 줄 함수로 윗줄 함수를 나누어 극한을 보내면 무한대로 뻗어나가고, 위에 줄 함수로 아랫줄 함수를 나누어 극한을 보내면 0으로 수렴합니다. 앞에서 함수 비교하는 방법 아직 생각나시죠?
저 막대들 사이사이에도 수많은 계급이 더 있습니다, 실수의 갯수가 무한하듯이, 0과 1 사이에 0.5가 있고 0.5와 1 사이에 0.75가 있고 0.75와 1 사이에 0.875가 있듯, 어떤것보다는 빠르게 발산하면서 어떤것보다는 느리게 발산하는 함수를 만들려면 계속 만들어 낼 수 있습니다.
3) 사실 ‘빅 오 어쩌구’는 집합이었습니다
f(n) = O(n) 이거는 생각하시는 그런 표현이 아닙니다.
나 = ‘42서울 카뎃’인데, 그렇다고 ‘42서울 카뎃' = 나 가 아니라는건 다들 아시죠..?
그러니까, ‘f(n) = O(g(n))’이라는 말은 원래
f(n) ∈ O(g(n)) 라는 뜻이었던 겁니당.. (그래서 거꾸로 쓰면 틀린 표현이 됩니다..)
그리고 대체 뭔 기호가 그렇게 많은지 어디선가 보기는 봤던것 같던
•
Θ(g(n)) [쎄타]
•
Ω(g(n)) [빅-오메가]
•
O(g(n)) [빅-오]
•
ω(g(n)) [스몰-오메가]
•
o(g(n)) [스몰 - 오]
얘네들 전부 다 집합입니다!
4) 그래서 빅 오가 뭐냐고
‘내밑으로 니위로 집합’(..?)으로 예를 들어보겠습니다,
1.
동 기수포함 내 위로 집합 : Ω(g(n)) [빅-오메가]
2.
동 기수포함 내 밑으로 집합 : O(g(n)) [빅-오]
3.
동기들 집합 : Θ(g(n)) [쎄타]
4.
동 기수빼고 내 위로 집합 : ω(g(n)) [스몰-오메가]
5.
동 기수빼고 내 밑으로 집합 : o(g(n)) [스몰 - 오]
Θ(g(n)) = Ω(g(n)) ∩ O(g(n))위의 ‘=’ 기호는 포함 기호를 대체한게 아니라 진짜로 동일한 집합이라는 뜻입니다. 그래서 어떤 알고리즘이 ‘어떤 정도의 시간 복잡도’를 갖는지를 표현하는 데에는 세타가 적절합니다.
‘빅-오' 는 ‘내 밑으로’ 의 의미라서 ‘이것보다 오래 걸리지는(=높은 수준의 발산정도를 갖지는) 않는다’ 라는 뜻이라서,O(1) ⊂ O(log n) ⊂ O(n) ⊂ O(n*log(n)) ⊂ O(n^2) ⊂ O(5^n) ⊂ O(n!)대충 빅 오 집합간에 이런 관계가 있거든요
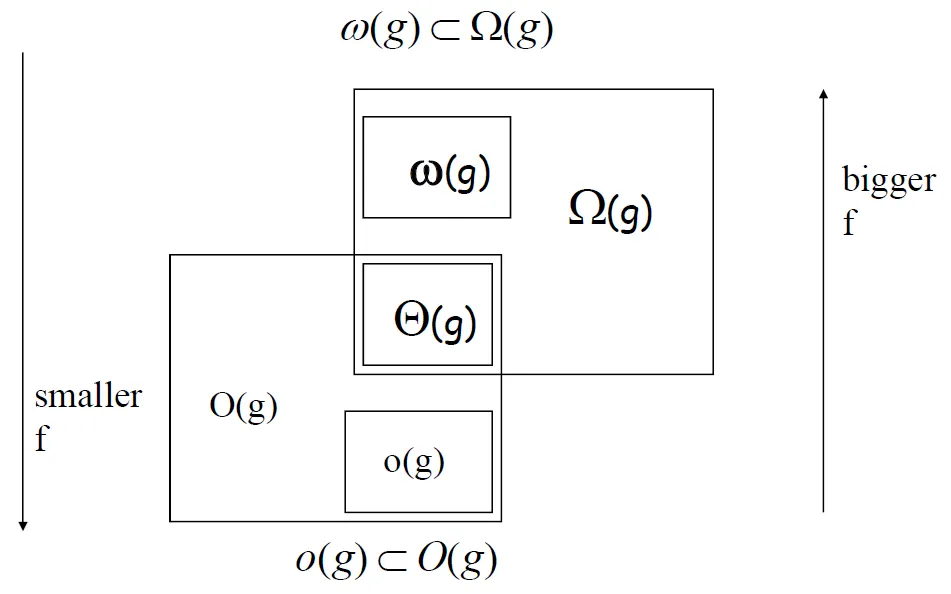
조금이라도 이해에 도움이 될까 한땀한땀 열심히 그렸습니다..!
스크롤을 올려서 계급표가 쎄타로 그려져 있던것들을 기억해 보세요!
아무튼!
•
동 기수포함 내 위로 집합 : Ω(g(n)) [빅-오메가]
•
동 기수포함 내 밑으로 집합 : O(g(n)) [빅-오]
•
동기들 집합 : Θ(g(n)) [쎄타]
•
동 기수빼고 내 위로 집합 : ω(g(n)) [스몰-오메가]
•
동 기수빼고 내 밑으로 집합 : o(g(n)) [스몰-오]
인터넷에서 얘들의 관계를 잘 설명하는 멋진 다이어그램을 찾았어요!
이번 문서에서는 점근 표기법의 의미를 배워보았어요!
다음에는 점화식에서 시간복잡도를 유도하는 방법을 알려드릴게요! 그럼 이만!