이름부터 클릭하기 싫어보이는..! 연쇄행렬 최소곱셈 알고리즘에 대해 공부해보자.
혹시 설명을 보지 않고 문제부터 풀어보고 싶은 분들은 여기서 먼저 문제를 풀어봐도 좋다.
이 글에서는 일단 문제부터 읽어 보고, 풀이에 필요한 개념을 설명한 뒤, 식을 세워 코드에 적용시켜 보는 순으로 진행하겠다.
 문제
문제
문제 설명
크기가 a by b인 행렬과 크기가 b by c 인 행렬이 있을 때, 두 행렬을 곱하기 위해서는 총 a x b x c 번 곱셈해야합니다.
예를 들어서 크기가 5 by 3인 행렬과 크기가 3 by 2인 행렬을 곱할때는 총 5 x 3 x 2 = 30번의 곱하기 연산을 해야 합니다.
행렬이 2개일 때는 연산 횟수가 일정 하지만, 행렬의 개수가 3개 이상일 때는 연산의 순서에 따라서 곱하기 연산의 횟수가 바뀔 수 있습니다. 예를 들어서 크기가 5 by 3인 행렬 A, 크기가 3 by 10인 행렬 B, 크기가 10 by 6인 행렬 C가 있을 때, 순서대로 A와 B를 먼저 곱하고, 그 결과에 C를 곱하면 A와 B행렬을 곱할 때 150번을, AB 에 C를 곱할 때 300번을 연산을 해서 총 450번의 곱하기 연산을 합니다. 하지만, B와 C를 먼저 곱한 다음 A 와 BC를 곱하면 180 + 90 = 270번 만에 연산이 끝납니다.
각 행렬의 크기 matrix_sizes 가 매개변수로 주어 질 때, 모든 행렬을 곱하기 위한 최소 곱셈 연산의 수를 return하는 solution 함수를 완성해 주세요.
제한 사항
•
행렬의 개수는 3이상 200이하의 자연수입니다.
•
각 행렬의 행과 열의 크기는 200이하의 자연수 입니다.
•
계산을 할 수 없는 행렬은 입력으로 주어지지 않습니다.
입출력 예
matrix_sizes | result |
[[5,3],[3,10],[10,6]] | 270 |
 개념
개념
연쇄행렬 최소곱셈 알고리즘은 말 그대로 연쇄적인 행렬의 곱셈을 할 때, 어떻게 결합해야 최소한의 곱셈 횟수로 계산할 수 있을지를 구하는 알고리즘이다. 이 알고리즘에 대한 본격적인 설명에 앞서, 먼저 알고가야 할 개념들이 있다.
행렬의 곱셈
간단한 행렬의 곱을 예로 들어보면 다음과 같다.
오늘 배울 알고리즘에서는 각각의 값은 중요하지 않다. 각 행의 열의 크기가 어떻게 변하고, 총 몇 번의 곱셈이 필요한지가 중요하다.
2 by 2 행렬과 2 by 3 행렬을 곱하면 2 by 3 행렬이 되는데, 이 때 필요한 곱셈 연산의 수는 2*2*3=12 번이다.
그러니까, a by b 행렬과 b by c 행렬을 곱하면 a by c 행렬이 되고, 곱셈 연산 수는 a * b * c 번이다.
여기서 한가지 주의해야할 점은 행렬의 곱에서 b의 크기가 동일해야 한다는 것이다.
이걸 바탕으로 연쇄행렬의 최소 곱셈 수는 어떻게 구하는지 이제 차근차근 알아가 보겠다.
연쇄행렬 곱셈의 결합 형태
연쇄행렬 최소곱셈 알고리즘은 말 그대로 연속적인 여러 행렬을 곱할 때, 필요한 곱셈의 최소 연산 횟수를 찾는 알고리즘이다.
행렬을 연쇄적으로 곱해야 할 때, 어떤 행렬을 먼저 곱 하느냐에 따라 필요한 연산 횟수도 달라진다.
다음과같이 A, B, C, D, E 다섯 개의 행렬이 있을 때, 결합 순서에 따라 달라 지는 연산 횟수를 확인할 수 있다.
Source님의 티스토리에서 다섯 개의 행렬을 곱할 때, 가장 마지막에 계산하게 되는 결합의 형태를 네 개로 분류해 주었다.
다섯 개의 행렬일 때는 항상 4가지의 경우의 수가, n개일 때는 항상 n - 1가지의 경우의 수가 존재한다.
예를 들어, ((AB)C)(DE)는 A와 B를 먼저 곱하고, AB에 C를 곱하고, D와 E를 곱하고… 마지막으로 ABC와 DE를 곱해서 type 2의 경우가 되는 것이다. (((A(BC))D)E)는 결국 ABCD와 E의 곱이므로 type 4의 경우가 된다.
이 시점에서 다시 문제를 보자. 우리는 최대 200개의 행렬에 대해 최소 곱셈 수를 구해야 한다. 모든 경우의 수를 탐색 하려면 효율성 부분에서 실패하게 되므로, 다이나믹 프로그래밍으로 풀이를 진행한다.
 문제 풀이
문제 풀이
점화식 만들기
위에서 5개의 행렬을 ((AB)C)(DE) 로 나눌 때, 각 결합은 ((AB)C)와 (DE)로 나뉜다. 결합 들은 더 작은 개수의 결합으로 이루어져 있으므로 여기서 슬금슬금 점화식의 실마리가 보이게 된다.
DP 배열 M[i][j]를 먼저 정의할 텐데, 이는 여느 다이나믹 프로그래밍 풀이법과 마찬가지로 구해야 하는 값을 고려해서 정의한다.
우리는 최종적으로, matrix_sizes의 첫번째 부터 끝번째행렬 까지를 모두 곱 했을 때의 최소 곱셈 연산 횟수가 필요하다.
dp[i][j] : matrix_sizes의 i번째 행렬부터 j번째 행렬까지 곱했을 때의 최소 곱셈 연산 횟수
M[i][i]는 무조건 0이다. 행렬이 하나면 연산은 일어나지 않는다.
점화
이제 i = 1, j = 1부터 시작해보자. 식에서 사용한 변수의 설명은 다음과 같다.
◦
k: i부터 j - 1까지 순회하면서 결합의 위치를 나누어주는 변수이다. 위에 든 예시인 ((AB)C)(DE) 에서 k는 3이다.
◦
: by 행렬과 by 행렬의 곱셈 연산 횟수 이다.
•
i = 1, j = 1
◦
i == j 일 때는 0이므로, M[1][1]도 0이다.
•
i = 1, j = 2
◦
두 개의 행렬을 곱하는 경우이다. M[1][1]과 M[2][2]는 0이므로, 결국 만 계산하면 된다.
◦
M[2][3], M[3][4] 등 두 개의 행렬을 곱하는 경우도 같은 방법으로 계산한다.
•
i = 1, j = 3
◦
세 개의 행렬을 곱하는 경우이다. (A(BC)), ((AB)C) 두 가지 경우 중에 더 적은 연산을 M[1][3]에 쓰면 된다.
◦
M[1][1], M[2][3], M[1][2], M[3][3]모두 이미 계산이 가능한 값이므로 구할 수 있다.
•
i = 1, j = 4
◦
네 개의 행렬을 곱하는 경우이다. (A(BCD)), ((AB)(CD)), ((ABC)D) 세 가지 경우 중에 더 적은 연산을 M[1][3]에 쓰면 된다.
짜잔
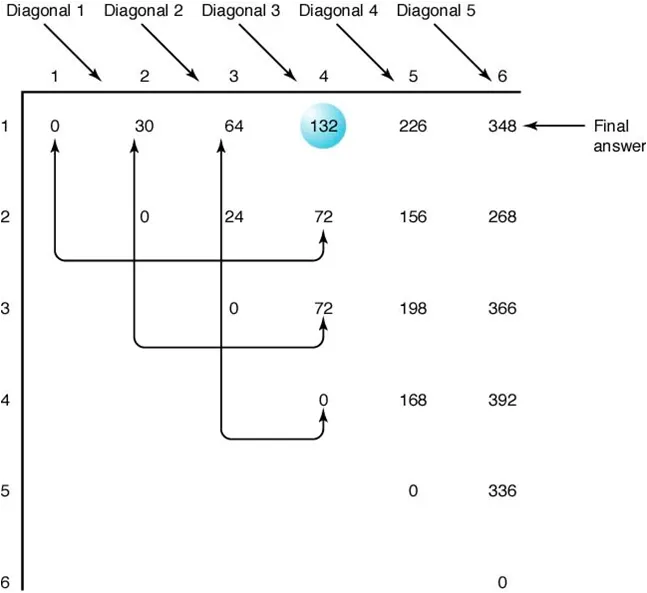
그래서 위의 과정을 거치다 보면 점화식을 구할 수 있다. 배열의 예시를 그림으로 나타낸 게 있어 이해에 도움이 되었음 해서 첨부한다.
왼쪽의 이 예시는
A1 (5 by 2)
A2 (2 by 3)
A3 (3 by 4)
A4 (4 by 6)
A5 (6 by 7)
A6 (7 by 8)
의 연쇄행렬 곱셈을 계산한 그림이다.
대각선의 i == j 인 경우를 0으로 놓고, 오른쪽 위 대각선 한줄씩 계산해 나가는.. 점화식인 것이다.
코드 짜기
이제 위의 점화식을 토대로 코드를 짜보자 (여기까지 정말 한참 걸렸다..)
먼저 벡터를 선언하고, 우리는 최소값을 기록해야 하므로 최대값으로 초기화 해준다.
(999999999 대신 climits 헤더의 INT_MAX 같은 값으로 했으면 더 보기 좋았을지도 모르겠다.)
vector<vector<int>> dp(matrix_sizes.size(), vector<int>(matrix_sizes.size(), 999999999));
C++
복사
그리고 i == j 인 경우의 배열을 0으로 세팅해준다.
for (int i = 0; i < matrix_sizes.size(); i++)
dp[i][i] = 0;
C++
복사
이제 행렬을 순회하면서 값을 채워준다. 대각선 기준으로 절반만 순회하면 되므로, j는 matrix_sizes.size() - i 만큼만 돌아주면 된다.
// dp[a][b] : a번째 ~ b번째 행렬들을 다 곱했을 때 최소 연산 수
// dp[a][b] = [(a) ~ (k) 연산 수] + [(k + 1) ~ (b) 연산 수] + [그 두 연산의 결과로 나온 행렬의 연산 수]
// a * k * b => (tmp[a[0]][k[1]]의 행렬) * b => (res[a[0]][b[1]]의 행렬)이 됨
int a, b;
for (int i = 0; i < matrix_sizes.size(); i++) {
for (int j = 0; j < matrix_sizes.size() - i; j++) {
if (j == j + i)
continue;
a = j;
b = j + i;
for (int k = a; k < b; k++)
dp[a][b] = min(dp[a][b],
dp[a][k] + dp[k + 1][b]
+ matrix_sizes[a][0] * matrix_sizes[k][1] * matrix_sizes[b][1]);
}
}
C++
복사
우리가 구하려 했던 값은 첫번째 부터 끝번째 까지를 모두 곱 했을 때의 최소 곱셈 연산 횟수, dp[0][matrix_sizes.size() - 1]이다.
문제에서 행렬의 개수는 3개 이상이고, 계산할 수 없는 경우의 행렬은 주어지지 않으므로 예외 없이 바로 리턴하면 된다.
return dp[0][size - 1];
C++
복사
최종 코드
#include <vector>
using namespace std;
int solution(vector<vector<int>> matrix_sizes) {
int size = matrix_sizes.size();
vector<vector<int>> dp(size, vector<int>(size, 999999999));
for (int i = 0; i < size; i++)
dp[i][i] = 0;
int a, b;
for (int i = 0; i < size; i++) {
for (int j = 0; j < size - i; j++) {
if (j == j + i)
continue;
a = j;
b = j + i;
for (int k = a; k < b; k++)
dp[a][b] = min(dp[a][b],
dp[a][k] + dp[k + 1][b]
+ matrix_sizes[a][0] * matrix_sizes[k][1] * matrix_sizes[b][1]);
}
}
return dp[0][size - 1];
}
C++
복사