Search
Duplicate
🌀

[fract-ol] fractal 개념

간단소개
팔만코딩경 컨트리뷰터
ContributorNotionAccount
주제 / 분류
42seoul
Scrap
태그
9 more properties

프랙탈(Fractal)

개념

일부 작은 조각이 전체와 비슷한 기하학적인 형태.
재귀적이거나 반복적인 작업에 의한 패턴으로 만들어진다.
•
프랙탈 구조: 자기유사성을 갖는 기하학적인 구조
자기유사성(self-similarity): 부분을 확대할 때 자기가 포함된 전체와 닮은 모습을 보여 주는 성질

분류

생성 기법

•
Escape-time
◦
시간 매개형 프랙탈, 궤도 프랙탈
◦
복소평면상에서 각가의 점이 발산하는 속도를 색으로 나타낸 이미지
◦
ex) 망델브로 집합
•
Iterated function system
◦
반복 함수계
◦
기하학적 대체규칙에 의해 만들어진 도형
◦
ex) 칸토에 집합, 시에르핀스키 삼각형, 시에르핀스키 카펫, 코흐 곡선, 피아노 곡선
•
Strange attractors
◦
기이한 끌개
◦
주어진 사상이나 방정식의 해를 이용해 초기값을 반복적으로 변환한 것
•
Random
◦
무작위적 프랙탈

자기유사성 강도

•
준 자기유사적
◦
통계학적 프랙탈
◦
자기유사성의 강도가 가장 낮음
◦
자연에서 찾은 프랙탈 처럼 부분과 전체가 대략적으로 비슷한 프랙탈
•
완전 자기유사적
◦
규칙적 프랙탈
◦
자기유사성의 강도가 가장 높음
◦
부분과 전체의 모양이 정확하게 같다
◦
ex) 시에르핀스키 삼각형, 코흐 곡선, ...

종류

망델브로 집합(Mandelbrot set)

점화식

Zn+1=Zn2+CZ_{n+1} = Z_n^2+C (Z, C는 복소수)
M={C:Zn+1=Zn2+C,lim⁡n→∞∣Zn∣<∞}M = \{C: Z_{n+1} = Z_n^2+C, \lim\limits_{n\to\infty}\left\vert Z_n\right\vert<\infty\}
무한으로 계산할 수 없기 때문에 실용적으로는 lim⁡n→∞∣Zn∣<2\lim\limits_{n\to\infty}\left\vert Z_n\right\vert<2 로 한다

개념

정해진 Z의 초기값에 대해 점화식을 수렴시키는 C의 집합
특정 C값에서는 ZnZ_n의 값이 계속 증가하지만, 또 다른 C값에서는 ZnZ_n이 아주 작은 두 허수 사이를 왕복 함.

예시

M={C:Zn+1=Zn2+C,lim⁡n→∞∣Zn∣<2}M = \{C: Z_{n+1} = Z_n^2+C, \lim\limits_{n\to\infty}\left\vert Z_n\right\vert<2\}
1.
C=0C = 0
Z0=C=0Z_0 = C = 0
Z1=Z02+C=02+0=0Z_1=Z_0^2+C=0^2+0=0
Z2=Z12+C=02+0=0Z_2=Z_1^2+C=0^2+0=0
...
→
lim⁡n→∞∣Zn∣=0<∞\lim\limits_{n\to\infty}\left\vert Z_n\right\vert =0 < \infty
∴0∈M\therefore0\in M
2.
C=1C = 1
Z0=C=1Z_0 = C = 1
Z1=Z02+C=12+1=2Z_1=Z_0^2+C=1^2+1=2
Z2=Z12+C=22+1=5Z_2=Z_1^2+C=2^2+1=5
...
→
lim⁡n→∞∣Zn∣=∞\lim\limits_{n\to\infty}\left\vert Z_n\right\vert = \infty
∴1∉M\therefore1\notin M
3.
C=−1C = -1
Z0=C=−1Z_0 = C = -1
Z1=Z02+C=(−1)2−1=0Z_1=Z_0^2+C=(-1)^2-1=0
Z2=Z12+C=02−1=−1Z_2=Z_1^2+C=0^2-1=-1
...
→
lim⁡n→∞∣Zn∣={0−1<∞\lim\limits_{n\to\infty}\left\vert Z_n\right\vert = \begin{cases}0 \\ -1\end{cases} < \infty
∴−1∈M\therefore-1\in M

줄리아 집합 (Julia set)

점화식

Zn+1=Zn2+CZ_{n+1} = Z_n^2+C (Z, C는 복소수)
M={Z:Zn+1=Zn2+C,lim⁡n→∞∣Zn∣<∞}M = \{Z: Z_{n+1} = Z_n^2+C, \lim\limits_{n\to\infty}\left\vert Z_n\right\vert<\infty\}

개념

정해진 C에 대해 점화식을 수렴시키는 Z의 집합
발산, 수렴이 초기값 Z에 의해 결정된다

예시

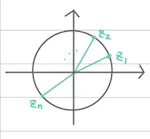
Zn+1=Zn2Z_{n+1} = Z_n^2
1.
∣Zn∣=1\left\vert Z_n\right\vert = 1
ZnZ_n값은 반지름이 1인 원을 따라 움직임
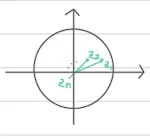
2.
0<∣Zn∣<10 < \left\vert Z_n\right\vert < 1
ZnZ_n값이 점점 작아짐
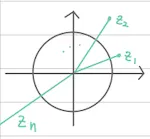
3.
∣Zn∣>1\left\vert Z_n\right\vert > 1
ZnZ_n값이 점점 커짐
∴∣Zn∣=1\therefore\left\vert Z_n\right\vert = 1을 기준으로 수렴하는 영역과 발산하는 영역이 구분 됨.
|Zn| = 1 을 기준으로 영역이 구분 된 줄리아 집합 모습
Zn+1=Zn2Z_{n+1} = Z_n^2 의 결과는 간단하지만 C를 더하게 되면 복잡한 양상이 나타남.
c값 변화에 따른 julia집합 모양 변화
참고한 사이트
•
•
위키백과-망델브로 집합: https://ko.wikipedia.org/wiki/망델브로_집합
•
위키백과-줄리아 집합: https://en.wikipedia.org/wiki/Julia_set
Made with