Search
Duplicate
🧐

JavaScript에서 표현할 수 있는 수의 범위와 부동소수점

간단소개
JavaScript에서 표현할 수 있는 수(Number)의 범위를 부동 소수점 표현 방식으로 계산해보며, 더 나아가 C언어의 double 타입의 유효자릿수가 16인 이유를 알아보자.
ContributorNotionAccount
주제 / 분류
Javascript
IEEE
잡지식
태그
minmax
etc
IEEE 754
Scrap
팔만코딩경 컨트리뷰터 (Library DB (속성)에 관계됨)에 관계됨
7 more properties
대부분의 프로그래밍 언어가 그러하듯이 JavaScript 또한 표현할 수 있는 숫자(Number)의 범위가 정해져있다.
JavaScript에서 표현할 수 있는 수의 범위를 직접 계산해보기 위해서 공부를 시작했지만, 이때 이 도전을 멈췄어야 했다.
STAY..
※ 참고로 팔만코딩경에는 이미 부동소수점에 대해서 잘 정리된 글들이 많기 때문에
이 글은 부동소수점에 대해 알고 있다는 전제하에 작성되었습니다.
JavaScript에서 표현할 수 있는 수의 범위를 부동 소수점 표현 방식을 통해 계산해보는게 이 글의 목표입니다.

문제의 시작

JavaScript가 최대 혹은 최소로 표현할 수 있는 수의 범위는 아래와 같다.
console.log(Number.MAX_VALUE); //1.7976931348623157e+308 (최댓값) console.log(Number.MIN_VALUE); //5e-324 (최솟값)
JavaScript
복사
이 값을 넘어가면 Infinity로 인식하거나 값이 파괴되어 정확한 값이 나오지 않는다.
궁금했던 것은 “표현할 수 있는 수의 범위가 어떻게 정해졌는가”였다.
1.7976931348623157e+308 1.7976931348623157e+308 과 5e−3245e-324가 어떻게 나온 숫자인지 꼭 계산해보고 싶었다.

결론

결론 먼저 말하자면, 이러한 결과가 나오는 이유는 JavaScript가 double-precision 64-bit 형식으로 수를 표현하기 때문이다.
즉, JavaScript에서 표현하는 수는 배정밀도 부동 소수점 수(double precision floating point numbers)로 표현할 수 있기 때문이다.

풀이과정1. 부동 소수점

64비트 부동 소수점을 직접 계산해보기 전에 부동 소수점(floating-point)에 대해서 알아야 한다.
부동 소수점은 간단하게 말해서, 컴퓨터에서 소수점이 포함된 실수를 표현하기 위한 방식 중 하나이다. 더 자세한 사항은 많은 부동소수점에 대한 글들을 찾아보면 될 것 같다.
부동소수점 연산의 공식적인 표준은 IEEE 754-2019이며,
표준 문서는 아래의 IEEE 정식 사이트에서 구매(유료)해서 볼 수 있다.
다만, 부동 소수점에 대한 전문 지식이 필요한게 아니라면 잘 구매하지 않는다.
754-2019 - IEEE Standard for Floating-Point Arithmetic
This standard specifies interchange and arithmetic formats and methods for binary and decimal floating-point arithmetic in computer programming environments. This standard specifies exception conditions and their default handling. An implementation of a floating-point system conforming to this standard may be realized entirely in software, entirely in hardware, or in any combination of software and hardware.
https://ieeexplore.ieee.org/document/8766229

풀이과정2. double precision floating point numbers?

JavaScript가 숫자를 표현하는 형식은 double precision floating point이다.
IEEE754 표준에 따르면 부동 소수점 수(floating-point numbers)는 두 가지 방식으로 표현될 수 있다.
1.
single precision (단정밀도) ► 부동 소수점 수를 32비트(4바이트)로 나타낸다. ► 지수부는 8비트(1바이트)를 사용한다. ► 가수부는 23비트(3바이트)를 사용한다. ► bias 번호는 127이다. ► 표현 가능한 범위는 대략 2−1262^{-126} 부터 21272^{127} 까지이다. ► 정밀도(precision)가 덜 중요한 경우에 사용된다. ► binary32라고도 한다.
2.
double precision (배정밀도) ► 부동 소수점 수를 64비트(8바이트)로 나타낸다. ► 지수부는 11비트를 사용한다. ► 가수부는 52비트를 사용한다. ► bias 번호는 1023이다. ► 표현 가능한 범위는 대략 2−10222^{-1022} 부터 210232^{1023} 까지이다. ► single precision보다 더 정밀도(precision)가 중요한 경우에 사용된다. ► binary64라고도 한다.
(출처 : geeksforgeeks)
C언어의 자료형을 기준으로 봤을 때,
single precision은 float형, double precision은 double형이라고 할 수 있다.
JavaScript는 C언어의 double 자료형과 같이 64비트로 부동 소수점 수를 표현하는 double precision 방식으로 수(Number)를 표현한다.

풀이과정3. JavaScript에서 숫자(Number)는 몇 개?

► 64비트 부동 소수점으로 표현할 수 있는 숫자는 총 2642^{64}개이다. 64개의 비트가 있고, 각 비트에는 0 또는 1이 들어가게 되기 때문에 모든 경우의 수를 구하면 2642^{64}개가 된다.
► NaN(Not-a-Number)으로 표현되는 숫자는 총 2532^{53}개이다. 이를 이해하기 위해서는 위키백과의 도움을 좀 받아야 한다.
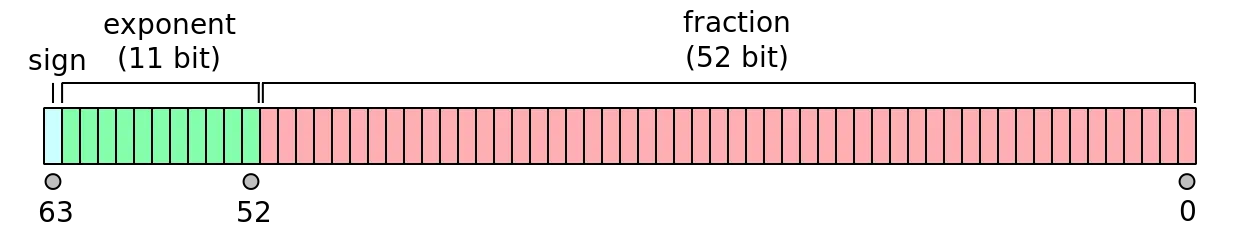
그림 출처 : 위키백과
위의 그림은 부동 소수점으로 표현하는 방법이며, 각 비트에는 0 혹은 1이 들어간다.
부동 소수점으로 표현하기 전에 정규화 과정을 거쳐야 하는데, 공식은 다음과 같다.
number=(−1)sign∗(1+Fraction)∗2exponent−Biasnumber = (-1)^{sign} * (1+Fraction) * 2^{exponent-Bias}
※ 자세한 사항은 부동 소수점 표현 방식에 대해서 별도로 공부하는 것을 추천
IEEE754 표준에 따라 지수(exponent)가 00000000001200000000001_{2} 일 때는, 가장 작은 지수를 구할 수 있다.
2exponent−Bias=21−1023=2−10222^{exponent-Bias} = 2^{1-1023} = 2^{-1022}
반대로 exponent가 11111111110211111111110_{2} 이면 가장 큰 지수를 구할 수 있다.
2exponent−Bias=22046−1023=210232^{exponent-Bias} = 2^{2046-1023} = 2^{1023}
이는 [풀이2]에서 언급한 double precision의 특징 중 하나인 “표현 가능한 범위”이기도 하다.
※ 유의사항
한가지 더 알아둬야 할 사항은 지수(exponent)가 00000000000200000000000_{2}일 때와 11111111111211111111111_{2}일 때의 경우이다.
IEEE754 표준에 의하면 이 값들은 다음과 같이 특별한 값으로 정의되어 있다고 한다.
•
지수(exponent)가 00000000000200000000000_{2} 이고 가수(fraction)가 모두 00 일 때 → 0(zero)를 나타내는데 사용한다. → 부호에 따라 +0이 될 수도 있고 -0이 될 수도 있다.
•
지수(exponent)가 11111111111211111111111_{2}일 때 → Infinity혹은 NaN을 나타내는데 사용한다. → 가수(fraction)에는 0 혹은 1이 채워진다.
만약, Infinity 혹은 NaN으로 표현되는 값의 개수를 구해야 한다면
부동 소수점 방식으로 표현 했을 때 지수(exponent)부 비트는 1111111111111111111111이 되고, 가수(fraction)부의 각 비트가 0 혹은 1로 채워지는 모든 경우의 수를 구하면 된다. (2532^{53}개)

풀이과정4. 부동 소수점의 정규화된 수와 비정규화된 수

이제 정규화(Normalization)와 비정규화(Denormalization)에 대해서 알아야 한다.
[풀이2]에서 언급한 특별한 값, “NaN, Infinity ”을 제외하면
JavaScript가 표현할 수 있는 유한한 수(finite numbers)의 개수는 264−2532^{64}-2^{53}개이다.
여기에서 부호가 있는 0(zero)인 +0와 -0까지 제외하면 나머지 유한한 수는 264−253−22^{64}-2^{53} - 2개가 된다.
이 유한한 수들(finite numbers)은 IEEE754 표준에 따라
정규화(Normalization)된 형태와 비정규화(Denormalization)된 형태로 표현될 수 있다.
[풀이2]에서는 정규화만 언급하고 비정규화를 언급하지 않았지만, 사실 두 가지의 형태로 표현된다.
•
정규화된 수(normalized numbers)
쉽게 말해서 소수점 위의 첫번째 숫자(유효 숫자)가 1만 남도록 하는 것이다.
만약 0.6250.625라는 10진법으로 표현된 값을 정규화 한다면,
0.625=0.101(2)=1.01(2)∗2−10.625 = 0.101_{(2)} = 1.01_{(2)} * 2^{-1}가 된다.
이때 정규화된 수는 1.01(2)∗2−11.01_{(2)} * 2^{-1}이다.
•
비정규화된 수(denormalized numbers)
→ 비정규화된 값은 정규화할 수 없는 작은 수를 말한다.
→ 보통 0에 가까운 값을 나타내기 위해서 사용한다. (0은 비정규화된 수가 아니다)
→ 지수(exponent)의 비트는 모두 00이 되며, 가수(fraction)의 각 비트에는 0 또는 1이 들어간다.
→ 비정규화된 수를 사용하는 동작을 ‘점진적 언더플로우’라고 한다.
예를 들어서, 1.01(2)∗2−10251.01_{(2)} * 2^{-1025}라는 값이 있다고 가정하면,
이 값은 소수점 위의 유효숫자가 1이 되도록 하는 정규화된 값으로 변환할 수가 없다.
정규화 가능한 수의 범위(1.01(2)∗2−10221.01_{(2)} * 2^{-1022}~1.01(2)∗210231.01_{(2)} * 2^{1023})보다 훨씬 작은 수이기 때문이다.
1.01∗2−1025=1.01∗2−3∗2−1022=0.00101∗2−10221.01 * 2^{-1025} = 1.01 * 2^{-3} * 2^{-1022} = 0.00101 * 2^{-1022}
이때 소수점 위의 첫번째 숫자(유효숫자)가 1이 아닌 0이 올 수 있도록 할 수 있는데,
이를 비정규화된 수라고 한다.
비정규화된 수(denormalized numbers)도 부동 소수점 방식으로 표현될 수 있다.
지수(exponent)부의 비트는 모두 00으로 표현하며, 가수(fraction)부에는 0 또는 1이 들어간다.
비정규화된 수로 표현할 수 있는 최댓값은 0.1111...(2)∗21−10230.1111..._{(2)} * 2^{1-1023}이다.

풀이과정5. JavaScript에서 표현할 수 있는 수의 범위

이제 정말 모든 준비가 끝났다. JavaScript에서 표현할 수 있는 수의 범위를 직접 구해볼 수 있다.
즉, 64비트 부동 소수점으로 표현할 수 있는 수의 범위를 구할 수 있다.
•
정규화된 부동소수점
일단 정규화 과정을 거친 수를 부동 소수점 방식으로 표현 한다고 했을 때,
표현할 수 있는 숫자의 개수는 총 264−2542^{64}-2^{54}이다.
그림 출처 : 위키백과
•
[풀이3]에서 말한대로 지수(exponent)가 모두 1인 경우(11111111111211111111111_{2})는 제외되고,
•
[풀이4]에 의해서 +0과 -0이 제외되며,
•
[풀이4]에 의해서 비정규화된 수가 제외되었다.
정규화된 수가 부동 소수점 방식으로 표현되면, 각 비트에 들어가는 값은 다음과 같다.
•
부호(sign)는 1 또는 (-1)이 되며
•
지수(exponent) 영역에는 0000000000100000000001 부터 1111111111011111111110 까지의 비트가 들어가며
•
가수(fraction)의 52비트에는 0 또는 1이 각 자리에 들어간다.
양의 숫자(정수, 실수)를 기준으로 부동 소수점으로 표현할 수 있는 수의(=64비트 부동 소수점 방식을 사용하는 컴퓨터가 표현할 수 있는 수의) 최솟값을 구해보면 다음과 같다.
보기 편하게 지수부와 가수부로 나눠서 표현했다.
※ 여기에서 말하는 최솟값은 정규화된 수 중 가장 작은 값이다. (JS가 표현할 수 있는 가장 작은 수 X)
지수부 : 00000000001 (총 11비트) 가수부 : 0000000000000...(중략)...01 (총 52비트)
JavaScript
복사
이 값을 정규화된 형식으로 표현해보면 다음과 같다.
(1+0.0000...1)(2)∗21−1023=(1+0.0000...1)(2)∗2−1022(1+0.0000...1)_{(2)} * 2^{1-1023} = (1+0.0000...1)_{(2)} * 2^{-1022}
10진법으로 표현하면 대략 2.225073858507202e−3082.225073858507202e-308정도이다.
이 숫자가 정규화된 부동소수점 수 중에서 가장 작은 양의 숫자이다.
최댓값을 구하는 것도 어렵지 않다. 지수가 커지면 된다.
지수부 : 11111111110 (총 11비트) 가수부 : 1111111111111...(중략)...11 (총 52비트)
JavaScript
복사
(1+0.11111...)(2)∗22046−1023=(1+0.11111...)(2)∗21023(1+0.11111...)_{(2)} * 2^{2046-1023} = (1 + 0.11111...)_{(2)} * 2^{1023}
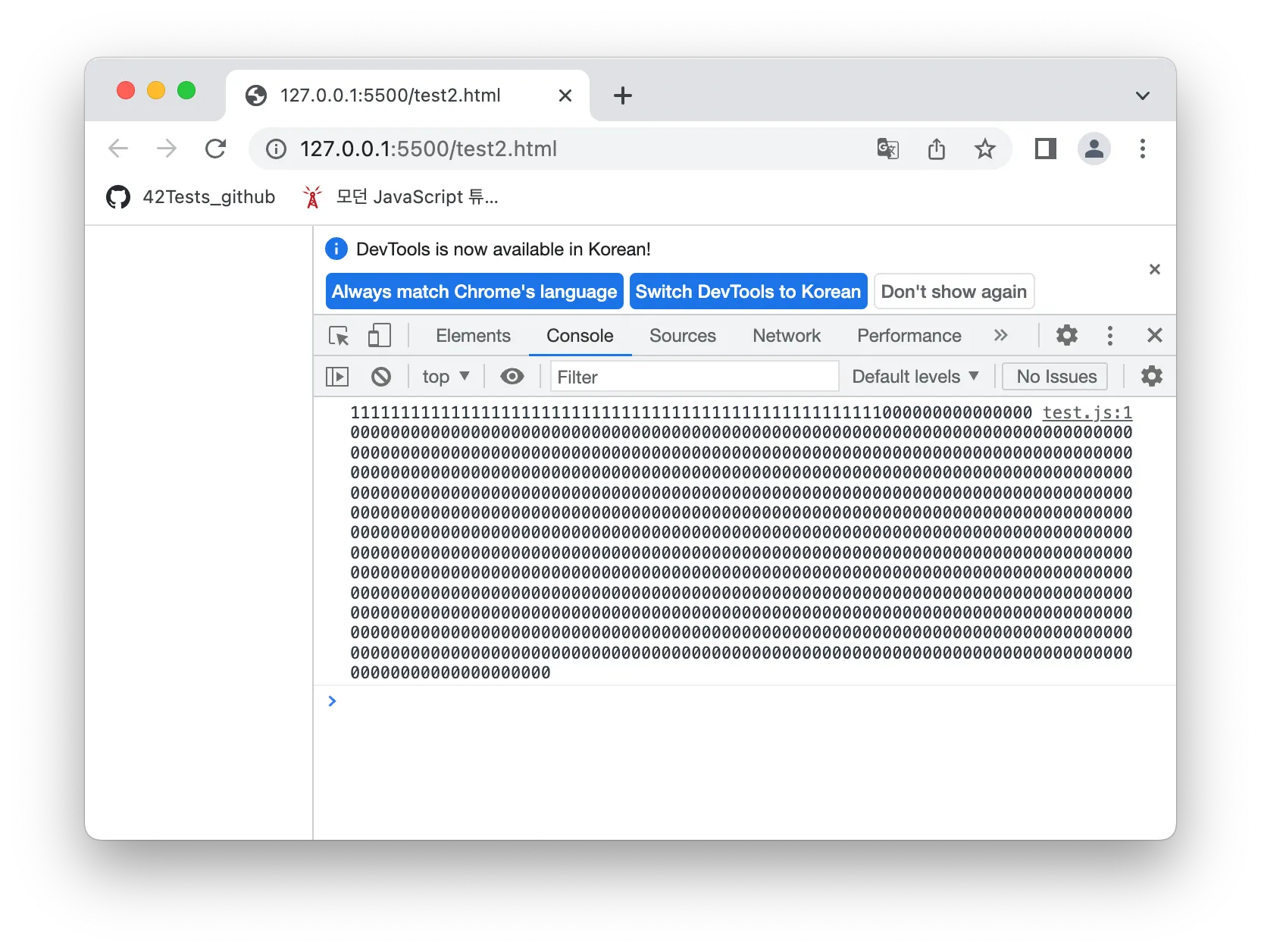
이 값을 10진법으로 변환하면 1.7976931348623157e+3081.7976931348623157e+308 정도가 된다.
JavaScript가 표현할 수 있는 제일 큰 양의 숫자 값을 Number.MAX.VALUE로 확인할 수 있는데,
2진법의 문자열로 출력해서 직접 확인해볼 수도 있다.
•
비정규화된 부동 소수점
비정규화된 수를 부동 소수점 방식으로 표현할 수도 있다.
[풀이3]에서 JavaScript가 표현할 수 있는 유한한 수(finite numbers)의 개수는 총 264−253−22^{64}-2^{53} - 2이라고 했는데, 이 중 254−22^{54}-2개가 비정규화된 값이다.
정규화된 수를 부동 소수점으로 표현했을 때, 부동 소수점 방식으로 표현할 수 있는 범위(=컴퓨터가 표현할 수 있는 수의 범위)를 구했던 것처럼
비정규화된 수 또한 표현 가능한 숫자의 범위를 구할 수 있다.
[풀이3]에서도 언급한 것과 같이 비정규화된 수는 0에 가까운 수를 나타내기 위해 사용되며,
여기에서 계산된 최솟값이 JavaScript가 표현할 수 있는 수의 최솟값이 된다.
지수부 : 00000000000 (총 11비트) 가수부 : 00000000000000...(중략)...01 (총 52비트)
JavaScript
복사
(0+0.00000...1)(2)∗21−1023=(0.00000...1)(2)∗2−1022(0+0.00000...1)_{(2)} * 2^{1-1023} = (0.00000...1)_{(2)} * 2^{-1022}
10진법으로 변환해보면 대략 5e−3245e-324가 된다.
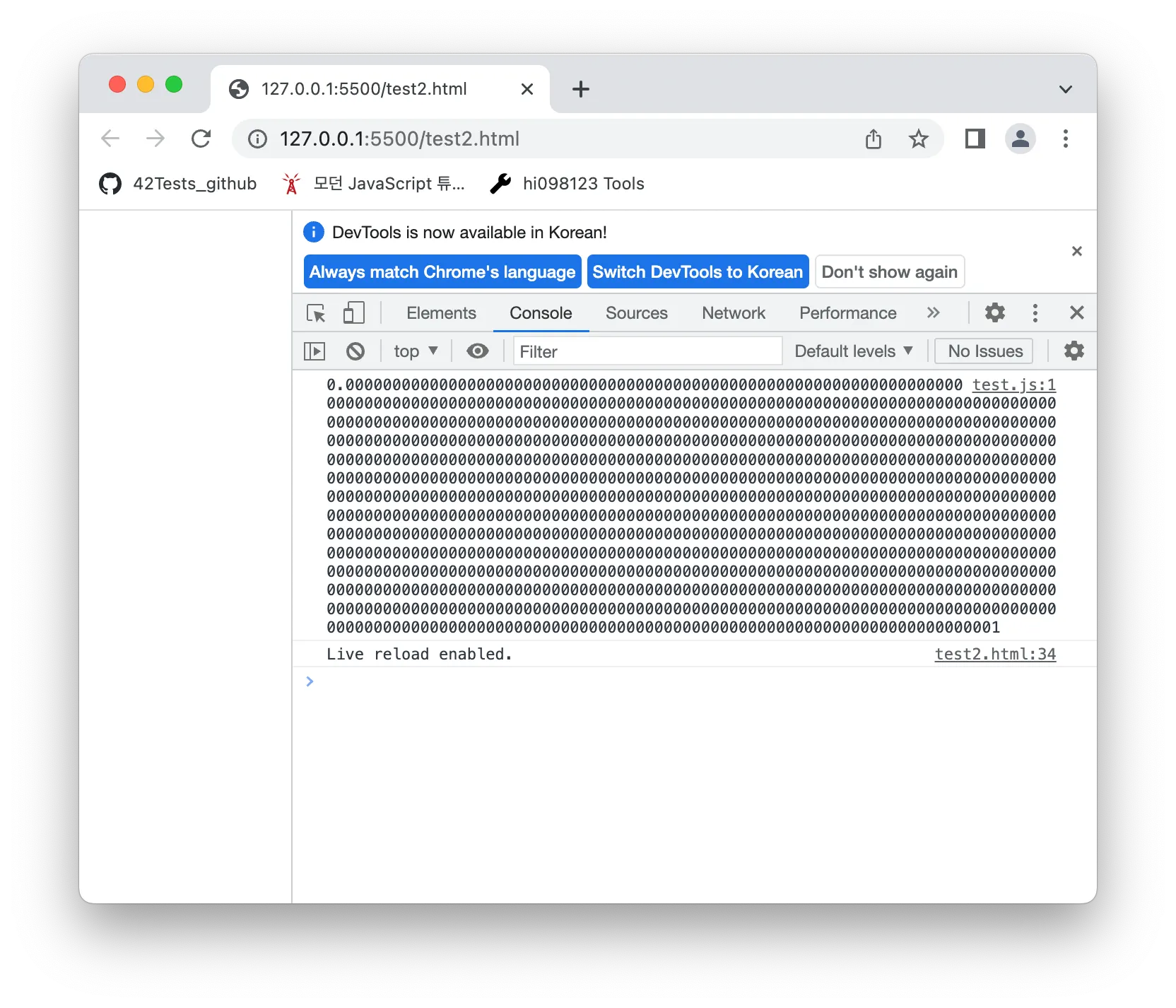
JavaScript가 표현할 수 있는 제일 작은 양의 숫자 값을 Number.MIN.VALUE로 확인할 수 있는데, 2진법의 문자열로 출력해서 확인해보면 소수점 아래로 1074자리의 수가 표현되는 것을 알 수 있다.
따라서 JavaScript는 양의 수(정수, 실수)를 기준으로 했을 때,
5e−3245e-324부터 1.7976931348623157e+3081.7976931348623157e+308까지의 수를 표현할 수 있다.

끝

ECMA-262 명세에 따르면 모든 유한한 양수는 동일한 크기를 가진 음수와 대응된다고 되어있다.
+1이 있으면, -1도 있는 것이고 +2022가 있으면, -2022도 있다는 의미이다.
따라서, 위에서 양의 숫자(정수, 실수)를 기준으로 최솟값과 최댓값을 구했지만
음수도 동일하게 대응되기 때문에 부호만 바꾸면 음의 숫자(정수, 실수)에서의 최솟값과 최댓값을 구할 수 있다.
참고로, C언어의 double형 또한 배정밀도 부동 소수점 형식(double-precision floating point format)으로 값을 표현하기 때문에
[풀이5]의 과정을 잘 이해하면 “double형이 표현(저장) 가능한 값의 범위”가 왜 약 −1.7e308-1.7e308 부터 1.7e3081.7e308까지인지 알 수 있다.

번외. C언어 double 타입의 유효 자릿수

C언어 double타입의 유효 자릿수는 보통 15~16자리이다.
위의 [풀이5]를 이해하면 왜 15~16자리라고 하는지 그 이유를 알아낼 수 있다.
배정밀도 부동 소수점으로 표현할 수 있는 수의 최댓값을 예시로 들어보면, 총 64비트로 된 부동 소수점은 최댓값일 때 아래와 같은 비트를 가지게 된다.
지수부 : 11111111110 (총 11비트) 가수부 : 1111111111111...(중략)...11 (총 52비트)
JavaScript
복사
이는 정규화된 수로 변환하면 다음과 같아진다. #[풀이5] 참고
(1+0.11111...)(2)∗21023(1 + 0.11111...)_{(2)} * 2^{1023}
이 값을 풀어보면 111111....1100000...0000(2)111111....1100000...0000_{(2)}이 되며 왼쪽부터 봤을 때, 11이 총 5353번 나온 다음, 00이 1023−52=9711023-52=971번 나온다.
이 중 유효한 숫자인 1만 모아보면 53자리의 수인 111111...11(2)111111...11_{(2)}이 되고 이는 10진법으로 변환하면 90071992547409919007199254740991이 된다. 즉, 16자리의 10진수이다.
때문에 double 타입의 유효 자릿수는 최대 “16자리”가 된다.

참고자료

Get the number 18437736874454810627
Thanks for contributing an answer to Stack Overflow! Please be sure to answer the question. Provide details and share your research! Asking for help, clarification, or responding to other answers. Making statements based on opinion; back them up with references or personal experience. To learn more, see our tips on writing great answers.
https://stackoverflow.com/questions/8105196/get-the-number-18437736874454810627
Double-precision floating-point format - Wikipedia
Double-precision floating-point format (sometimes called FP64 or float64) is a computer number format, usually occupying 64 bits in computer memory; it represents a wide dynamic range of numeric values by using a floating radix point.
https://en.wikipedia.org/wiki/Double-precision_floating-point_format
ECMAScript® 2021 Language Specification
https://262.ecma-international.org/12.0/
비정규 값 - 위키백과, 우리 모두의 백과사전
컴퓨터 과학에서 비정규 값(非正規값, denormal number) 또는 비정규화 값(非正規化값,denormalized number), 또는 준정규 값(準正規값, subnormal number)는 부동소수점 연산에서 0 주위의 언더플로 차이를 채워준다. 가장 작은 일반 숫자보다 더 작은 0이 아닌 값를 '비정규 값'이라고 한다. 일반적인 부동소수점 값에서는 가수 앞에 0이 한개 이상 선행할 수 없다. 이렇게 유효숫자의 첫자리를 1로 시작하도록 하는 과정을 정규화라고 한다.
https://ko.wikipedia.org/wiki/%EB%B9%84%EC%A0%95%EA%B7%9C_%EA%B0%92
Made with