14-1. 그래프의 이해와 종류
그래프의 역사와 이야깃거리
“모든 다리를 한 번씩만 건너서 처음 출발했던 장소로 돌아올 수 있는가?”
불가능하다. 정점 별로 연결된 간선의 수가 모두 짝수여야, 간선을 한 번씩만 지나서 처음 출발했던 정점으로 돌아올 수 있다
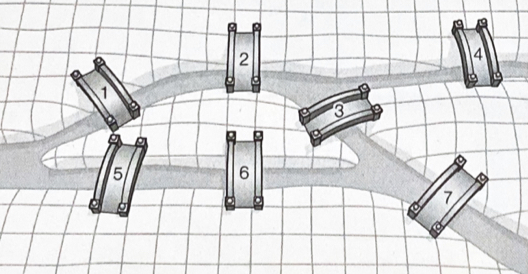
간선 : 다리정점 : 다리가 연결하는, 강으로 구분이 되는 땅
그래프의 이해와 종류
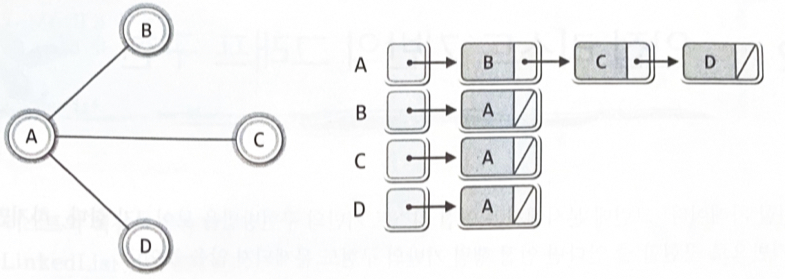
정점(vertex) : 연결의 대상이 되는 개체 또는 위치간선(edge) : 정점들 사이의 연결정점과 간선을 이용해 표현한 자료구조가 그래프
1.
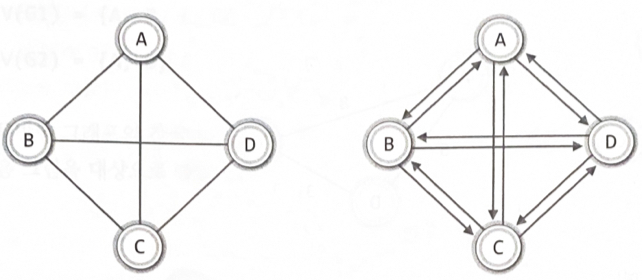
무방향 그래프(undirected graph): 연결 관계에 있어서 방향성이 없는 그래프
2.
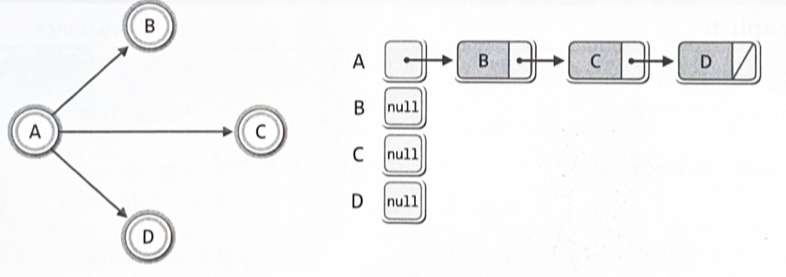
방향 그래프(directed graph) 혹은 다이그래프(digraph): 간선에 방향정보가 포함된 그래프
3.
완전 그래프: 각각의 정점에서 다른 모든 정점을 연결한 그래프방향 그래프의 정점의 수 = 무방향 그래프 정점의 수 x 2
가중치 그래프(Weigh Graph)와 부분 그래프(Sub Graph)
1.
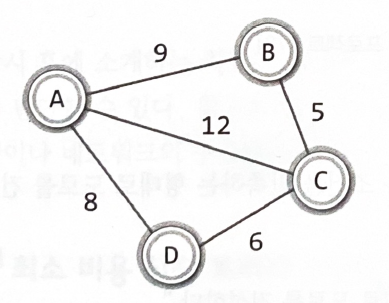
가중치 그래프: 간선에 가중치 정보를 두어서 구성한 그래프
2.
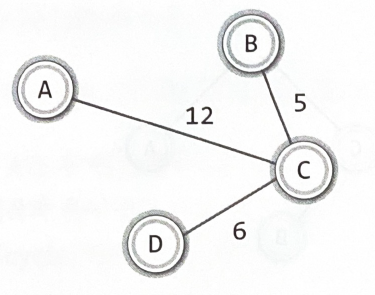
부분 그래프: 원 그래프의 일부 정점 및 간선으로 이뤄진 그래프
그래프의 집합 표현
1.
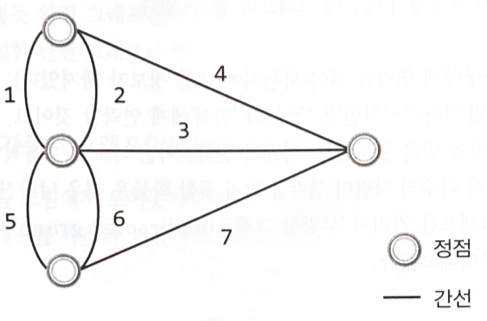
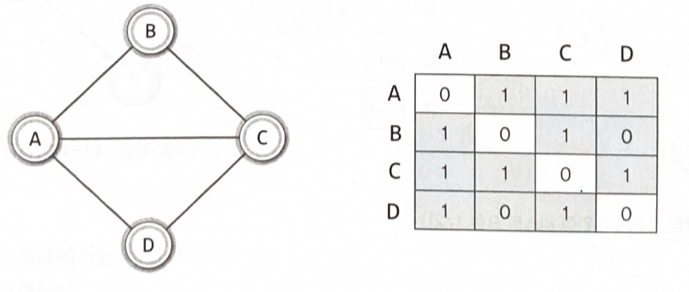
무방향 그래프
•
그래프 G의 정점 집합 : V(G)
•
그래프 G의 간선 집합 : E(G)
•
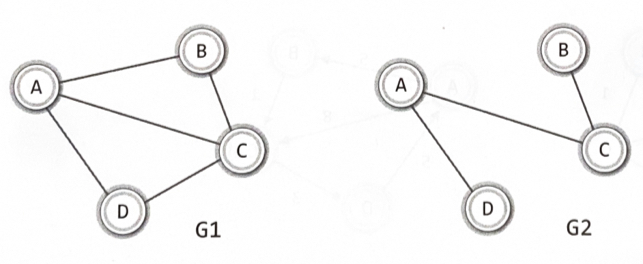
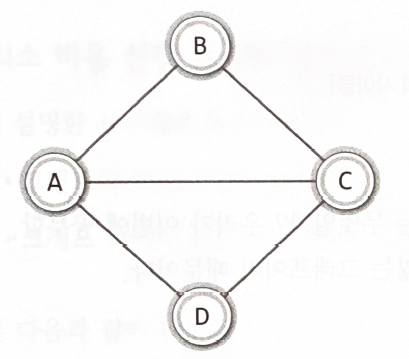
V(G1) = {A, B, C, D} E(G1) = {(A, B), (A, C), (A, D), (B, C), (C, D)}
•
V(G2) = {A, B, C, D} E(G2) = {(A, C), (A, D), (B, C)}
1.
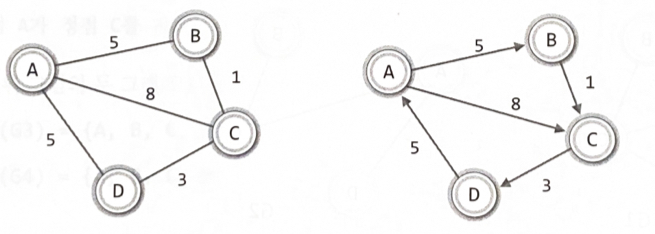
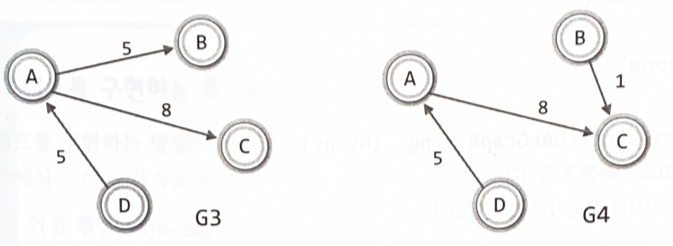
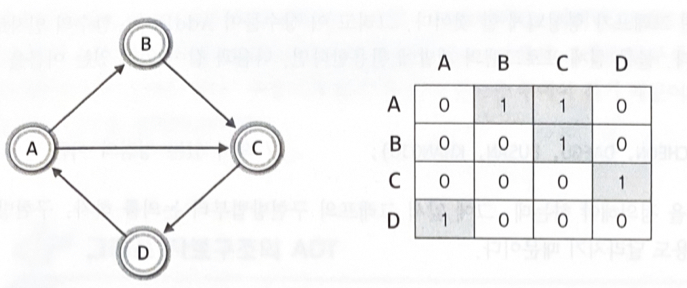
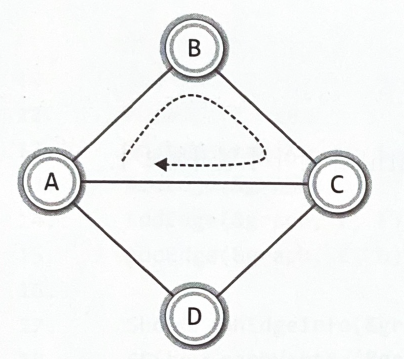
방향 그래프ex) 정점 A가 정점 C를 가리키는 간선 <A, C>
•
V(G3) = {A, B, C, D} E(G3) = {<A, B>, <A, C>, <D, A>}
•
V(G4) = {A, B, C, D} E(G4) = {<A, C>, <B, C>, <D, A>}
그래프의 ADT
그래프를 생성 및 초기화 할 때 간선의 방향성 여부를 선택할 수 있고, 가중치의 부여 여부도 선택할 수 있다. 뿐만 아니라, 이후에는 얼마든지 그리고 언제든지 정점과 간선을 삽입하고 삭제할 수 있다
void GraphInit(UALGraph * pg, int hv);
Plain Text
복사
•
그래프의 초기화를 진행한다.
•
두 번째 인자로 정점의 수를 전달한다.
void GraphDestroy(UALGraph *pg);
Plain Text
복사
•
그래프 초기화 과정에서 할당한 리소스를 반환한다.
void AddEdge(UALGraph * pg, int fromV, int toV);
Plain Text
복사
•
매개변수 fromV와 toV로 전달된 정점을 연결하는 간선을 그래프에 추가한다.
void ShowGraphEdgeInfo(UALGraph * pg);
Plain Text
복사
•
그래프의 간선정보를 출력한다
정점에 이름 부여enum {A, B, C, D, E, F, G, H, I, J}
•
정점 이름을 상수화ex) 함수의 두 번째 인자로 5가 전달되면 정점 A, B, C, D, E로 이뤄진 그래프 형성
그래프를 구현하는 두 가지 방법
1.
인접 행렬(adjacent matrix) 기반 그래프 : 정방 행렬을 활용1) 무방향 그래프
•
정점이 4개이면 가로 세로의 길이가 4인 2차원 배열 선언
•
두 정점이 연결되어 있으면 1로, 연결되어 있지 않으면 0으로 표시
•
간선에 방향성이 없기 때문에 하나의 간선에 대해서 두 개의 지점을 1로 표시2) 방향 그래프
•
무방향 그래프와 달리 대칭을 이루지 않는다
•
A에서 B로 향하는 간선의 표시를 위해서 [0][1]인 위치만 1로 표시
1.
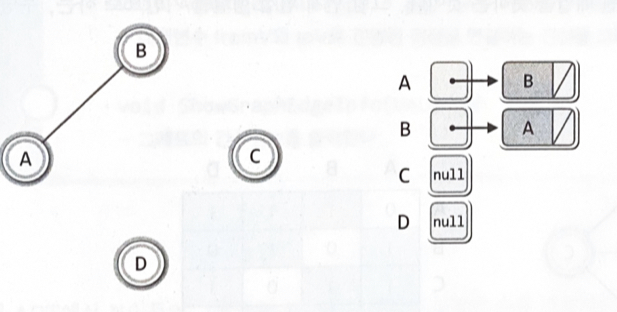
인접 리스트(adjacent list) 기반 그래프 : 연결 리스트를 활용1) 무방향 그래프
•
각각의 정점은 자신과 연결된 정점의 정보를 담기 위해서 하나의 연결 리스트를 갖는다
•
각각의 정점에 연결된 간선의 정보는 각각의 연결 리스트에 담아야 한다2) 방향 그래프
•
각 정점 별로 가리키는 정점의 정보만을 연결 리스트에 담는다
•
무방향 그래프에 비해서 추가되는 노드의 수가 반으로 준다
14-2. 그래프의 탐색
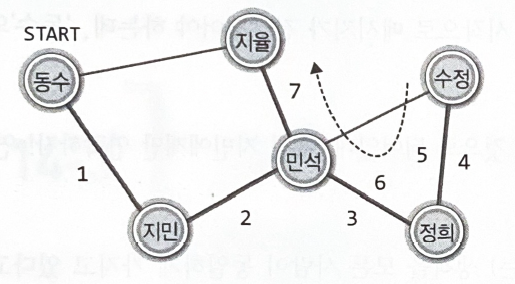
깊이 우선 탐색(Depth First Search : DFS)
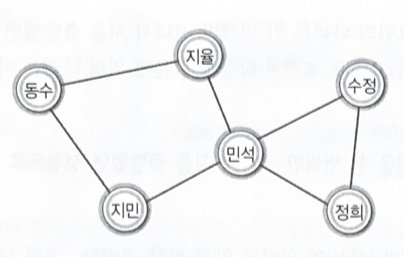
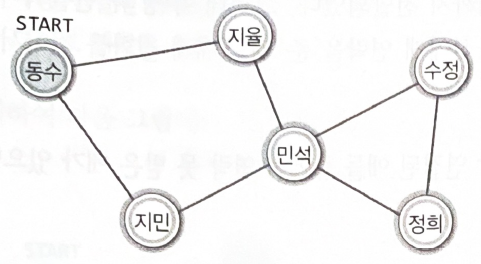
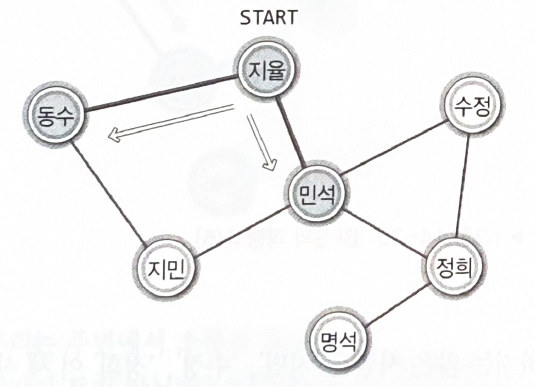
" 비상연락망을 보면 내가 지미과 지율에게 연락하는 것으로 되어있네. 우선 지미에게만 연락하자! 연락이 돌다 보면 지율에게도 연락이 갈 테니까"
한 사람에게만 연락한다는 생각
한 길을 깊이 파고드는 것
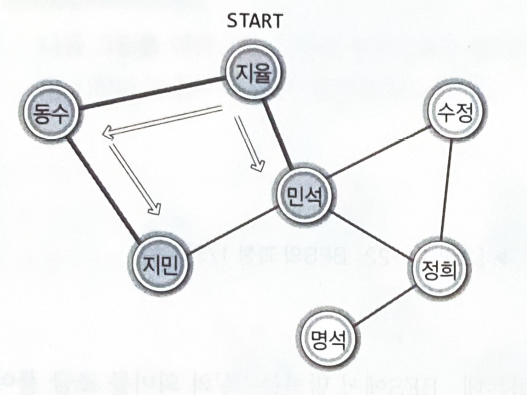
"나랑 연결된 애들은 다 연락을 받았어. 그러니까 너랑 연결된 애들 중에서 연락 못 받은 애가 있으면 그리로 연락을 줘!"
)
[DFS의 전체 과정]
한 사람에게만 연락을 한다.
•
연락할 사람이 없으면, 자신에게 연락한 사람에게 이를 알린다.
•
처음 연락을 시작한 사람의 위치에서 연락은 끝이 난다.
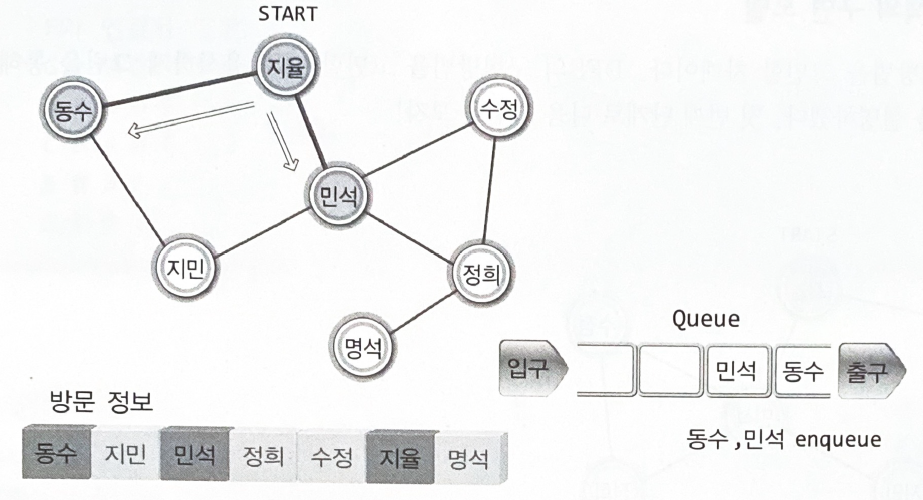
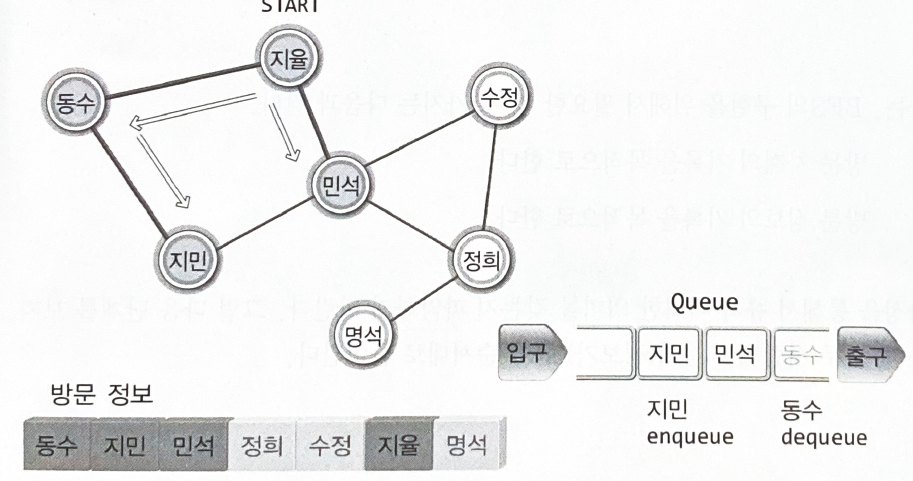
너비 우선 탐색(Breadth First Search : BFS)
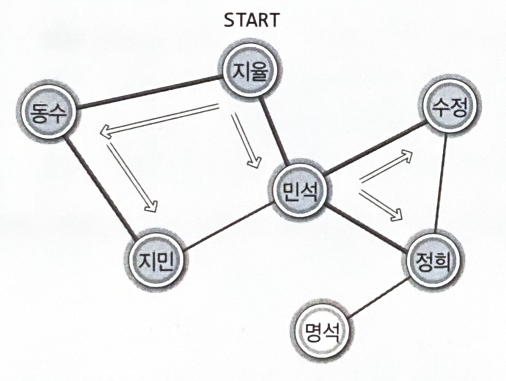
"한 사람을 기준으로 메시지를 전달하는 사람의 수(폭)"
"동수가 먼저 주변인에게 연락을 취하고, 이어서 민석이 주변인에게 연락을 취한다"
)
)
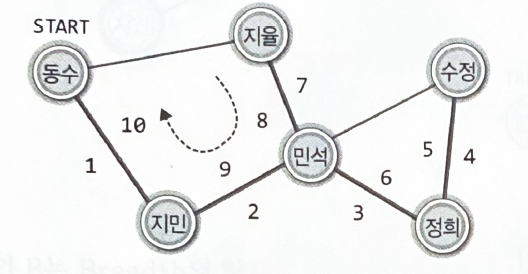
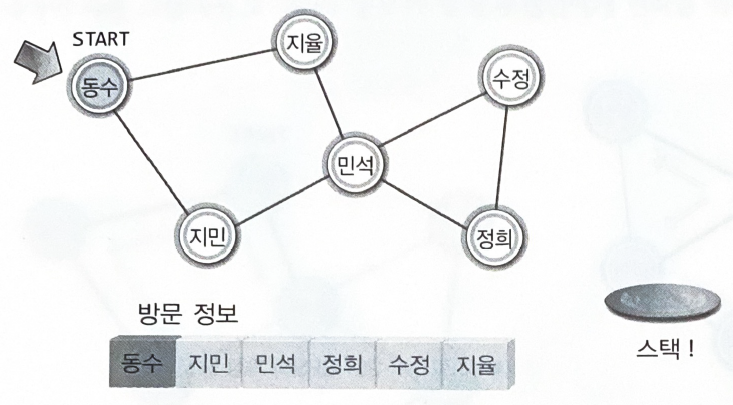
깊이 우선 탐색의 구현 모델
•
스택 : 경로 정보의 추적을 목적으로 한다
•
배열 : 방문 정보의 기록을 목적으로 한다
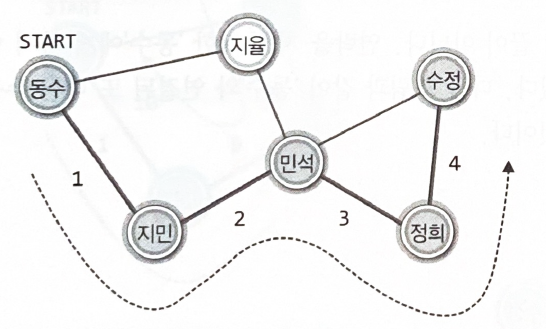
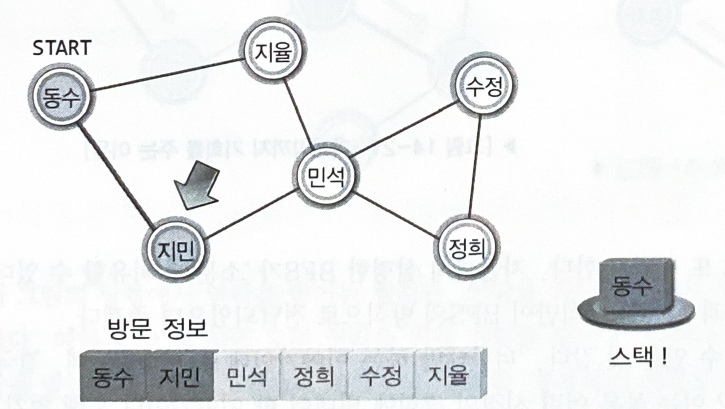
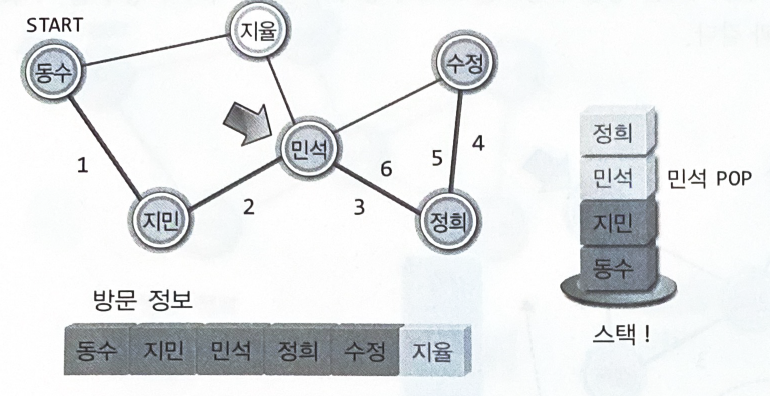
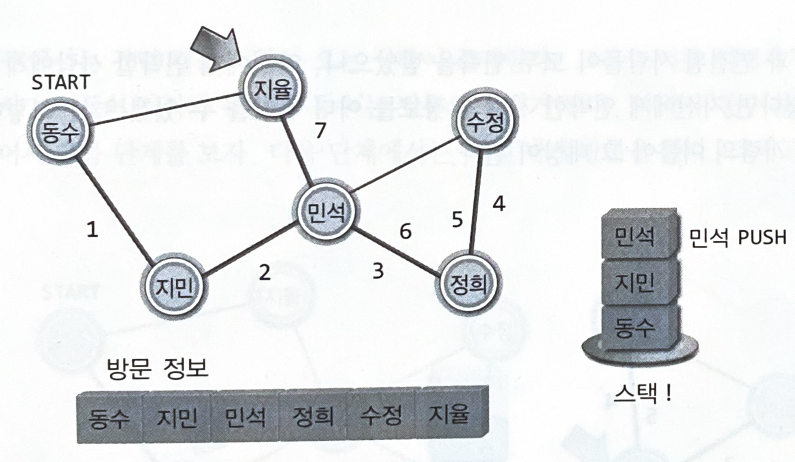
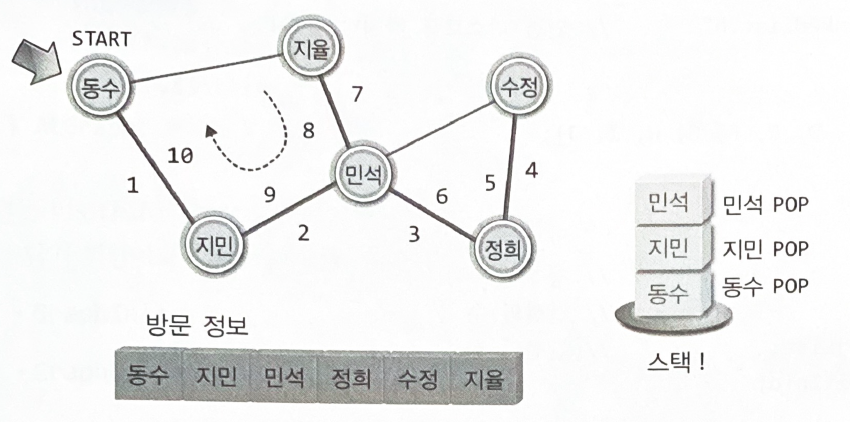
"동수를 떠나서 지민에게 방문할 때, 떠나는 동수의 이름(정보)을 스택으로 옮긴다"
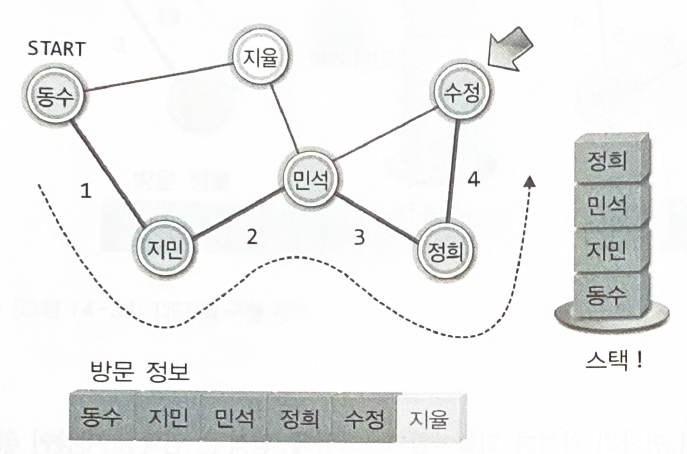
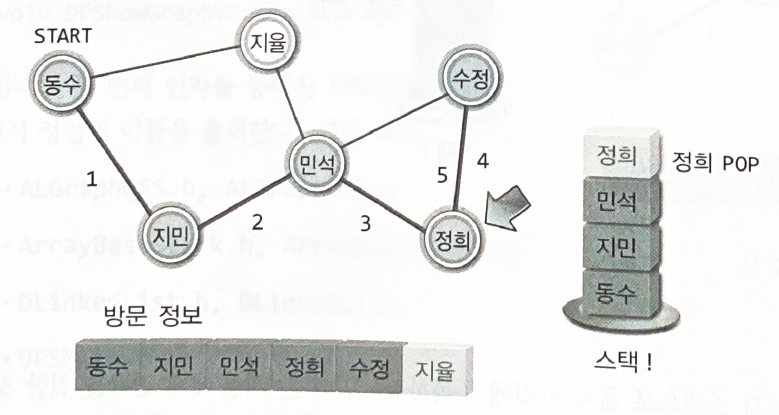
모두에게 연락을 돌리게 되면, 자신에게 연락한 사람의 정보를 스택에서 찾는다.
)
연락할 대상이 있는 사람을 찾으면 다시 스택으로 옮긴다.
)
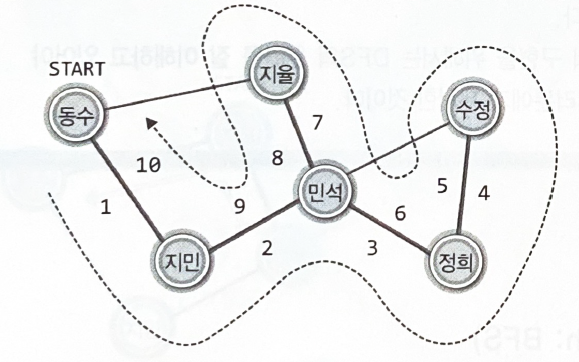
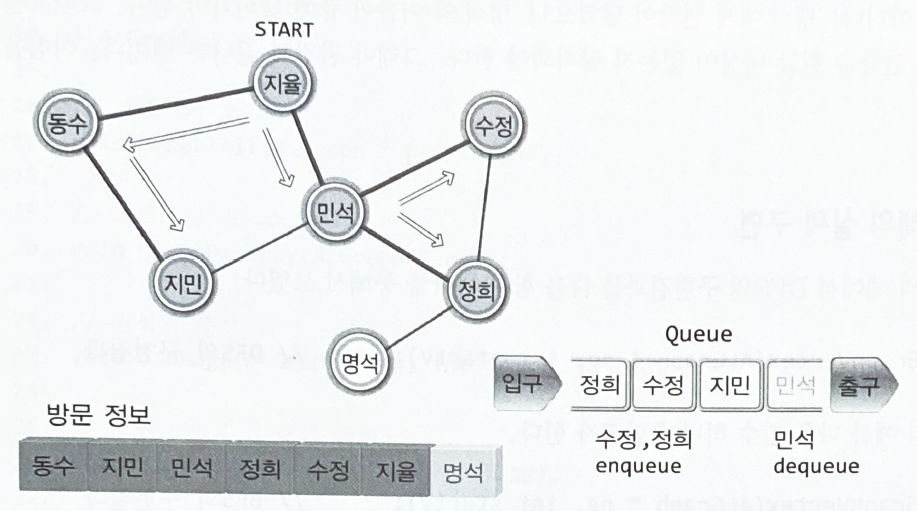
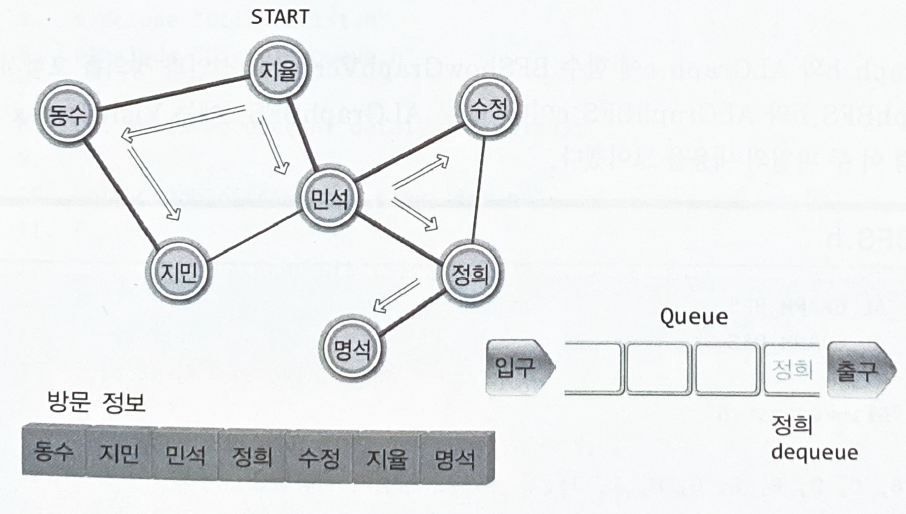
너비 우선 탐색의 구현 모델
•
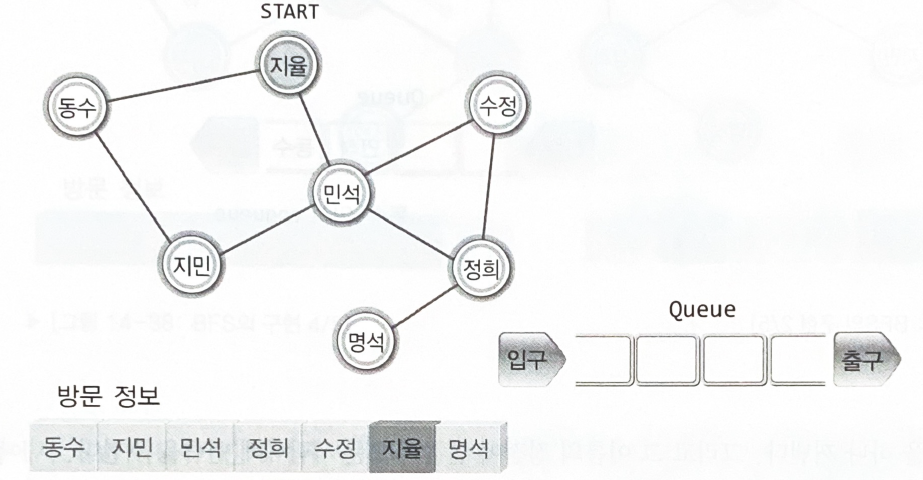
큐 : 방문 차례의 기록을 목적으로 한다.
•
배열 : 방문 정보의 기록을 목적으로 한다.
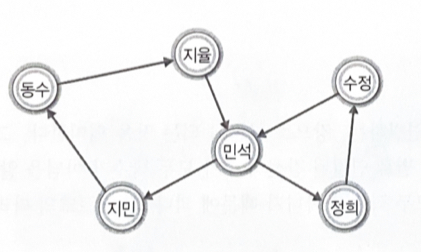
연락을 받은 두 사람의 이름이 큐에 들어가고, 큐에서 이름을 하나 꺼내어 그 이름의 정점에 연결된 모든 사람에게 연결을 취한다.
)
)
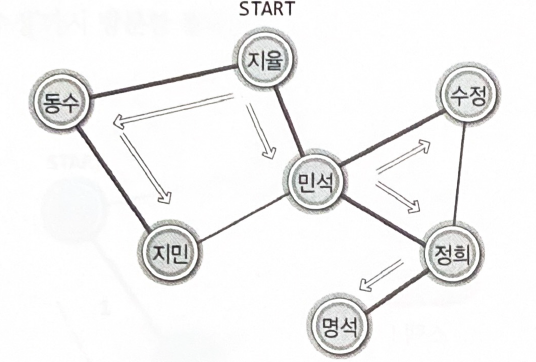
'명석'의 이름이 큐에 들어가고, '명석'을 꺼내어 '명석'이 연락을 취할 대상이 없는지까지 살펴봐야 한다.
14-3. 최소 비용 신장 트리
사이클(Cycle)을 형성하지 않는 그래프
정점 B에서 정점 D에 이르는 경로
•
B - A - D
•
B - C - D
•
B - A - C - D 조금 돌아가는 경로
•
B - C - A - D 조금 돌아가는 경로
단순 경로: 동일한 간선을 중복하여 포함하지 않는 경로
단순 경로가 아닌 예
•
B - A - C - B - A - D B와 A를 잇는 간선이 두 번 포함됨
사이클: 단순 경로이면서 시작과 끝이 같은 경로
신장 트리(spanning tree): 사이클을 형성하지 않는 그래프
최소 비용 신장 트리의 이해와 적용
신장 트리의 특징
•
그래프의 모든 정점이 간선에 의해서 하나로 연결되어 있다
•
그래프 내에서 사이클을 형성하지 않는다
간선에 방향성이 부여된 방향 그래프를 대상으로도 신장트리를 구성할 수 있다
최소 비용 신장 트리 or 최소 신장 트리: 간선의 가중치 합이 최소인 그래프
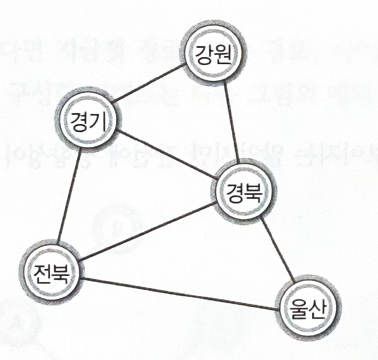
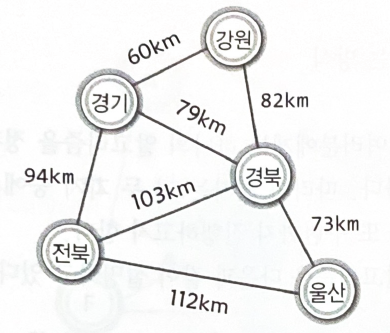
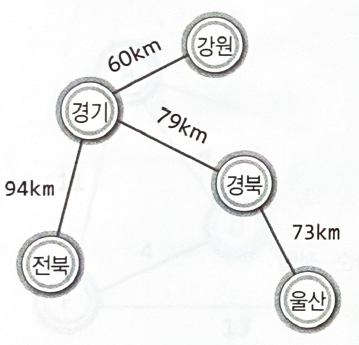
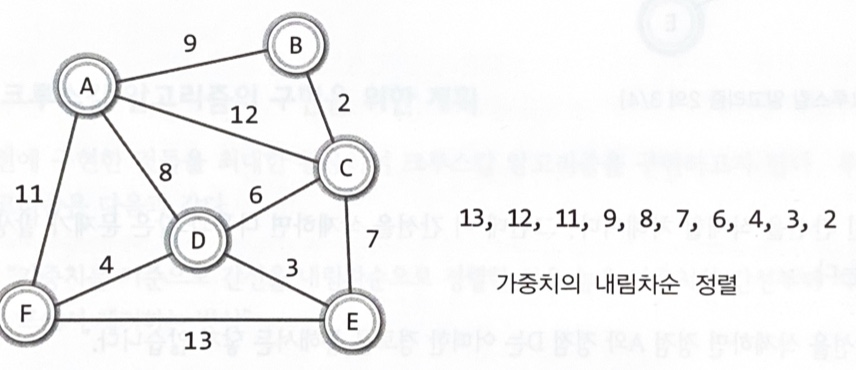
[도로 건설 프로젝트]강원, 경기, 경북, 울산, 전북을 직선으로 연결하는 물류에 특화된 도로를 건설하려고 한다.
"다섯 개의 지역이 모두 연결되게 하되, 그 거리를 최소화하는 형태로 도로를 건설한다"
)
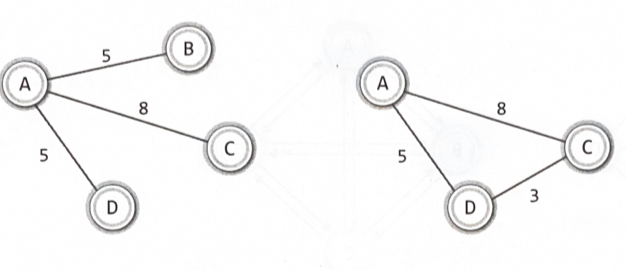
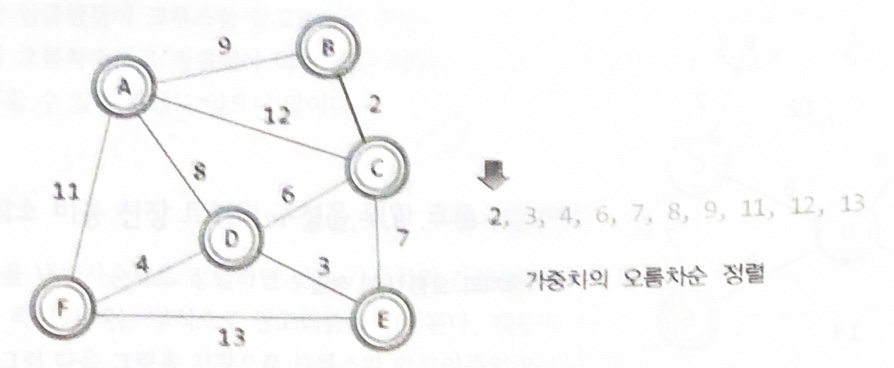
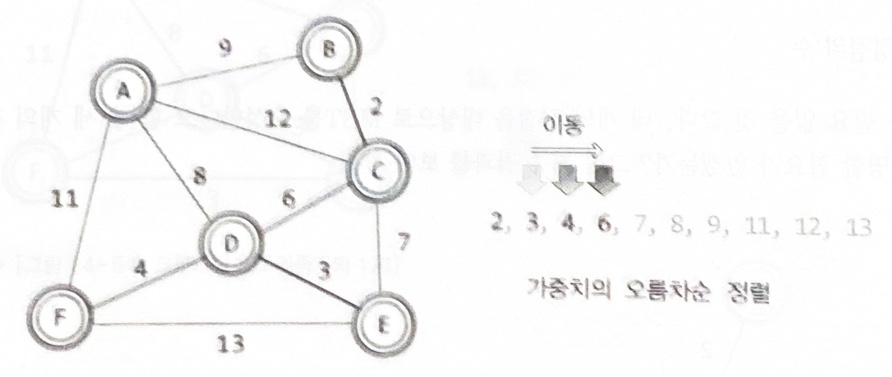
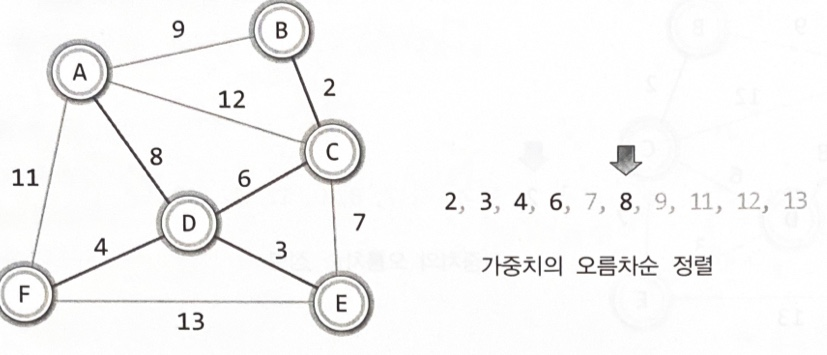
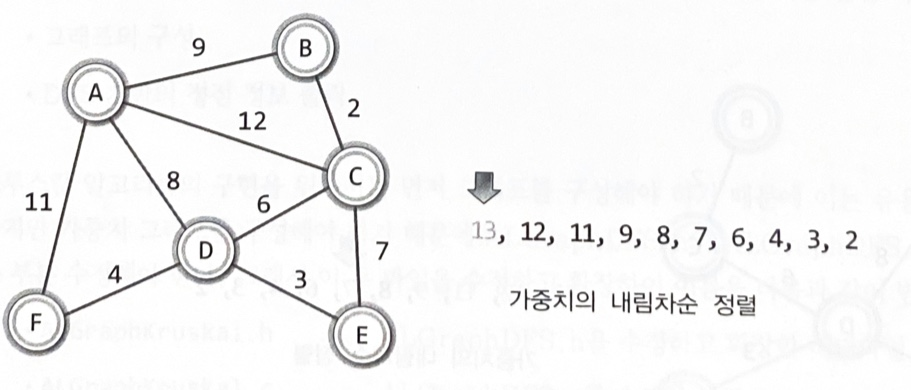
최소 비용 신장 트리의 구성을 위한 크루스칼 알고리즘1
•
크루스칼(Kruskal) 알고리즘: 가중치를 기준으로 간선을 정렬한 후, MST가 될 때까지 간선을 하나씩 선택하거나 삭제
•
프림(Prim) 알고리즘: 하나의 정점을 시작으로 MST가 될 때까지 트리를 확장
)
)
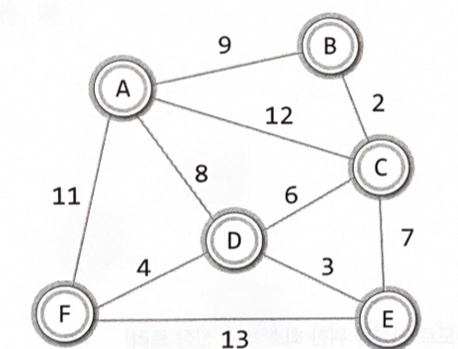
가중치가 7인 간선을 추가하면 그래프 내에 사이클이 형성된다
간선의 수 + 1 = 정점의 수
•
가중치를 기준으로 간선을 오름차순으로 정렬한다
•
낮은 가중치의 간선부터 시작해서 하나씩 그래프에 추가한다
•
사이클을 형성하는 간선은 추가하지 않는다
•
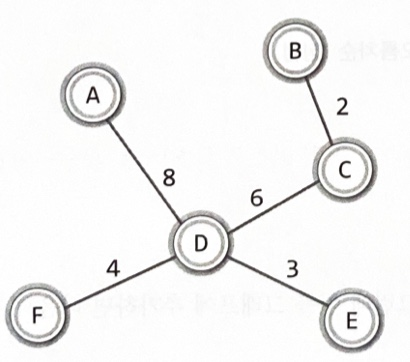
간서의 수가 정점의 수보다 하나 적을 때 MST가 완성된다
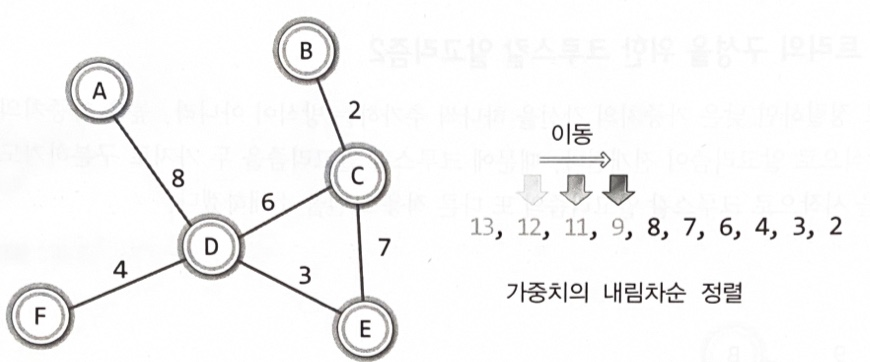
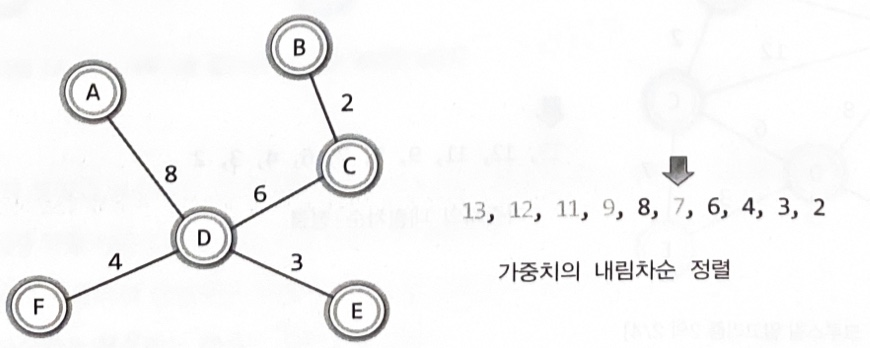
최소 비용 신장 트리의 구성을 위한 크루스칼 알고리즘2
)
)
가중치가 8인 간선을 삭제하게 되면 정점 A와 정점 D는 어떠한 경로를 통해서든 닿지 않는다
MST의 모든 정점은 간선에 의해서 하나로 연결되어야 한다
•
가중치를 기준으로 간선을 내림차순으로 정렬한다.
•
높은 가중치의 간선부터 시작해서 하나씩 그래프에서 제거한다.
•
두 정점을 연결하는 다른 경로가 없을 경우 해당 간선은 제거하지 않는다.
•
간선의 수가 정점의 수보다 하나 적을 때 MST는 완성된다.