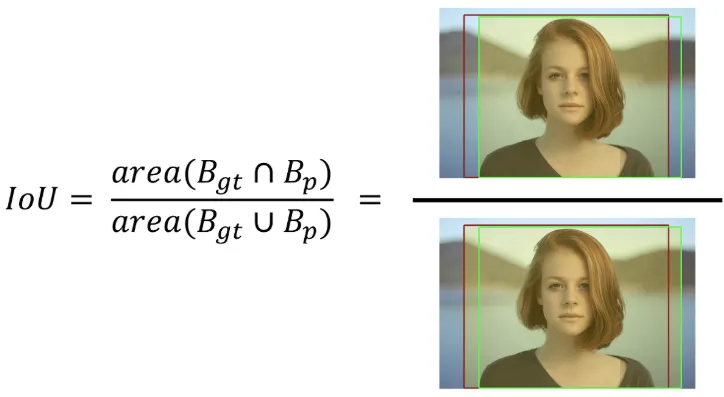머신러닝 분류 모델의 성능 평가 지표 분석
1. Precision and Recall
recall(재현율) : 실제 정답들 중에서 모델이 실제로 맞춘 비율
모델을 평가하는 요소는 결국, 모델이 내놓은 답과 실제 정답의 관계로서 정의를 내릴 수 있음. 정답이 True와 False로 나누어져있고, 분류 모델 또한 True False 의 답을 내놓기때문에, 아래와 같이 case를 나눌 수 있다.
•
True Positive (TP) : 실제 True인 정답을 True라고 예측 (정답)
•
False Positive (FP) : 실제 False인 정답을 True라고 예측 (오답)
•
False Negative (FN) : 실제 True인 정답을 False라고 예측 (오답)
•
True Negative (TN) : 실제 False인 정답을 False라고 예측 (정답)
1.1 Precision (정밀도)
정밀도란 모델이 True라고 분류한 것들 중에서 실제 True인 것들의 비율이다. 즉, 아래와 같은 식으로 표현 가능하다.
날씨 예측 모델이 맑다 로 예측했는데, 실제로 날씨가 맑았는지를 살펴보는 지표라고 할 수 있다.
1.2 Recall (재현율)
재현율이란 실제 True인 것들 중에서 모델이 True라고 예측한 것의 비율이다.
실제 날씨가 맑은 날들중, 모델이 날씨가 맑다고 맞춘 비율을 살펴보는 지표라고 할 수 있다.
1.3 Precision과 Recall
그럼 Precision(정밀도)과 Recall(재현율) 중 어떤 지표가 더 중요할까?
정답은 둘 다 중요하다 이다. 다음 예시를 살펴보자.
" 어떤 요소에 의해, 확실히 맑은 날을 예측할 수 있다면 해당하는 날에만 맑은 날이라고 예측하면 되겠다. "
이 경우에는 확실하지 않은 날에는 아예 예측을 하지 않고 보류하여 FP의 경우의 수를 줄일 수 있다.
그렇게 되면 Precision 은 높아지게 된다. 그러나 한달 30일 동안 맑은 날이 20일 이었는데 확실한 2일만 맑다고 예측을 한다면, 당연히 맑다고 한 날 중에 실제 맑은 날은 100%가 나오게 된다.
•
•
반대로 모든 날이 맑다. 라고 예측하는 모델이라면 TP 의 수를 끌어올려서 Recall 을 높일수가 있다. 한달 30일 동안 맑은 날이 20일 이었는데 30일 모두 맑다고 예측을 한다면, 당연히 맑았던 날 20일 중 실제 맑았다고 한 날은 100%가 나오게 된다.
•
•
위의 두 모델들은 각각 정밀도와 재현율이 100%이다. 그러나 이러한 모델이 이상적이진 않다. 그렇기때문에 모델을 검증하기 위해선 Precision과 Recall을 함께 고려해서 모델을 평가해야한다.
2. Accuracy (정확도)
이제는 관점을 좀 달리해서 생각해보자. 위의 두 지표는 모두 True를 True라고 옳게 예측한 경우에 대해서만 다루었다. 하지만, False를 False라고 예측한 경우도 옳은 경우이다. 이때, 해당 경우를 고려하는 지표가 바로 정확도 (Accuracy)이다. 식은 다음과 같다.
정확도는 가장 직관적으로 모델의 성능을 나타낼 수 있는 평가지표이다. 하지만, 여기서 고려해야하는 것이 있다. 바로 domain의 편중이다. 만약 우리가 예측하고자 하는 한달이 여름이기 때문에 눈오는 날이 흔치 않다고 생각해보자. 이 경우에는 해당 data의 domain이 불균형하게 되므로 맑은 것을 예측하는 성능은 높지만, 눈이 오는 것을 예측하는 성능은 매우 낮을 수 밖에 없다. 따라서 이를 보완할 지표가 필요하다.
3. F1 Score
3.1 F1 Score
F1 Score 는 Precision(정밀도) 와 Recall(재현율) 의 조화평균 입니다.
F1 Score는 데이터 label이 불균형 구조일 때, 모델의 성능을 정확하게 평가할 수 있으며, 성능을 하나의 숫자로 표현할 수 있다. 여기서 단순 산술 평균으로 사용하지 않는 이유는 무엇일까? 평균 속력을 구할 때, 이 조화평균의 개념을 사용해 본 경험이 있을 것이다. 조화평균의 본질에 대해 이해해 보겠다.
3.2 조화평균의 기하학적 접근
서로 다른 길이의 A, B와 이 두 길이의 합만큼 떨어진 변(AB)로 이루어진 사다리꼴을 생각해보자. 이 AB에서 각 변의 길이가 만나는 지점으로부터 맞은 편의 사다리골의 변으로 내린 선분이 바로 조화평균을 나타낸다.
기하학적으로 봤을 때, 단순 평균이라기 보다는 작은 길이 쪽으로 치우치게 된, 그러면서 작은 쪽과 큰 쪽의 사이의 값을 가진 평균이 도출된다. 이렇게 조화평균을 이용하면 산술평균을 이용하는 것보다, 큰 비중이 끼치는 영향이 줄어든다고 볼 수 있다.
<F1 Score 의 기하학적 의미>
4. mAP
합성곱 신경망 (Convolutional Neural Network CNN) 의 모델 성능 평가는 대체로 mAP를 이용하여 평가한다. mAP 를 이해하기 위해서는 먼저 IoU와 AP에 대해 이해해야 한다.
4.1 IoU (Intersect over Union)
객체탐지 모델에서 "물체를 옳게 검출했다." , "물체가 옳게 검출되지 않았다." 를 구분하는 기준이 바로 IoU 이다.
사용자가 인물의 위치에 적용한 바운더리 박스와, 바운더리 박스가 주어지지 않은 상황에서 어떤 모델이 예측한 바운더리 박스라고 가정해보자.
이때 모델이 설정한 바운더리 박스가 맞는지 틀린 지를 결정하기 위해서 나온 것이 IoU 이다. IoU 는 아래의 그림과 같이 구해진다. 예측된 바운더리 박스와 사용자가 설정한 바운더리 박스 간 중첩되는 부분의 면적을 측정해서 중첩된 면적을 합집합의 면적으로 나눠준다.
보통의 경우 IoU의 계산 결과 값이 0.5 이상이면 제대로 검출(TP)되었다고 판단한다. 만약 0.5 미만이면 잘못 검출(FP) 되었다고 판단한다. (이 값은 임의의 값으로 설정할 수 있다.)
4.2 Precision-recall 곡선
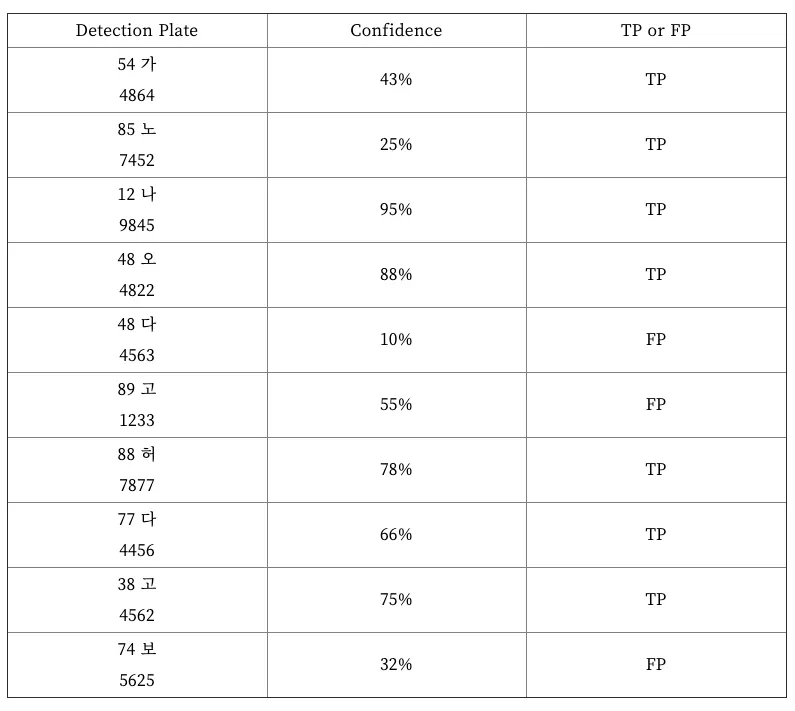
Precision-recall 곡선 (PR곡선)은 물체를 검출하는 알고리즘의 성능을 평가하는 방법 중 하나로 confidence레벨에 대한 threshold 값의 변화에 따라 precision과 recall 값들도 달라진다. confidence는 검출한 것에 대해 모델이 얼마나 정확하다고 생각하는지 알려주는 값이다. 만약 어떤 물체를 검출했을 때 confidence 레벨이 0.99 라면 모델은 그 물체가 검출해야 하는 물체와 거의 똑같다고 생각하는 것과 같다. 하지만 confidence 레벨이 높다고 해서 무조건 정확한 것이 아니다. 모델이 그저 학습한 것에 따른 정확도를 나타내는 것이다. 사용자는 보통 confidence 레벨에 대해 threshold 값을 부여해서 특정값 이상이 되어야 검출된 것으로 인정한다. threshold 값이 0.4 라면 confidence 레벨이 0.4 미만인 검출은 무시하는 것이다. 따라서 이 threshold 값의 변화에 따라 precision과 recall 값들도 달라질 것이다. 이것을 그래프로 나타낸 것이 바로 PR 곡선이다. 15개의 번호판이 존재하는 이미지에서 총 10개의 이미지가 검출되었다고 가정해보자.
10개 중 7개가 제대로 검출되었고, 3개는 잘못 검출되었다. 이때 Precision과 Recall 값은 아래와 같다.
이것은 confidence 레벨이 10%와 같이 아주 낮더라도 검출해낸 것들을 모두 인정했을 때의 결과이다.
검출된 결과를 confidence 레벨에 따라 오름차순으로 재정렬 해보자. confidence 레벨에 대한 threshold 값을 아주 엄격하게 적용해서 90%로 했다면, 하나만 검출한 것으로 판단할 것이고, 이때 Precision = 1/1 = 1, Recall = 1/15 = 0.067 이 된다. threshold 값을 85%로 했다면, 두개가 검출된 것으로 판단할 것이고, 이때 Precision = 2/2 = 1, Recall = 2/15 = 0.13 이 된다. 이렇게 threshold 값을 confidence 레벨에 맞춰 낮춰가면 다음과 같이 precision과 recall 이 계산될 것이다.
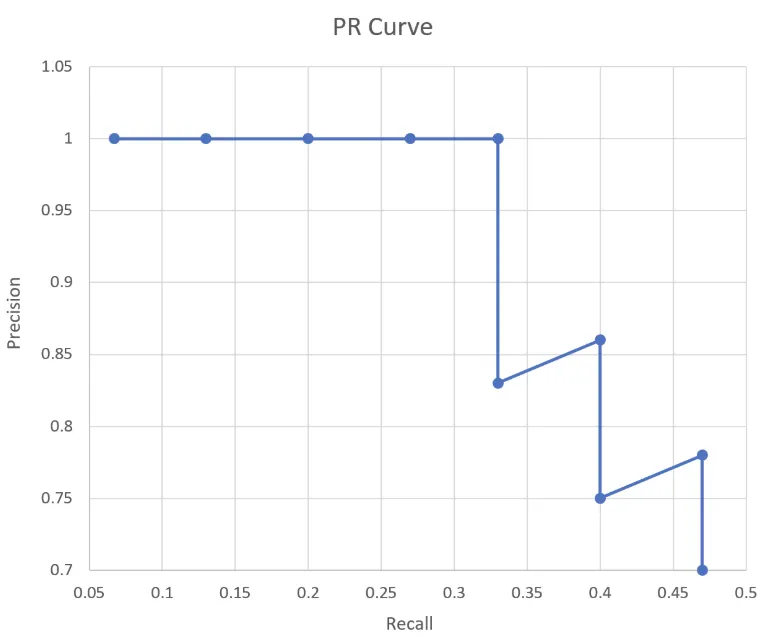
이 Precision 값들과 Recall 값들을 아래와 같이 그래프로 나타내면 그것이 바로 PR 곡선이다. PR 곡선에서 x축은 Recall 값이고, y축은 Precision 값이다. 즉, PR 곡선에서는 Recall 값의 변화에 따른 Precision 값을 확인할 수 있다.
4.3 AP (Average Precision) 와 mAP
PR 그래프는 어떤 모델의 성능을 전반적으로 파악하기에는 좋으나 서로 다른 두 모델의 성능을 정량적으로 비교하기에는 불편한 점이 있다. 그래서 나온 개념이 Average Precision 이다. AP는 인식 알고리즘의 성능을 하나의 값으로 표현한 것으로서 PR 그래프에서 그래프 선 아래쪽의 면적으로 계산된다. AP 가 높으면 높을수록 그 모델의 성능이 전체적으로 우수하다는 의미이다. 컴퓨터 비전 분야에서 물체인식 알고리즘의 성능은 대부분 AP로 평가한다.
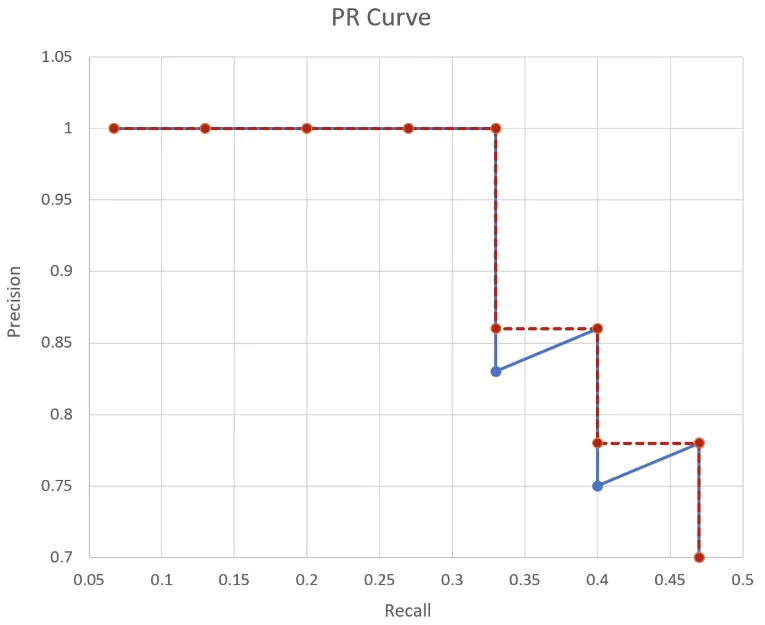
보통 계산 전에 PR 곡선을 단조적으로 감소하는 그래프로 변경해준다. 이렇게 바꾼 다음에 그래프 선 아래의 넓이를 계산함으로서 AP를 구한다. 이 경우 AP는 1 * 0.33 + 0.86 * 0.07 + 0.77 * 0.06 = 0.4364 가 된다.
컴퓨터 비전 분야에서 물체 검출 및 이미지 분류 모델의 성능은 대부분 이 AP로 평가한다. 물체 클래스가 여러 개인 경우 각 클래스당 AP를 구한 다음에 그것을 모두 합한 후 물체 클래스의 갯수로 나눠줌으로서 모델의 성능을 평가한다. 이것을 mAP (mean Average Precision) 이라고 한다.