포토샵은 곡선을 어떻게 그릴까?
대부분 이 Pen tool을 이용해서 작품을 만들어냅니다.
이 글에선 디자이너들의 필수 템, 어도비 포토샵-일러스트레이터의 Pen tool 원리에 대해
간략히 소개하고자 한다.
어도비 펜 툴은 디자이너가 곡선을 편집할 수 있도록 4개의 Control Point를 제공한다.
이러한 Contol point based curve는 프랑스 르노자동차의 엔지니어였던 Pierre Bezier가 제안하여
Bezier Curve라고 불린다.
Bézier Curve
베지어 커브를 이용하면 직선과 곡선 모두 그릴 수 있다.
커브 그리기에 사용된 점이 2개일 때는 직선이고, 점이 3개 이상일 때부터 곡선이 된다.
점 2개부터 점 4개까지 순서대로 설명하겠다.
점 2개 연결하기 (no control point, 직선)
•
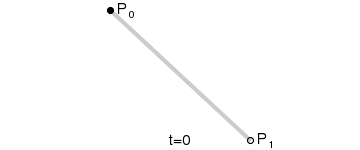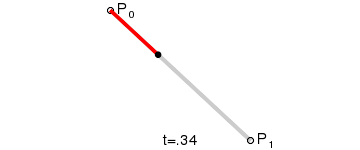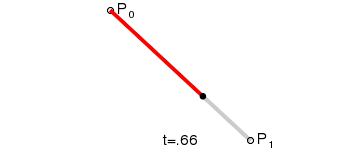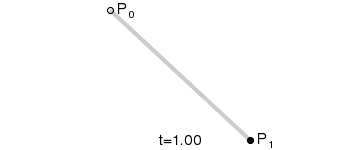
2개의 점 P0, P1가 있을 때 [P0 → P1] Vector 는 (두 점의 차) 이다.
따라서 P0과 P1를 잇는 선은 (0≤t≤1) 로 표현 가능하다.
(t는 0부터 1까지 점점 증가)
이는 식을 풀면 (0≤t≤1) 로 표현할 수 있다.
이때 t=0이면 점 P0이고, t=0.5이면 P0과 P1의 중간지점이며, t=1이면 점 P1이다.
점 3개 연결하기 (1 control point, 곡선)
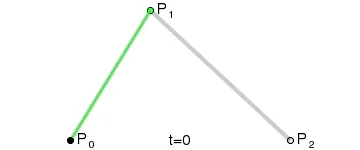
번, 점2개 잇기를 응용하면 점 3개를 이용한 식을 도출 할 수 있다.제시된 점 3개 P0,P1,P2를 이용해서, 위 그림의 움직이는 검은 점(K3라고 하겠음)을 구하면 된다.
1.
두점 P0 ~ P1 사이를 움직이는 점 K1(위 그림의 왼쪽 녹색 점)
K1 = (0≤t≤1)
2.
두점 P1 ~ P2 사이를 움직이는 점 K2(위 그림의 오른쪽 녹색 점)
K2 = (0≤t≤1)
3.
위에서 도출한 두 점 K1 과 K2 사이를 움직이는 점 K3(그림의 중간 검은 점)
K3 = (0≤t≤1)
4.
K1 과 K2를 위 (1)번식과 (2)번식을 대입하면 아래와 같다.
K3 = (0≤t≤1)
5.
이를 풀어서 정리하면…
이 때 t=0이면 P1이 나오고, t=1 이면 P3가 나온다.
점 4개 연결하기 (2 control point, 곡선)
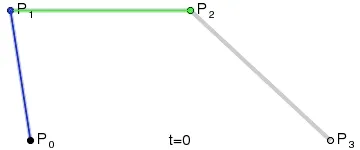
번, 점3개 잇기의 과정을 점 4개에 대해 동일하게 적용하면 된다.위 그림의 검은 점 K4를 구하면 아래와 같은 식을 도출할 수 있다.
위 식을 4x4 Matrix(=상수)로 빼면 아래와 같은 행렬로 정리할 수 있다.
( 아래 그림은 t가 u로 바뀜 )
아래 그림은 t가 u로 바뀜 ) 
재귀 호출을 통한 코드 구현
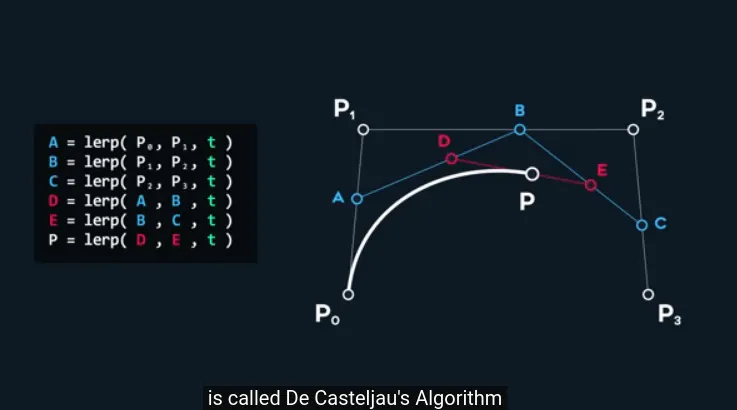
위 과정을 보면, 점의 위치 도출 과정이 재귀적이다.
따라서 위에서 구한 식을 모르더라도
번, 점2개 잇기를 재귀함수를 통해 점 4개에 대한 식을 쉽게 구현 수 있으며
이렇게 재귀적으로 구하는 베지어 곡선을 De Casteliau’s Algorithm 이라고 부른다.
번, 점2개 잇기를 재귀함수를 통해 점 4개에 대한 식을 쉽게 구현 수 있으며
이렇게 재귀적으로 구하는 베지어 곡선을 De Casteliau’s Algorithm 이라고 부른다.Recursive Step for P
… (이하 생략)
참고 자료
The Beauty of Bézier Curves
Bézier curves - how do they do?They're used for animation, text rendering, and all sorts of curved shapes! But how do they actually work? well, like, that's ...
https://youtu.be/aVwxzDHniEw
베지어 커브에 대한 보다 자세한 설명은 위 유투브 영상을 참조 바랍니다.
