목차
1. 우선순위 큐 ADT
(1) 소개
큐(Queue)는 먼저 들어오는 데이터가 먼저 나가는 FIFO(First In First Out) 형식의 자료 구조이다.
우선순위 큐(Priority Queue)는 우선순위가 높은 데이터가 먼저 나가는 형태의 자료 구조이다.
(2) 우선순위 큐의 연산
주요 연산
•
Insert(key, data)
◦
key에 따른 데이터를 우선순위 큐에 삽입한다.
◦
항목들은 key에 따라 정렬된다.
•
DeleteMin / DeleteMax
◦
DeleteMin: 가장 작은 key를 가진 항목을 삭제하고 리턴한다.
◦
DeleteMax: 가장 큰 key를 가진 항목을 삭제하고 리턴한다.
•
GetMininum / GetMaximum
◦
가장 작은/큰 키를 가진 항목을 삭제하지 않고 리턴한다.
보조 연산
•
kth-Smallest/kth-Largest
◦
우선순위 큐에서 k번째로 작거나/큰 키를 리턴한다.
•
size
◦
우선순위 큐 안의 항목의 개수를 리턴한다.
•
Heap Sort
◦
우선순위 큐의 항목을 우선순위(키)에 따라 정렬한다.
(3) 적용 사례
•
데이터 압축: 허프만(Huffman) 코딩 알고리즘
•
최단 거리 알고리즘: 다익스트라(Dijkstra)의 알고리즘
•
최소 신장 트리 알고리즘: 프림(Prim)의 알고리즘
•
이벤트 지향 시뮬레이션: 줄 서 있는 고객들
•
선택 문제: k번째 작은 항목 찾기
•
운영체제에서의 작업 스케줄링
(4) 구현 방법
구현 | 삽입 | 삭제(DeleteMin) | Find Min |
정렬되지 않은 배열 | 1 | n | n |
정렬되지 않은 리스트 | 1 | n | n |
정렬된 배열 | n | 1 | 1 |
정렬된 리스트 | n | 1 | 1 |
이진 검색 트리 | logn(평균) | logn(평균) | logn(평균) |
균형 이진 검색 트리 | logn | logn | logn |
이진 힙 | logn | logn | 1 |
정렬되지 않은 배열 구현
정렬되지 않은 리스트 구현
정렬된 배열 구현
정렬된 리스트 구현
이진 검색 트리 구현
균형 이진 검색 트리 구현
이진 힙 구현
2. 힙
(1) 힙이란?
•
힙(Heap)은 노드의 값이 그 자식 노드의 값보다 항상 크거나 같은 트리 구조를 말한다.(혹은 작거나 같다.) 이를 힙 속성(heap property)라고 한다.
•
힙은 완전 이진 트리의 일종이다. 즉, 트리의 높이를 h(h>0)라 할 때, 모든 잎 노드들은 h 또는 h-1 레벨에 있어야 한다.
•
여러 개의 값들 중에서 최댓값이나 최솟값을 빠르게 찾아내도록 만들어진 자료구조이다.
•
중복된 값은 허용한다.
(이진 탐색 트리에서는 중복 값을 허용하지 않는다.)
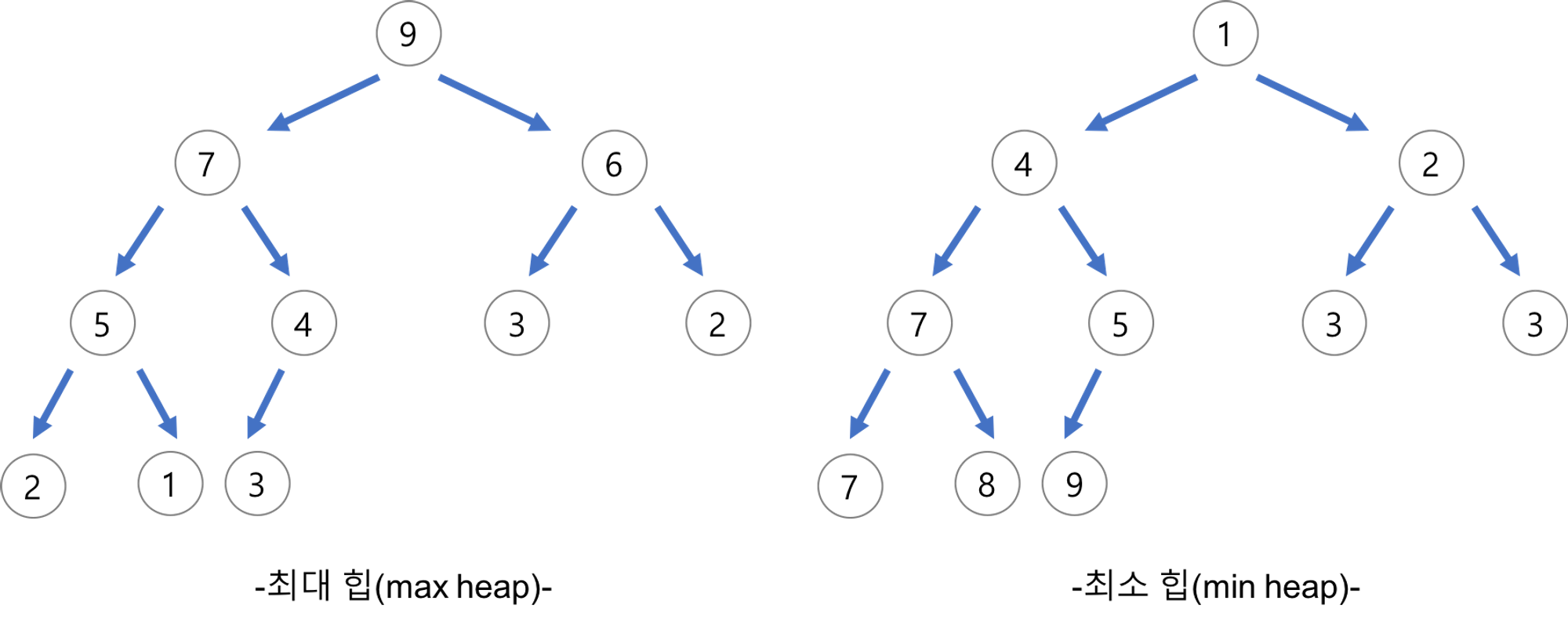
(2) 힙의 종류
•
최소 힙(Min Heap)
◦
노드의 값이 자식 노드의 값보다 작거나 같다.
•
최대 힙(Max Heap)
◦
노드의 값이 자식 노드의 값보다 크거나 같다.
3. 힙의 구현(with 배열)
(1) 힙의 선언
// 이진 힙의 선언
typedef struct _heap {
int* array;
int count; // 힙 안의 항목 개수
int capacity; // 힙의 용량
int heap_type; // 최소 힙인지 최대 힙인지
}Heap;
C
복사
(2) 힙의 생성
// 힙의 생성
Heap* CreateHeap(int capacity, int heap_type)
{
Heap* h = (Heap*)malloc(sizeof(Heap));
if (!h) {
printf("Memory Error"); //널 가드
return NULL;
}
h->heap_type = heap_type;
h->count = 0;
h->capacity = capacity;
h->array = (int*)malloc(sizeof(int) * h->capacity);
if (!h->array) {
printf("Memory Error\n"); //널 가드
return NULL;
}
return h;
}
C
복사
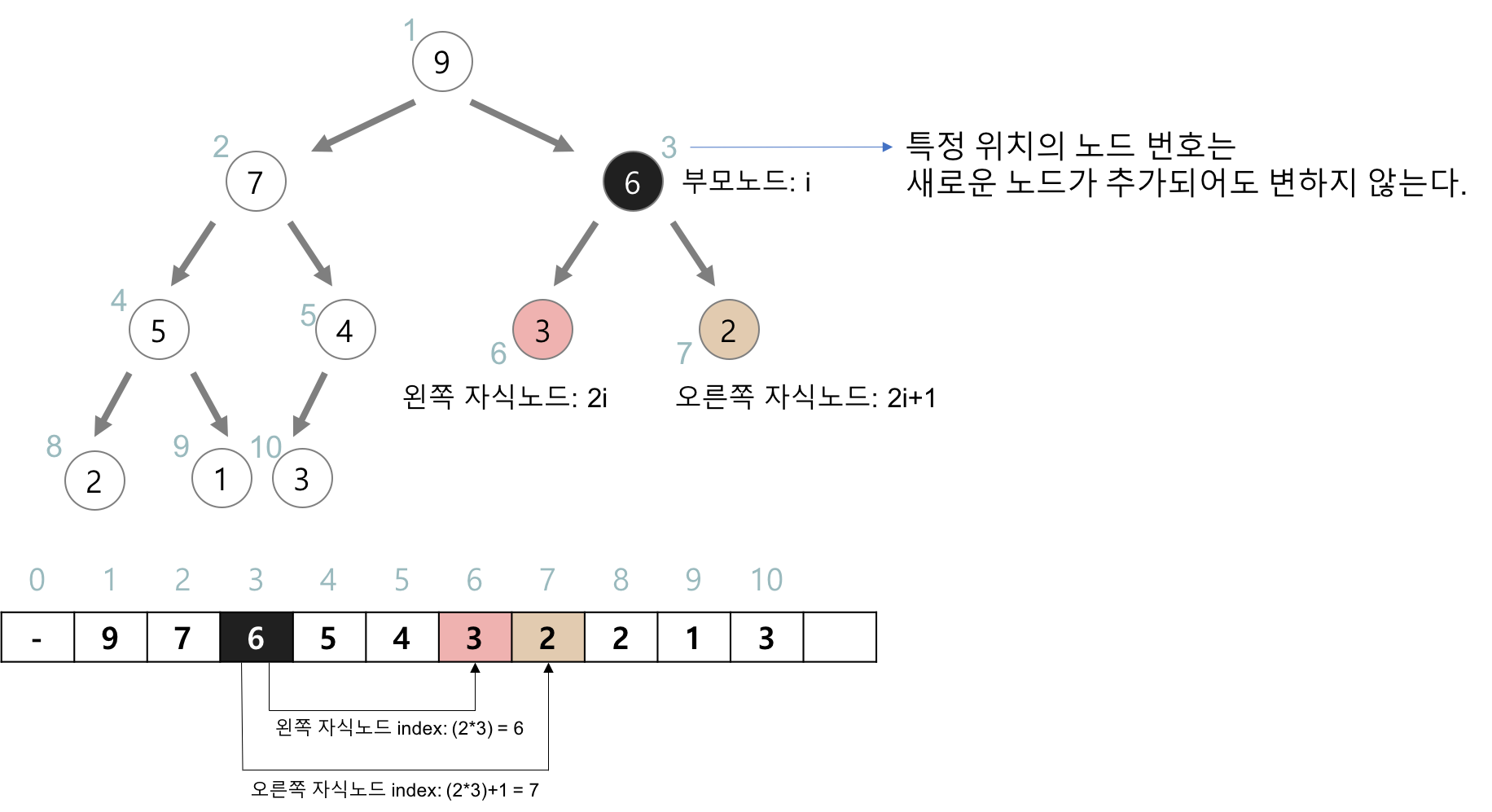
(3) 노드의 부모 노드 인덱스 찾기
// 노드의 부모 인덱스
int Parent(Heap* h, int i) {
if (i <= 0 || i >= h -> count)
return (-1);
return ((i - 1) / 2);
}
C
복사
(4) 노드의 자식 노드 인덱스 찾기
// 노드의 자식들
int LeftChild(Heap* h, int i) { // 왼쪽 노드
int left = 2 * i + 1;
if (left >= h->count) return -1;
return left;
}
int RightChild(Heap* h, int i) { // 오른쪽 노드
int right = 2 * i + 2;
if (right >= h->count) return -1;
return right;
}
C
복사
(5) 최대 항목 구하기 ( 최대 힙인 경우)
// 최대 항목 구하기(최대힙인 경우)
int GetMaximum(Heap* h) {
if (h->count == 0)
return -1;
return h->array[0];
}
C
복사
(6) 항목을 힙으로 만들기
// i 위치의 항목 힙으로 만들기
void PercolateDown(Heap* h, int i)
{
int l, r, max = i, tem;
l = LeftChild(h, i);
r = RightChild(h, i);
if (l != -1 && h->array[l] > h->array[max])
max = l;
if (r != -1 && h->array[r] > h->array[max])
max = r;
if (max != i)
{
// h->array[i] 와 h->array[max] 바꿔치기
tem = h->array[i];
h->array[i] = h->array[max];
h->array[max] = tem;
PercolateDown(h, max);
}
}
C
복사
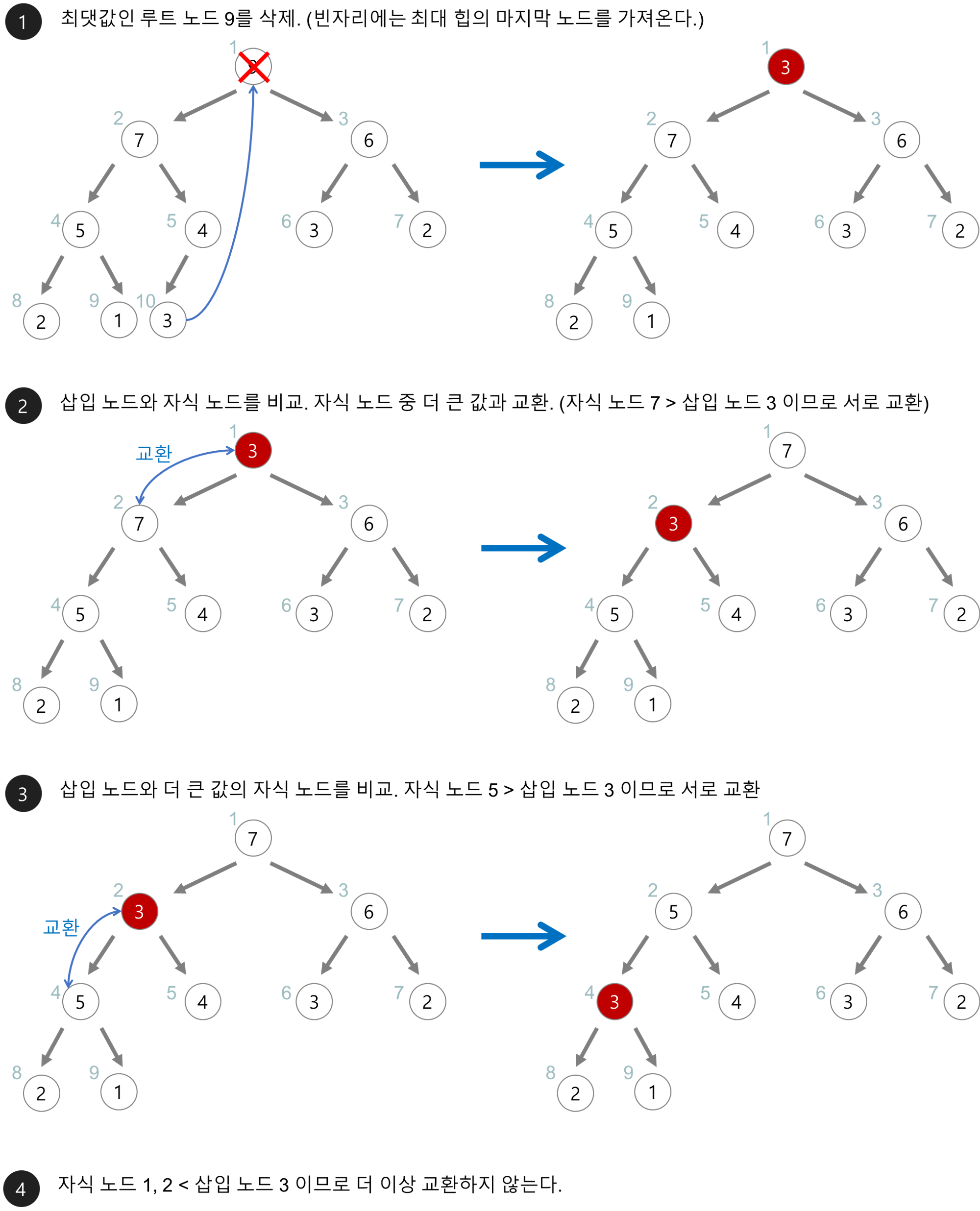
(7) 항목 삭제하기
// (뿌리) 항목 삭제하기
int DeleteMax(Heap* h)
{
int data;
if (h->count == 0)
return -1;
data = h->array[0]; // 첫번째 항목을 어떤 변수에 복사한다.
h->array[0] = h->array[h->count - 1]; // 마지막 항목을 첫 번째 항목의 위치에 복사한다.
h->count--; // 힙의 크기를 줄인다.
PercolateDown(h, 0); //첫 번째 항목에서 PercolateDown을 호출한다.
return data;
}
C
복사
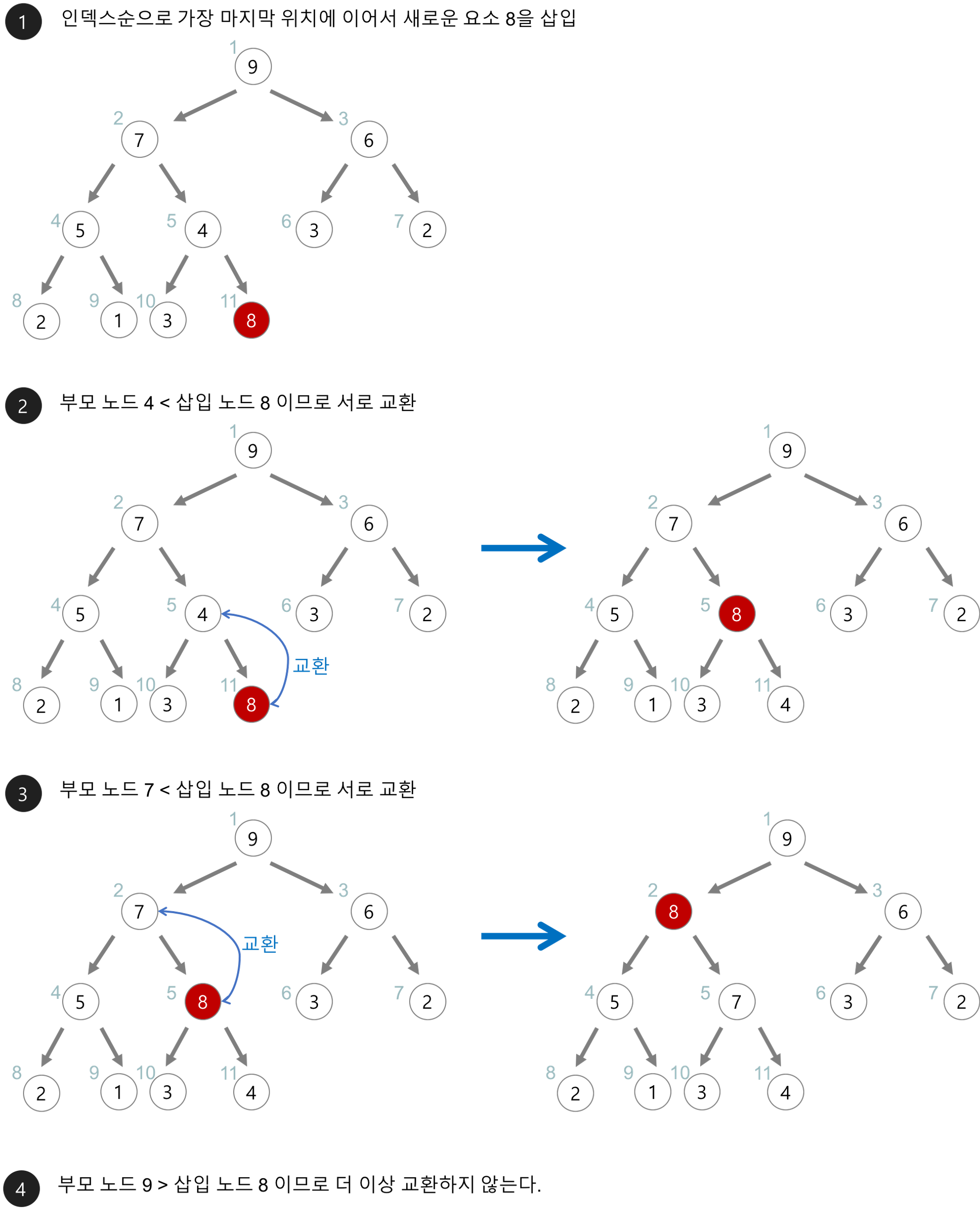
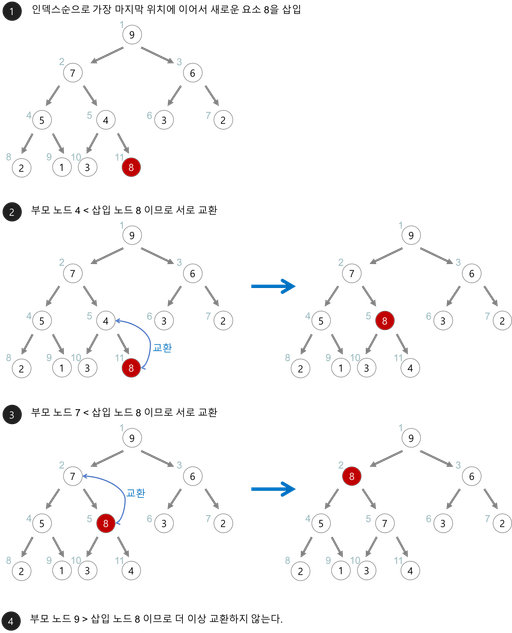
(8) 항목 삽입하기
// 항목 삽입하기(흘러 올리기(Percolate Up)
void Insert(Heap* h, int data)
{
int i;
if (h->count == h->capacity)
ResizeHeap(h);
h->count++; // 새 항목을 저장하기 위해 힙의 크기를 증가시킨다.
i = h->count - 1;
while (i >= 0 && data > h->array[(i - 1) / 2]) {
h->array[i] = h->array[(i - 1) / 2];
i = (i - 1) / 2;
}
h->array[i] = data;
}
void ResizeHeap(Heap* h)
{
int* array_old = h->array;
h->array = (int*)malloc(sizeof(int) * h->capacity * 2);
if (!h->array) {
printf("Memory Error\n");
return;
}
for (int i = 0; i < h->count; i++)
h->array[i] = array_old[i];
h->capacity *= 2;
free(array_old);
}
C
복사
(9) 힙을 제거하기
// 힙을 제거하기
void DestroyHeap(Heap* h) {
if (!h)
return;
free(h->array);
free(h);
h = NULL;
}
C
복사
(10) 배열을 힙으로 만들기
// 배열을 힙으로 만들기
void BuildHeap(Heap* h, int A[], int n) {
if (!h)
return;
while (n > h->capacity)
ResizeHeap(h);
for (int i = 0; i < n; i++)
h->array[i] = A[i];
h->count = n;
for (int i = (n - 1) / 2; i >= 0; i--)
PercolateDown(h, i);
}
C
복사
(11) 힙 정렬
// 힙 정렬
void Heapsort(int A[], int n) {
Heap* h = CreateHeap(n,1);
int tem;
BuildHeap(h, A, n);
for (int i = n - 1; i >= 0; i--) {
tem = h->array[0]; // h->array[0]이 가장 큰 항목이다.
h->array[0] = h->array[--h->count];
A[i] = tem;
PercolateDown(h, 0);
}
DestroyHeap(h);
}
C
복사