•
42실리콘벨리에서 처음 본과정 교육생이 되었을 때의 일이다. 거기에는 내가 이후에 등록할 수 있는 알고리즘 프로젝트들이 있었다. 나는 본과정에서 그 프로젝트들과 씨름하면서 고생하게 되리라고 일찌감치 알게 되었다.
그 중 하나가 바로 Push_swap 이다. 발상 자체는 간단하다. 두 개의 스택인 Stack A와 Stack B가 주어지는데, Stack A 는 정렬이 되어있지 않은 숫자들로 이루어진 임의의 리스트가 들어온다. 여러분은 Stack A 에 있는 정렬되지 않은 숫자들을 가지고, Stack A 에 이 숫자들 모두를 작은 수부터 시작해서 큰 수까지 오름차순으로 정렬해야 한다. 스택을 다루기 위해서는 몇 가지 허용된 액션 (Action) 만을 이용해야만 한다. 이 프로젝트의 주된 목적은 주어진 Stack A 를 가능한 한 액션을 적게 수행하여 정렬하는 것이다.
그렇다면 두 개의 스택에 어떤 액션을 할 수 있을까?
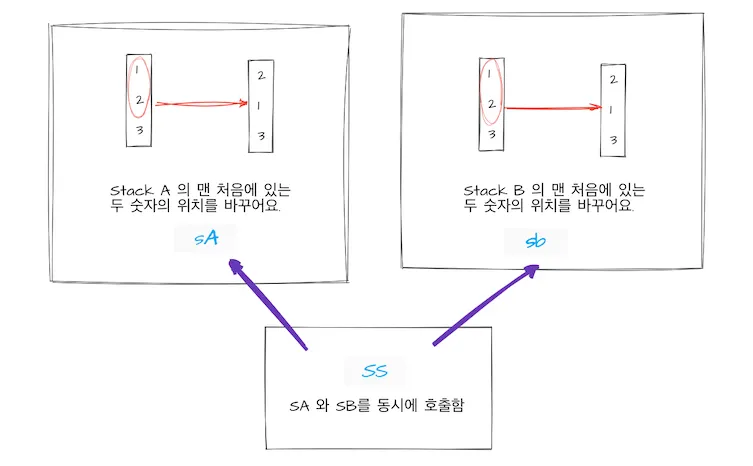
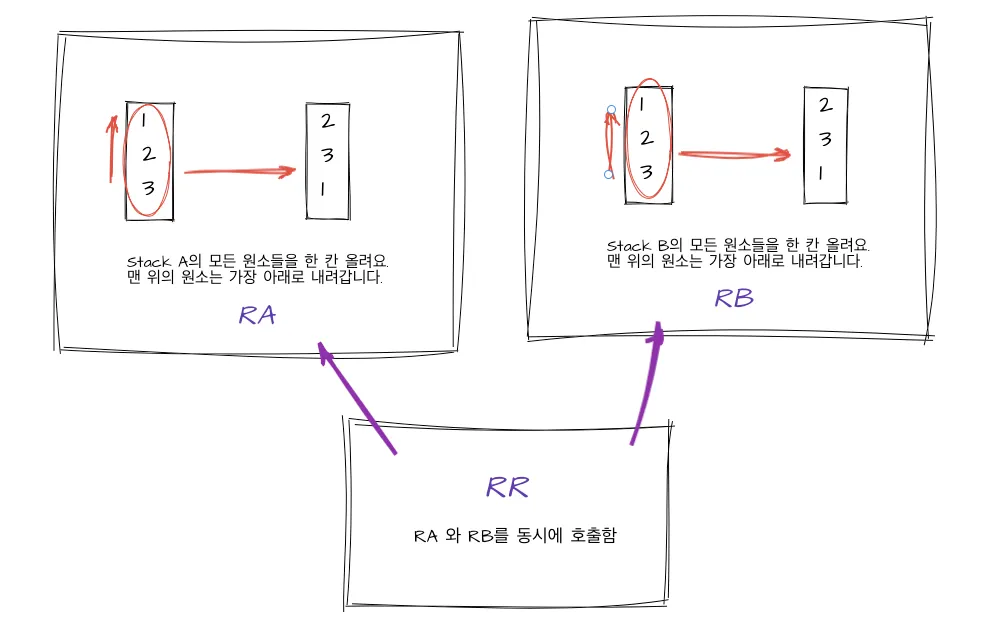
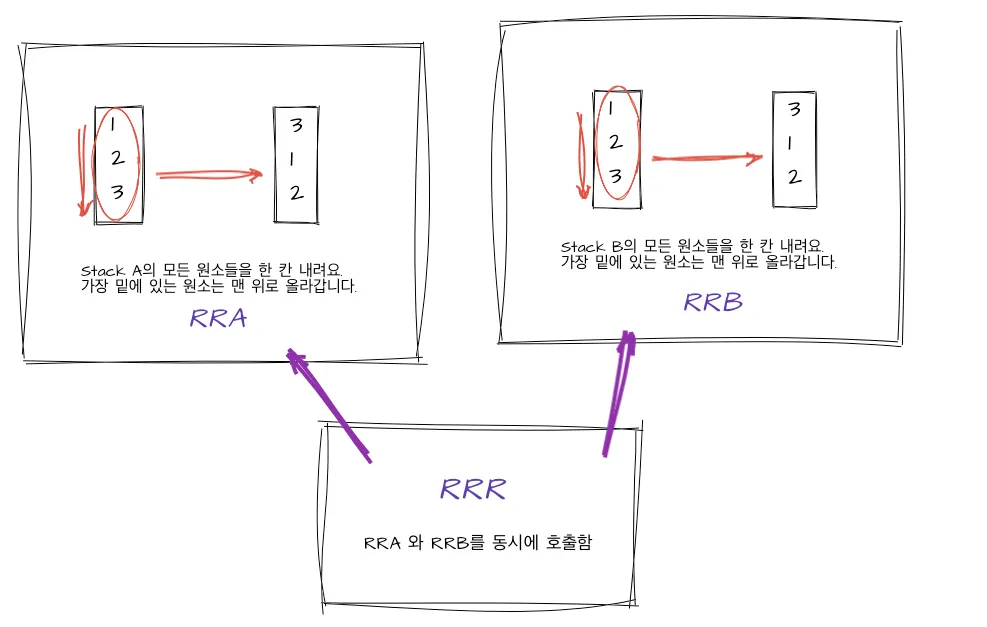
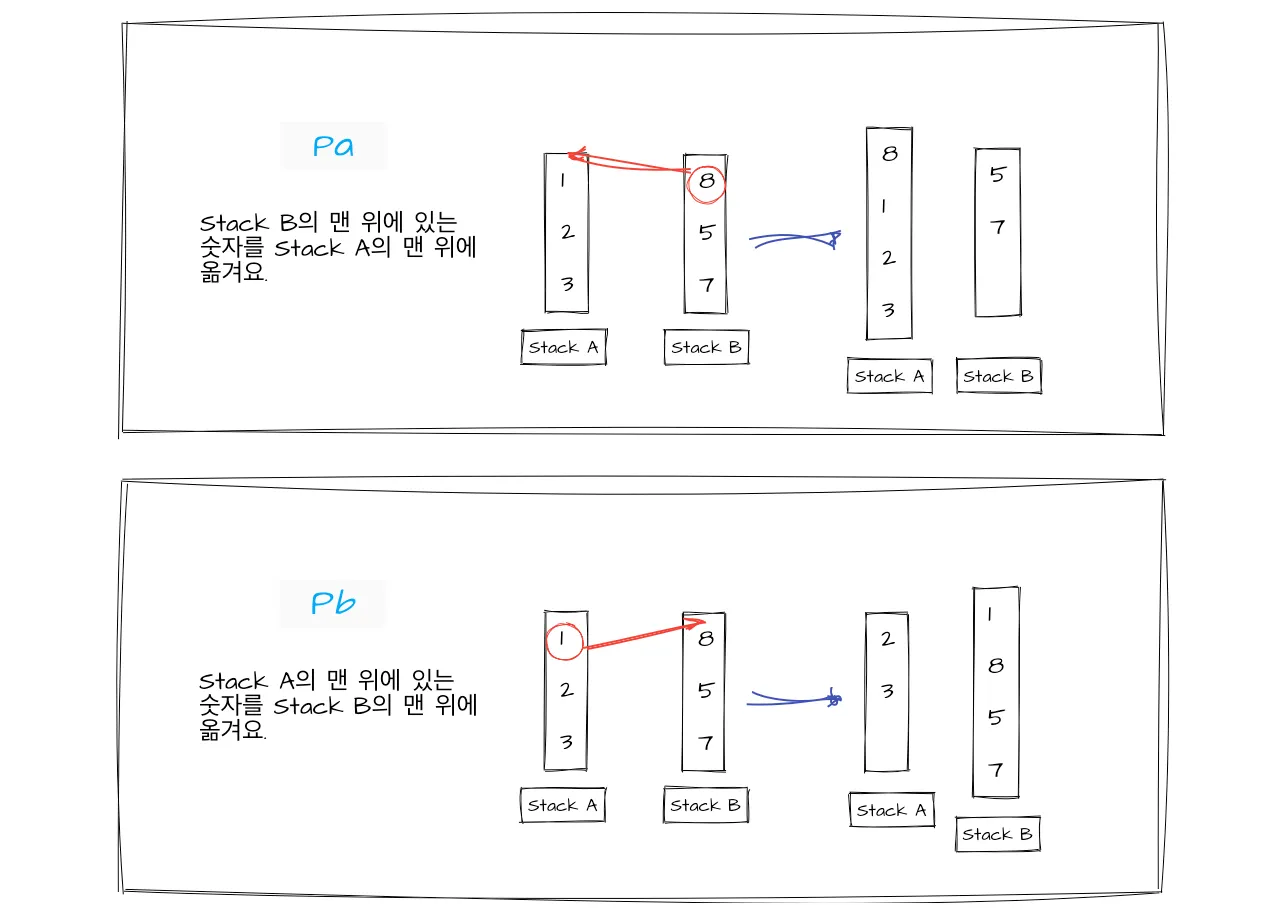
과제에서는 다음과 같은 액션들이 있다. : sa, sb, ss, ra, rb, rr, rra, rrb, rrr, pa, pb
이 액션들은 아래와 같이 동작한다.
그러면 이제 우리가 다룰 수 있는 액션을 알아보았으니, 이를 어떻게 써먹어야 할 지 알아보자. 우리가 구현하게 될 알고리즘은 얼마나 많은 임의의 수가 Stack A에 들어오는 지에 따라 달라지게 된다. 여기에서 나는 4가지 주요 케이스를 다루어보고자 하는데, 스텍에 각각 3, 5, 100, 500 개의 수가 들어오는 케이스를 살펴볼 것이다. 각 케이스들은 저마다 다르게 문제를 처리하도록 요구하기 때문에, 이에 대해 어떻게 최적화를 하여 접근했는지 케이스를 나누어서 살펴볼 것이다.
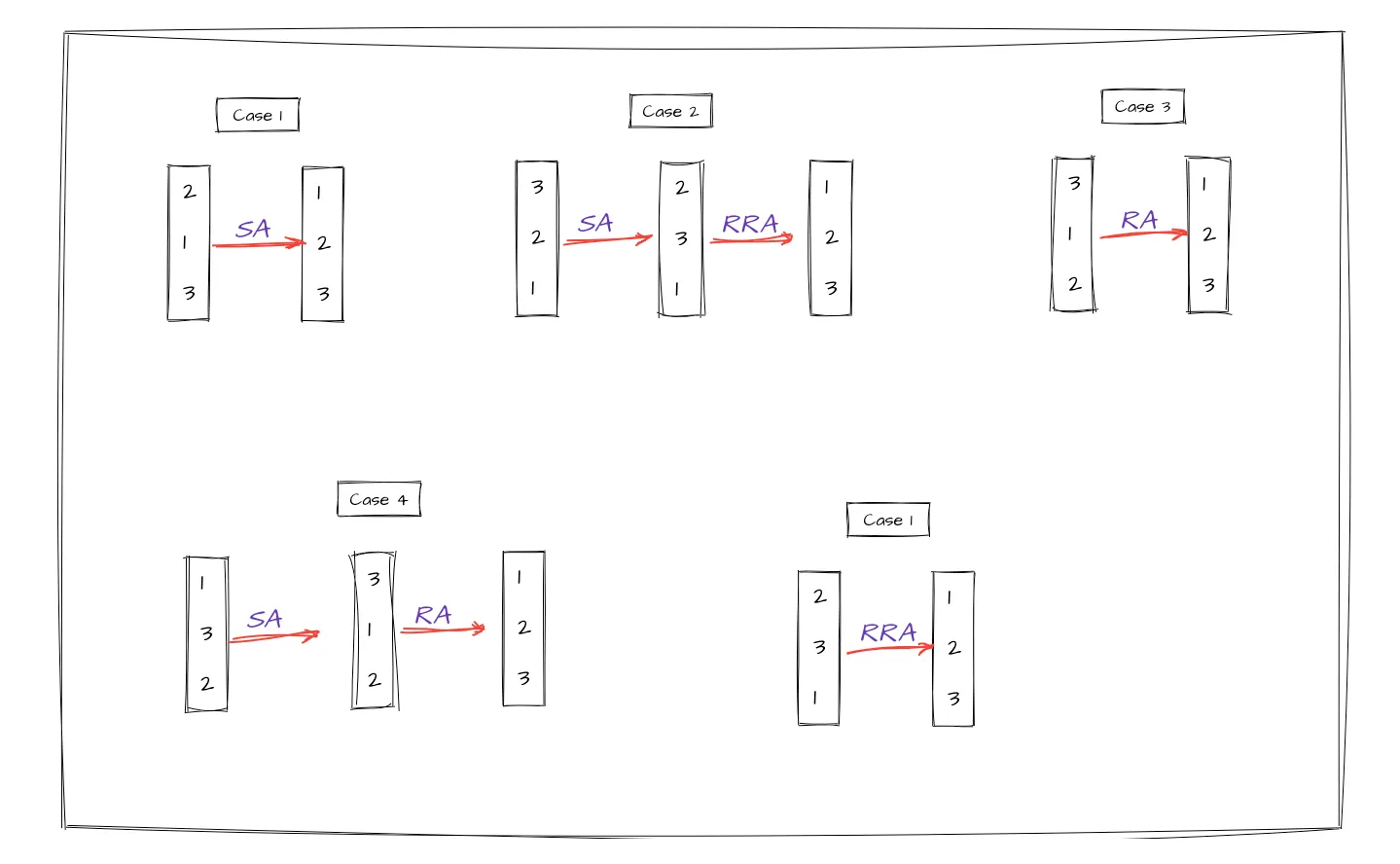
Stack A에 임의의 3개의 수가 들어올 때
Stack A에 임의의 3개의 수가 들어올 경우, 생길 수 있는 5가지 케이스를 생각해보았다. 먼저 이를 오름차순으로 액션을 3번 이상 쓰지 않고 정렬해보고자 했다. 어떤 액션을 가져다 쓸 지는 위, 아래, 중간 세 개의 숫자가 각각 어떠한 지에 따라 달라진다. 모든 케이스마다 나는 위와 중간, 중간과 아래, 아래와 위에 있는 숫자를 서로 비교하였다. 이 숫자들이 어떤 것이 작고 큰 지에 따라 호출되는 액션에 영향을 미쳤다.
Stack A에 임의의 5개의 수가 들어올 때
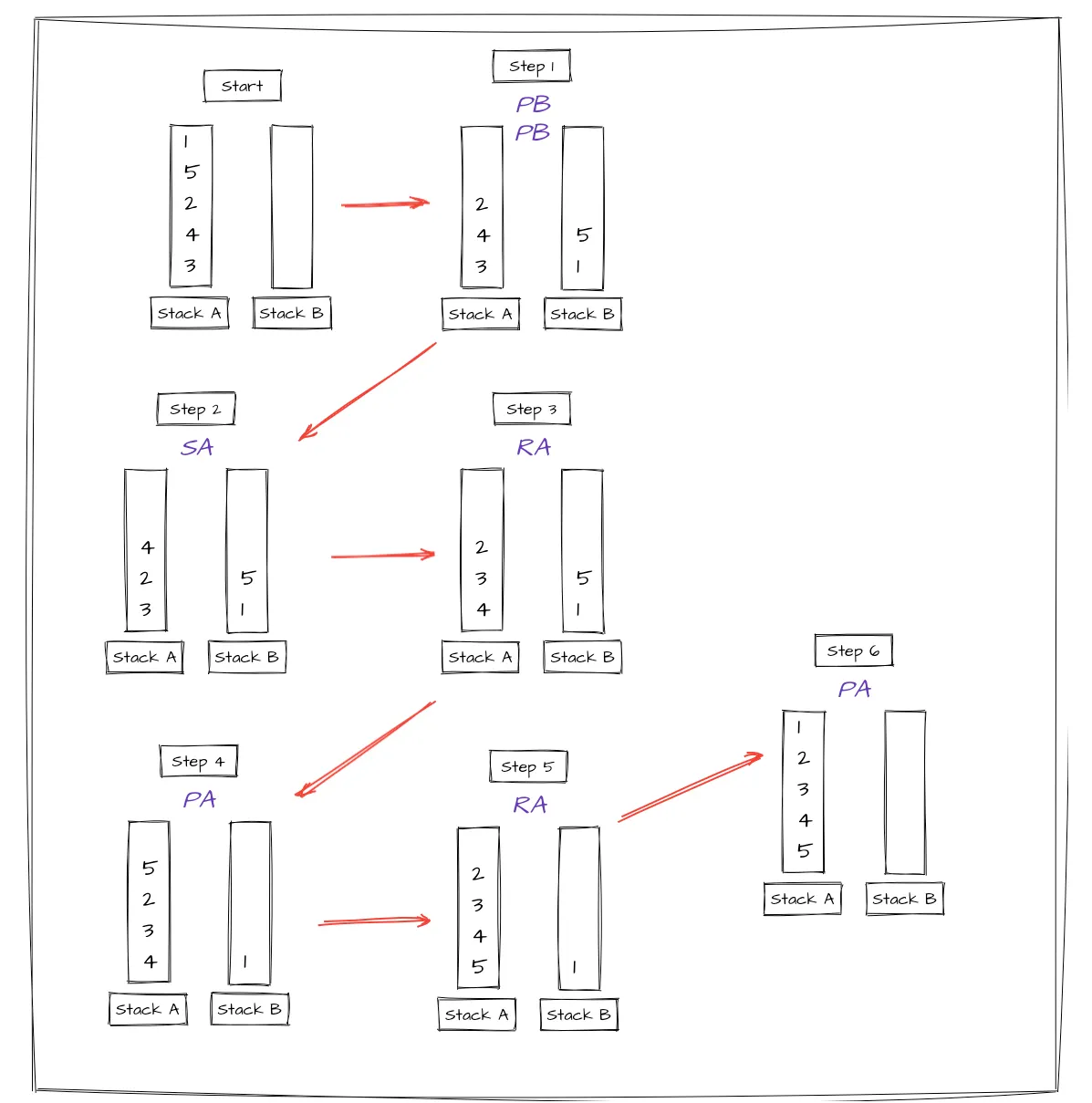
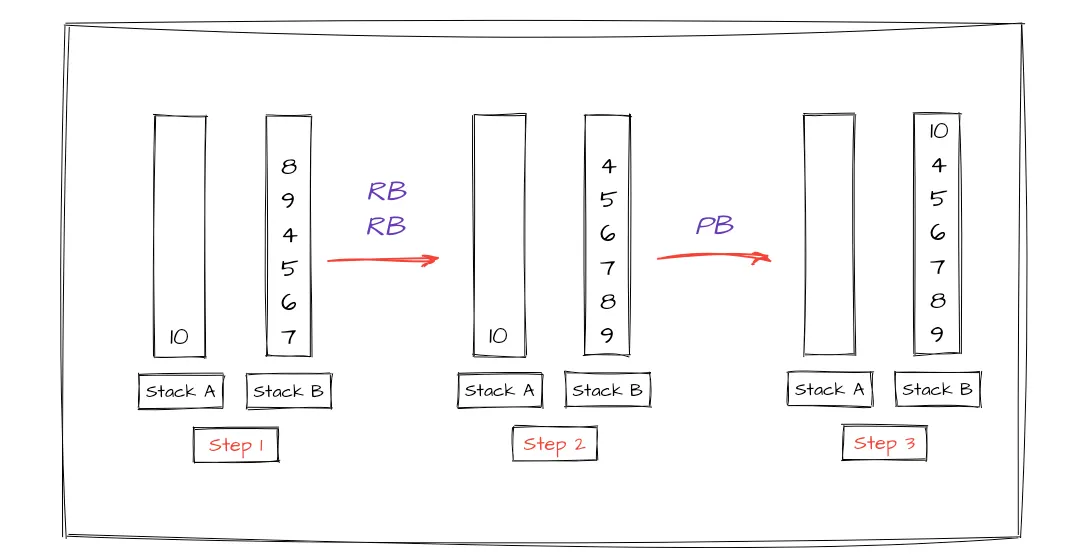
이제 Stack A에 들어온 5개의 임의의 수를 제한된 12가지의 액션으로 정렬해보자. 이 이상의 선넘는 액션을 하게되면 fail을 받을 것이다. 우리가 주목할 부분은 바로 위에서 다루었던 "Stack A에 임의의 3개의 수가 들어올 때" 사용한 알고리즘을 응용해 볼 수 있다는 것이다. 그저 우리는 Stack A의 다섯 개의 수 중 맨 위의 두 개의 숫자만 Stack B로 옮기고 문제를 해결하면 된다. 그러고 난 후 Stack A에 있는 모든 수를 정렬하고 Stack B로 옮겼던 두 수를 가져오면 되는 것이다. 금방 소개한 로직이 어떻게 적용되는지 [ 1 5 2 4 3 ]이 Stack A 로 들어올 때를 가정하여 적용해보자.
1단계 : 맨 위에 있는 두 숫자를 Stack A에서 Stack B로 보낸다.
2-3 단계 : **"Stack A에 임의의 3개의 수가 들어올 때"**에 사용한 알고리즘으로 Stack A를 정렬한다.
4-6 단계 : Stack B에 있는 두 숫자를 Stack A 로 가져와서 맨 위의 숫자와 비교하여 크고 작은지 확인한 후 적절한 위치에 배치한다.
이렇게 하면 제한된 12가지의 액션 중에서 원하는 액션을 선택하여 단 7번만 사용하면서 문제를 해결할 수 있다.
Stack A에 임의의 100개의 수가 들어올 때
처음에 이 케이스를 해결해보려고 했을 때, 나는 그저 선택정렬을 사용할 수 있을 거 같다고 생각했다. 과정은 매우 간단했었다.
1.
Stack A에서 가장 작은 수를 찾는다.
2.
Stack A에서 찾은 가장 작은 수를 Stack A의 맨 위로 올린다.
3.
이를 Stack B로 옮기고
4.
1-3까지의 과정을 Stack A에 아무런 숫자가 남아있지 않을 때까지 반복한다.
5.
Stack B에는 Stack A에 있던 모든 수가 내림차순으로 정렬되어 있으니, 이를 다시 Stack A로 불러온다.
Stack A에 있는 가장 작은 수를 Stack B로 보내는 것을 이용해서, Stack B에 모든 숫자가 큰 숫자부터 작은 숫자까지 내림차순으로 정렬되도록 할 수 있었다. 그런 뒤 모든 숫자를 다시 Stack A로 되보냈다. 이렇게하면 숫자들이 Stack A에 오름차순으로 정렬되도록 할 수 있을 것이다.
이 방법 자체는 일단 작동하기는 작동한다. 내 말은, 그러니깐 일단 숫자들을 정렬하는 알고리즘 자체는 문제가 없다는 뜻이다. 하지만, 프로젝트를 통과하기 위한 기준에 맞추어 최적화를 하는데엔 한참이나 뒤떨어진 것이다.
그러면 이를 최적화하려면 어떻게 해야할까? 생각을 하다가 내가 숫자 100개가 뭉친 하나의 큰 숫자 덩어리(Chunk)를 한 번에 정렬하고 있었음을 알아차렸다. 이를 각각 숫자 20개로 이루어진 5개의 작은 덩어리로 나눌 수 있었다.
Chunk 1에는 0-19까지
Chunk 2에는 20-39까지
...
Chunk 5에는 80-99까지의 숫자가 담긴다고 가정하자.
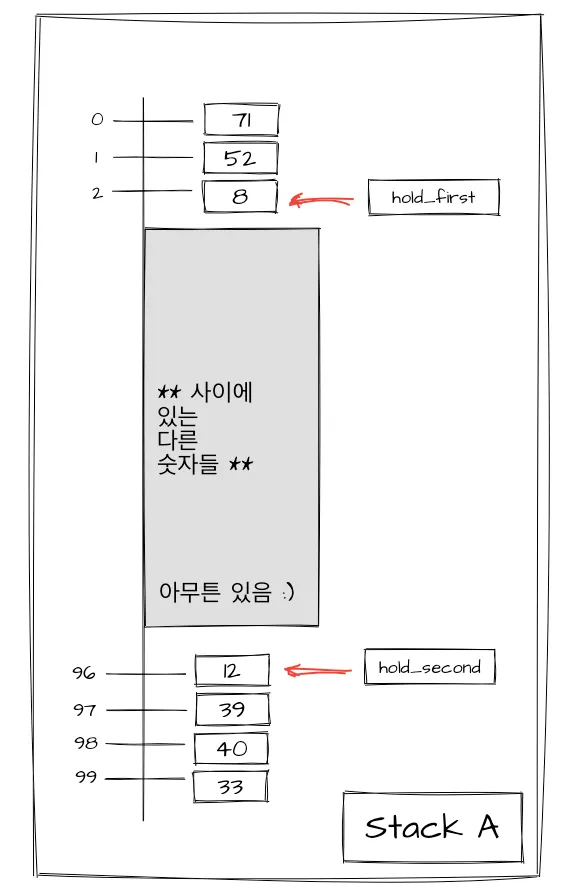
1단계 : Stack A를 맨 위에서부터 각 인덱스를 조회해서, 해당 숫자가 Chunk 1에 포함되는 숫자인지 확인한다. 만약 확인이 된다면, 이를 hold_first라고 하자.
2단계 : Stack A를 맨 밑에서부터 각 인덱스를 조회해서, 서로 다른 해당 숫자가 Chunk 1에 포함되는 숫자인지 확인한다. 만약 확인이 된다면, 이를 hold_last라고 하자.
3단계 : 이제 Chunk 1에 포함되는 hold_first와 hold_last두 숫자의 위치를 확인했으니, 두 숫자 각각 Stack A의 맨 위로 오기 위해서 몇 번 움직여야 하는지 서로 비교해본다.
두 숫자를 찾게되는 예제를 가정해보자. 위의 예제에서 숫자 8과 12는 Stack A에 있는 숫자인 동시에 Chunk 1에 포함되는 숫자이다. 두 숫자를 비교해보고 나면, 숫자 8을 Stack A의 맨 위로 올리기 위해 ra를 2번 실행하면 된다는 사실을 알 수 있다. 반대로 12의 경우에는 rra를 4번 실행해야 한다. 숫자 8이 12보다 더 적은 실행으로 Stack A의 맨 위로 올릴 수 있으니, 8을 우선적으로 Stack A의 맨 위로 보내보도록 하자.
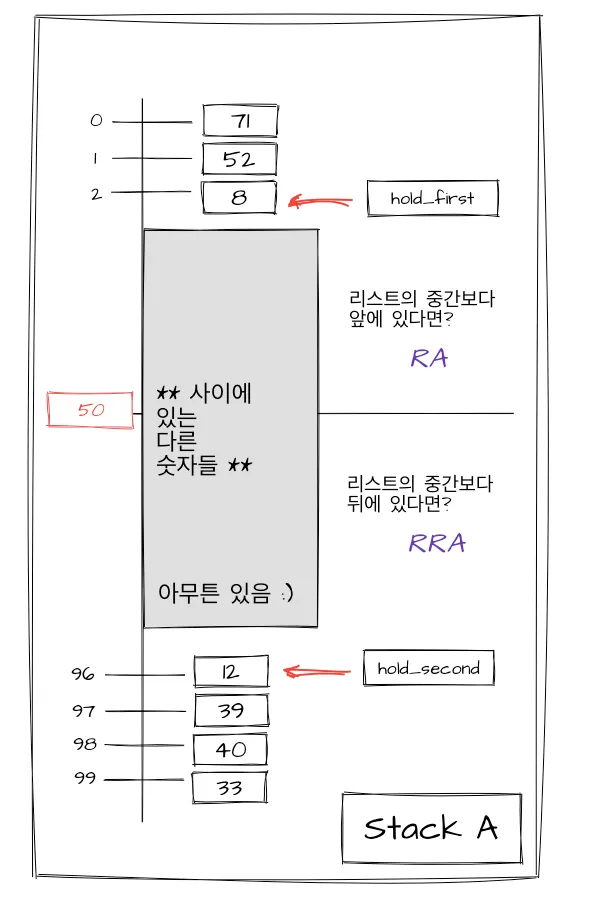
4단계로 넘어가기 전에, 위의 두 숫자를 위로 올리기 위해 ra 와 rra 가 왜, 몇 번이나 필요한지 알아낸 방법을 설명하려고 한다. 이를 위해, 기초적인 수학을 활용해보았다.
먼저 100개로 이루어진 리스트가 있다고 하자. 이를 2로 나누면, 50을 리스트의 정 가운데로 취할 수 있을 것이다. 그런 다음 내가 찾은 숫자가 어느 위치에 있는지 확인한다. 위의 예제에서 숫자 8은 2번 인덱스에 있는 것을 확인할 수 있다 (리스트의 맨 위의 숫자는 0번 인덱스에 위치한다. 맨 위에 있는 숫자는 리스트의 맨 위로 가기 위해 0번 움직여야 하니). 그러면 숫자 8이 위치하는 곳이 리스트의 절반인 50보다 큰지 작은지 알 수 있다. 숫자 8이 위치한 2번 인덱스의 2는 50보다 작으니, 숫자 8을 맨 위로 옮기기 위해서는 rra보다는 ra가 더 적게 실행하면서 리스트의 맨 위로 숫자 8을 가져다 놓을 수 있음을 알 수 있다.
반대로 12의 경우에는 96번째 인덱스에 위치하므로, 96은 50보다 크니, rra를 실행하는 것이 더 낫다는 것이다.
4단계 : 이제 원하는 숫자가 Stack A의 맨 위에 있으니, 이를 Stack B로 옮겨주도록 하자. 하지만 Stack B로 넘겨주기 전에 확인해야할 것이 있다. Stack B로 숫자를 옮겨 줄 때에 매번 가장 작은 수만 넣어주는 것은 아니기에, Stack B에 이미 들어와 있는 다른 숫자들보다 크진 않는지 확인해야 한다. 옮기는 숫자가 적절한 위치에 들어가도록 하기 위해서 로직을 짤 때에 무한루프를 만들지 않도록 주의하자.
위의 예제에서 숫자 10 을 올바른 위치에 옮겨주는 가장 빠른 방법은, Stack B에서 가장 작은 숫자를 찾아 그 수를 Stack B의 맨 위에 올려놓는 것이다. 그런 후에 숫자 10 을 Stack 의 맨 위에 옮겨놓을 수 있을 것이다.
5단계: Chunk 1의 범위에 포함되는 모든 숫자가 Stack A 에 없을 때까지 1-4까지의 과정을 반복해서 수행한다.
6단계: Chunk 1이 끝나고 나면, 나머지 Chunk 에 대해서도 1-4의 과정을 반복하여 Stack A의 모든 숫자가 Stack B로 옮겨지도록 하자.
7단계: 이제 Stack A가 비었으니, Stack B에서 가장 큰 숫자를 찾도록 하자. 이를 찾은 후 Stack B 의 맨 위로 올린 후 Stack A로 가져오자. 이 작업을 Stack B가 전부 비어질 때까지 반복한다. 이를 최적화하기 위해 3단계에서 ra rra 중 무엇을 사용할 지 판별하던 방법을 가져와서 사용할 수 있을 것이다.
이렇게 하면 Stack A에 원하는 대로 모든 숫자가 오름차순으로 정렬이 되어 있을 것이다.
Stack A에 임의의 500개의 수가 들어올 때
이건 다른 문제들 보다는 쉬울 것인데...
"**Stack A에 임의의 100개의 수가 들어올 때"**와 똑같은 로직을 사용하면 된다. 단, 이번에는 5개의 Chunk가 아니라 11개의 Chunk로 나누어서. 왜 하필 11이냐면...
몇 번 테스트를 돌려보고 난 뒤에 11로 결정하였는데, 11로 하는 것이 액션을 실행하는 횟수를 가장 적게 할 수 있었기 때문이었다.
도움이 될 만한 툴 :
아래의 링크에 있는 push_swap visualizer는 정말 강추한다. 이 시각화 툴은 push_swap 프로젝트를 위해 만들어졌는데, 코드를 최적화하면서 많은 도움을 받았다.