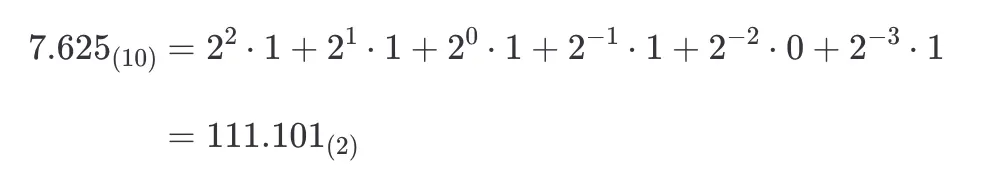10진수를 N진수로 바꾸는 방법
10진수는 10의 거듭 제곱의 합으로 이루어져있다. 예를 들어 123.4는 "10^2 * 1 + 10^1 * 2 + 10^0 * 3 + 10^-1 * 4" 이다.
같은 원리로 101.01은 "2^2 * 1 + 2^1 * 0 + 2^0 * 1 + 2^-1 * 0 + 2^-2 * 1" 이다.
*주의할 점
0.3을 2진수로 바꿔보자. 그러면 0.0100110011… 의 순환소수를 얻을 수 있다.
이 때 이 이진수를 정확하게 컴퓨터가 저장하려면 정말 무한한 양의 메모리가 필요하다. (이는 물리적으로 불가능하며 그렇게 할 필요도 없다.)
고정 소수점
고정 소수점은 정수를 표현할 비트 수와 소수를 표현할 비트 수를 미리 정해줍니다. 32비트로 소수를 표현한다고 가정합시다.
•
첫 1비트: 부호를 나타내는 비트입니다. (양수는 0, 음수는 1을 의미합니다.)
•
다음 15비트: 정수부를 나타내는 비트입니다.
•
다음 16비트: 소수부를 나타냅니다.
•
정수부와 소수부의 경계가 소수점의 위치입니다.
예를 들어, 10진수 7.625를 32비트 고정 소수점으로 표현해보겠습니다. 먼저 10진수 7.625를 2진수로 표현하면 다음과 같습니다.
이를 비트 고정 소수점 방식으로 표현하면 다음과 같습니다.
한계
고정 소수점이 표현할 수 있는 실수는 한계가 있다. 왜냐하면 정수는 15비트로, 소수는 16비트 안에서 표현해야 하기 때문이다.
그러므로 이를 벗어나는 수를 고정 소수점 방식으로 표현하려고 시도하면 ‘정밀도(?)’가 떨어진다.
*정밀도: 정보 손실 없이 나타낼 수 있는 유의한 자릿수 (표현할 수 있는 비트 수 정도로 이해하고 있음)
부동 소수점
소수점이 옮겨 다니는 실수 표현법이다.
부동 소수점이 비트를 사용하는 방법과 고정 소수점이 비트를 사용하는 방법이 다릅니다.
그리고 부동 소수점의 비트 체계 중 가장 널리 쓰이는 표준은 IEEE 754 라고 합니다.
이에 따르면 실수를 다음과 같은 부동 소수점 표현 방식으로 나타낼 수 있습니다.
1.
2진수를 정규화 합니다.
2.
처음 1비트는 부호를 나타냅니다.
3.
다음 8비트는 지수부를 나타냅니다. 정규화 과정에서 얻은 지수에 bias를 더한 값으로 채웁니다.
4.
다음 23비트는 가수부를 나타냅니다. 소수 부분의 값으로 채웁니다.
5.
채워지지 않은 비트를 모두 0으로 채웁니다.
정규화
실수를 1.xx * 2^n의 꼴로 나타내는 것을 정규화라고 합니다.
이 때 N은 지수로, .xxx 는 가수부를 의미합니다.
10진수 7.625를 정규화 해봅시다.
이를 2진수로 바꾸면 111.101 입니다. 그리고 나서 정규화를 하면,
1.11101 * 2^2 입니다. 여기서 지수는 2입니다.
Exponent (지수부)
IEEE 724 표준에서는 32비트를 실수로 표현할 때 127이라는 bias를 지수에 더한 값으로 exponent(지수부)를 채우라고 명시하고 있습니다.
즉, 위의 예시에의 지수는 129 (2 + 127) 로 지수부에 저장됩니다.
왜 bias라는 값을 따로 두었을까요? 그 이유는 지수가 음수일 경우를 대처하기 위해서 입니다.
예를 들어 0.000101 라는 2진수를 정규화하면 1.01 * 2^-4 라는 값을 얻게 됩니다.
위의 예시와 다르게 지수가 음수로 나왔습니다.
그렇다면 지수가 음수인 것을 어떻게 비트로 나타내야 할까요?
가장 간단한 아이디어는 전체 수가 양수인지 음수인지를 나타내는 부호 비트를 할당한 것 처럼,
지수가 음수인지 양수인지를 표현하는 비트를 새로 할당하는 것입니다.
그러나 이 경우 표현할 수 있는 수의 범위가 작아진다는 단점이 있습니다.
127은 0~255 구간의 딱 절반에 해당하는 숫자입니다. 10진수를 기준으로
•
0 ~ 127 구간은 음수 (실제 지수는 -127 ~ 0)
•
128 ~ 255 구간은 양수 (실제 지수는 0 ~ 128)
참고로 0과 255는 각각 0과 무한대 등을 나타내기 위해 특별히 할당된 숫자이기 때문에 앞서 설명드린 정규화 방법이 적용되지 않는다고 합니다.
Mantissa
Mantassia는 고정 소수점의 fractional part와 같은 역할입니다.
정규화 결과에 따라 소수 부분을 mantassia 자리에 그대로 넣고, 남는 자리는 0으로 채웁니다.
7.625를 부동 소수점으로 표현해보겠습니다.
•
2진수 변환: 111.101
•
정규화 : 1.11101 * 2^2
•
지수부: 2 + 127 = 129 = 10000001
•
가수부: 11101
부동 소수점의 장 단점
부동 소수점은 고정 소수점에 비해 더 큰 범위를 표현할 수 있습니다.
예를 들어 고정 소수점은 정수 부분에 15개의 비트를 사용한다고 말씀 드렸는데요.
이는 총 2^15 개의 정수를 표현할 수 있다는 것입니다.
그렇다면 부동 소수점은 얼마나 큰 범위의 정수를 표현할 수 있을까요?
부동 소수점은 지수부에 8비트를 사용합니다.
8비트로 채울 수 있는 가장 큰 숫자는 11111111 이지만,
부동 소수점 표현에서 이는 무한대의 숫자를 나타내는 특별한 수이므로 실질적으로 가장 큰 숫자는 11111110 입니다.
이를 10진수로 바꾸면 254입니다.
254는 bias 127이 더해져 있죠. 따라서 정규화 결과로 가질 수 있는 가장 큰 지수는 127입니다.
부동 소수점은 고정 소수점에 비해 거 큰 범위의 값을 저장할 수 있는 장점이 있습니다.
그헣다면 부동 소수점의 단점은 없을까요? 실수 연산이 부정확할 수 있습니다.
이는 컴퓨터 하드웨어가 가지는 본질적인 한계점 때문에 완벽하게 극복할 수는 없습니다.
예를 들어 십진수 0.3을 2진수로 변환하면 0.0100110011 … 처럼 특정 수가 무한히 반복됩니다.
따라서 컴퓨터가 가지는 지수부, 가수부를 다 써도 정확하게 표현할 수 없습니다.
이는 근사치로 표현됩니다.
부동 소수점 연산
2진수 소수 표현법
•
sign : 부호 표시
•
significand: 유효 숫자
•
exponent: 지수
부동 소수점의 덧셈과 뺄셈
1.
지수를 같게 조정한다. (작은 쪽을 큰 쪽에 맞춘다.)
2.
연산을 수행한다.
3.
계산 결과를 정규화한다.
부동 소수점의 곱셈
1.
가수끼리 곱한다.
2.
지수끼리 더한다.
3.
정해진 소수이하 자리에서 반올림한다.
4.
계산 결과를 정규화한다.
부동 소수점의 나눗셈
1.
가수끼리 곱한다.
2.
지수끼리 뺀다.
3.
정해진 소수이하 자리에서 반올림한다.
4.
계산 결과를 정규화한다.