목차
동적 계획법 (Dynamic Programming) 이란?
동적 계획법은 하나의 큰 문제를 여러 개의 작은 문제로 나누고, 작은 문제를 해결한 결과를 저장하여 큰 문제를 해결할 때 사용하는 문제 해결 패러다임이다.
동적 계획법이 필요한 이유?
일반적으로 재귀 함수의 불필요한 연산을 줄이기 위해서 동적 계획법을 사용한다.
재귀 함수도 이전의 결과값을 활용해서 다음 결과를 계산한다는 점에서 동적 계획법과 비슷하다. 하지만, 재귀 함수는 결과를 구한 동일한 문제에 대해 다시 계산을 하는 문제점이 있다.
대표적인 사례로 피보나치 수열이 있다. 피보나치 수열은 1번째 수는 0, 2번째 수는 1로 정의하고, 3번째 수 부터는 바로 앞의 두 수를 더한 값을 저장하는 것이다.
0, 1, 1, 2, 3, 5, 8, 13, ...
Plain Text
복사
이를 재귀 함수로 구현하면 다음과 같다.
const fibo = (n) => {
if (n <= 1) // 1번째 수와 2번째 수에 도달했을 때, 각각 0과 1을 반환
return n;
return fibo(n - 1) + fibo(n - 2);
}
JavaScript
복사
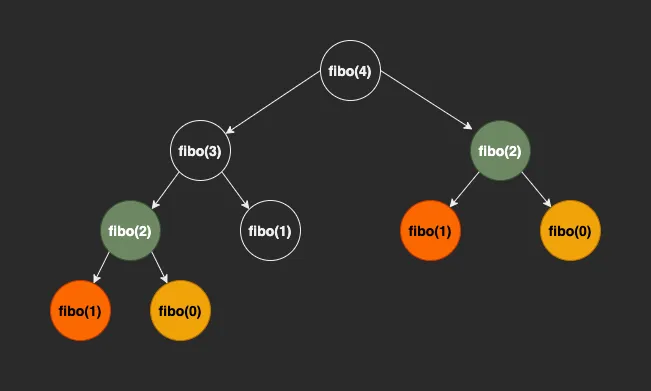
n = 4 라고 했을 때, 이다.
이때, 이다. 하지만, 의 결과는 구할 때와 를 구할 때 모두 필요한데, 결과값을 따로 저장하지 않아서 매번 계산을 다시 해주어야 한다. 이를 그림으로 표현하면 다음과 같다.
즉, 재귀 함수로 구현하면 동일한 값을 2번씩 구하게 되며, 시간 복잡도는 (f(4) = f(3) + f(2) + f(1) + f(0) + f(2) + f(1) + f(1)) 이 된다. 그래서 n 의 값이 커질 수록 연산이 기하급수 적으로 증가하는 문제가 생긴다.
이러한 재귀 함수의 문제 때문에 이미 계산을 마친 결과에 대해서는 값을 저장해놓고, 그 값을 다시 활용하여 연산을 줄이는 동적 계획법이 등장하게 되었다.
동적 계획법 구현하기
동적 계획법은 크게 2가지 방식으로 구현할 수 있다.
1.
Bottom-Up (Tabulation 방식) : 반복문 사용
2.
Top-Down (Memoization 방식) : 재귀 사용
1. Bottom-Up 방식
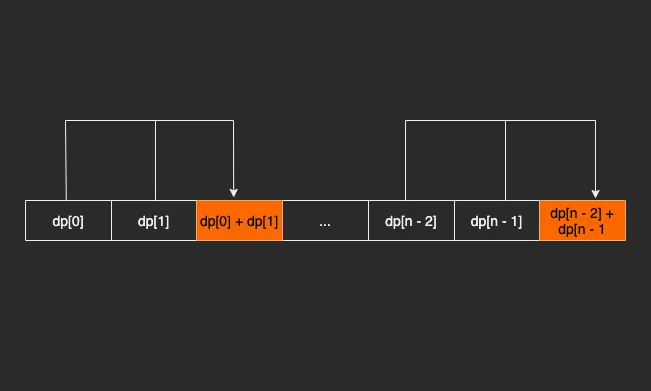
작은 문제의 결과부터 계산하고, 이 결과들을 누적해서 큰 문제를 해결하는 방식이다.
결과값을 저장하는 dp 라는 1차원 배열이 있다고 하자. 초기 상태인 dp[0] 부터 시작해서 반복문을 통해 목표값인 dp[n] 까지 반복문을 통해 점화식으로 결과를 재활용하는 방식이다.
참고로 이 방식을 “Tabulation 방식" 이라고 부르는 이유는 반복을 통해 테이블의 처음부터 마지막까지 채우는 과정을 “table-filling” 이라고 부르기 때문이다.
사실 이전 결과를 기억하고 다시 사용한다는 점에 있어 Memoization 과 개념적으로 크게 다르지는 않다.
피보나치 수열을 “Bottom-Up” 방식으로 구현하면 다음과 같다.
const bottom_up_fibo = (n) => {
const table = Array(n).fill(0); // 값을 저장하기 위한 테이블 선언
table[0] = 1; // 초기값 선언
table[1] = 2;
for (let i = 2; i < n; i++) {
table[i] = table[i - 1] + table[i - 2]; // 점화식을 통한 계산
}
return table[n - 1]; // 테이블의 마지막 요소에 저장된 값을 반환.
}
JavaScript
복사
2. Top-Down 방식
dp[n] 의 값을 찾기 위해 n 부터 호출을 시작하여 dp[0] 까지 도달하여 결과 값을 재귀를 통해 전달받는 방식이다.
이전에 계산을 완료한 경우에는 메모리에 저장된 내역을 참조하여 값을 찾아온다. 즉, 가장 최근 상태 값을 메모했다고 하여 “Memoization” 라고 한다.
의사 코드로 구현하면 다음과 같다.
const memo = Array(n + 1).fill(0); // 계산 결과를 저장하기 위한 배열 초기화
const top_down_fibo = (n) => {
// 초기값인 0과 1에 도달하는 경우
if (n < 2) {
memo[n] = n;
return n;
}
// 이미 계산된 결과가 있는 경우 해당 결과를 반환
if (memo[n] > 0)
return memo[n];
memo[n] = top_down_fibo(n - 1) + top_down_fibo(n - 2);
return memo[n];
}
JavaScript
복사
위의 코드에서 일반적인 재귀 함수와 다른 부분은 다음과 같다.
// 1. 이미 계산된 결과가 있는 경우 해당 결과를 반환
if (memo[n] > 0)
return memo[n];
// 2. 계산 결과를 배열에 따로 저장
memo[n] = top_down_fibo(n - 1) + top_down_fibo(n - 2);
JavaScript
복사
이와 같은 방식으로 시간 복잡도를 으로 줄일 수 있다.
분할 정복과 다른 건가?
분할 정복과 동적 계획법은 주어진 문제를 작게 쪼개어 하위 문제로 해결하고, 이를 바탕으로 큰 문제를 해결한다는 점에서는 같다.
하지만, 분할 정복은 분할된 하위 문제가 동일하게 중복이 일어나지 않는 경우에 사용하며, 중복이 일어나는 경우에는 동적 계획법을 쓴다.
연습 문제 (2 x n 타일링)
2 x n 타일링 문제는 동적 계획법의 대표적인 문제이다.
문제 설명
가로 길이가 2이고 세로의 길이가 1인 직사각형모양의 타일이 있습니다. 이 직사각형 타일을 이용하여 세로의 길이가 2이고 가로의 길이가 n인 바닥을 가득 채우려고 합니다. 타일을 채울 때는 다음과 같이 2가지 방법이 있습니다.
•
타일을 가로로 배치 하는 경우
•
타일을 세로로 배치 하는 경우
예를 들어서 n 이 7인 직사각형은 다음과 같이 채울 수 있습니다.
제한 사항
•
가로의 길이 n은 60,000이하의 자연수 입니다.
•
경우의 수가 많아 질 수 있으므로, 경우의 수를 1,000,000,007으로 나눈 나머지를 return해주세요.
문제 분석
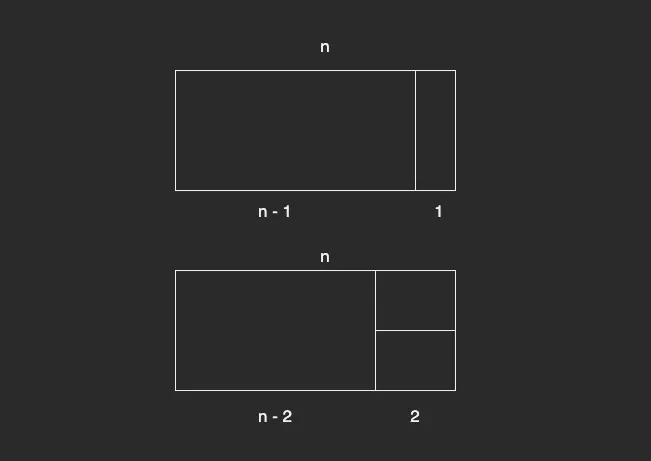
마지막에 놓는 타일은 가로가 1인 직사각형을 1개 배치하거나, 가로가 2인 직사각형을 2개 배치하는 방법이 있다. 그래서 가로의 길이가 n 인 직사각형을 만들기 위해서는 가로가 n - 1 인 직사각형을 만드는 경우의 수와 n - 2 인 직사각형을 만드는 경우의 수를 더한 것과 동일하다.
그렇다면 가로가 n - 1 인 직사각형을 채우는 경우의 수는 가로가 n - 2 인 직사각형을 채우는 경우의 수와 n - 3 인 직사각형을 채우는 경우의 수를 더한 것과 같다.
.png&blockId=fcdb4721-42f1-493a-9a9a-b6cf8e63e6cf)
즉, 관계가 성립한다는 것이다.
구현 코드
Bottom-Up 방식으로 구현한 코드는 다음과 같다.
function solution(n) {
if (n === 1 || n === 2)
return n;
const dp = Array(n).fill(0);
const mod = 1000000007;
dp[0] = 1;
dp[1] = 2;
for (let i = 2; i < n; i++)
dp[i] = (dp[i - 1] + dp[i - 2]) % mod;
return dp[n - 1];
}
JavaScript
복사
연산 결과를 저장할 1차원 배열 dp 의 길이를 n 으로 설정하고, 0 으로 초기화 한다.
그리고 n = 1 일 때 경우의 수인 1 과 n = 2 일 때 경우의 수인 2 를 배열의 가장 처음에 설정한다.
그 다음, 반복문을 돌며 점화식에 따라 연산을 수행한다.
참고로 연산 결과에 1000000007 로 나눈 나머지를 저장하는 이유는 경우의 수가 지나치게 많아지면 오버 플로우가 발생하기 때문이다. 그래서 오버 플로우가 발생하면 소수 1000000007 로 나눈 값을 결과로 받아서 처리하는 것이다.
그리고 Top-Down 방식으로 구현한 코드는 다음과 같다.
function solution(n) {
if (n === 1 || n === 2)
return n;
const memo = Array(n + 1).fill(0);
const mod = 1000000007;
const dp = (n) => {
if (n <= 2)
return n;
if (memo[n] > 0)
return memo[n];
memo[n] = (dp(n - 1) + dp(n - 2)) % mod;
return memo[n];
}
return dp(n);
}
JavaScript
복사
정확성 테스트는 전부 맞지만, 효율성 테스트에서 실패한다. 이는 JavaScript 가 Call Stack 의 최대 개수를 제한하는 언어이기 때문이다.
실제로 n = 60000 일때, JavaScript 로 실행하면 Maximum call stack size exceeded 오류가 발생한다.
그렇기 때문에 JavaScript 로 구현한다면 Bottom-Up 방식으로 구현하는 것이 좋다.
참고 자료
•
[BOJ] 11726 2xn타일링 Java 풀이 [티스토리]
