원래 글재주가 없다보니 설명이 매끄럽지 않을 수 있습니다. 미리 양해부탁드립니다!
mlx 메뉴얼 경로 : /usr/share/man/man3/mlx/
FDF
이 글을 쓰는 목적 자체가 해당 과제에 대해서 더 쉽게 이해하고 수월하게 접근하기 위해서 쓰는 것이기 때문에 mlx같은 부분은 생략하도록 하겠습니다!
•
과제 내용 : .fdf 파일을 읽어서 해당 맵의 모습을 윈도우에 띄워라!
ex)
fdf
작동 순서
1.
인자로 파일을 잘 받았는지 확인한다.
2.
mlx를 사용할 때 필요한 data를 초기화한다.(init_mlx)
3.
파일에 담긴 내용대로 image에 선을 그린다.(draw_map)
4.
계속 loop를 돌면서 이벤트가 발생하면 해당 이벤트에 맞춰 image를 다시 그린다.(cntl_map)
main.c
mlx용 구조체
FDF를 하면서 배운 것들
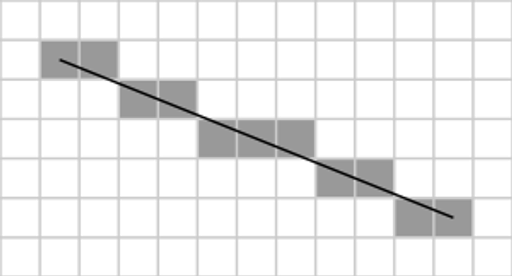
1. 브레젠험 알고리즘(Bresenham’s line algorithm)
fdf파일들은 각 점의 좌표들을 나타내고 있다. 그러면 두 점들을 어떻게 이어줘야 할까?
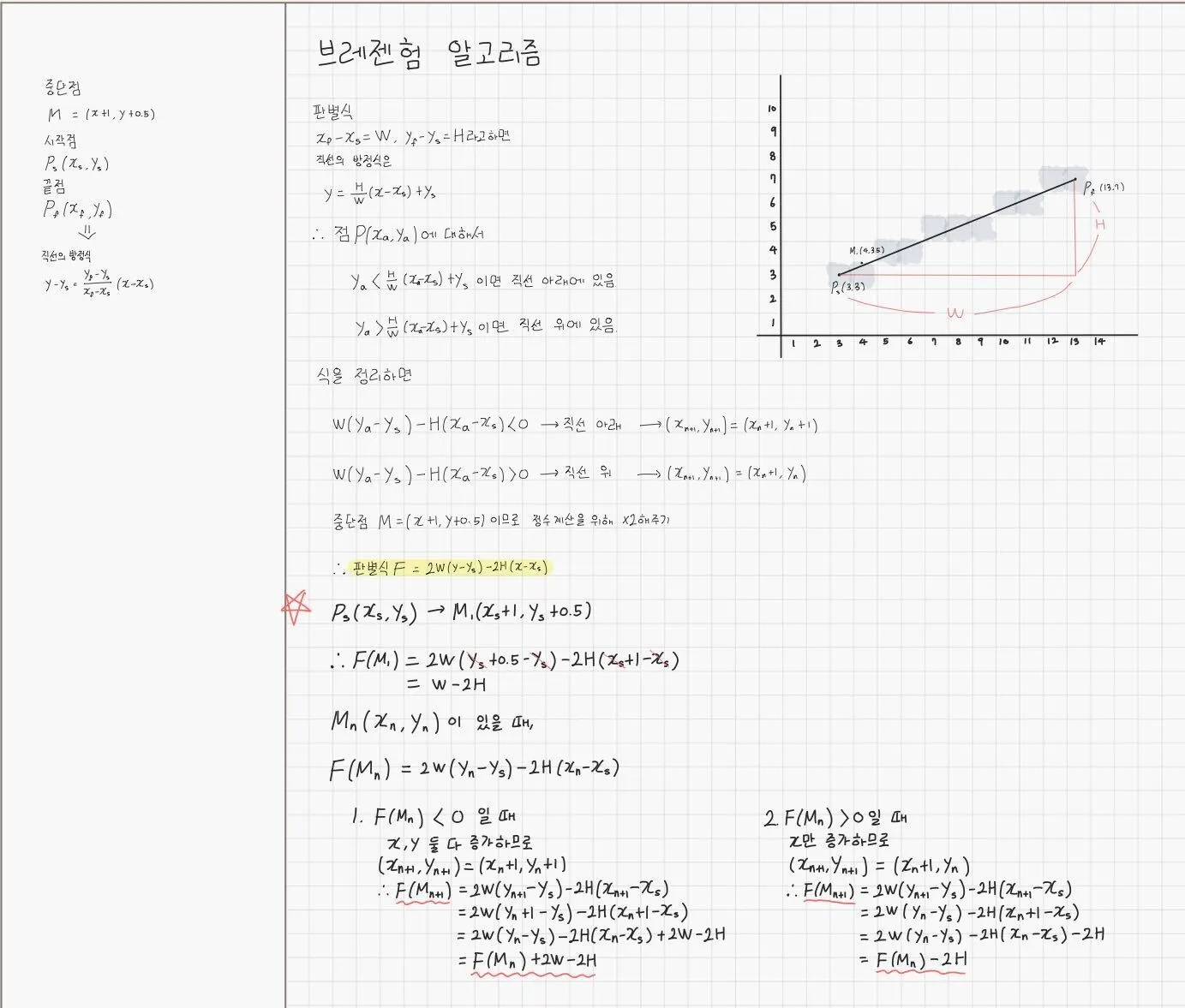
브레젠험 알고리즘 : 중단점을 기준으로 직선이 중단점 위에 있는지 아래에 있는지 확인하여 직선과 가장 가까운 정수값을 찾는 알고리즘.
•
x축과 y축 중에서 두 점의 차이가 큰 축을 기준으로 일정하게 증가시키면서 다른 축의 값을 증가시킬지 판단하면서 점을 찍는다.
◦
ex) 시작점이 (3, 3) 끝점이 (13, 7)이라면 x값의 차이는 10, y값의 차이는 4. → x값이 크므로 x값을 1씩 증가시키면서 y값을 증가시킬지 아닐지 판단.
◦
중단점 M = (x + 1, y + 0.5)
◦
중단점이 직선 위에 있으면 x값만 1증가, 직선 아래에 있으면 x, y값 둘 다 1증가. → 끝 점에 도달할 때까지 반복
.jpg&blockId=7e1db21f-8913-4a36-9079-ad67f50b7542)
H>W인 경우 반대로만 하면 된다.
코드 구현 - 1차(필기랑 판별식의 부호가 반대로 되어있으니 헷갈리지 않게 조심하자.)
알고리즘을 내용대로 구현했을 때 코드의 길이가 생각보다 많이 길다. 좀 더 찾아보다가 최적화한 알고리즘을 봤는데 이해하고 구현하기 쉽지 않았다. 반드시 해당 부분을 이해하고 구현해보았으면 좋겠다.
W > H | W < H | |
F(M1) | 2H - W | 2W - H |
F(M) < 0 | F(M+1) = F(M) + 2H (M = 직선 위/ x증가) | F(M+1) = F(M) + 2W (M = 직선 위/ y증가) |
F(M) > 0 | F(M+1) = F(M) + 2H - 2W (M = 직선 아래/ x, y증가) | F(M+1) = F(M) + 2W - 2H (M = 직선 아래/ x, y증가) |
M = 중단점
우선 판별식의 모습을 아래처럼 살짝 바꾼다.
W > H | W < H | |
F(M1) | W - 2H | 2W - H |
F(M) < 0 | F(M+1) = F(M) - 2H + 2W (M = 직선 아래/ x, y증가) | F(M+1) = F(M) + 2W (M = 직선 위/ y증가) |
F(M) > 0 | F(M+1) = F(M) - 2H (M = 직선 위/ x증가) | F(M+1) = F(M) + 2W - 2H (M = 직선 아래/ x, y증가) |
F(M1) = 2W - 2H로 두고
1) F(M) < W ——> W - 2H < 0(= 2H - W > 0)
2) F(M) > -H ——> 2W - H > 0
두 가지 조건식으로 나눈다.(이해하기 조금 어려울 수도 있어요…)
1.
W > H 인 경우
2번 조건 무조건 충족. x += x_value, F(M + 1) -= 2H
1번 조건 충족 시, y += y_value, F(M + 1) += 2W
2.
W < H 인 경우
1번 조건 무조건 충족. y += y_value, F(M + 1) += 2W
2번 조건 충족 시, x += x_value, F(M + 1) -= 2H
코드 구현 2차
생각보다 내용이 길어질 것 같아서 이번엔 여기까지만 정리하고 다음에 다른 내용으로 이어서 정리할게요!
제가 참고했던 사이트나 같이 보면 좋을 것 같은 내용 첨부할게요!
