cpp09의 마지막 문제의 핵심인 merge-insert sort algorithm, Ford-Johnson algorithm이 뭔지 알아보자.
ford-johnson algorithm
(“The Art of Computer Programming”의 해당 알고리즘에 대한 설명이 적힌 부분을 참조하였다.)
1. 비교횟수
우선 포드 존슨 알고리즘은 비교를 통한 정렬을 할 때(comparison sort) 정렬하기 위한 최소 비교 수에 대한 고민에서 시작되었다.
n개의 원소를 정렬하기 위해 충분한 최소 비교 수를 S(n)이라고 했을 때 S(n)은 nlgn보다 낮을 수 없다.
왜 비교 횟수가 O(nlgn)을 넘을 수 없는가?
“The Art of Computer Programming”
정렬의 하한
책에서 나온 가장 적은 비교가 필요한 정렬 방법은 binary insertion, tree selection, and straight two-way merging 세가지다. 세 가지 방법 모두 대략적으로 nlgn의 횟수를 가지고 있다.
binary insertion의 횟수를 B(n)이라고 하고, two-way list merging의 횟수를 L(n)이라고 했을 때,
아래 표는 n개의 원소가 있을 때 위에서 논의했던 방법들의 최대 비교 횟수이다.(tree selection 방법의 경우 tree의 구성에 따라 B(n)과 L(n) 사이이기 때문에 제외.)
표를 보면 항상 B(n) ≤ L(n)임을 알 수 있다.
그럼 원소가 5개 있다고 했을 때 비교횟수는 7개이거나 8개일 것이다. 그럼 여기서 비교횟수가 항상 7개이도록 할 수 있는가?
2-1. 원소가 5개일 때의 정렬
원소가 5개 일 때 무조건 7번 내의 비교를 통해 정렬할 수 있는 방법에 대해서 설명하겠다.
5개의 원소를 K1~K5라고 하자.
우선 merge를 이용한 정렬을 하듯이 비교를 할 것이다.
1.
K1과 K2 비교(+1번)
2.
K3와 K4 비교(+1번)
3.
[K1, K2] 중에서 큰 값과 [K3, K4] 중에서 큰 값 비교(+1번)
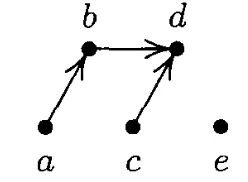
그럼 아래와 같은 그림이 될 것이다.
이제 여기서 a→b→d가 정렬되어있고, 정렬되어 있는 배열에 c와 e를 삽입하면 된다.
이 때, 이진탐색을 이용하여 c와 e를 추가할 것인데 e를 먼저 삽입할 것이다.
e→c인 경우
•
e를 먼저 삽입하는 경우 탐색해야 하는 원소가 a→b→d 3개이므로 최대 비교횟수는 2번이다.(+2번)
•
c를 삽입할 때 탐색해야하는 원소의 개수는 2~3개이다.
1.
e가 d보다 작을 때 ➞ 3개(a, b, e)
2.
e가 d보다 클 때 ➞ 2개(a, b)
•
따라서 e의 위치에 관계없이 c 탐색 시 최대 비교횟수는 항상 2번이다.(+2번)
⇒ 최대 비교횟수: 7번(1 + 1 + 1 + 2 + 2)
c→e인 경우
•
c가 탐색해야 하는 원소의 개수는 2개 이므로 최대 비교횟수는 2번이다.(+2번)
•
e가 탐색해야 하는 원소의 개수는 a~d까지 4개의 원소를 탐색해야 하므로 최대 비교횟수는 3번이다.(+3번)
⇒ 최대 비교횟수: 8번(1 + 1 + 1 + 2 + 3)
이진탐색
n개의 원소가 정렬되어 있을 때 이진탐색을 통해 새로 넣을 원소의 위치를 찾는다고 하면 최대 탐색 횟수는 약 lgn이다.
즉,
- 원소가 1개일 때 ⇒ 탐색횟수 : 1번
- 원소가 2~3개일 때 ⇒ 탐색횟수 : 2번
- 원소가 4~7개일 때 ⇒ 탐색횟수 : 3번
- 원소가 8~15개일 때 ⇒ 탐색횟수 : 4번
이렇듯 이진탐색의 특징을 잘 이용하면 탐색 횟수를 줄일 수 있다는 성질을 이용할 것이다.
2-2. 원소가 더 많을 때의 정렬
위에서 설명했던 방법에서 더 확장해볼 것이다.
21개의 원소가 있고, 현재 위 상태처럼 정렬되어있다고 하자. 우선 앞서 설명한 방식대로 b3까지 삽입할 것이다.
(b3까지 삽입한 후의 모습)
그 후에 다음에 삽입할 원소를 찾아야하는데 c1~c6 6개의 원소(3 * 2)가 정렬되어있고, 이진탐색에서 원소가 4개~7개일 때에는 탐색을 3번만 하면 되므로 a4 1개의 원소(5 - 3 - 1)를 포함하여 7개의 원소(2^3 - 1)에서 탐색하면되는 b5부터 삽입하면된다.
(b5까지 삽입한 후의 모습)
현재 d1~d10까지 10개의 원소가 정렬되어있다. 이진탐색에서 원소가 8개~15개일 때 탐색횟수는 4번으로 같다. 그렇다면 다음에 삽입할 원소는 무엇인가?
바로 b11이다. d1~d10 10개의 원소(5 * 2) + a6~a10 5개의 원소(11 - 5 - 1) = 15개의 원소(2^4 - 1) 안에서 탐색하기 때문에 4번만 탐색하면 되고 그 다음 원소들도 4번만 탐색할 수 있기 때문이다.
이처럼 b1→b3→b2→b5→b4→b11→b10→b9→b8→b7→b6→b21→b20…순으로 삽입해주면 된다.
3. 다음에 탐색해야 하는 원소 찾기
정리하면 처음에는 b1 삽입하고 b3 삽입, 그 후에는 하나씩 내리면서 삽입하되 이미 삽입한 원소에 도달하면 다음에 삽입해야할 원소를 찾고 해당 원소부터 다시 하나씩 내려가면서 삽입하면된다.
우리가 찾아야하는 원소를 t(n)이라고 하겠다.(t1, t2, t3, t4…) = (1, 3, 5, 11…)
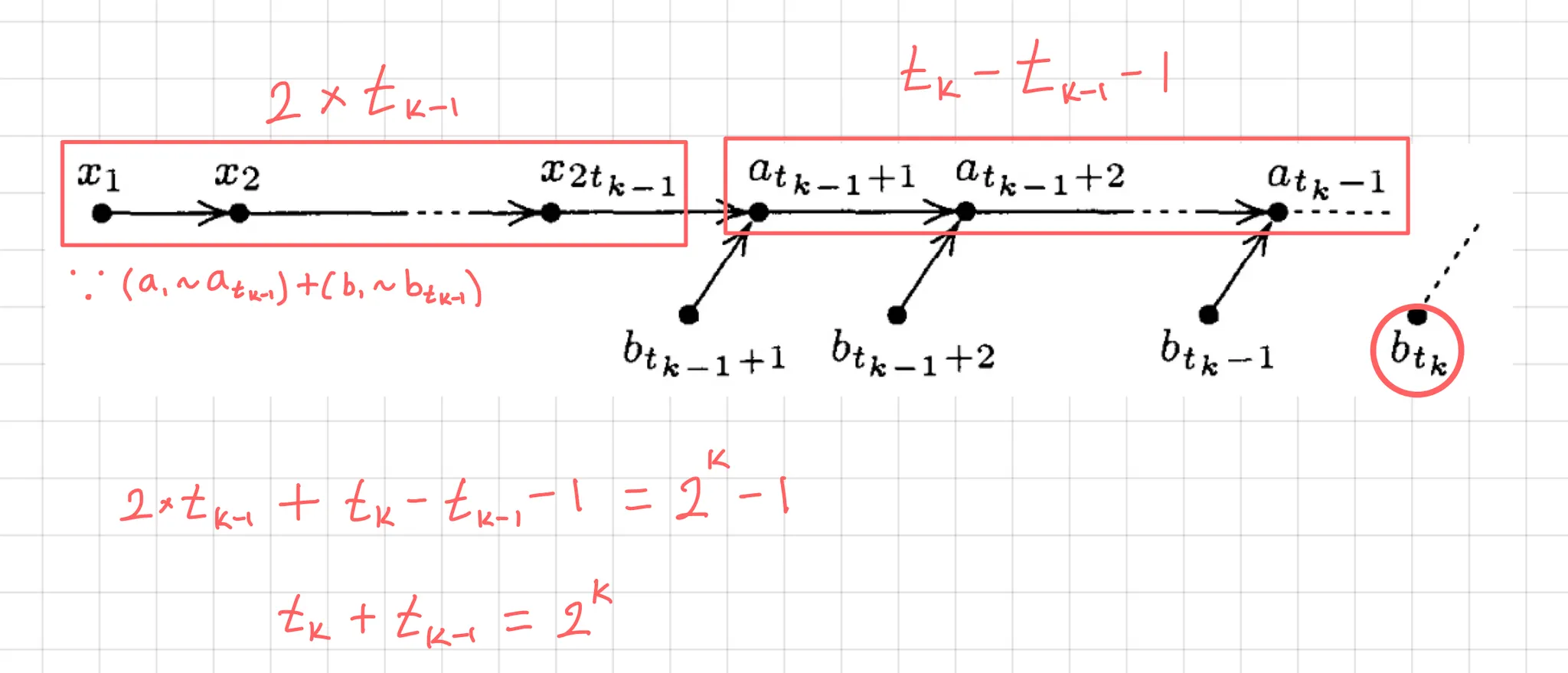
t(n)을 구할 것인데 이미 t(n-1)까지는 b배열의 원소가 삽입되어있고(2*t(n-1)개), A(t(n-1) + 1) ~ A(t(n) - 1)는 b배열의 원소가 삽입되어있지 않다((t(n) - t(n-1) - 1)개). 따라서 (2t(n-1) + t(n) - t(n-1) - 1)개의 원소를 탐색할 것이고, 이 때 원소개수가 2^n - 1 일 때가 t(n)이다.
t(n)값 찾기
2t(n-1) + t(n) - t(n-1) - 1 = 2^n - 1
t(n) + t(n-1) = 2^n이 된다.
그럼 t(n-1) + t(n-2) = 2^(n-1)도 성립할 것이고, 양변에 2를 곱하여
2t(n-1) + 2t(n-2) = 2^n이 된다. 이 식을 위의 식에 대입하면
t(n) + t(n-1) = 2t(n-1) + 2t(n-2)가 되고
t(n) = t(n-1) + 2t(n-2)가 된다.
t(0) = 1
t(1) = 1
t(2) = t(1) + 2t(0) = 1 + 2*1 = 3
t(3) = t(2) + 2t(1) = 3 + 2*1 = 5
t(4) = t(3) + 2t(2) = 5 + 2*3 = 11
t(5) = t(4) + 2t(3) = 11 + 2*5 = 21
…
참고로 이 값들은 jacobsthal number와도 같다.
4. The Ford-Johnson Algorithm 정리
ford-johnson algorithm을 정리해보면 다음과 같다.
1.
정렬해야 하는 배열을 2개씩 짝을지어 pair의 배열로 묶는다.
a.
원소의 개수가 홀수개라면 마지막 원소는 따로 둔다.
2.
서로 짝지어진 원소의 크기를 비교하여 큰 수와 작은 수를 구분한다.
3.
pair 중에서 큰수를 기준으로 pair 배열을 정렬한다.(이 때 pair배열을 정렬할 때에도 재귀를 이용하여 mergeInsertionSort를 통해 정렬하는 것이 이상적이겠지만 타입변환, 스왑 등 여러 문제가…)
4.
정렬된 pair배열에서 큰값과 작은 값을 다른 배열에 담아둔다.
5.
큰값들을 담아둔 배열에 작은 값을 담은 배열의 원소들을 앞에서 구한 방법의 순서대로 하나씩 탐색해서 담는다.(1, 3, 2, 5, 4, 11, 10, 9, 8, 7, 6, 21, 20 …)
6.
원소의 개수가 홀수였을 때 따로 저장해둔 마지막 원소를 이진탐색하여 삽입한다.
끝!
출처
•
The Art of Computer Programming (vol. 3_ Sorting and Searching) (2nd ed.) [Knuth 1998-05-04].pdf
