Search
Duplicate
🧠

[인공지능] 지식을 이용한 추론 - Bayesian Inference & Fuzzy Inference

간단소개
지식을 이용한 추론의 두 가지 개념 소개
팔만코딩경 컨트리뷰터
ContributorNotionAccount
주제 / 분류
A.I
Inference
Scrap
태그
9 more properties

목차

1. 지식을 이용한 추론 A - Bayesian Inference

개요

•
확실히 경계가 그어진 그룹이 있을 때 어떤 지식의 소속 여부가 불확실 할 때 그것을 분류하는 추론
용어 정리

베이즈정리

P(wi∣x)=P(x∣wi)P(wi)P(x)=우도∗사전확률P(x)P(w_i|\mathbf{x}) = \frac{P(\mathbf{x}|w_i)P(w_i)}{P(\mathbf{x})} = \frac{우도 * 사전확률}{P(\mathbf{x})}
•
사후확률 P(wiw_i| x\mathbf{x})
XX 가 주어졌을 때 그것이 부류 wiw_i에서 발생했을 확률 (사후확률)
•
사전확률 P(wiw_i)
사건 발생 이전의 확률 즉, 선택 이전 기반사건의 확률
•
우도함수 P(x\mathbf{x} | wiw_i)
wiw_i 그룹에 x\mathbf{x} 가 속해있을 확률

베이지안 분류기

개요
최소 오류 베이지안 분류기
최소 위험(손실) 베이지안 분류기
식별 함수로 M부류 베이지안 분류기 간소화
식별함수를 이용한 M부류 결정 경계

특성

•
확률분포 모델링의 정확도에 따라 분류 정확도가 좌우된다.
•
실제 데이터와 일치하는 확률분포 값(μ, Σ)(\boldsymbol{\mu,\ \Sigma})을 알 경우 최적의 분류 성능 보장
•
실제로 그것은 불가능하기에 근사치를 이용한 분류가 이루어져 비현실성을 내포

2. 지식을 이용한 추론 B - Fuzzy Inference

개요

•
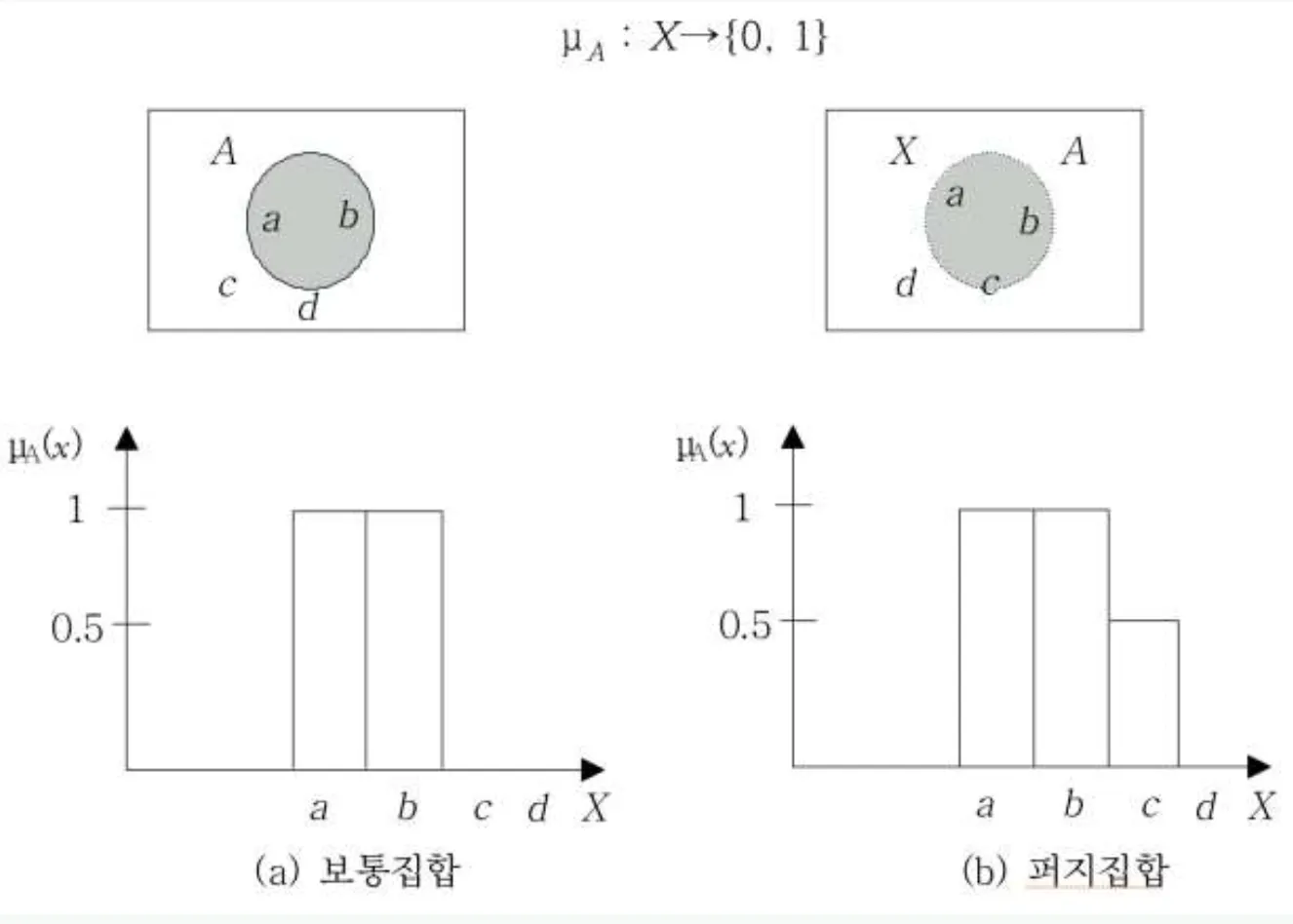
퍼지집합이란?
소속 여부가 확실하지 않은 경우의 집합 - 수학적 집합과 배치(背馳)
Ex) 키 큰 사람의 집합, 맛있는 커피의 집합
•
소속 함수(membership function)
x\mathbf{x}가 집합 AA에 소속될 확률 = μA(x)\mu_A(\mathbf{x})
소속함수는 전체집합 XX 의 모든 원소를 집합 {0, 1}\{0,\ 1\}에 mapping
집합 연산 기초

퍼지 관계

•
집합 X, YX,\ Y사이의 퍼지 관계 RR의 소속함수
μR:X×Y→ [0, 1]\mu_R:X\times Y \rightarrow\ [0,\ 1]
0 이상 1 이하의 어떤 값
X={x1, x2,..., xn}, Y={y1, y2,..., ym} 일 때,X = \{x_1,\ x_2,...,\ x_n\},\ Y=\{y_1,\ y_2,...,\ y_m\}\ 일\ 때,
R=[μR(x1, y1), ⋯μR(x1, ym)⋮⋱⋮μR(xn, y1), ⋯μR(xn, ym)]R=\begin{bmatrix}\mu_R(x_1,\ y_1),\ & \cdots & \mu_R(x_1,\ y_m) \\ \vdots & \ddots & \vdots \\ \mu_R(x_n,\ y_1),\ & \cdots & \mu_R(x_n,\ y_m) \end{bmatrix}
•
퍼지 역관계
μR−1(y,x)=μR(x,y)  for  (y,x)∈Y×X\mu_R^{-1}(y, x)=\mu_R(x, y)\ \ \mathrm{for}\ \ (y, x)\in Y \times X
•
퍼지 합집합 관계
μP∪R(x,y)=max⁡{μP(x,y), μR(x,y)}  for  ∀(x,y)∈X×Y\mu_{P\cup R}(x, y) = \max\{\mu_P(x, y),\ \mu_R(x, y)\}\ \ \mathrm{for}\ \ \boldsymbol\forall(x, y)\in X\times Y
각 엘리먼트 별로 Max 값을 취하면 된다.
•
퍼지 교집합 관계
μP∩R(x,y)=min⁡{μP(x,y), μR(x,y)}  for  ∀(x,y)∈X×Y\mu_{P\cap R}(x, y) = \min\{\mu_P(x, y),\ \mu_R(x, y)\}\ \ \mathrm{for}\ \ \boldsymbol\forall(x, y)\in X\times Y
각 엘리먼트 별로 Min 값을 취하면 된다.
•
퍼지 역집합 관계
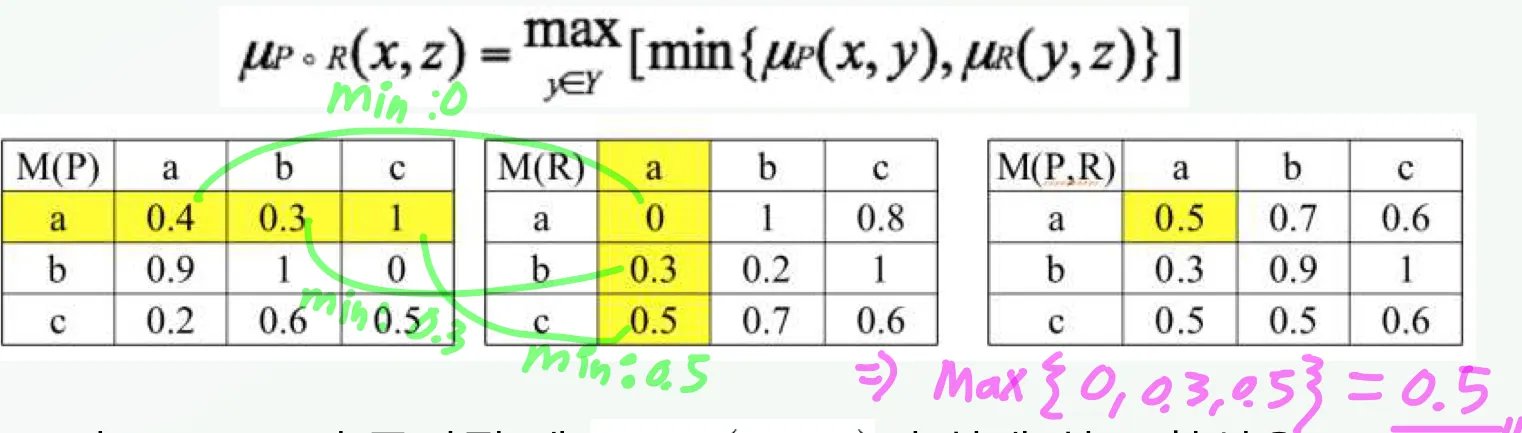
μRc(x,y)=1−μR(x,y)  for  ∀(x,y)∈X×Y\mu_{R^c}(x, y) = 1-\mu_{R}(x, y)\ \ \mathrm{for}\ \ \boldsymbol{\forall}(x,y)\in X \times Y
•
퍼지 관계의 합성
추론 교칙의 합성법: 대응하는 각 셀의 최소값을 구한 후 이들의 최대값을 선택

퍼지 논리

•
퍼지 논리식 f
논리식의 값이 구간 [0,1][0, 1]사이의 값을 가질 수 있도록 확장
f:[0,1]n→[0,1]\mathrm f :[0,1]^n \rightarrow [0,1]
•
퍼지 논리식의 연산자
◦
부정 (negation)
aˉ=1−a\bar{\mathrm{a}} = 1 - \mathrm{a}
◦
논리곱 (conjunction)
a∧b=min⁡(a,b)\mathrm{a}\land\mathrm{b} = \min(\mathrm{a},\mathrm{b})
◦
논리합 (disjunction)
a∨b=max⁡(a,b)\mathrm{a}\lor\mathrm{b} = \max(\mathrm{a},\mathrm{b})
◦
조건명제 (implication)
a⇒b=min⁡(1, 1−a+b)\mathrm{a}\Rightarrow\mathrm{b} = \min(1,\ 1-\mathrm{a}+\mathrm{b})
•
퍼지 술어
술어에서 객체의 성질을 나타내는 술어가 퍼지집합일 때 퍼지술어(fuzzy prediction)으로 정의됨

퍼지 이론 응용 분야

•
인공지능, 지능 제어, 전문가 시스템, 패턴 인식
•
의료, 정보 검색, 가전제품
•
의사 결정 지원, 앙케이트 조사

Human annotation

•
Human annotation을 사용 할 때 학습의 기준이 되는 진리표가 필요하다.
이 진리표는 복수의 사람이 실제 데이터를 분석한 것을 이용하여 만들어진다.
•
이러한 진리표를 만드는데 몇가지 장애 요인이 있다.
◦
사람의 감정의 스펙트럼이 넓고, 같은 자극에도 개인간 편차가 존재한다.
→ variance between persons
◦
더욱이 같은 사람이라도 당시의 컨디션 등 통제할 수 없는 외부 요인에 의해 판정이 달라질 수 있다.
→ variance within a person
Made with