백트래킹 이란?
백트래킹(BackTracking) 알고리즘이란 퇴각검색이라고도 불리며 이는 한정 조건을 가진 문제를 풀려는 전략이다. 쉽게 설명해서 어떤 문제를 푸는데 있어 모든 경우의 수를 시도하여 문제의 정답을 찾아나간다. 하지만 백트래킹에서는 한정 조건 에서의 모든 경우의 수를 시도하는 것이기 때문에 실제로 상당한 경우의 수들이 배제되기 때문에 단순 다중 for문 보다는 빠르게 해결되는 경우가 많다.
구현은 어떻게 할까?
보통 백트래킹(BackTracking)의 구현은 BFS나 DFS와 함께 구현한다. 모든 경우의 수에서 한정 조건을 만족하는경우를 탐색하는 것이기 때문에 완전탐색기법인 BFS와 DFS가 모두 구현이 가능하다. 하지만 백트래킹의 특성에서 한정 조건에 부합하지 않다면(Node가 유망하지 않다면) 이전 수행(이전 Node)으로 돌아와야하기 때문에 BFS보다는 DFS의 구현이 더 편하다. 구현할 때 가장 중요한 것이 한정 조건 이다. 한정 조건을 걸어 완전탐색에서 유망하지 않은 시도를 걸러내는 것이 바로 백트래킹의 본질이다. 그럼 한정 조건이 정확히 무엇인지 어떤식으로 작동하지는 예제를 통해서 알아보도록 하자.
백트래킹의 Key : 한정 조건
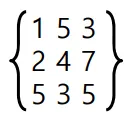
먼저 3X3 행렬 선택 게임은 아래와 같은 행렬이 존재할 때 3개의 숫자를 선택하는 게임이다. 단, 선택한 숫자들의 행과 열은 모두 중복하면 안된다. 가장 적은 점수를 얻는 것이 승리하는 것이라 할때 선택해야하는 숫자 3개를 골라보자.
먼저 이 문제를 푸는 가장 쉬운 방법은 당연히 모든 방법을 다 해보는 것이다. 숫자 3개를 선택하는 모든 경우를 다해보는 것이 정답이지만 이 문제에서는 조건이 하나 있다. 고른 숫자는 모두 행과열이 달라야 한다는 것이다. 이것이 바로 전에 설명했던 한정 조건 이다. 이 문제에서의 한정 조건은 '행과열이 달라야 한다.' 인 것이다. 먼저 이 문제를 구조화 한다면 아래와 같이 나타낼 수 있다.
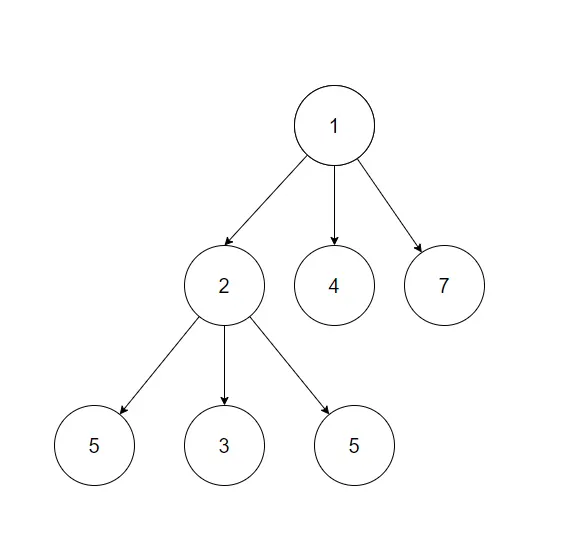
3X3 행렬을 트리 구조로 구조화 한 모습
위 구조화 그림은 한정 조건과 상관없이 모든 경우의 수를 나타낸 구조이다. 만약 여기서 한정 조건을 추가한다면 아래와 같은 구조가 될 것이다.
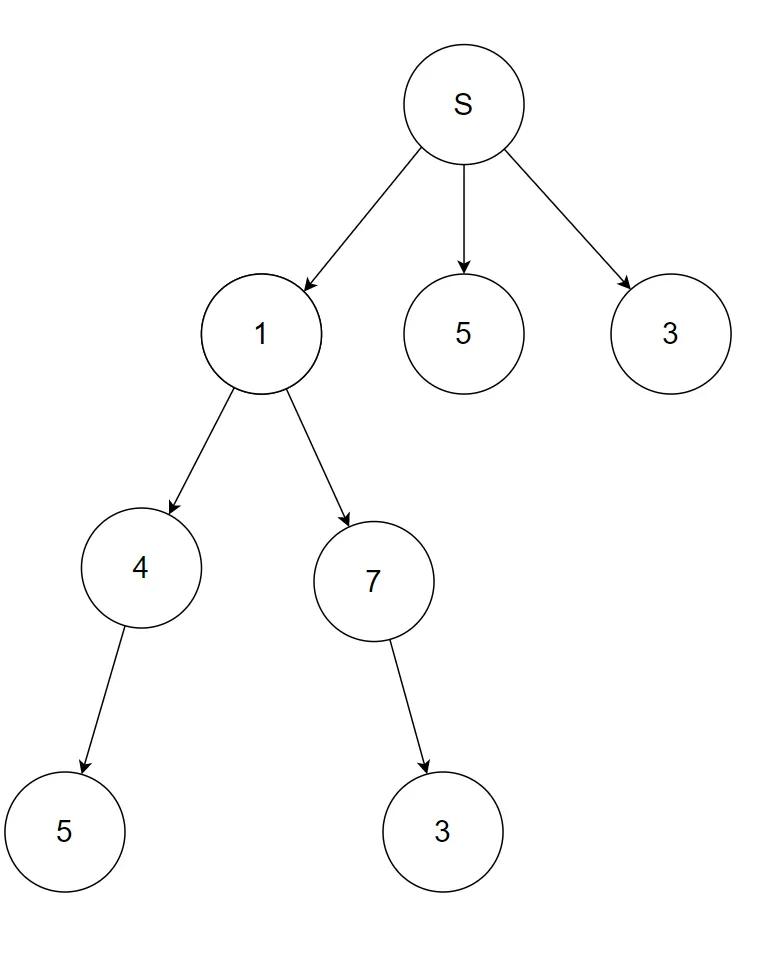
3X3 행렬 트리 구조를 한정 조건을 적용하여 나타낸 모습
차이점이 한눈에 보이는 것을 알 수 있다. 위와 같이 한정 조건 을 적용한 뒤에 DFS 를 통해서 전체 탐색을 진행하는 것이 바로 백트래킹이다. 예제로 설명하자면 첫번째 행에서 만약 1을 택한다면 두번째 행의 숫자는 2,4,7이 존재하지만 2는 1과 같은 열이기 때문에 더 탐색하더라도 정답이 될 수 없다. 따라서 첫번째를 1을 선택하면 2는 유망하지않고 4와 7만 유망하기 때문에 4와 7만을 Node에 추가시킨다. 이러한 방식으로 가장 마지막 행까지 모두 수행하면 위와 같은 트리 구조를 얻을 수 있고 결론적으로 정답을 찾을 수 있는 것이다. 추가로 DFS는 아래와 같은 과정으로 탐색하는 것이다.
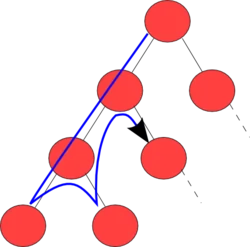
DFS 기본 탐색 구조
따라서 백트래킹은 위와 같이 한정 조건 을 통해서 탐색할 Node가 유망한지 판별하고 유망한 Node만을 추가하여 탐색하는 기법이라고 할 수 있다.
실제 코드로써의 구현
import sys
li = [[1,5,3],[2,5,7],[5,3,5]]
chk = [False]*3
m = sys.maxsize
def backtracking(row, score):
if row == 4: # 재귀함수를 마치는 조건
if score < m:
return
for i in range(1,4):
if chk[i] == false: # 백트래킹에서의 한정조건
chk[i] = true
backtracking(row+1, score + li[row][i])
chk[i] = false
return
backtracking(1,0)
print(m)
Python
복사