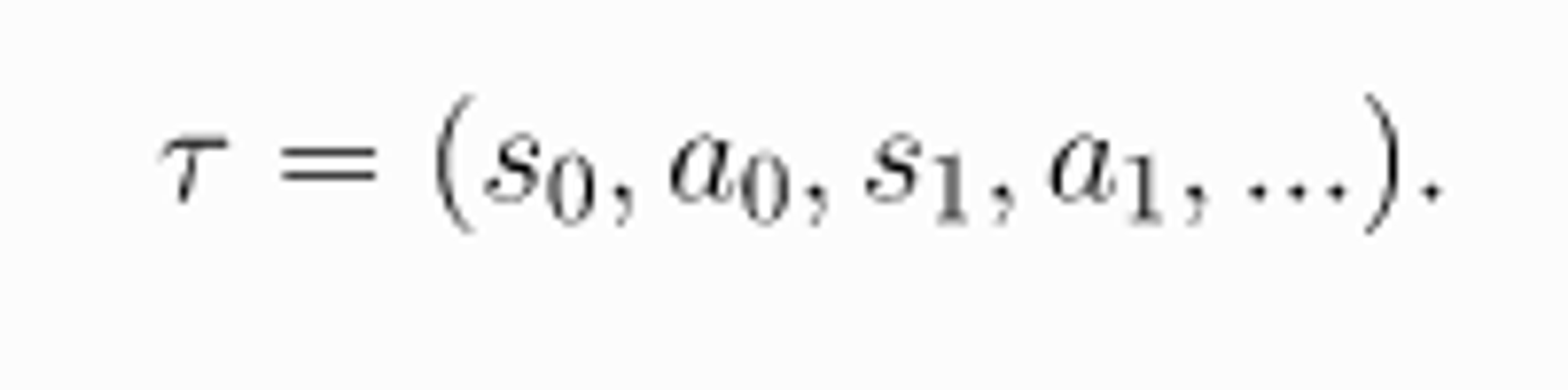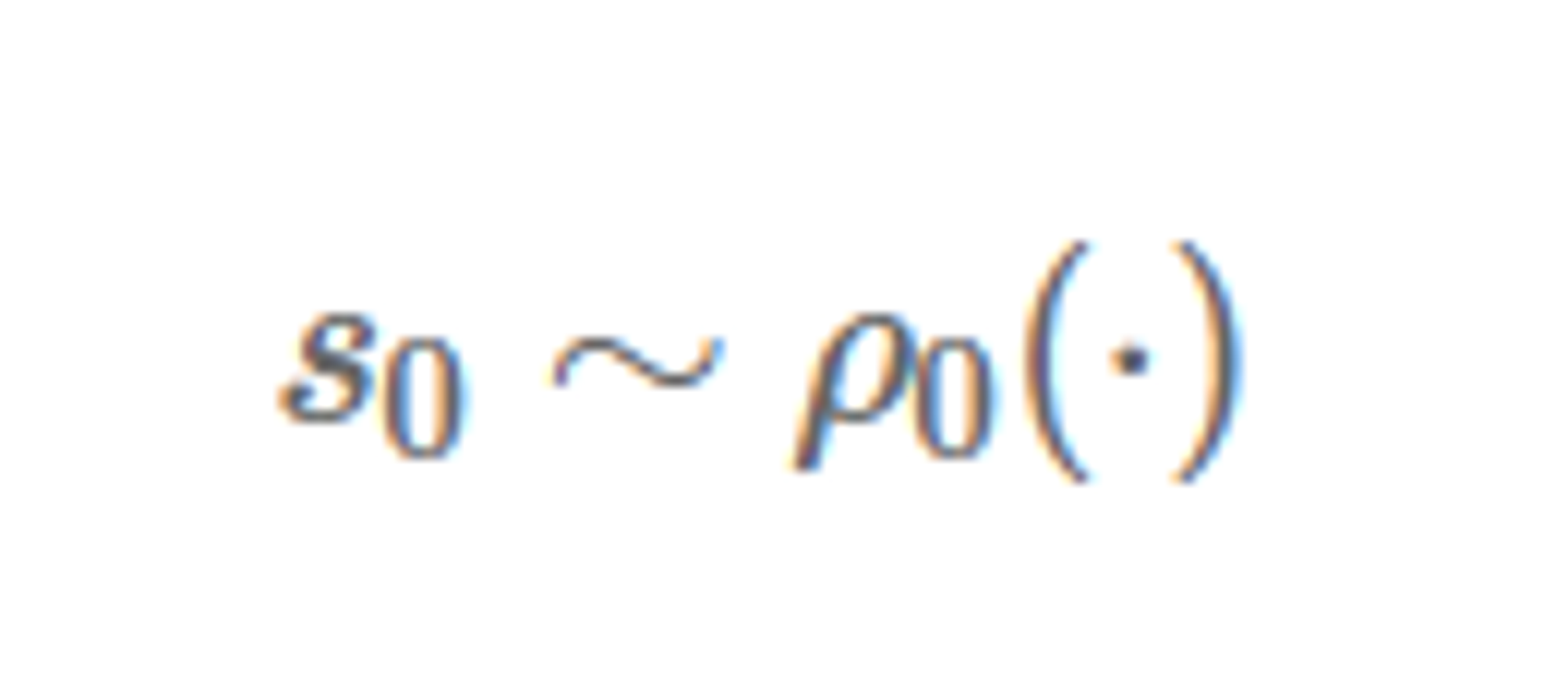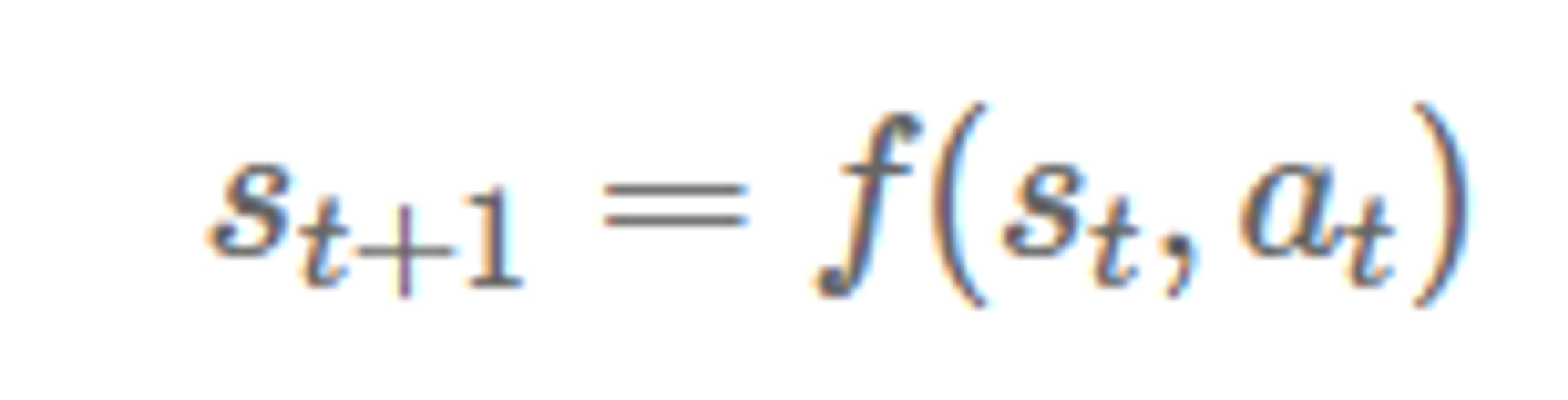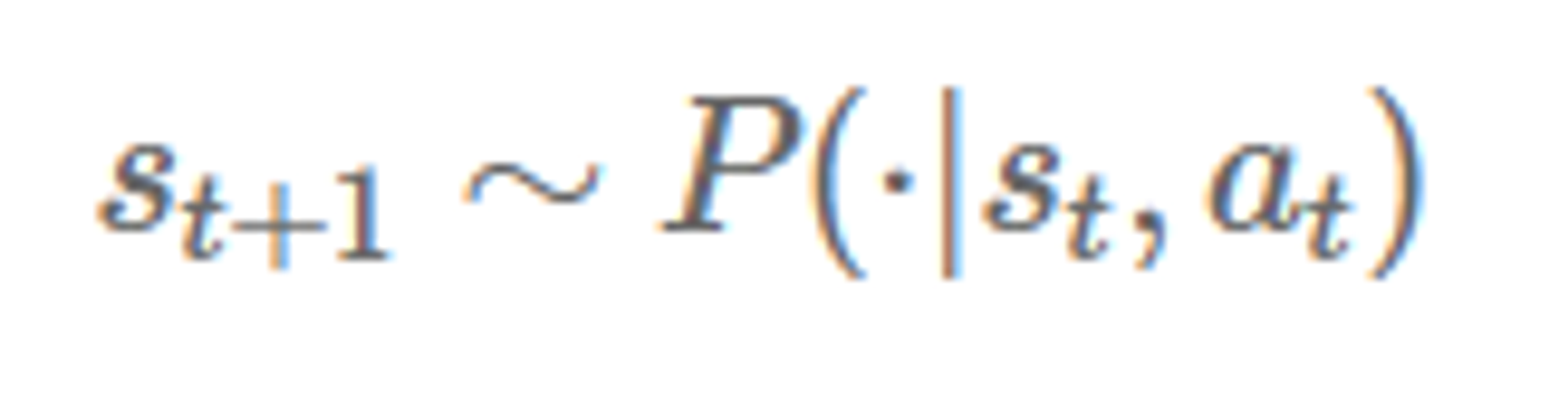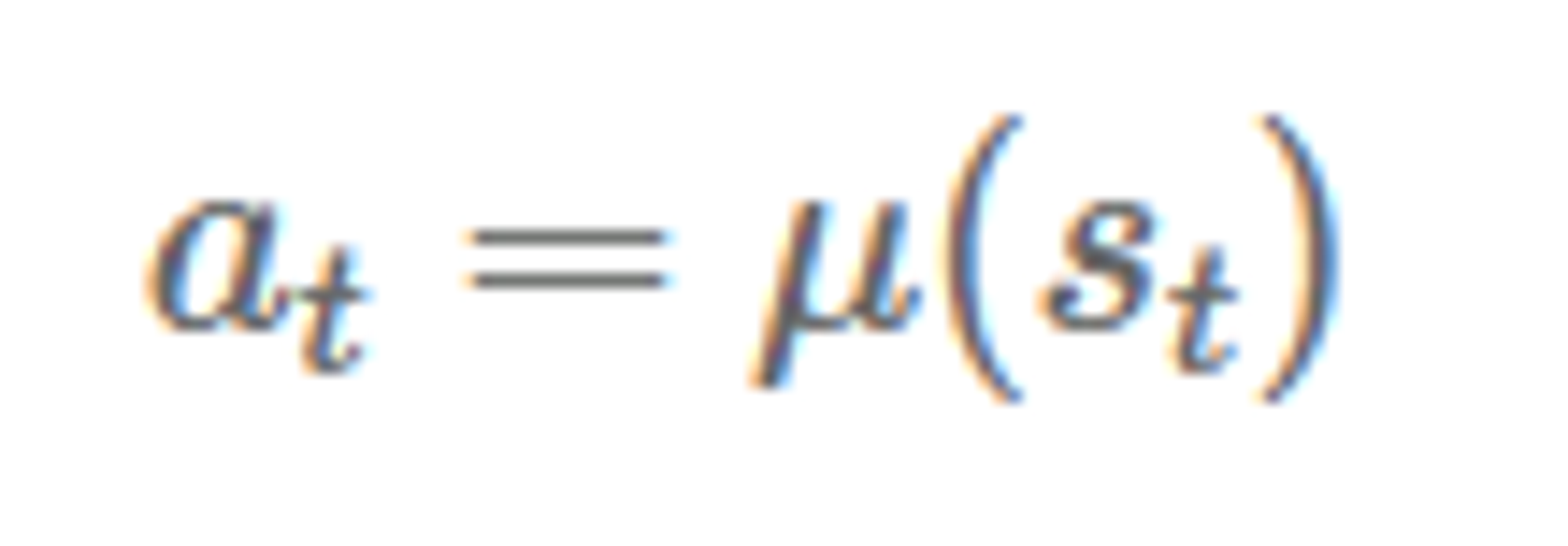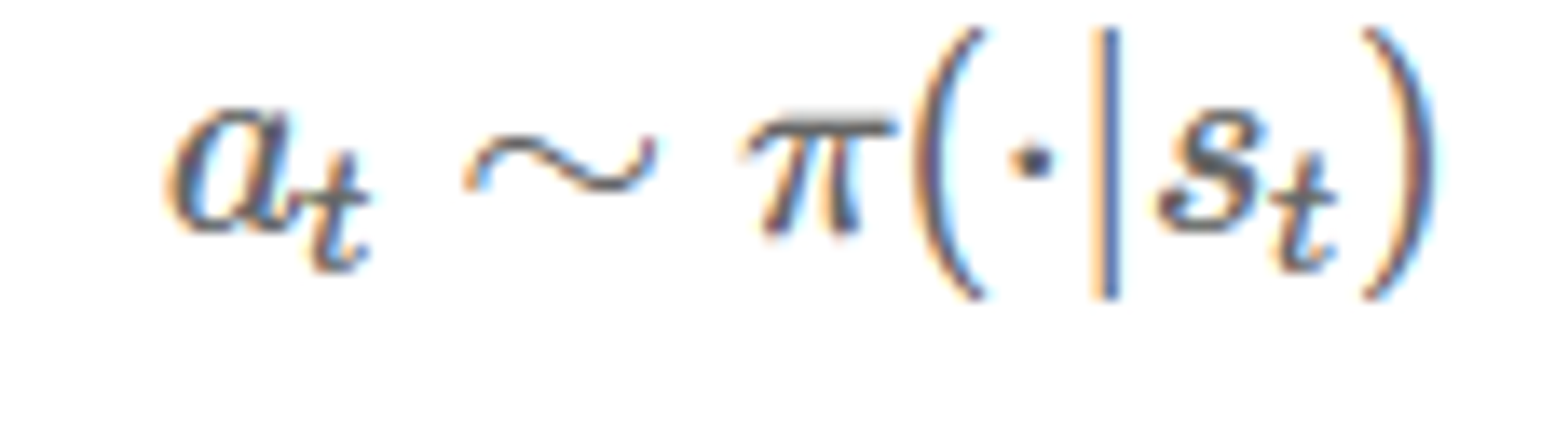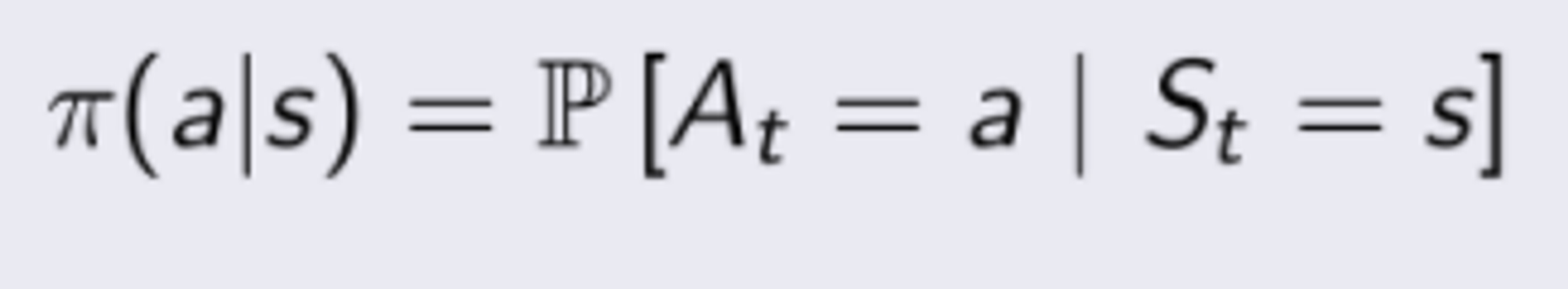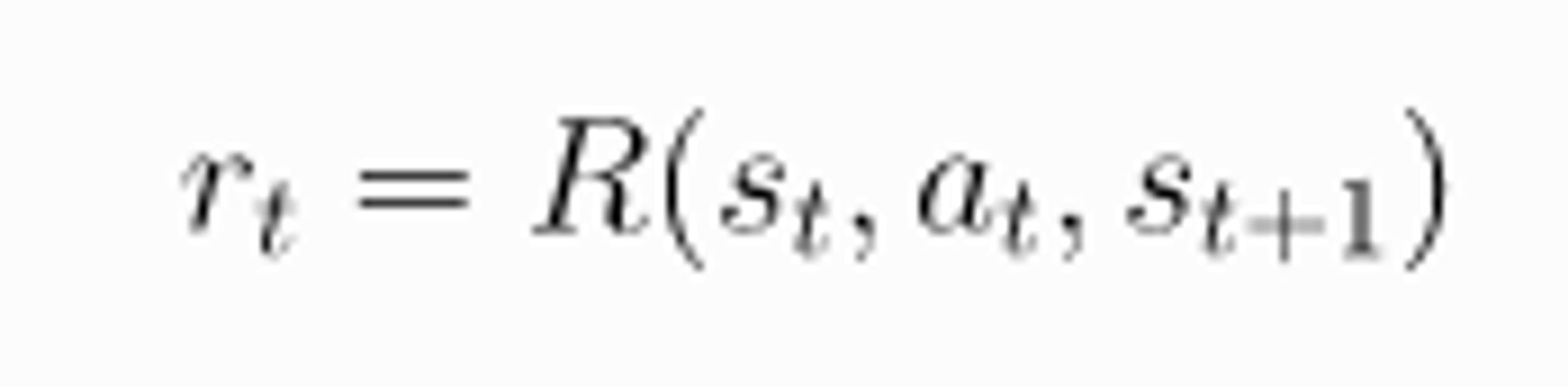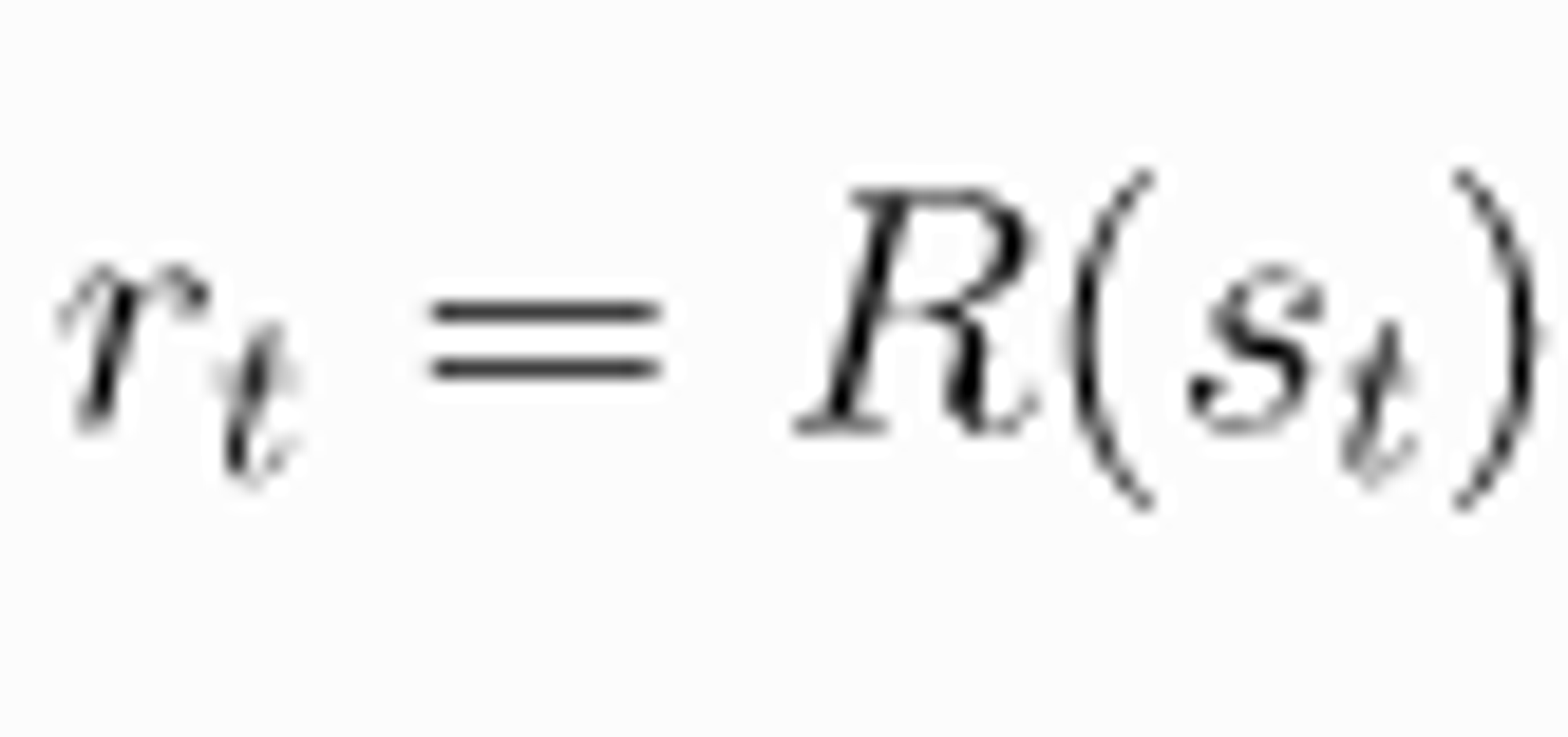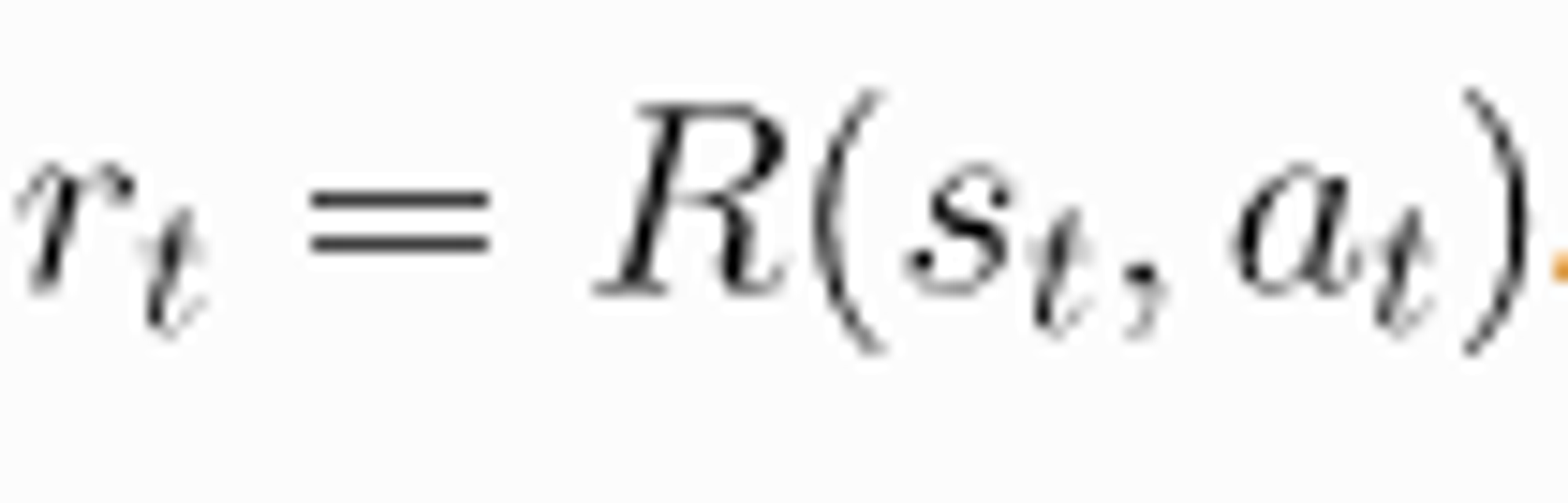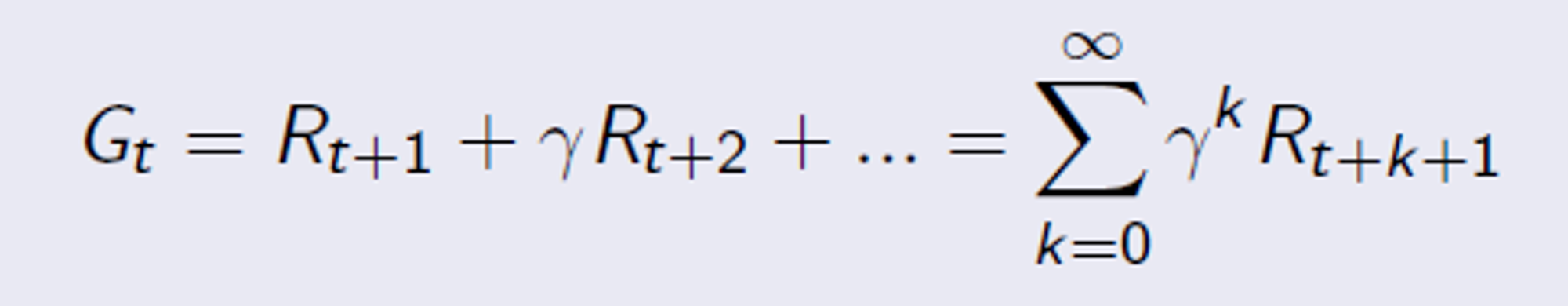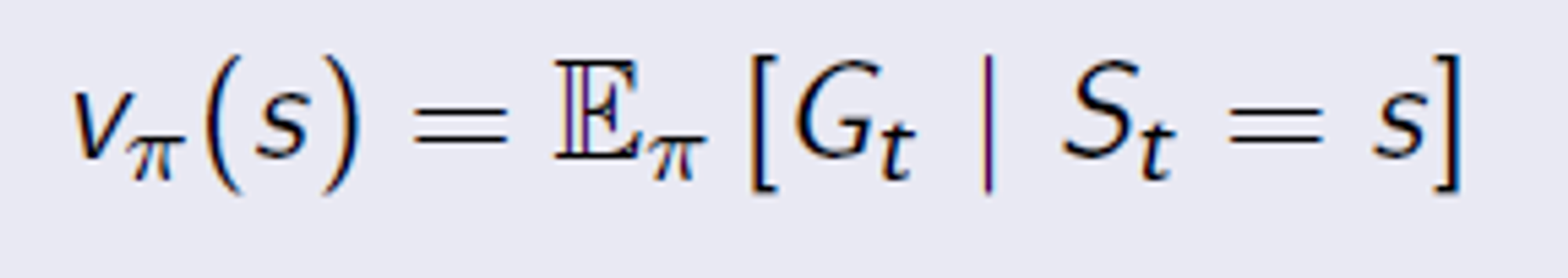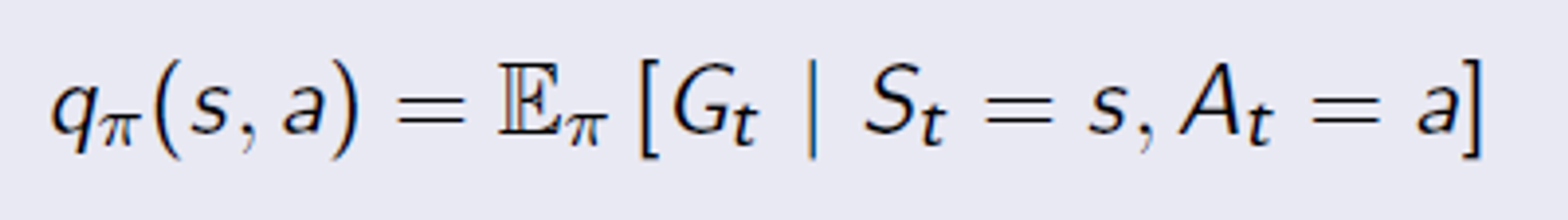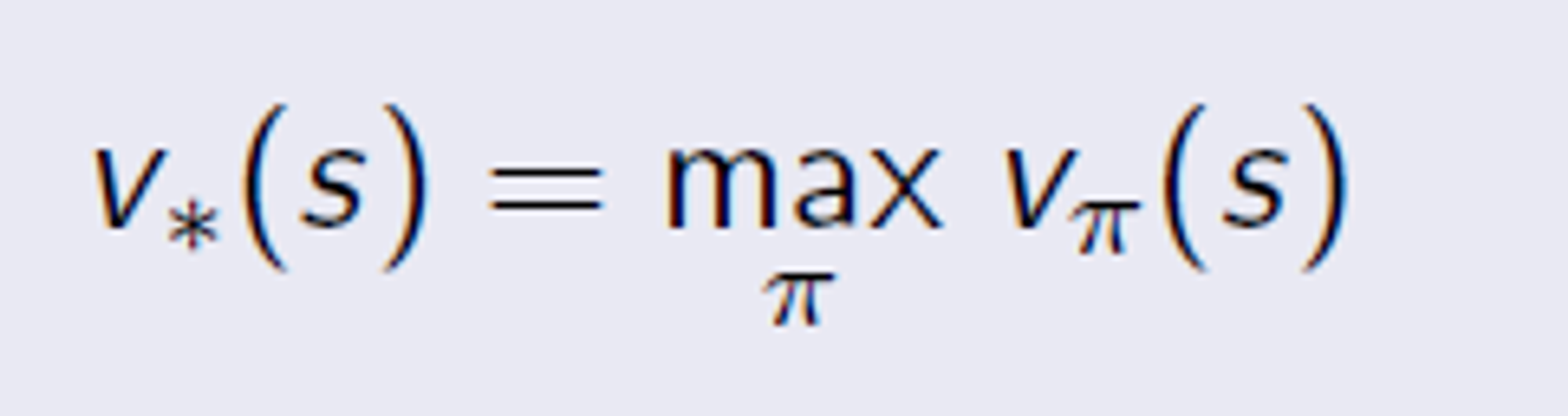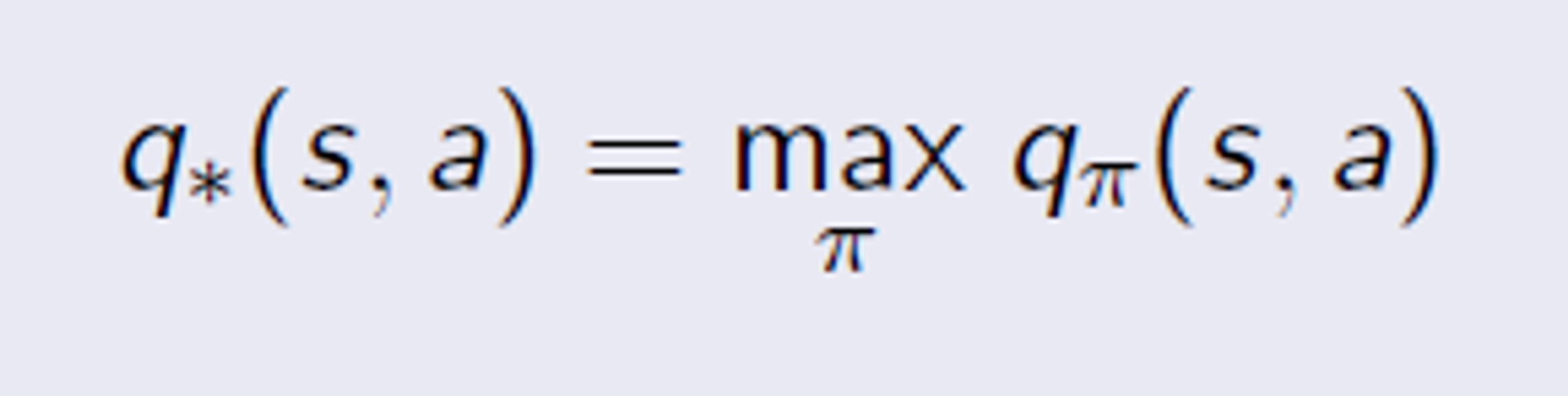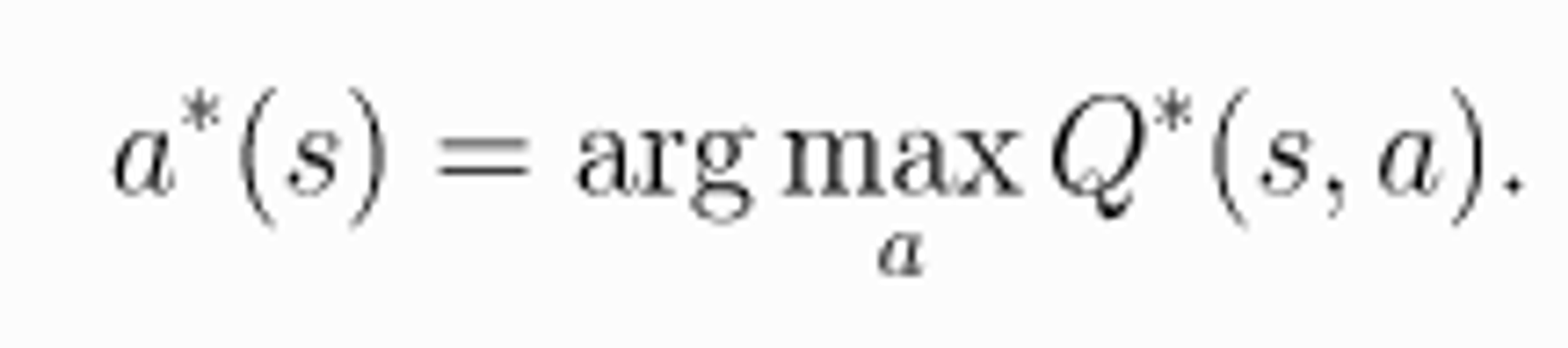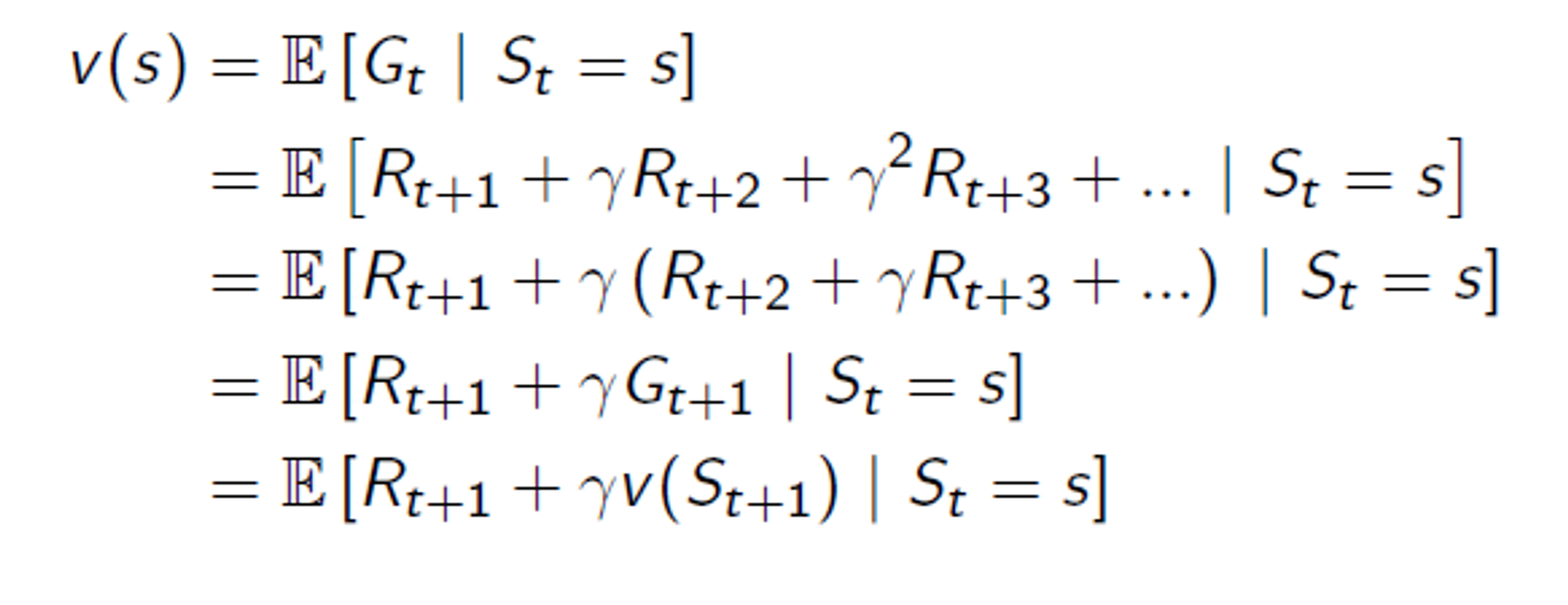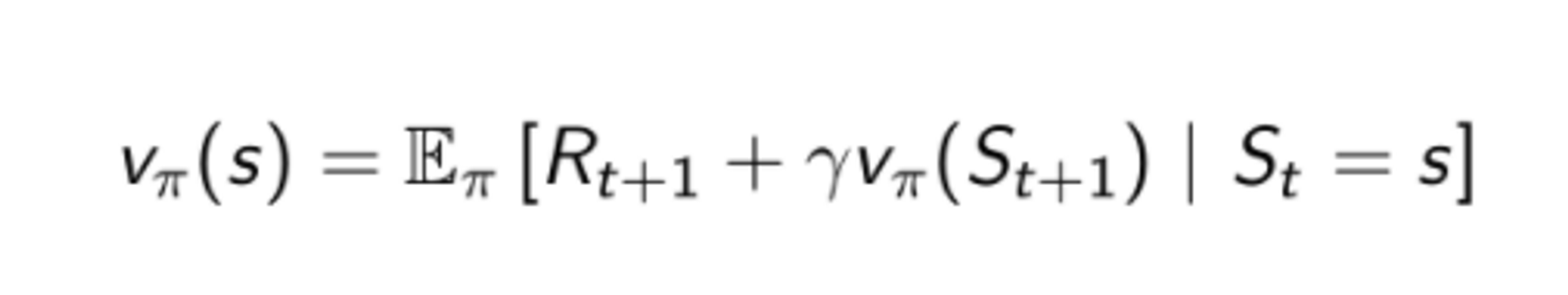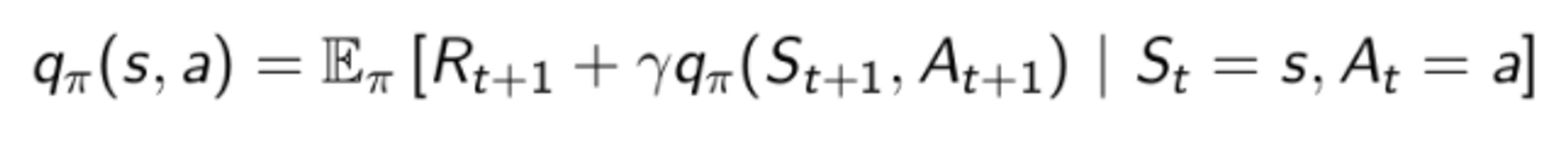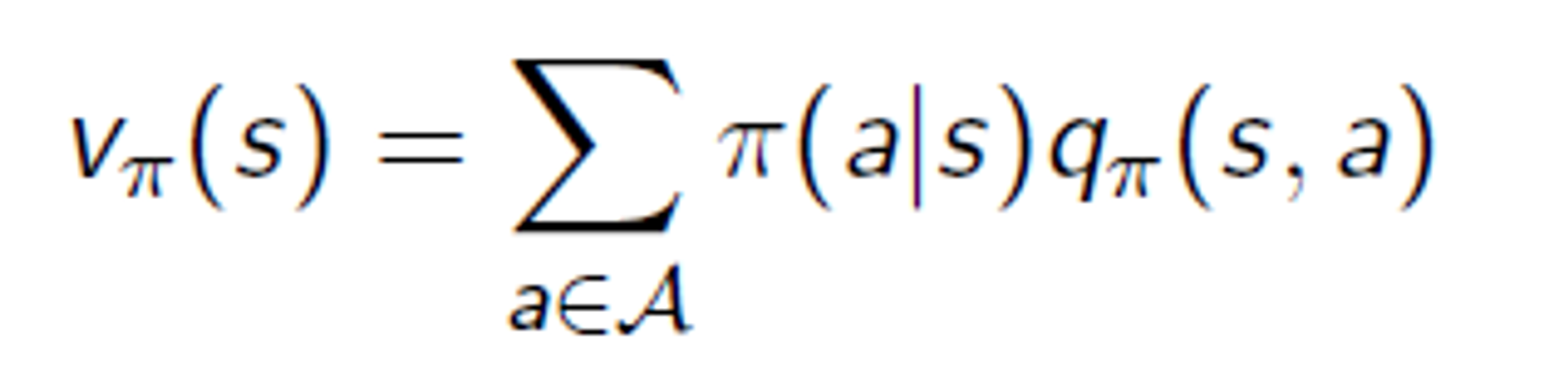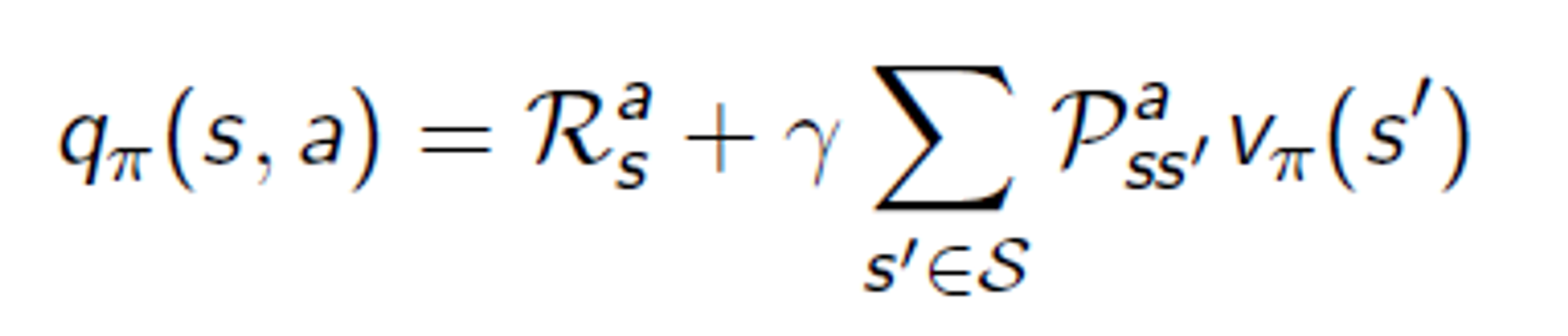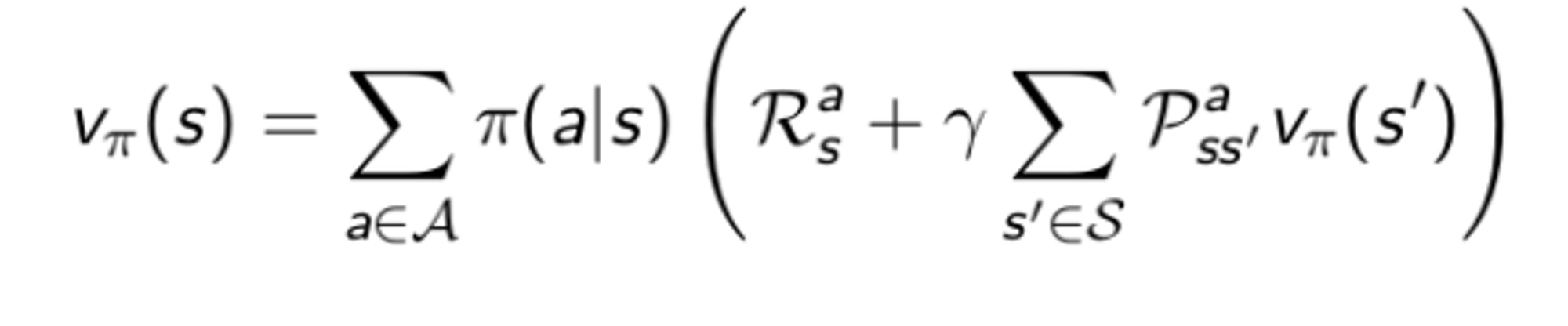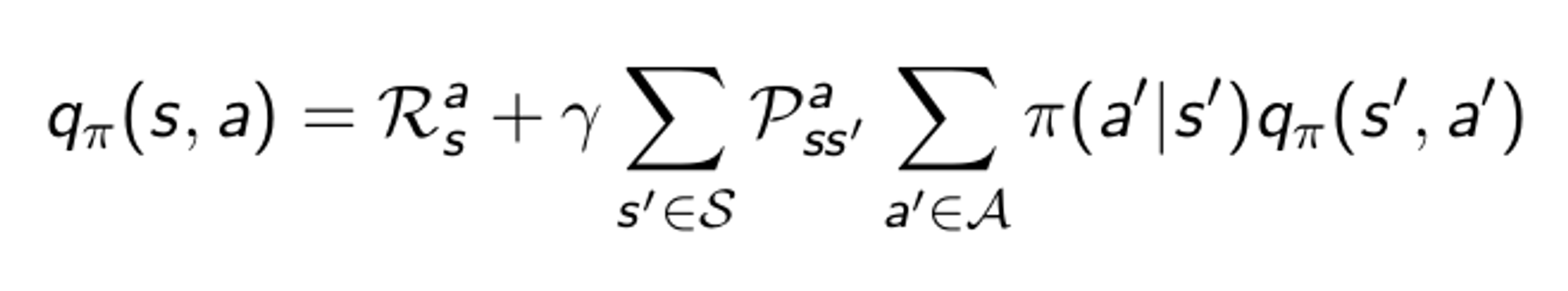강화학습이란?
강화 학습(Reinforcement learning)은 기계 학습의 한 영역이다. 행동심리학에서 영감을 받았으며, 어떤 환경 안에서 정의된 에이전트가 현재의 상태를 인식하여, 선택 가능한 행동들 중 보상을 최대화하는 행동 혹은 행동 순서를 선택하는 방법이다. - 위키피디아
정의는 이렇게 나와있는데 뭔가 정의내리기 참 힘든 것 같다. 나중에 내가 안 헷갈리게 좀 더 자주나오는 용어나 개념들을 정리를 해보자.
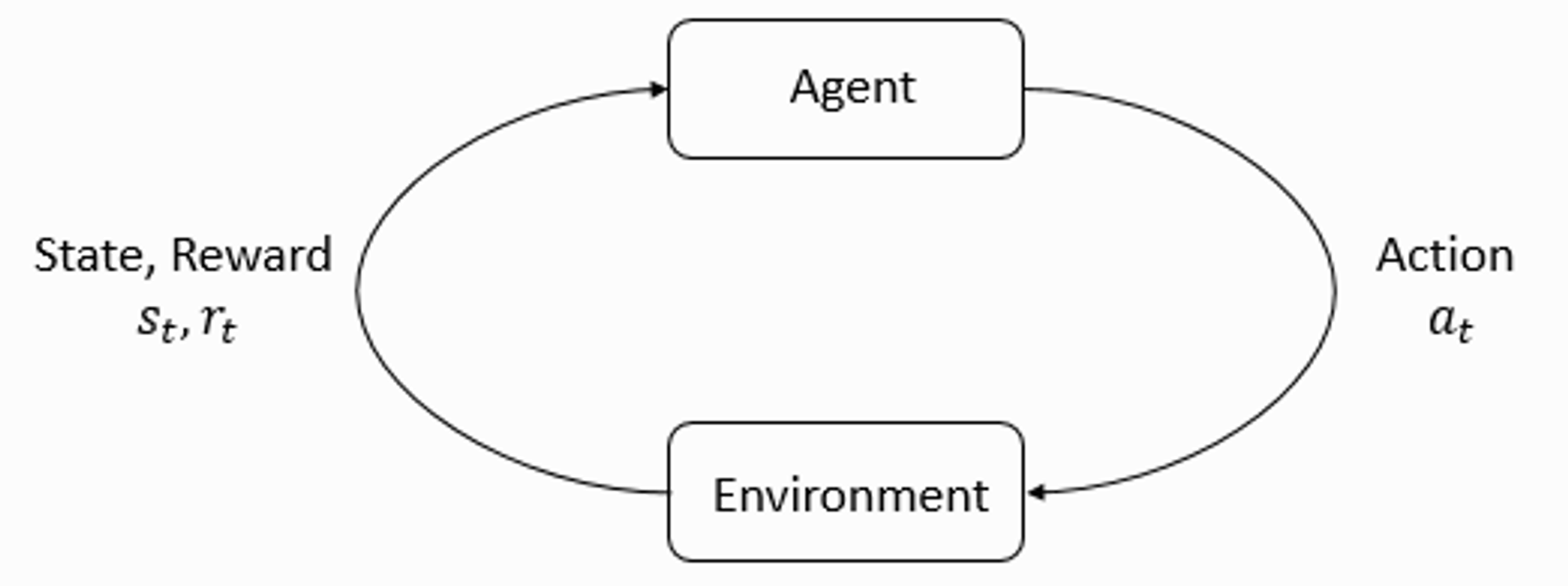
위 그림은 강화학습의 가장 기본인 에이전트와 환경간의 상호작용을 표현하였다.
Environment(환경)은 에이전트에게 State(상태)와 Reward(보상) 정보를 준다. 에이전트는 그것들을 관찰하고 가지고 있는 Policy(정책)에 따라서 Action(행동)을 내린다.
이게 대략적인 그림이고 이제 좀 더 들어가서 살펴보자.
Agent
강화학습에서 의사결정을 하는 역할. 여럿이 있으면 multi-agent 이다.
Environment
에이전트의 의사 결정을 반영하고 에이전트에게 정보를 주는 시스템. 게임 그 자체
State 와 Observations
State s 는 환경에서의 상태를 표현한 것을 말한다. 반면 Observation o 는 State 를 부분적으로 표현한 것으로 일부 정보가 누락 되어 있을 수 있다. Agent 가 환경의 모든 state 를 관찰할 수 있으면 해당 환경을 fully observed 라고 하고 일부분만 볼 수 있으면 partially observed 라고 한다.
시간 t 를 붙여서 St Ot 로 표기한다.
Action
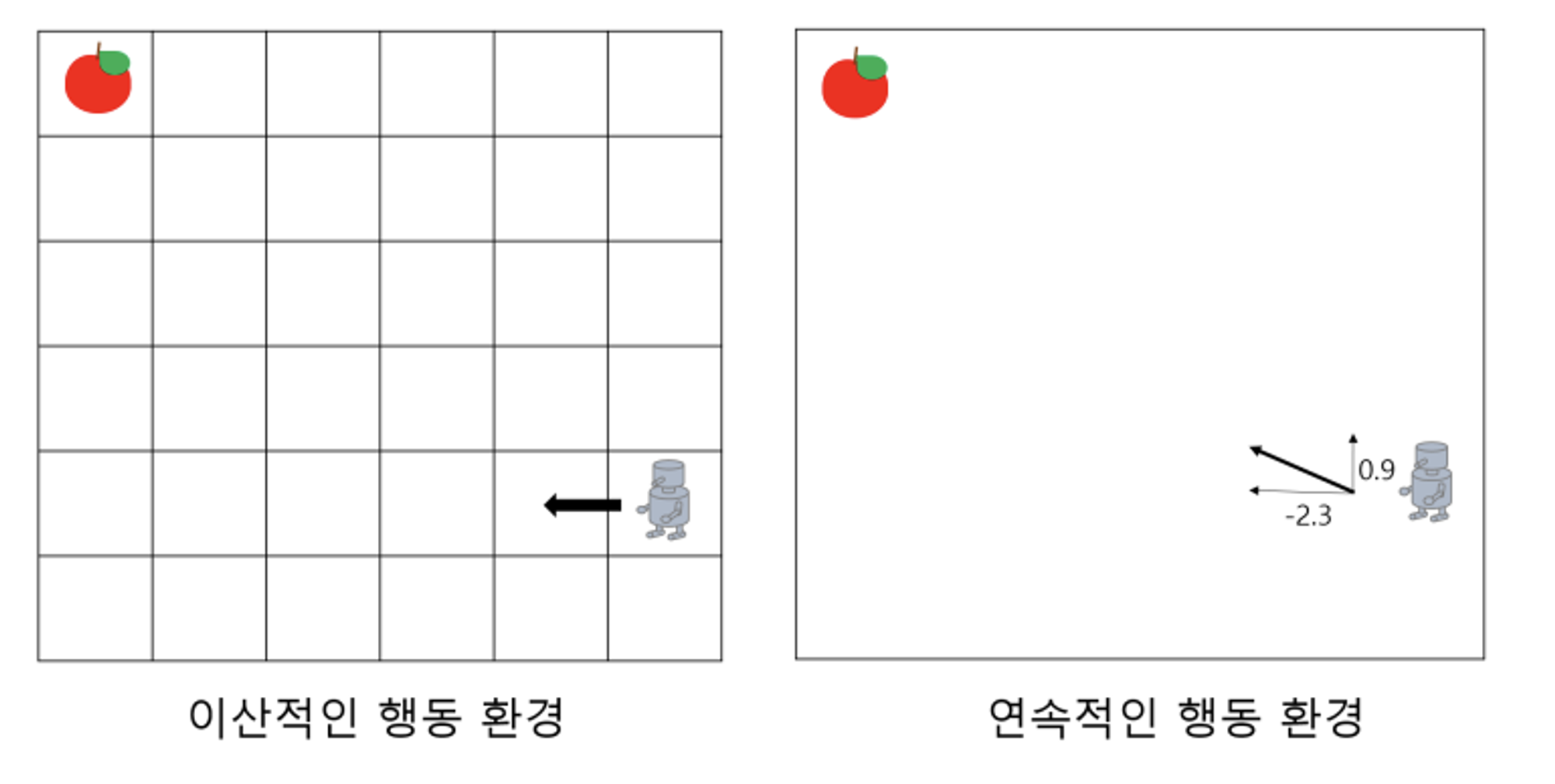
Agent 가 의사 결정을 통해 취할 수 있는 행동이다. 이 때 모든 가능한 action 의 집합을 Action space 라고 한다. Action 이 이산적이면(discrete) Action space 도 discrete action space 일거고 Action 이 연속적이면(continuous) continuous action space 일 것이다.
시간 t 를 붙여서 At 로 표기한다.
Step & Episode(Trajectory, or Rollouts)
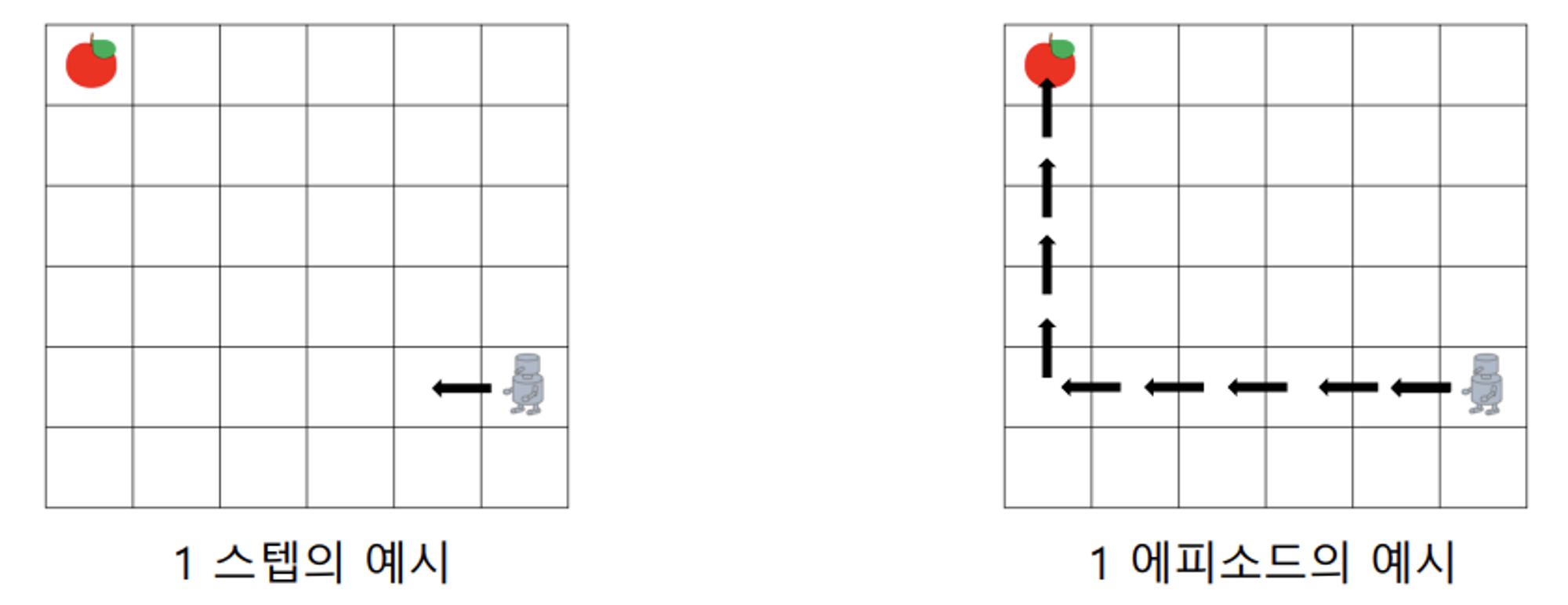
Step : Agent가 한번 행동을 취하는 것
Episode(Trajectory): trajectory τ 은 환경에서 state 와 action 의 sequence 형태를 말하며 다음과 같이 표현한다.
게임 한 판 이라고 보면 된다.
Start-state distribution
Agent 가 가질 수 있는 처음 상태 s0 들을 모아놓은 것이다.
State transition(state transition function, transition probability function)
상태 St 에서 행동 At 를 했을 때 다음 상태 St+1 이 될 확률이다. 상태의 변화는 바로 전 상태 St 와 가장 최근 행동 At 에 의해서만 영향을 받는다! 식으로 써보면
만약 deterministic 하면
만약 stochastic 하면
이렇다.
이렇게도 표현되므로 여러 표현들을 기억해두자.
Policies
Policy(정책)은 agent 가 어떤 행동을 할지 결정하기 위해 사용하는 규칙이다.
만약 policy 가 deterministic 하면
만약 policy 가 stochastic 하면
이렇게 표기 할 수 있다.
보통 policy 는 stochastic 하고 그래서 다르게 표현하자면 Policy 는 특정 상태가 주어졌을 때 어떤 행동을 할 확률 분포이다.
"Agent" 라는 단어를 "Policy" 라고 대체해서 쓰기도 한다. 나중에 이 policy 를 parameterized 해서 특정한 parameter 들을 넘겨서 조절할 수 있다는데 이 부분은 좀 더 봐야겠다.
Reward & Return & Value Function & Discount Factor 등등
Reward 관련된 부분이 매우 중요하다. 그리고 매우 어렵다. 다 이해는 못하겠지만 일단 적어보자. 추후 각각의 강화학습 알고리즘을 공부하고 나면 좀 더 이해가 될 것 같다.
먼저 Reward 가 먼지 알아보자.
Reward 는 어떤 state 에서 agent 가 어떤 행동을 했을 때 환경이 주는 신호이다. 이 것을 수식으로 표현 해보면
이렇게 표현 할 수 있다. Reward Function R 에 입력값으로 St, At, St+1 이 들어가는 데 더 간단히 하여서
로 표현 하기도 한다.
환경이 주는 보상을 당장 다음 행동까지만 보는 게 아니라 먼 미래까지 끝까지 봐야한다. 그런데 지금 당장 밥 먹는게 내일 밥 먹는거보다 더 좋듯이 미래의 보상은 좀 깎아서 생각해야 한다. 여기서 Discount Factor(감가율) 이 나온다. Discount Factor(감가율) 을 0~1 사이의 값으로 잡아서 미래에 얻을 수 있는 보상에 곱해주어서 미래의 얻는 보상을 적절히 줄인다.
다음은 Return 이다.
Return Gt 는 시간 t 부터 discount factor(감가율) 를 고려해서 향후 모든 reward 의 총합이다. 이를 식으로 표현해보면
요렇게 쓸 수 있다.
이제 엄청나게 중요한 Value Function(가치 함수) 에 대해서 알아보자.
Value Function(가치 함수)는 특정 state 또는 (state, action) 쌍의 value 를 나타내는 함수이다. 이 value 를 계산할 때 바로 위의 Return 이 이용된다. 현재 state 이나 (state, action) 쌍으로부터 앞으로 받을 수 있는 Return 의 기대값이 바로 value function 이다. 앞으로 할 action 들은 policy 에 의해서 결정되므로 policy π 에 대한 기호도 식에 들어가게 되는데 한번 식을 보자.
State Value Function
이 식은 Policy π 를 적용했을 때 특정 state 의 가치를 나타내는 Value Function 이다. 이렇게 특정 state 만 들어가면 State Value Function 이라 부른다.
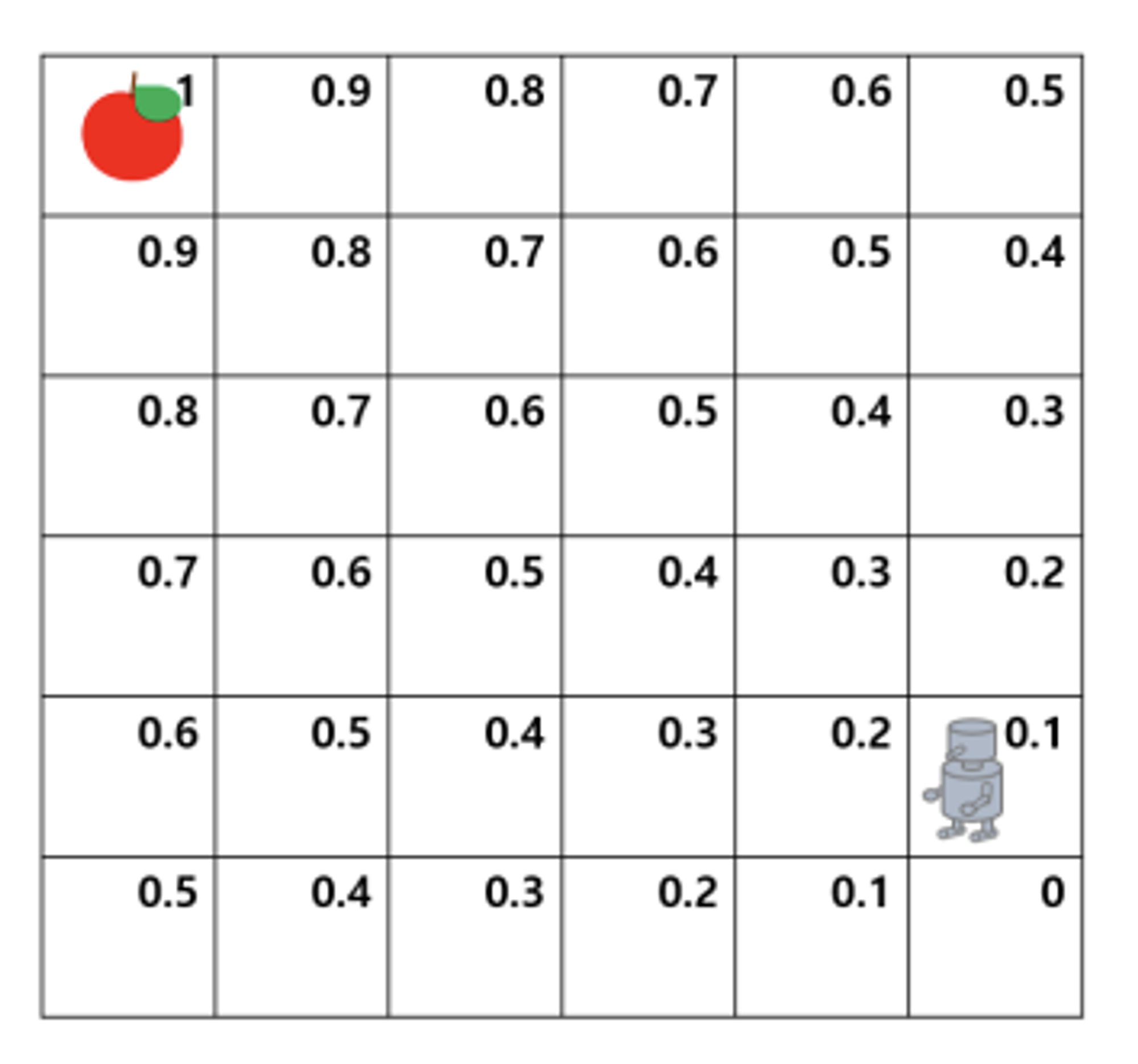
이런 느낌
Action Value Function
Action value function, 또는 Q Function, Q value 라고 부른다. 특히 Q function 이라고 하고 앞으로 매우매우 많이 나올 용어이니 반드시 기억해야한다. 식을 보면 상태와 행동에 대해서 return 의 기대값을 나타낸다.
이런 느낌
그런데 어떤 정책을 쓰느냐에 따라 이 값들이 다 달라질 수 있다. 그래서 뭔지는 모르겠지만 가장 좋은 정책을 사용했다고 생각하면 이제 optimal 을 앞에 붙일 수 있다. 다음 식들을 보자.
Optimal State Vaule Function
Optimal Action Value Function
각각 value function 중 제일 좋은 policy 를 고른거다.
Optimal action value function 에서 최적의 행동을 표현한 식 하나만 더 보고 넘어가자.
이제 진짜 거의 다 왔다. 마지막으로 Bellman Equation 으로 넘어가자.
Bellman Equation
벨만 방정식은 현재 state 의 value function 과 다음 state 의 value function 사이의 관계식이다.
다음 그림을 보고 value function을 현재 와 다음 state 로 분리하는 것을 보자.
위 그림처럼 state value function 을 현재 reward 와 다음 상태의 value 에 discount factor 를 곱한 것으로 나눌 수 있다.
이제 여기에 policy 만 넣어주면 된다.
Bellman equation for state value function
Bellman equation for action value function
이렇다...
그런데... 이거를 다른 식으로 표현해야 한다고 어디서 배웠다... 설명은 조금 생략하고 다른 식으로 표현하는 법을 보면
이렇게 쓸 수 있고 이 두개를 합치면
이렇게 쓸 수 있는 거시다.... 이 것 처럼 action value function 도 보면
이렇게 쓸 수 있다.
이제 진짜 마지막으로 Markov Decision Process 에 대해서만 언급하고 마치겠다.
Markov Decision Process는 (State, Action, State Transition Probability Matrix, Reward Function, Discount factor) 로 되어 있는 튜플이다. 어떤 블로그에서는 마지막 Discount Factor 대신에 Starting state distribution 을 넣기도 하던데 왜 그러는지 모르겠다.
중요한 것은 강화학습 문제를 이런 Markov Decision Process 형태로 만들고 문제를 푼다는 것이다. 이 MDP 형태와 위에서 언급한 매우 매우 많은 개념들을 이용해 이제 문제를 푸는 것이다.... 후우