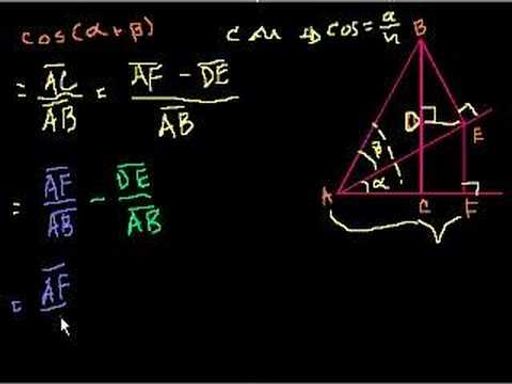Translation Matrix (물체 이동)
Translation Matrix (물체 이동)
(x,y) from origin1 ⇒ (x+a, x+b) from origin 1
[x, y, 1] Vector를 [x+a. x+b, 1]로 ( , )만큼 이동시킨다. 이때 [x, y, 1] 에 1 이 뒤에 붙음으로서 행렬 하나로 이동 연산을 처리할 수 있다.
 Scaling Matrix (물체 크기 변경)
Scaling Matrix (물체 크기 변경)
(2) 원점 기준 Scaling
(2) 점 를 기준으로 도형 Scaling
사각형에게 이 Matrix를 적용할 때, 중심점이 (0,0)이면 아무 문제가 없다.
문제는 도형의 중심점이 Origin Point가 아닐 때 생긴다.
기준점이 0,0인 경우 의도한 대로 정상 작동
그러나 물체의 위치까지 함께 변화하는 문제 발생
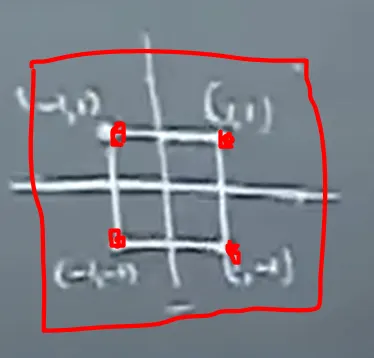
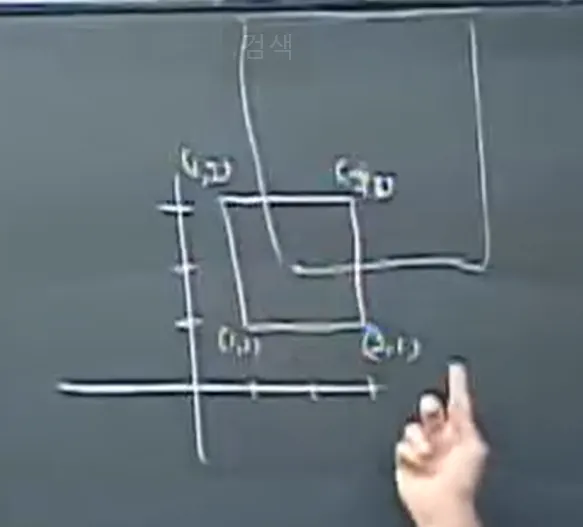
만약 a(1,1) b(1,3) c(3,1) d(3,3) 점을 가진 사각형의 중심축이 (2, 2)라면
a(1,1) → 2* a'(-1, -1) ⇒ a''(-2, -2) → a'''(0, 0)
b(1,3) → 2* b'(-1, 1) ⇒ b''(-2, 2) → b'''(0, 4)
c(3,1) → 2* c'(1, -1) ⇒ c''(2, -2) → c'''(4, 0)
d(3,3) → 2* d'(1, 1) ⇒ d''(2, 2) → d'''(4, 4)
이를 행렬로 표현하면 아래와 같다.
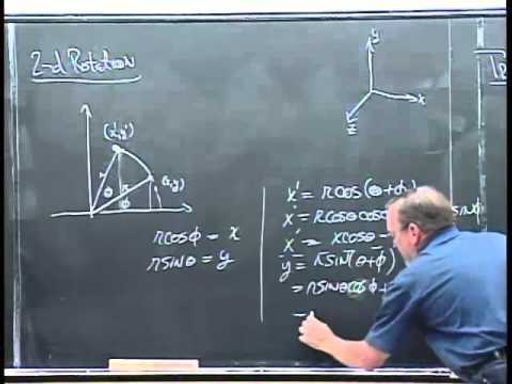
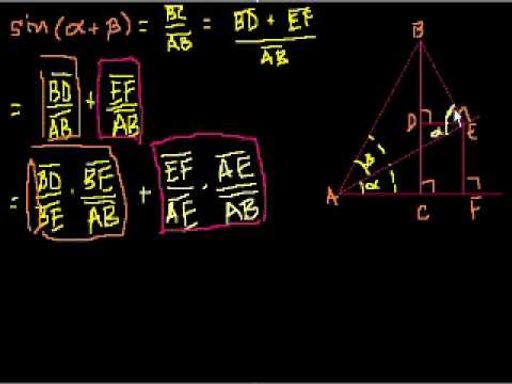
 2D Rotating Matrix (회전 변환)
2D Rotating Matrix (회전 변환)
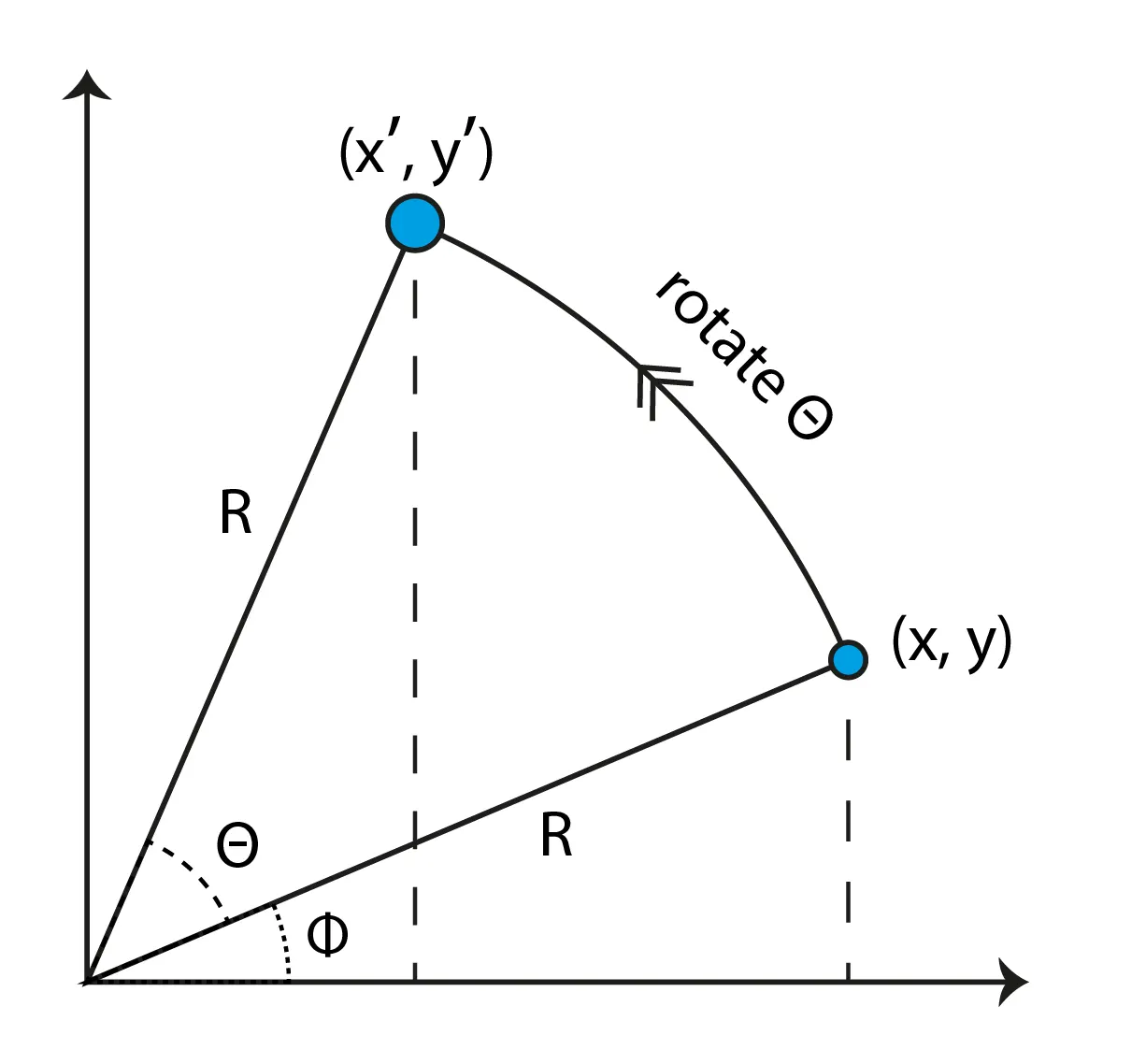
(1) 원점 기준 2D Rotating
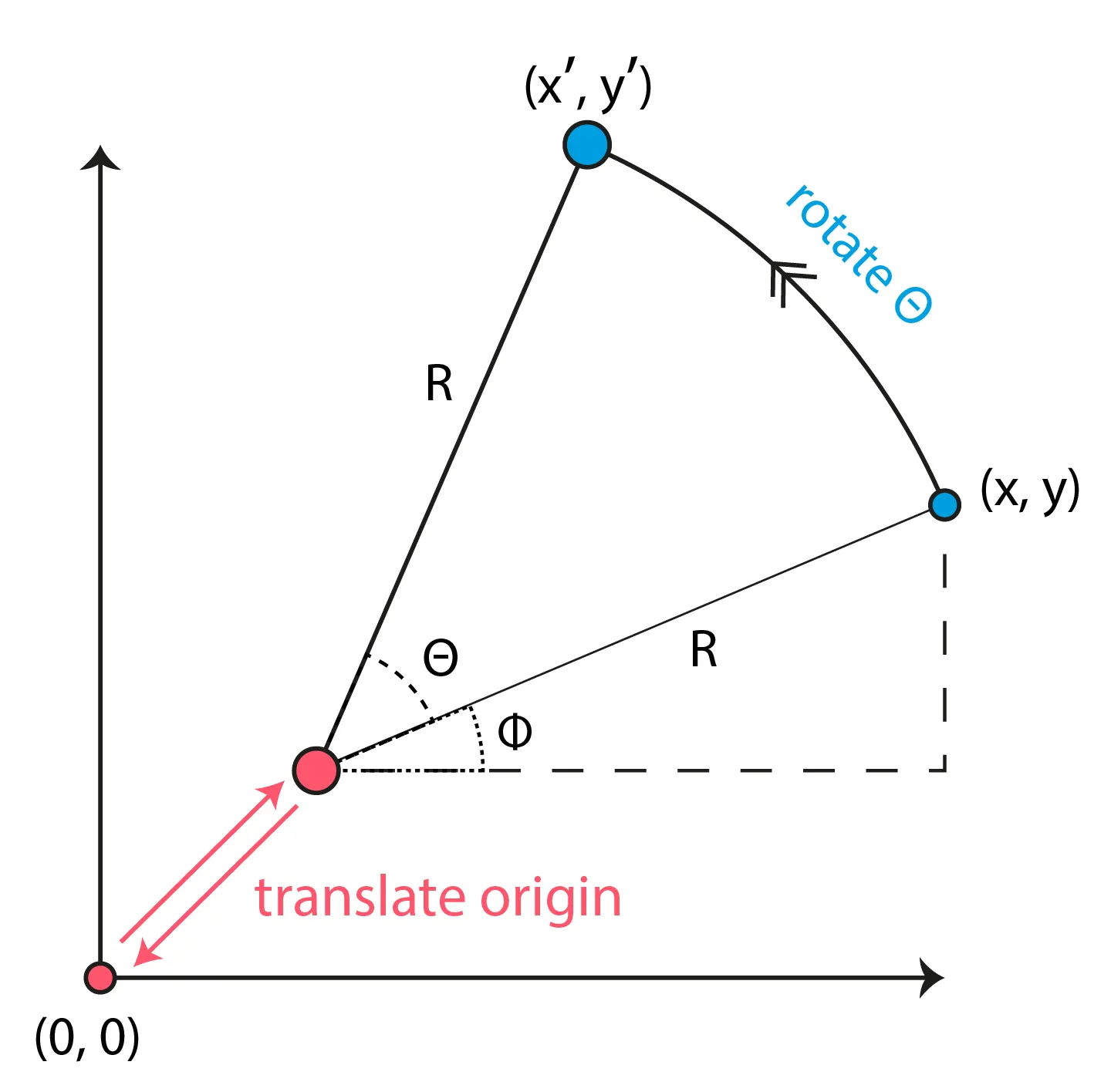
(2) 점 기준 2D Rotating
 3D Rotating Matrix
3D Rotating Matrix
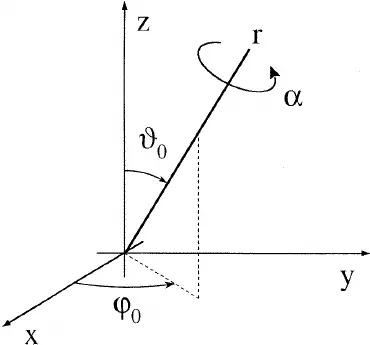
(1) (X, Y, Z) axis 기준 3D Rotating
특성 1) X axis 를 기준으로 회전시, 점의 X값들은 유지된다.
특성 2) Y axis 를 기준으로 회전시, 점의 Y값들은 유지된다.
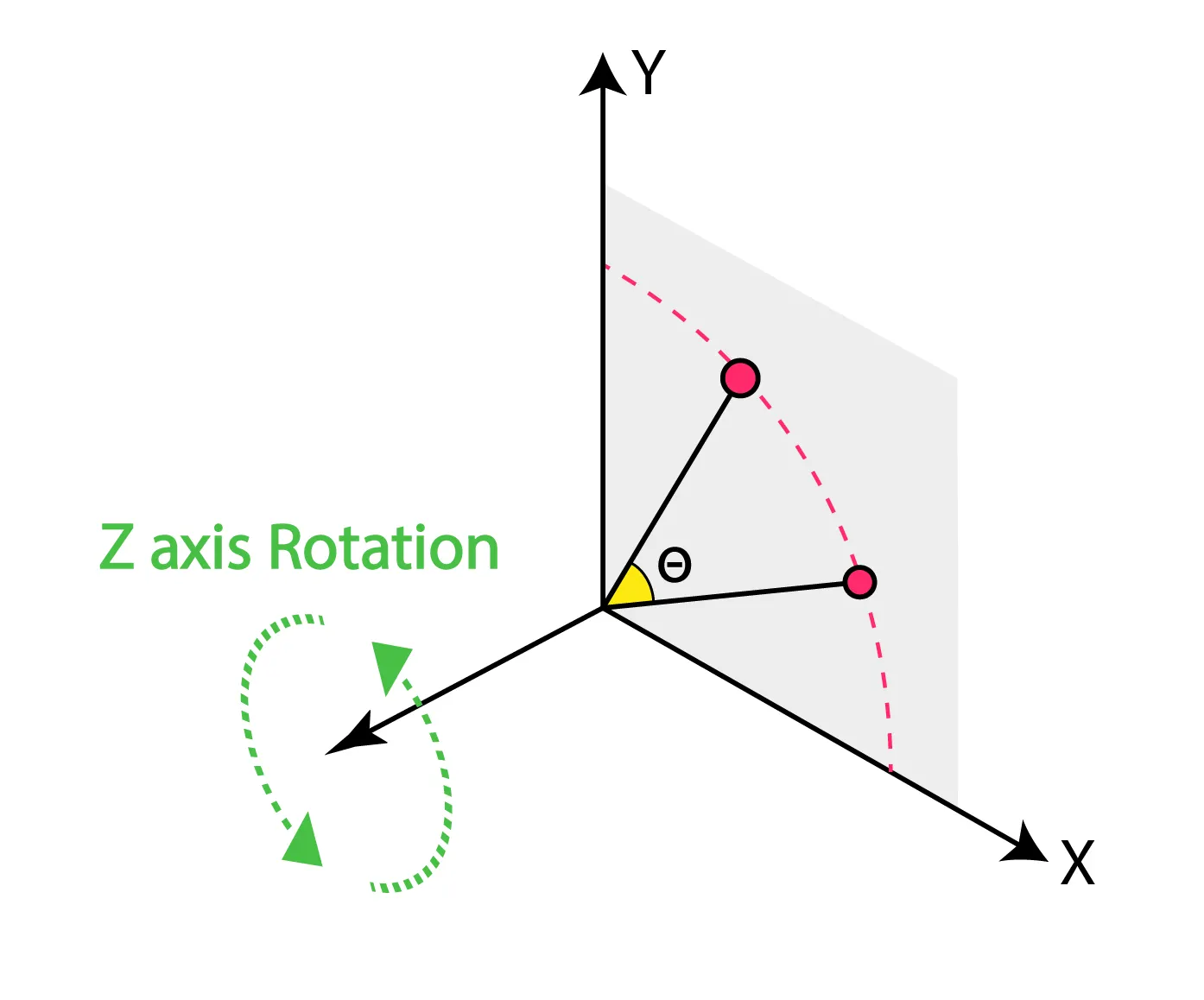
특성 3) Z axis 를 기준으로 회전시, 점의 Z값들은 유지된다.
Z axis 기준 회전시 예시
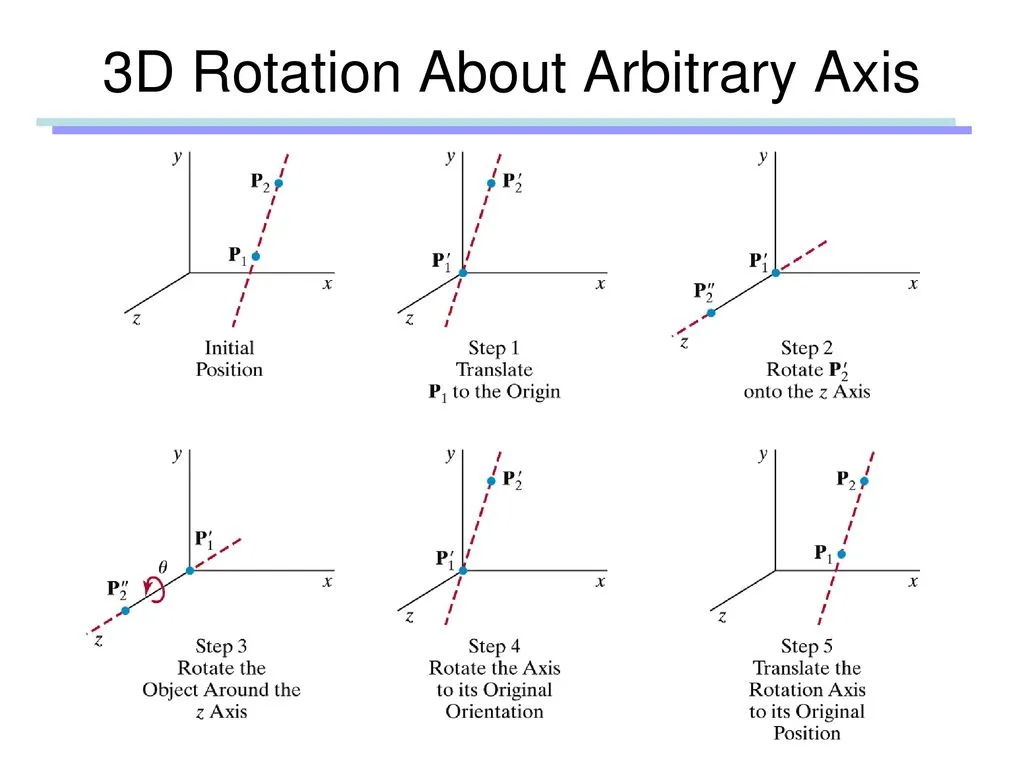
(2) Vector (P1, P2)를 기준으로 3D Rotate (around an Arbitrary Axis)
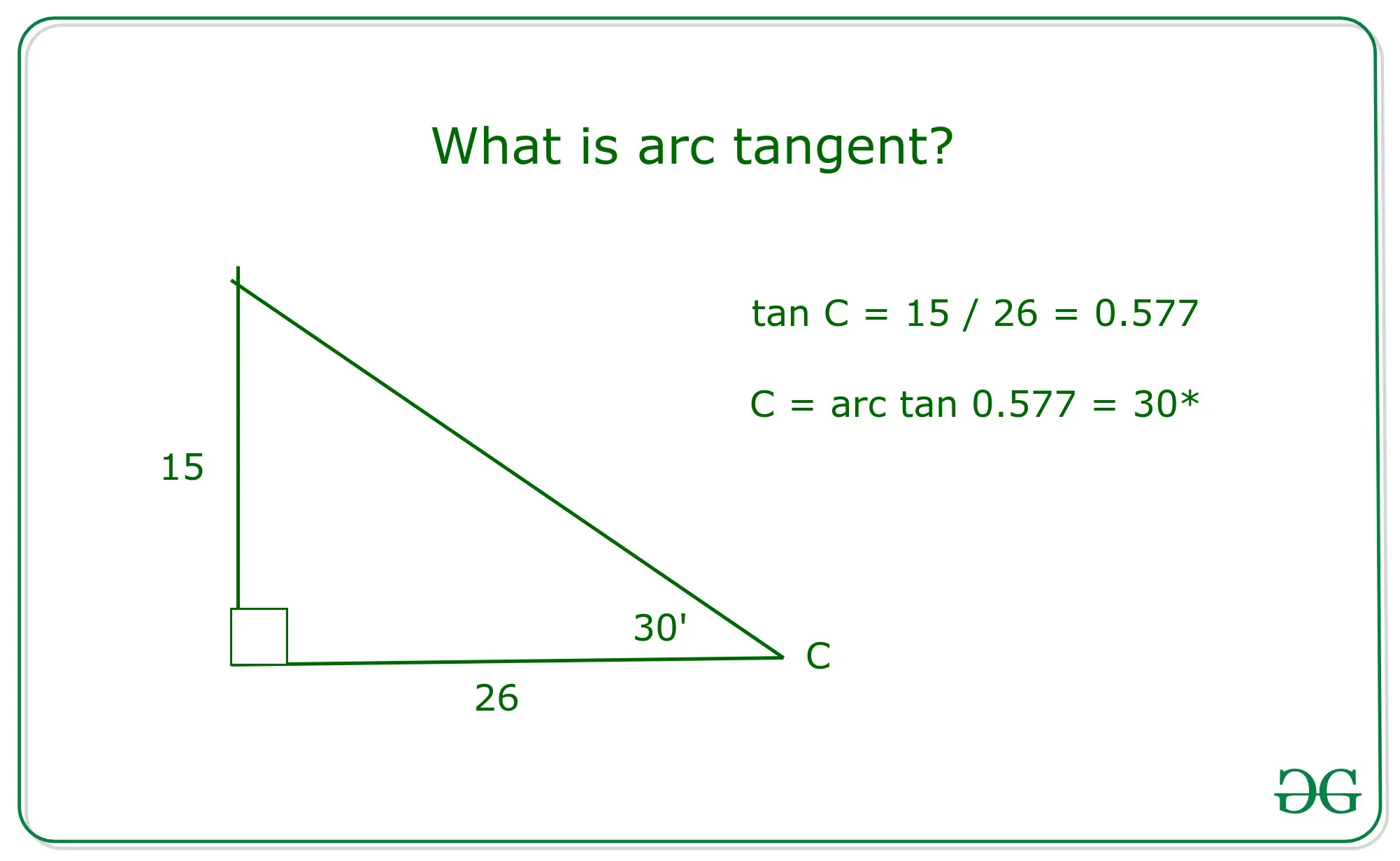
arctan (아크탄젠트)는 (x,0), (0,y) 정보가 있다면 각도를 구할 수 있다.
Rotate around an Arbitrary Axis (xyz축 중 선택)
1.
회전축 벡터의 시작점(P)를 원점으로 이동(Translate)시킨다.
2.
회전축 벡터를 Y Z Axis 평면으로 Rotate 시킨다.
3.
회전축 벡터를 Z Axis로 Rotate 시킨다.
4.
Z Axis를 기준으로 회전시킬 도형을 회전시킨다.
5.
(-) 회전축 벡터를 Z Axis로 복구 Rotate 시킨다.
6.
(-) 회전축 벡터를 Y Z Axis 평면으로 복구 Rotate 시킨다.
7.
(-) 회전축 벡터의 시작점(P)를 원점에서 시작점으로 이동(Translate)시킨다.