예제 : 최단경로
그래프의 간선들에 가중치가 없다면 DFS나 BFS를 이용해 최단거리를 구할 수 있다.
하지만 간선들에 가중치가 존재한다면 단순한 DFS나 BFS로 풀기에는 곤란해진다.
Dijkstra(다익스트라) 알고리즘은 가중치가 있는 그래프의 한 노드에서 다른 모든 노드로 가는 최소 Cost를 구하는 알고리즘이다.
동작 방식
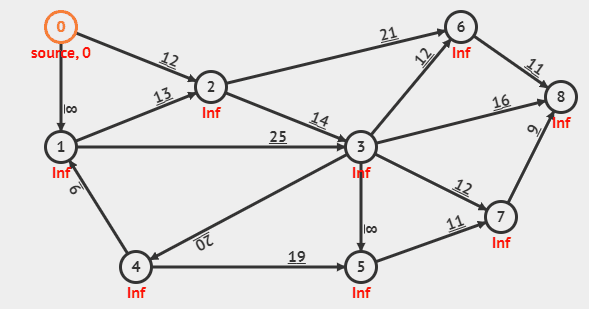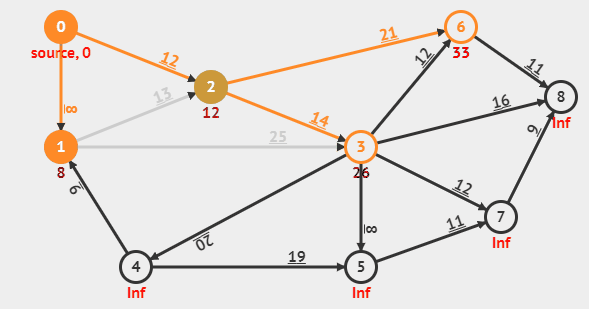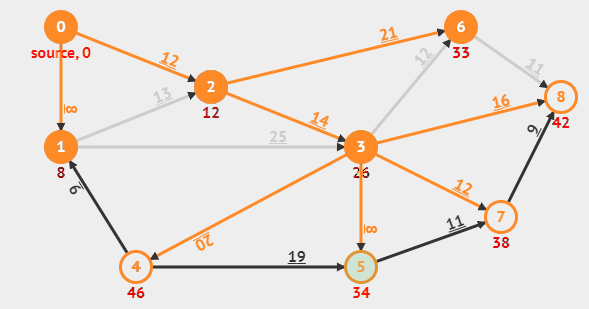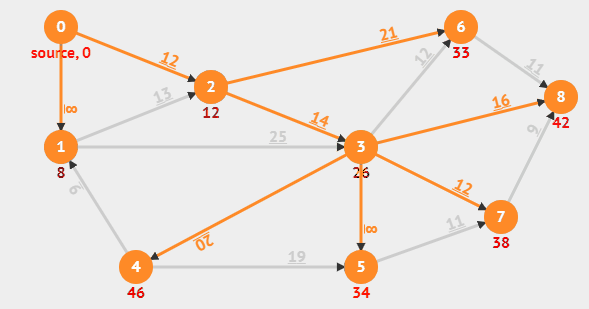
다익스트라의 동작 방식을 gif로 보여주는 예시이다. (위의 동작은 개선된 다익스트라의 동작이다.)
인접 리스트 방식을 이용한 간선 저장
우선 간선에 대한 정보들을 인접 리스트로 저장해야 한다.
vector 선언
#include <vector>
using namespace std;
vector<pair<int, int> > v[N];
C++
복사
이렇게 벡터를 구성하면 N개의 노드들에 대해 각각 간선의 정보를 저장할 수 있다.
만약 0번 노드에서 1번 노드 방향으로 가중치가 8인 간선이 존재한다면
v[0].push_back(1, 8);와 같은 방식으로 저장한다.
가중치가 추가되었을 뿐, 기존 BFS나 DFS와 인접 리스트를 만드는 방식은 크게 다르지 않다.
dist 배열 초기화
가중치가 없는 그래프를 탐색할 때에는 최단거리를 단순히 노드 수를 이용하여 구하였다면, 이제는 가중치의 합끼리 비교해야만 한다.
이를 위해 dist라는 배열을 따로 만들어 적당한 값으로 초기화 해주어야 하는데, dist는 그래프의 최단거리를 구하기 위해 메모이제이션을 사용하는데 필요한 배열이다.
#define INF 1000000000
int dist[N];
void init_dist()
{
int i;
i = 0;
while (i++ < N)
dist[i] = INF;
}
C++
복사
dist 배열은 지속적으로 최솟값으로 갱신되어 나갈 것이기 때문에 충분히 큰 값으로 초기화가 필요하다.
dijkstra 알고리즘 구현
void Dijkstra(int start)
{
int cost, cur;
int ncost, next;
int i;
priority_queue<pair<int, int> > pq;
dist[start] = 0;
pq.push(make_pair(0, start));
while (!pq.empty())
{
cost = -pq.top().first;
cur = pq.top().second;
pq.pop();
i = 0;
while (i < v[cur].size())
{
next = v[cur][i].first;
ncost = v[cur][i].second;
if (dist[next] > cost + ncost)
{
dist[next] = cost + ncost;
pq.push(make_pair(-dist[next], next));
}
i++;
}
}
}
C++
복사
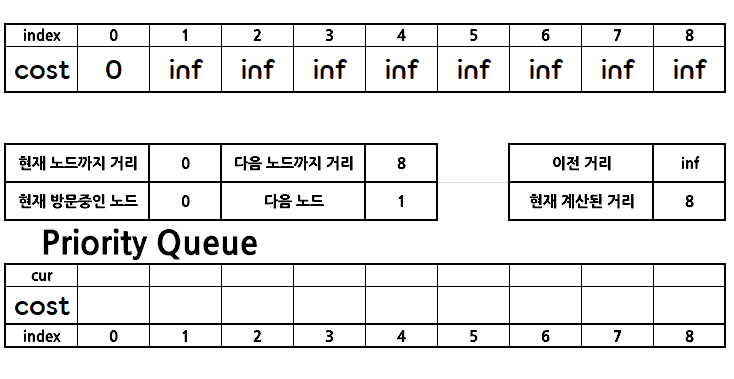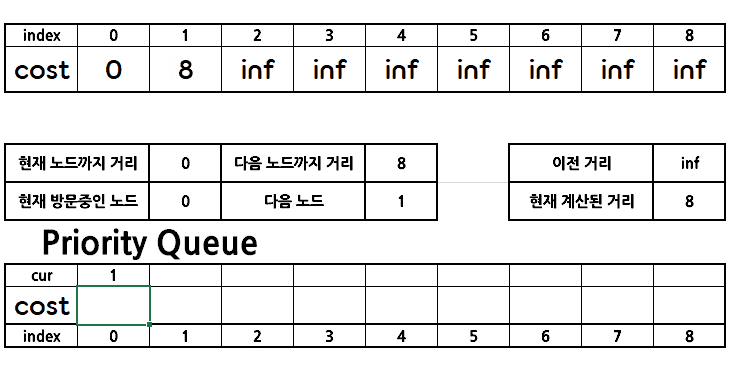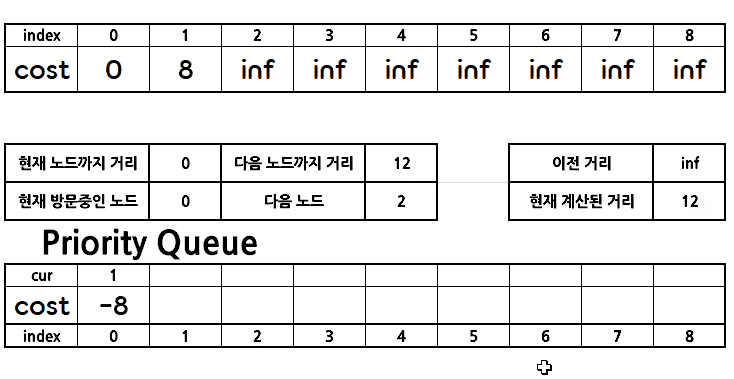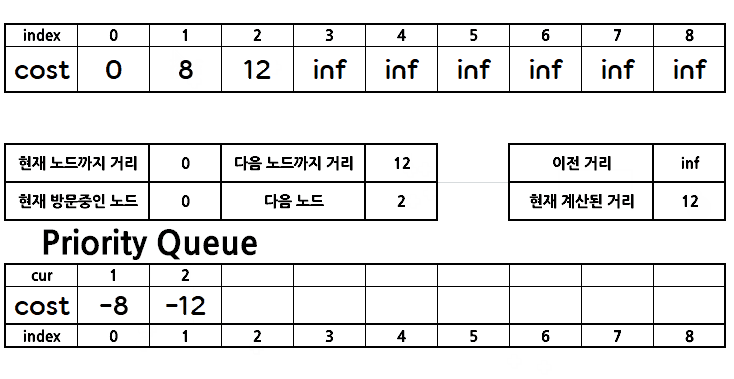
위의 그림과 코드를 이용해서 다익스트라 알고리즘을 파악해보자.
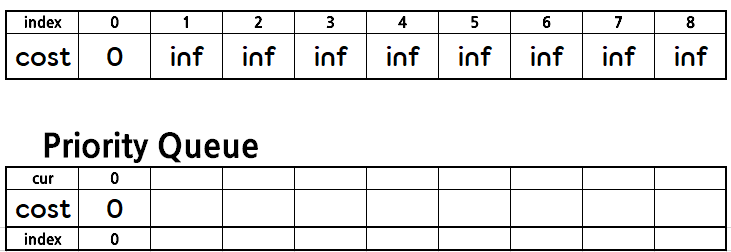
우선 자기 자신으로 가는 거리는 0일 것이므로 다익스트라 알고리즘을 사용하기 전 dist 배열은 아래와 같을 것이다.
우선순위 큐에 자기 자신까지의 거리와 자기 자신의 노드 번호를 넣는다.
그 이후 우선순위 큐에서 우선순위가 가장 높은 pair를 꺼내고, 해당 노드의 인접 리스트에 담겨져 있는 모든 간선들을 확인하며, 코스트가 갱신된다면 인접 리스트에서 간선의 정보를 꺼내 우선순위 큐에 담는다.
위를 반복하며 가중치를 갱신해나간다.
위 과정이 종료되면 0번 노드에서 나머지 모든 노드까지의 거리가 이렇게 저장된다.
우선순위 큐를 사용하는 다익스트라는 언제나 최단거리가 보장된다.
단, 음수 가중치가 존재하는 경우에는 다익스트라 알고리즘을 적용할 수 없다.
예제 : 타임머신
해당 예제는 다익스트라 알고리즘이 아닌 벨만-포드 알고리즘을 이용해야 한다.