5달을 깎은 끝에 얻은 결론이지만, 과정을 설명하기에는 너무 길어 결과만 남겼습니다.
가능한가?
결론부터 말하자면, 이 방법으로 519개까지는 무조건 4000번 미만으로 정렬할 수 있습니다.
아이디어
이는 몇 가지 간단한 아이디어에서 시작합니다.
각 스택의 끝에서 끝으로 자유롭게 이동할 수 있다
스택 A의 top, 스택 A의 bottom, 스택 B의 top, 스택 B의 bottom, 이렇게 총 4가지 위치에서는 서로 다른 곳으로 이동할 수 있습니다.
시작 위치, 끝 위치 | A top | A bottom | B top | B bottom |
A top | - | ra | pb | pb + rb |
A bottom | rra | - | rra + pb | rra + pb + rb |
B top | pa | pa + ra | - | rb |
B bottom | rrb + pa | rrb + pa + ra | rrb | - |
그러므로 3분할 병합정렬, 퀵정렬이 가능합니다.
병합정렬, 퀵정렬, 18가지 방향, 다양한 방법
a + b + c = N개를 정렬하면서 이동하는 방법을 크게 병합정렬과 퀵정렬로 나눌 수 있습니다.
•
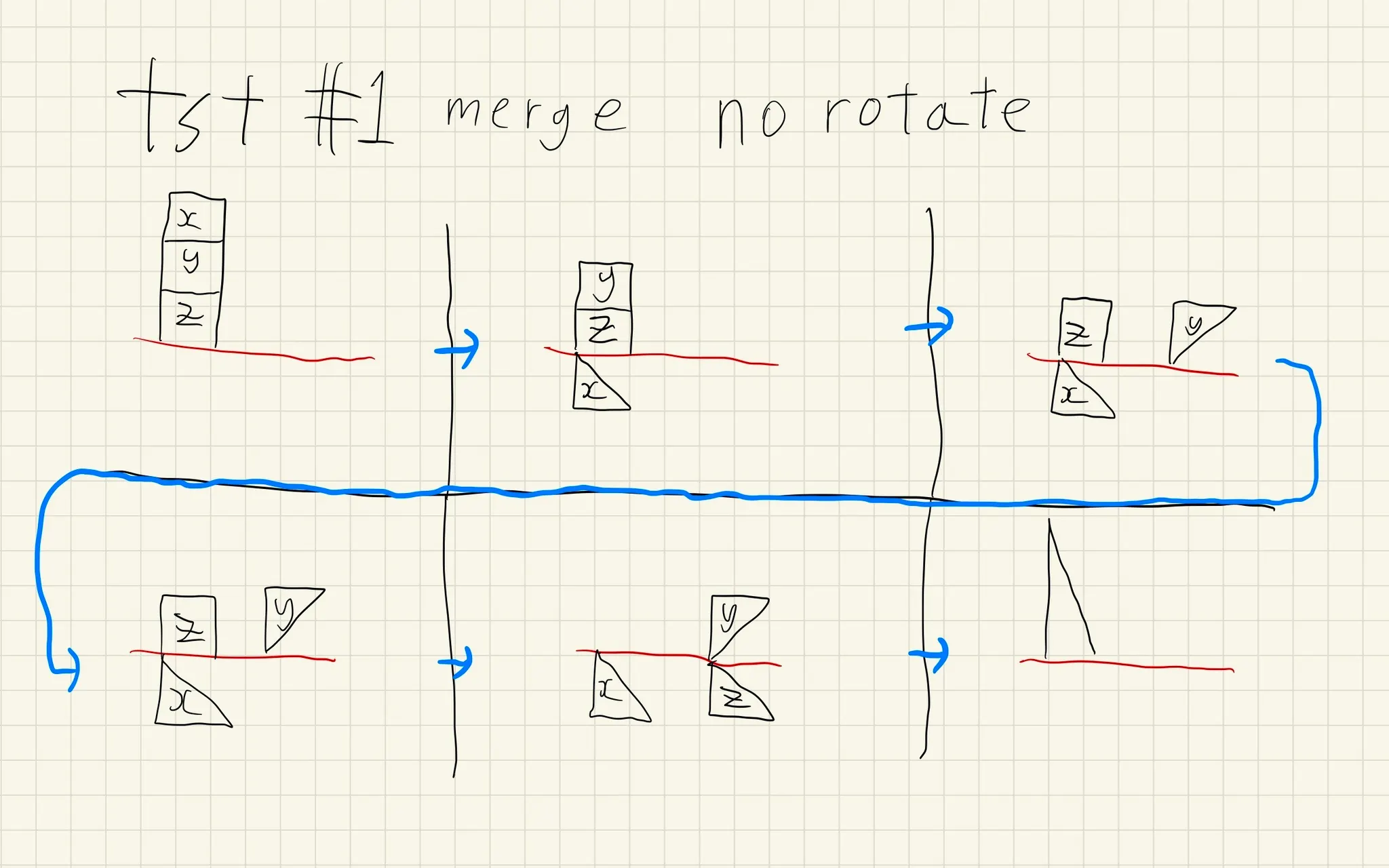
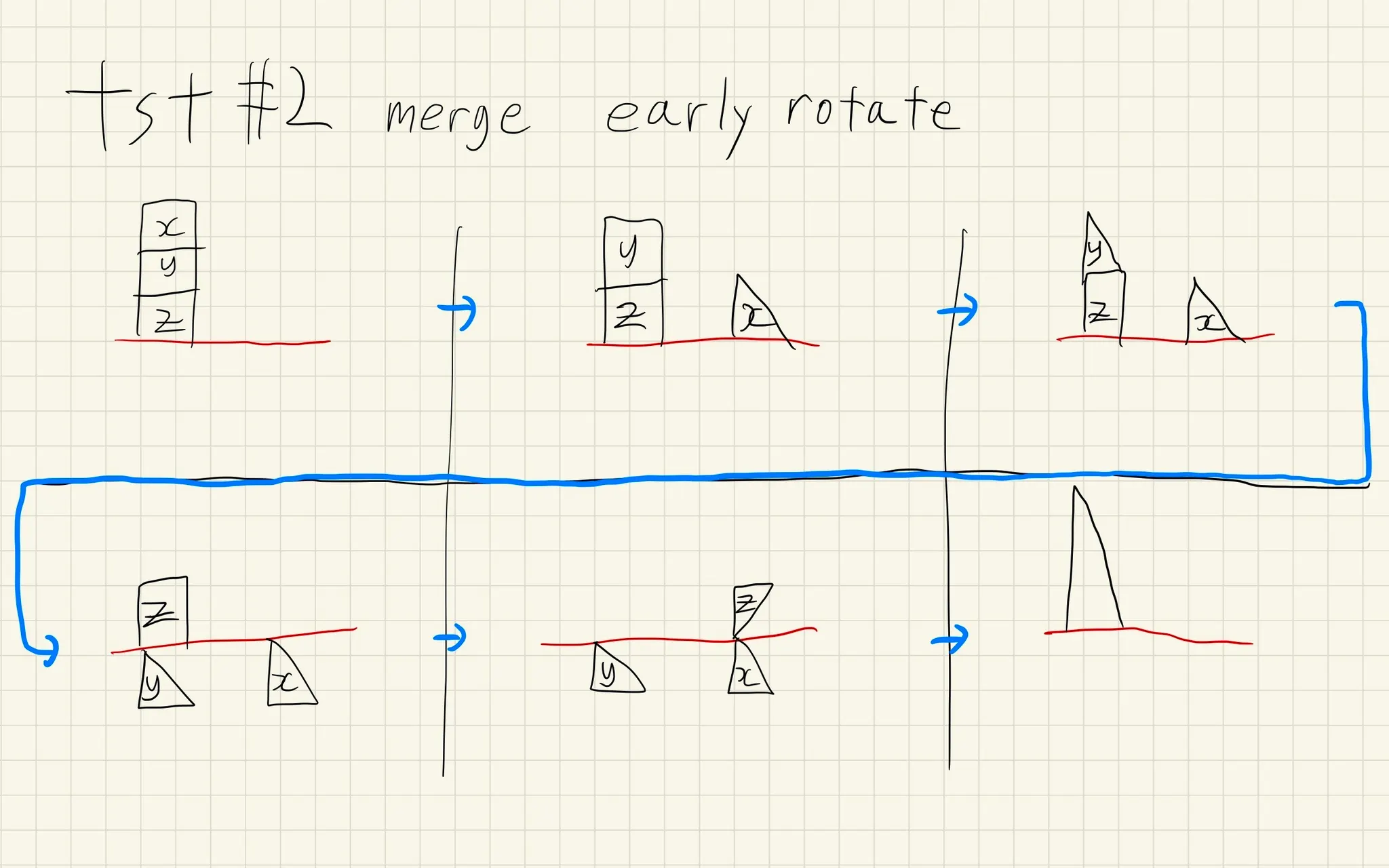
병합정렬
◦
예시: (가)에서 (나)로 정렬
▪
(가)에서 (나)로 a개를 정렬하면서 이동 (재귀적)
▪
(가)에서 (다)로 b개를 정렬하면서 이동 (재귀적)
▪
(가)에서 (가)로 c개를 정렬하면서 이동 (재귀적)
▪
(가), (다), (라)에서 (나)로 병합
•
퀵정렬
◦
예시: (가)에서 (가)로 정렬
▪
(가)에서 크기에 따라 큰 것 a개를 (나), 작은 것 c개를 (라), 중간 b개를 (다)로 정렬하면서 이동
▪
(나)에서 (가)로 a개를 정렬하면서 이동 (재귀적)
▪
(다)에서 (가)로 b개를 정렬하면서 이동 (재귀적)
▪
(라)에서 (가)로 c개를 정렬하면서 이동 (재귀적)
각 위치는 스택 A, B의 top, bottom일 수도 있고 top이면서 bottom일 수도 있습니다.
방향이 같아도 여러가지 방법이 있지만, 어떤 방법이 가장 효율적일지는 미리 알 수 없습니다.
개수와 방향에 따라 효율적인 정렬 방법/개수가 다르다
예를 들어 스택 A의 top에서 스택 A의 top으로 정렬하면서 이동하는 경우 아래 두 가지 방법이 있을 수 있습니다.
두번째 방법(#2)은 rr을 활용했습니다.
제가 찾은 방법은 6가지인데, 실제로 같은 방향이라도 개수에 따라 효율적인 방법이 달랐습니다.
방법
(ㄱ) - 우선 무차별 대입으로 몇 개까지는 항상 최적의 경로로 정렬되도록 하드코딩할 수 있습니다.
// 중략
"\2\2\2\2\5\13\5\10\5\10\1\1\1\1\6\6\6\6",
// 9 8 7 6 5 4 2 3 1을 a의 top/bottom에서 a의 top/bottom으로 이동하려면
// pb pb pb pb ss rrr ss rr ss rr pa pa pa pa ra ra ra ra
"\2\2\2\2\2\5\11\13\1\1\1\6\10\1\1\6\6\6",
// 9 8 7 6 5 4 3 1 2을 a의 top/bottom에서 a의 top/bottom으로 이동하려면
// pb pb pb pb pb ss rra rrr pa pa pa ra rr pa pa ra ra ra
"\2\2\2\2\2\3\13\13\5\1\1\1\10\1\1\6\6\6\6",
// 9 8 7 6 5 4 3 2 1을 a의 top/bottom에서 a의 top/bottom으로 이동하려면
// pb pb pb pb pb sa rrr rrr ss pa pa pa rr pa pa ra ra ra ra
// 후략
C
복사
무차별 대입으로 찾은 하드코딩된 데이터 예시
(ㄴ) - 다음으로는 무차별 대입과 DP를 통해 개수와 방향에 따라 어떤 방법으로, 어디로 몇 개를 보내는 게 효율적일지도 몇 개까지는 하드코딩할 수 있습니다.
{
// 5000개를 정렬할 때 방향별로 어떤 방법을 써야 몇번만에 정렬이 완료될지
{{{1690, 2193, 1117}, 55845}, ps_solve_tst_merge_no_rotate_solve},
{{{1857, 2431, 712}, 53514}, ps_solve_txt_merge_twist_solve},
{{{1427, 519, 3054}, 57664}, ps_solve_tsb_merge_solve},
{{{1188, 1968, 1844}, 54224}, ps_solve_txb_merge_straightforward_solve},
{{{1631, 766, 2603}, 55779}, ps_solve_tot_merge_no_rotate_solve},
{{{878, 2358, 1764}, 53452}, ps_solve_tos_merge_solve},
{{{2849, 570, 1581}, 57387}, ps_solve_tob_merge_solve},
{{{1968, 712, 2320}, 54505}, ps_solve_sss_merge_solve},
{{{2088, 712, 2200}, 53565}, ps_solve_sxs_merge_straightforward_solve},
{{{736, 2355, 1909}, 54176}, ps_solve_sot_quick_solve},
{{{386, 2297, 2317}, 53784}, ps_solve_sob_quick_solve},
{{{519, 1427, 3054}, 57664}, ps_solve_bst_quick_solve},
{{{1256, 700, 3044}, 56586}, ps_solve_bxt_merge_twist_solve},
{{{2963, 1493, 544}, 58996}, ps_solve_bsb_merge_solve},
{{{296, 1415, 3289}, 56158}, ps_solve_bxb_quick_twist_solve},
{{{602, 1808, 2590}, 57387}, ps_solve_bot_merge_no_rotate_solve},
{{{599, 2335, 2066}, 55613}, ps_solve_bos_merge_solve},
{{{386, 1390, 3224}, 59369}, ps_solve_bob_merge_solve},
},
C
복사
무차별 대입과 DP로 구한 개수/방향별 최적의 개수/방법 데이터 예시
이제 런타임에서는 이렇게 정해진 방법대로 정렬하면 됩니다.
일정 개수 (ㄱ) 이하는 하드코딩된 최적의 경로로, 또 일정 개수 (ㄴ) 이하는 최적의 개수/방법으로, 그 이상은 (ㄴ)의 마지막 비율대로…
마무리
저는 블랙홀이 부족해서 이 방법을 고안만 하고 구현은 아직 못 했습니다.
아마 이 방법대로 구현한다면 세계 1등일지도…?
생각하는 즐거움을 박탈하고 싶지 않아 최소한의 정보만 남겼습니다. 여러분도 한 번 생각해보세요!
그리고 혹시 더 빠르게 정렬할 방법을 찾으셨다면 댓글 남겨주시면 감사하겠습니다.