Introduction
Tree는 Graph 자료구조의 한 부분입니다. 트리는 가계도, 조직도 등과 같은 계층적인 구조를 표현할 때 사용할 수 있는 자료구조입니다. 그리고 트리는 한 개 이상의 노드로 이루어진 사이클이 없는 연결 그래프입니다.
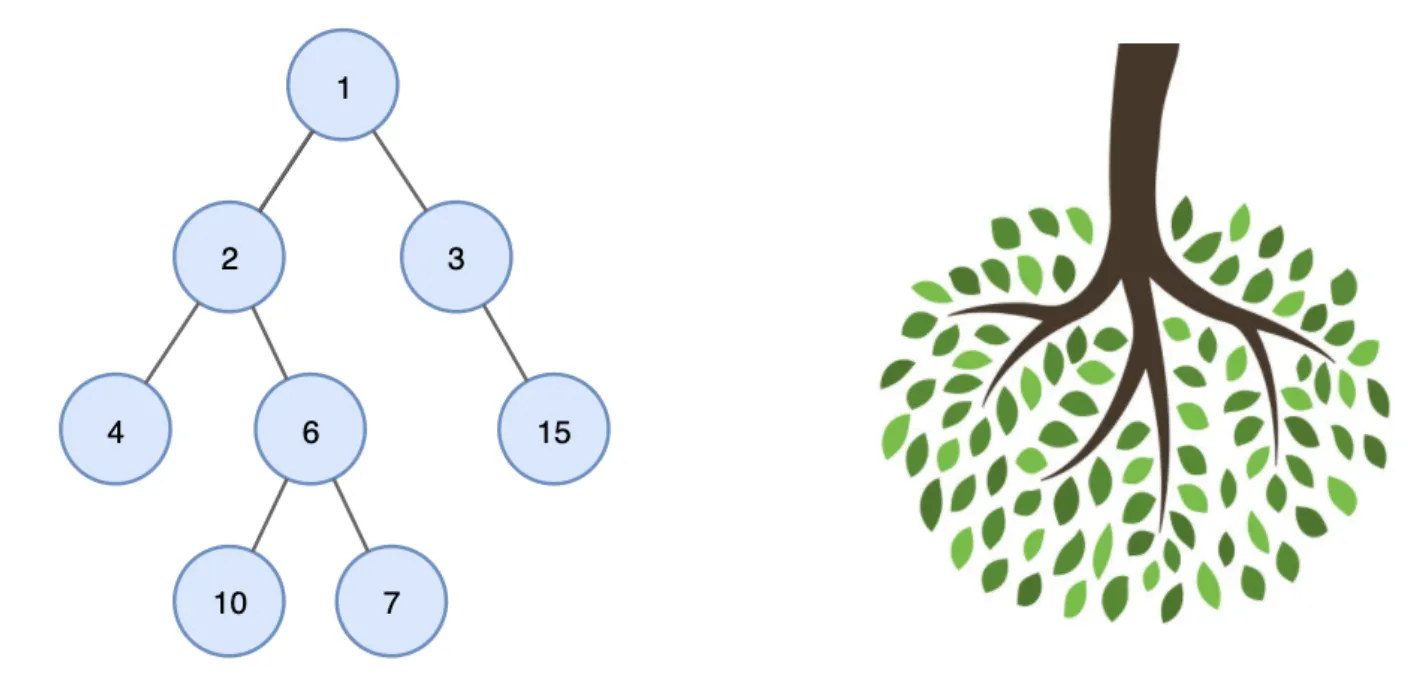
트리는 이름 그대로 뿌리와 잎사귀를 가지고 있습니다. 하지만 우리가 상상하는 트리의 방향과는 반대입니다. 아래의 그림과 같이 뿌리가 위, 잎이 아래에 위치하고 있습니다.
Example
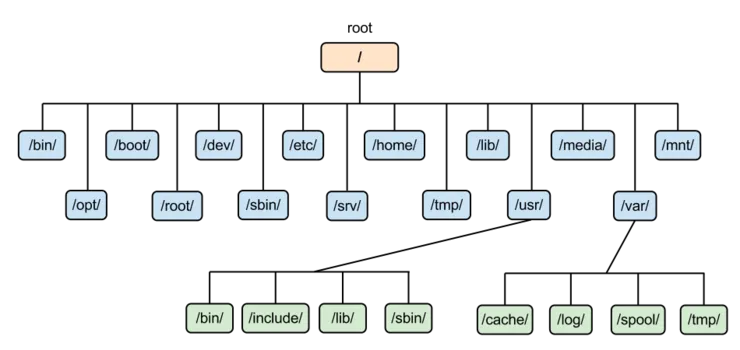
앞에서 언급한 것처럼 트리 자료구조는 디렉토리 구조에 실제로 사용됩니다. 최상위 디레곹리가 루트 노드이고, 그 아래에 하위 디렉토리가 존재하며, 이러한 하위 디렉토리는 더 깊은 수준의 디렉토리로 확장될 수 있습니다.
또한 인터넷 라우팅에 이 트리 자료구조가 사용될 수 있습니다. 라우팅은 데이터 패킷이 목적지로 전송되는 경로를 결정하는 과정입니다. 라우팅 테이블은 트리 자료구조로 구현될 수 있으며, 각 노드는 네트워크의 서브넷을 나타내고 자식 노드는 더 세분화된 서브넷을 나타냅니다. 이를 통해 데이터 패킷을 경로를 효율적으로 결정할 수 있습니다.
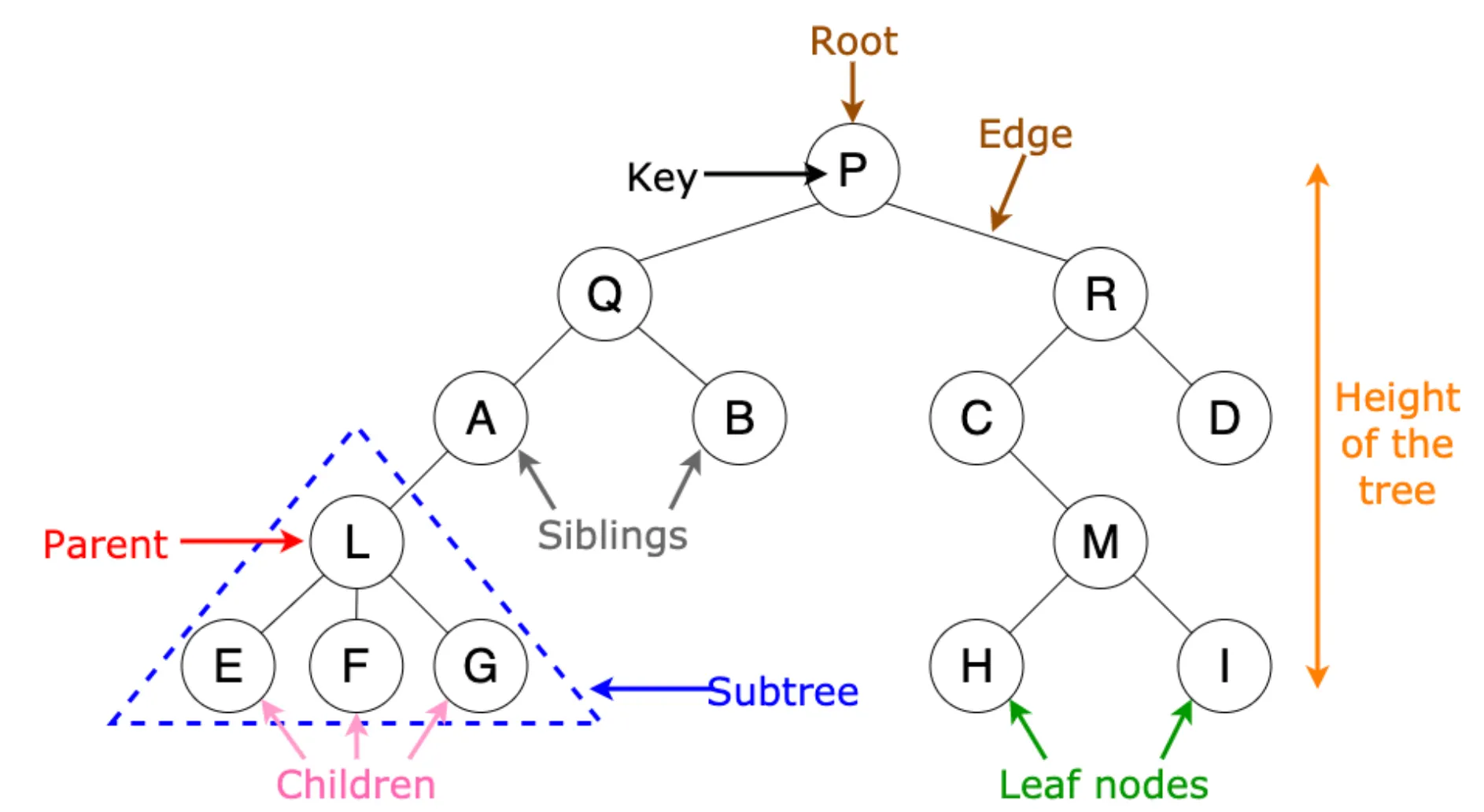
Terminology
루트 노드(root node)
•
부모가 없는 최상위 노드
•
트리의 시작점
자녀(child)노드
•
모든 노드는 0개 이상의 자녀 노드를 가진다.
부모(parent)노드
•
자녀 노드를 가지는 노드
형제(sibling)노드
•
같은 부모를 가지는 노드들
조상(ancestor)노드
•
부모 노드를 따라 루트 노드까지 올라가며 만나는 모든 노드
자손(descendant)노드
•
자녀 노드를 따라 내려가며 만날 수 있는 모든 노드
내부(internal)노드
•
자녀 노드를 가지는 노드
•
a.k.a branch node, inner node
외부(external)노드
•
자녀 노드가 없는 노드
•
a.k.a 단말노드(leaf node), outer node, terminal node(단말 노드)
경로(path)
•
한 노드에서 다른 노드 사이의 노드들의 시퀀스(sequence)
•
ex) 2에서 7로의 경로 : 2 - 5 - 7
경로 길이(lenth of path)
•
경로에 있는 노드들의 수
•
ex) 2 - 5 - 7 이면 3
깊이(depth)
•
루트 노드부터 해당 노드까지의 거리(루트노드의 깊이는 0)
트리의 깊이(depth)
•
트리에 있는 노드의 깊이 중 가장 큰 깊이
높이(height)
•
깊이 중 최댓값
•
간선 수로 하지 않고 노드의 개수로 높이를 계산할 때는 -1 해준다.
트리의 높이( height)
•
트리에서 나타내는 높이
간선(edge)
•
노드와 노드를 연결하는 선
•
구현 관점에서 레퍼런스를 의미
•
a.k.a link, branch
차수(degree)
•
각 노드에서(자식 방향) 뻗어나온 간선 개수
트리의 차수(degree)
•
트리에 있는 노드들의 차수 중 가장 큰 차수
거리(distance)
•
두 노드의 최단 경로의 간선 수
노드의 레벨(level)
•
노드와 루트 노드 사이의 경로에서 간선(edge)의 수
•
level을 0이 아니라 1부터 시작하는 경우도 있다.
width
•
임의의 레벨에서 노드의 수
크기(size)
•
노드의 크기 : 자신을 포함한 자손 노드의 수
•
트리의 크기 : 트리에 포함된 모든 노드의 개수
Attribute
•
루트 노드는 하나만 존재한다.
•
사이클(cycle)이 존재하지 않는다.
•
자녀 노드는 하나의 부모 노드만 가진다.
•
데이터를 순차적으로 저장하지 않는 비선형(nonlinear) 구조다.
•
트리에 서브 트리가 있는 재귀적 구조다.
•
계층적 구조이다.
•
노드의 개수가 N개라면, 간선(edge)의 개수는 N - 1 개이다.
•
노드를 중복해 방문하지 않으면, 노드간의 경로는 유일하다.
•
균형이 잡혀있다면, 탐색에 의 수행속도를 가진다.
Binary tree
type
이진 트리는 자식 노드가 최대 두 개로 이루어진 트리입니다. 이진트리의 종류는 다음과 같습니다.
•
fully binary tree: 정이진트리
•
complete binary tree: 완전이진트리
•
balanced binary tree: 균형이진트리
fully binray tree
정이진트리는 모든 레벨에서 노드들이 완전히 채워져 있는 이진 트리를 말합니다. 즉, 잎노드를 제외한 모든 노드들은 자식 노드를 모두 2개씩 가지고 있습니다.
정이진트리의 장점은 트리의 구조가 간단하고 효율적인 연산을 제공한다는 것입니다. 그러나 노드의 개수가 항상 2의 거듭제곱이어야 하기 때문에 데이터의 개수에 따라 비어있는 노드가 발생할 수 있습니다. 따라서 데이터의 동적인 추가나 삭제에 제한이 있을 수 있습니다.
레벨 | 노드수 |
0 | 2^0 |
1 | 2^1 |
2 | 2^2 |
… | … |
𝑘 | 2^𝑘 |
total | 2^(𝑘+1) − 1 |
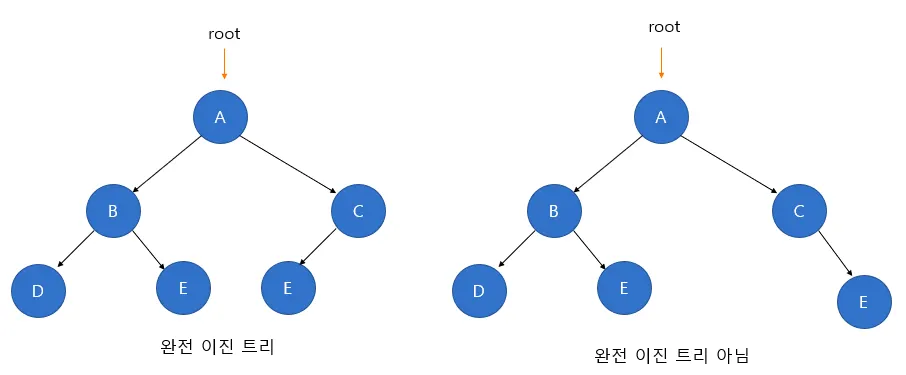
complete binary tree
완전이진트리는 노드들이 왼쪽에서 오른쪽으로 순서대로 채워진 이진 트리를 말합니다. 정이진트리와는 다르게 마지막 레벨을 제외하고 모든 레벨에서 노드들이 가득 차 있고, 마지막 레벨에서 노드들이 왼쪽부터 순서대로 채워져있습니다.
노드의 추가는 마지막 레벨의 가장 오른쪽 노드 다음부터 추가되며, 삭제할 때는 마지막 레벨에서 가장 오른쪽 노드부터 순서대로 왼쪽으로 삭제됩니다.
와전 이진 트리는 배열을 사용하여 구현할 수 있습니다. 노드들을 배열에 순서대로 저장하면, 각 노드의 인덱스와 부모, 자식 노드들의 인덱스 관계를 쉽게 파악할 수 있습니다. 이러한 특성으로 인해 완전이진트리는 메모리를 효율적으로 사용할 수 있으며, 배열 기반의 힙 자료구조 등에 활용됩니다.
완전이진트리의 탐색, 삽입, 삭제, 추가의 연산 시간은 O(lon n)입니다. 따라서 완전 이진 트리에 비해 구현이 간단하고 효율적인 연산을 제공하는 장점이 있습니다.
balanced binary tree
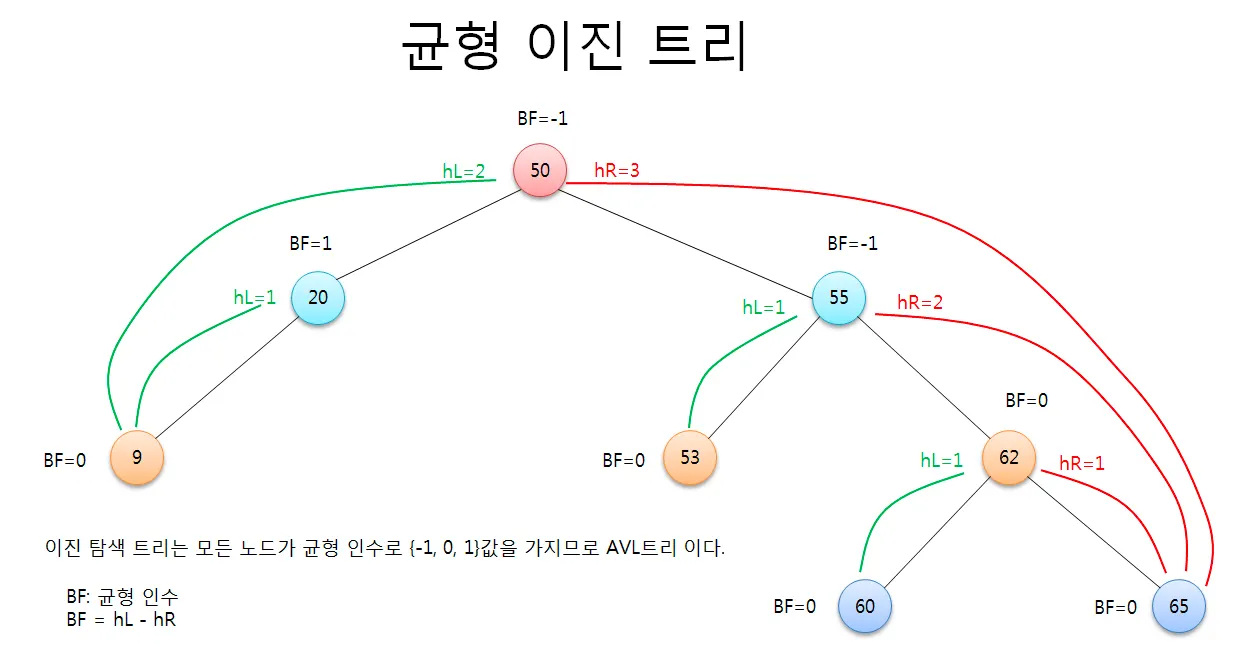
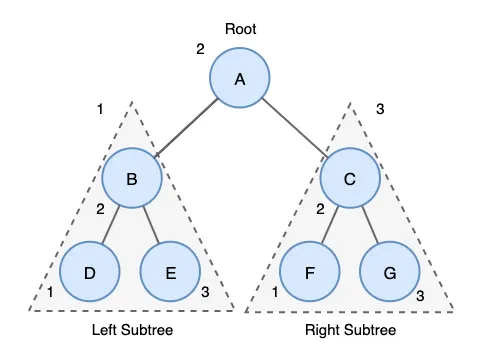
균형이진트리는 모든 노드의 왼쪽 서브트리와 오른쪽 서브트리의 높이 차이가 1 이하인 이진 트리를 말합니다. 즉, 어떤 노드를 기준으로 왼쪽 서브트리와 오른쪽 서브트리의 높이를 비교했을 때, 이 차이가 최대 1 입니다.
일반적으로 균형 이진 트리의 탐색, 삽입, 삭제 연산은 시간 복잡도가 O(log n)으로 매우 효율적입니다. 그러나 균형을 유지하기 위한 회전 연산이 필요하므로 이진 트리에 비해 구현이 복잡할 수 있습니다.
균형 이진 트리의 예시는 다음과 같습니다.
•
AVL tree
•
red-black tree
•
B tree
배열로 이진트리 표현방법
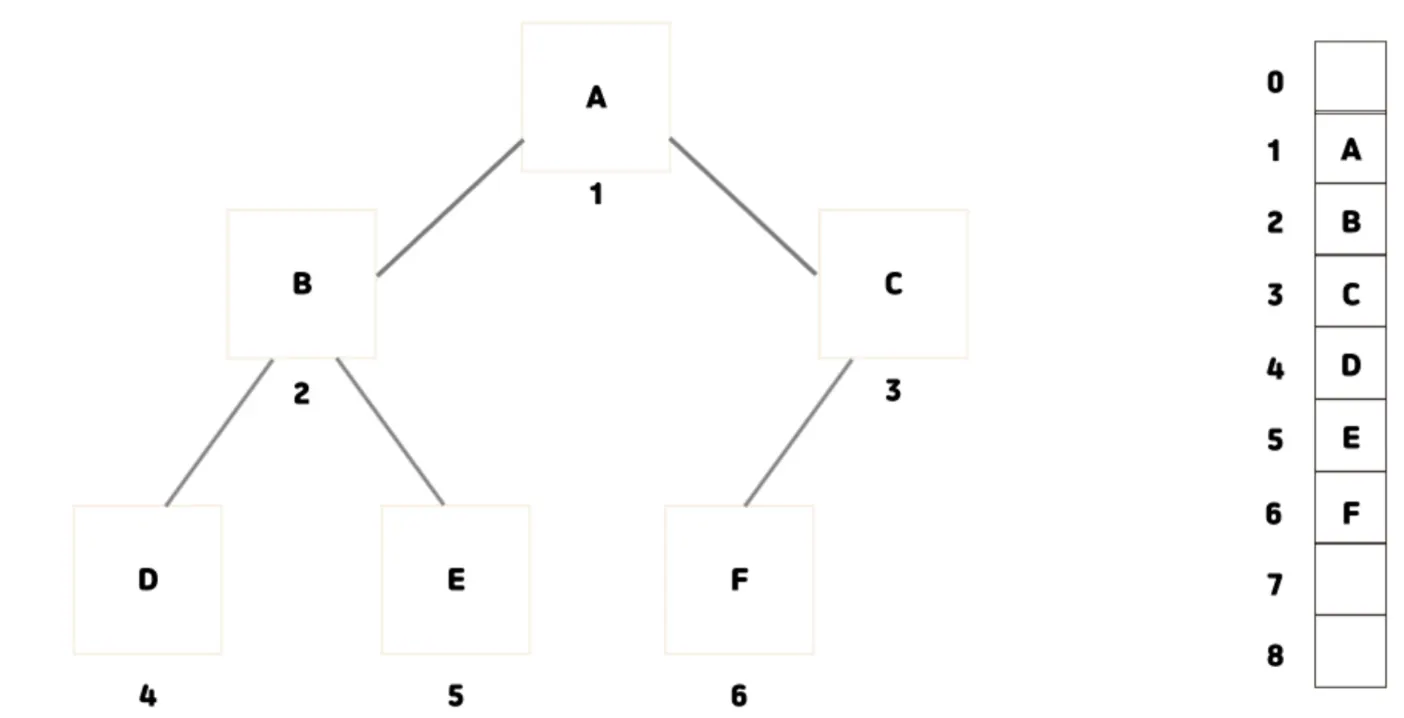
배열을 이용하는 방법은 주로 포화 이진 트리나 완전 이진 트리인 경우 많이 쓰입니다.
저장하고자 하는 이진 트리를 완전 이진 트리라고 가정하고 이진트리의 깊이가 개의 공간을 연속적으로 할당한 다음, 완전 이진 트리의 번호대로 노드들을 저장합니다.
부모의 번호 * 2 = 왼쪽 자식의 번호
부모의 번호 * 2 + 1 = 오른쪽 자식의 번호
라는 공식을 배열 표현법에서 적극 활용됩니다.
여기서 베열의 0번 인덱스를 사용하지 않는 이유는 계산의 복잡함을 방지하기 위함입니다. 만약 0번 인덱스를 사용하게 되면 0이 루트 노드의 번호가 될것이고 위에서 언급한 공식이 성립이 되지 않습니다.
tree traversal
트리 순회란 트리의 각 노드를 체계적으로 방문하는 과정을 말합니다. 하나도 빠뜨리지 않고 정확히 한번만 중복없이 방문해야 합니다. 노드를 방문하는 순서에 따라 그 방법의 종류를 나눌 수 있습니다. 순서에 따라 세 가지로 나눌 수 있습니다.
•
전위 순회
•
중위 순회
•
후위 순회
preorder (Depth-first traversal)
1.
루트 노드를 방문한다.
2.
왼쪽 서브 트리르 전위 순회한다.
3.
오른쪽 서브트리를 전위 순회한다.
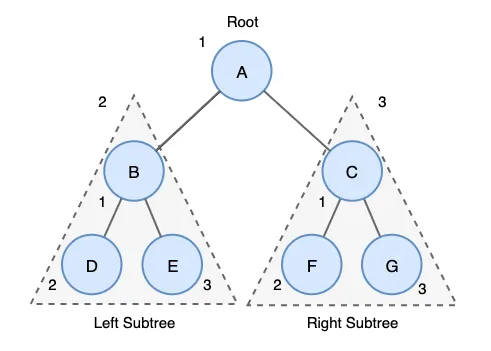
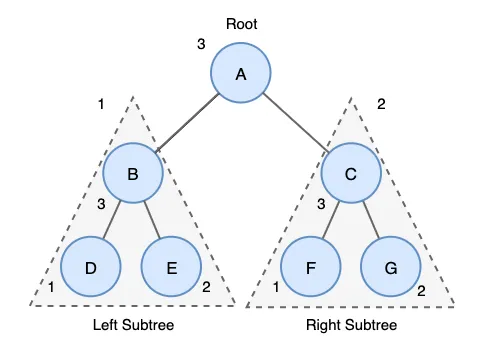
위 트리에 전위 순회 결과는 다음과 같습니다.
A→B→D→E→C→F→G
inorder
중위 순회는 왼쪽 오른쪽 대칭 순서로 순회를 하기 때문에 대칭 순회라고도 합니다. 중위 순회는 이진 탐색트리에서 오른차순 또는 내림차순으로 값을 가져올 때 사용합니다.
1.
왼쪽 서브 트리를 중위 순회한다.
2.
루트 노드를 방문한다.
3.
오른쪽 서브 트리를 중외 순회한다.
위 트리에 중위 순회 결과는 다음과 같습니다.
D→B→E→A→F→C→G
postorder traversal
후위 순회는 트리를 삭제하는데 주로 사용됩니다. 이유는 부모 노드를 삭제하기 전에 자식 노드를 삭제하는 순으로 노드를 삭제해야 하기 때문입니다.
1.
왼쪽 서브 트리를 후위 순회한다.
2.
오른쪽 서브 트리를 후위 순회한다.
3.
루트 노드를 방문한다.
위 트리에 중위 순회 결과는 다음과 같습니다.
D→E→B→F→G→C→A
Trie tree 구현
상황
00플랜트라는 어플리케이션에 식물 검색 기능이 있습니다. 이 식물 검색 기능은 현저히 떨어집니다. 왜냐하면 식물의 이름을 사전에 등록된 대로 정확히 넣어야 검색이 가능하기 때문입니다. 사용자가 식물을 검색을 할 때는 이름을 완벽히 모르는 경우도 있기 때문에 자동 완성 기능이나, 문자열의 일부만 넣어도 검색이 되도록 해야합니다. 사용자 경험 측면에서 단점이 가득한 식물 검색 기능을 개편하려고 합니다.
문제점
지금 어플리케이션에서 사용하는 식물 데이터 구조는 배열입니다. 데이터가 쌓이면 쌓일수록 검색 속도가 느려지며 일일이 문자열을 검색해야 합니다. 그리고 문자열이 정확하게 일치하지 않는다면 검색도 되지 않습니다. 이를 해결하기 위해 트라이 자료구조를 사용하려고 합니다.
트라이(trie) 자료구조
트라이(retrieval tree) 자료구조는 문자열을 저장하고 효율적으로 탐색하기 위한 트리입니다. 우리가 사용하는 검색 시스템의 자동완성 기능, 사전 검색에서 문자열을 탐색하는데 특화되어 있습니다. 배열은 O(n)이지만 트라이 자료구조는 해당하는 문자열이 있다면 O(L)로 탐색할 수 있습니다.
구현 목표
1.
문자열 삽입 기능
2.
문자열 검색 기능
트라이 자료구조 알아보기
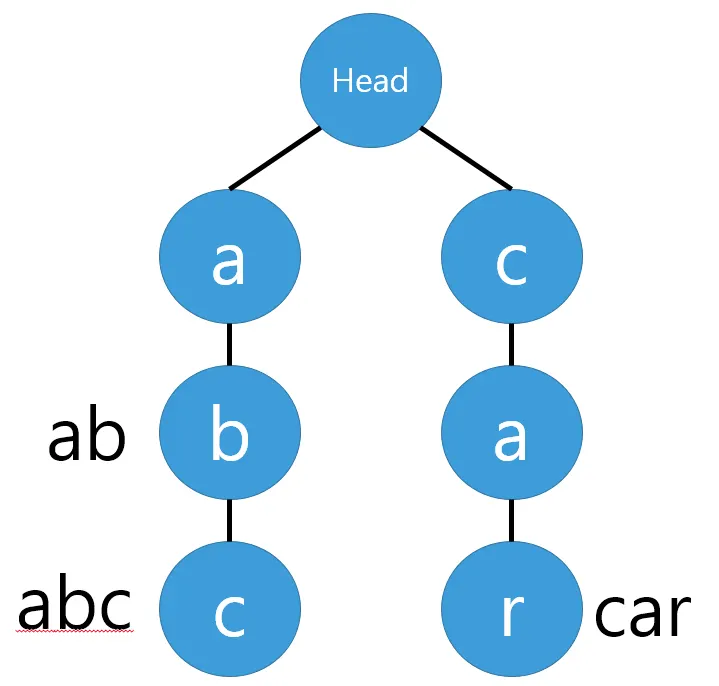
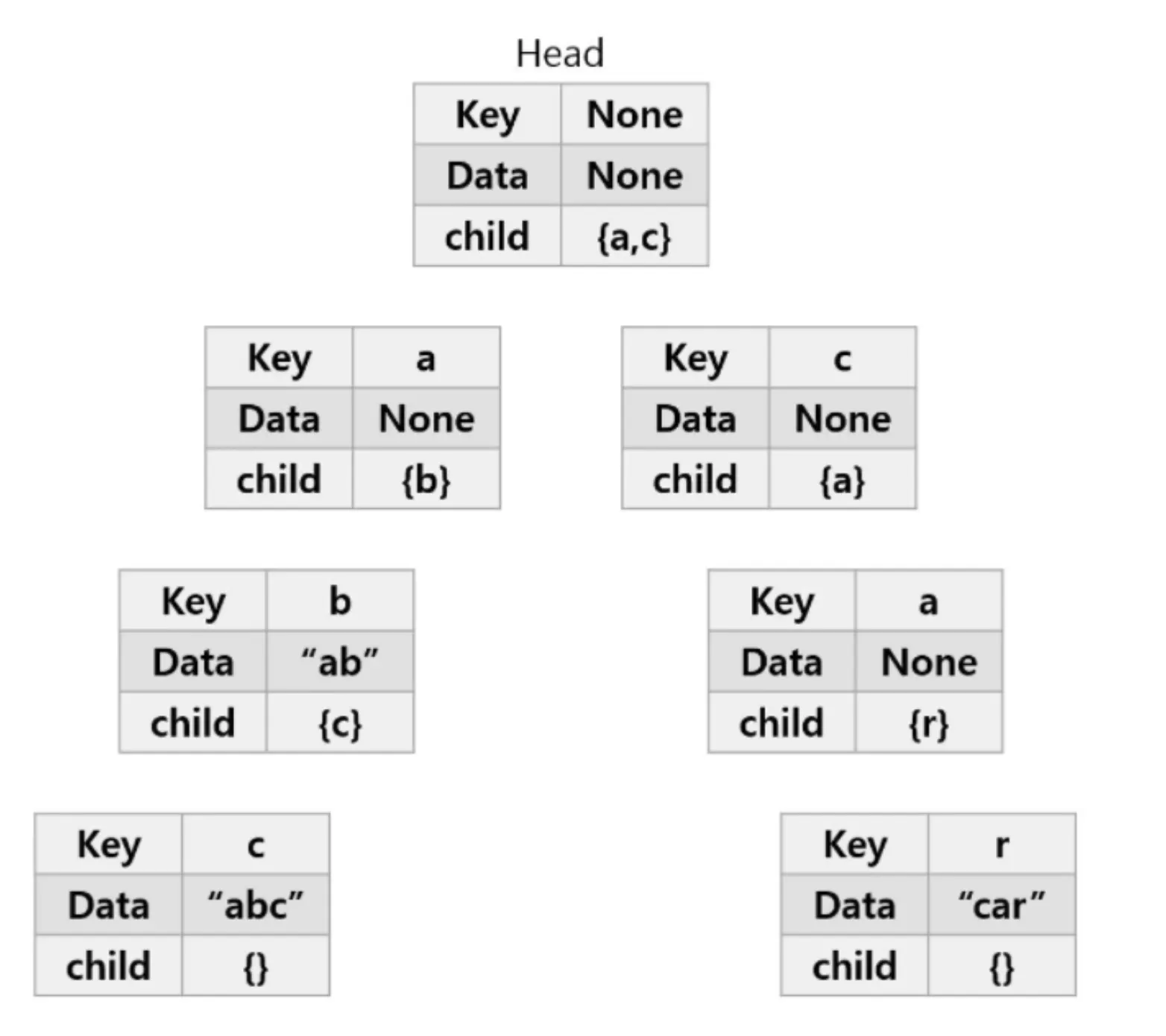
‘abc’, ‘ab’, ‘car’의 단어를 순서대로 트라이에 저장한다고 가정하자.
1.
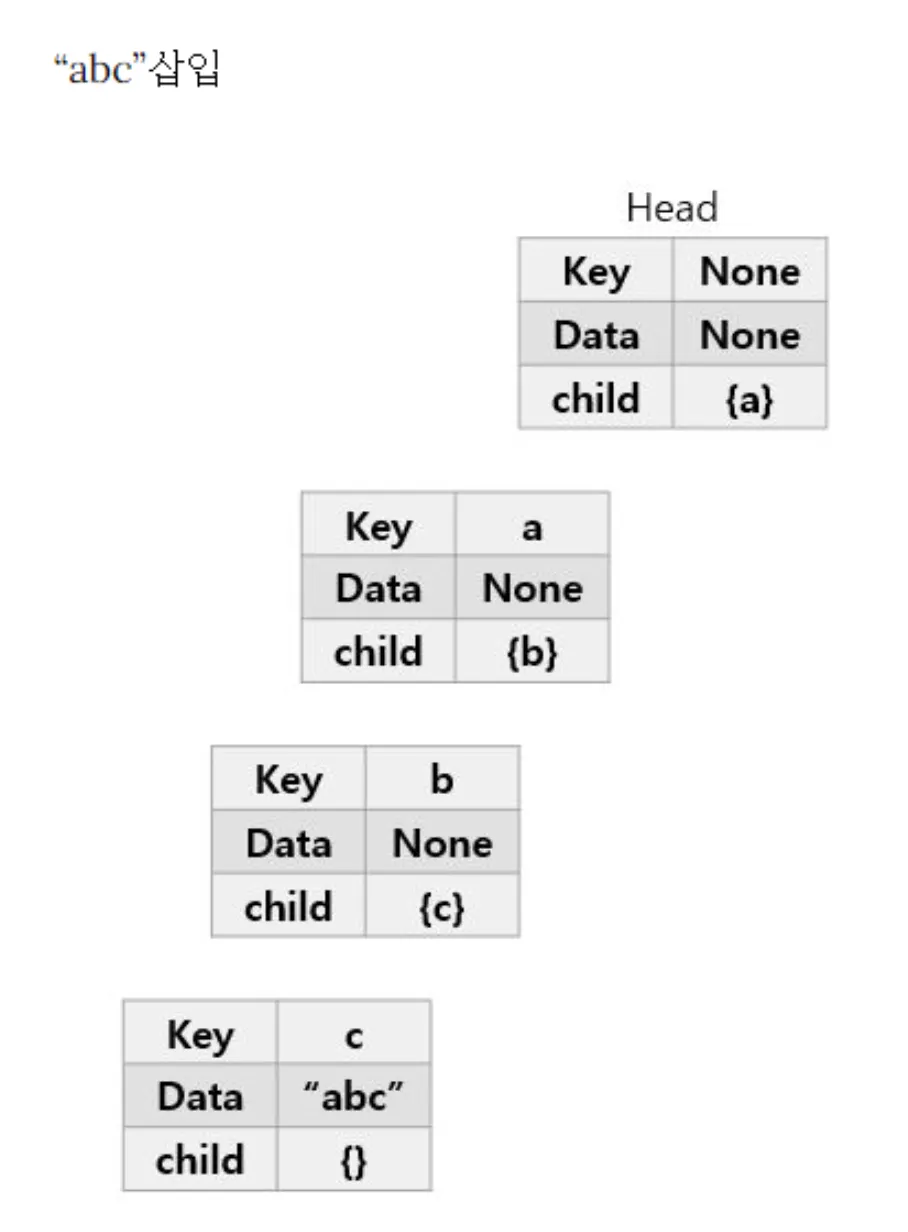
‘abc’를 트라이에 삽입한다.
a.
첫 번째 문자인 ‘a’부터 시작하자. 처음에는 트라이 자료구조에는 루트 노드를 제외하고 아무것도 없다. 그러므로 head의 자식 노드에 ‘a’를 추가한다.
b.
‘a’ 노드에도 자식이 하나도 없다. ‘a’ 의 자식 노드에 ‘b’를 추가한다.
c.
‘c’ 도 마찬가지로 ‘b’의 자식 노드로 추가한다.
d.
‘abc’ 단어가 여기서 끝남을 알리기 위해 ‘c’ 노드에 ‘abc’ 라고 데이터를 추가한다.
2.
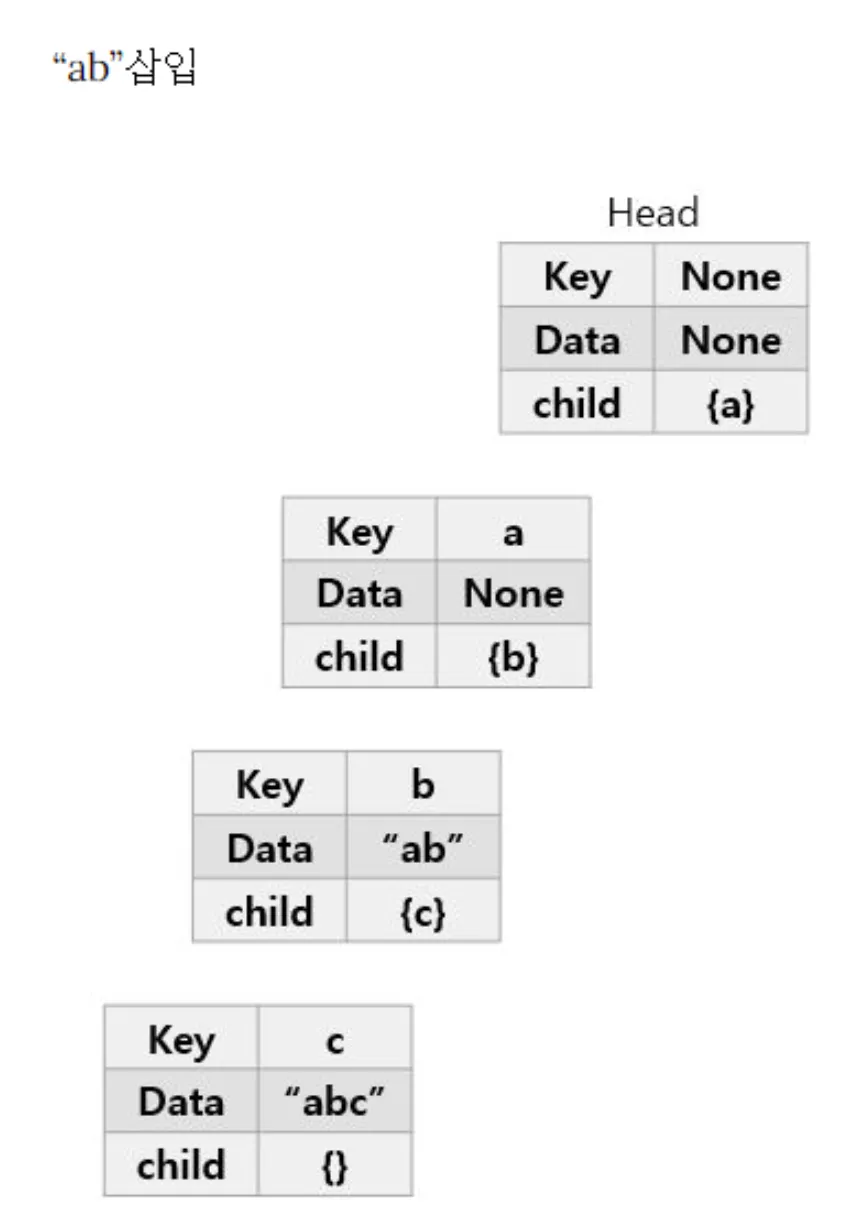
‘ab’ 를 트라이에 삽입한다.
a.
루트 노드의 자식 노드로 이미 ‘a’가 있다. 따라서 ‘a’를 추가하지 않고, 존재하는 ‘a’ 노드로 이동한다.
b.
‘b’도 ‘a’의 자식 노드로 이미 존재하므로 ‘b’ 노드로 이동한다.
c.
‘ab’ 단어가 여기서 끝이므로 ‘b’ 노드에 ‘ab’를 표시한다.
3.
‘car’ 를 트라이에 삽입한다.
a.
루트 노드의 자식 노드인 ‘c’가 존재하지 않는다. 따라서 ‘c’를 자식 노드로 추가한다.
b.
‘c’의 자식 노드에 ‘a’가 없다. 따라서 ‘a’를 자식 노드로 추가한다.
c.
‘a’의 자식 노드에 ‘r’이 없다. 따라서 ‘r’를 ‘a’의 자식 노드로 추가한다.
d.
‘car’ 단어가 여기서 끝나므로, ‘r’ 노드에 ‘car’를 표시한다.
CODE GIT REPO
git@github.com:044apde/My_algorithm.git
JavaScript
복사
코드 (임시 완성본)
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#define ALPHABET_SIZE 26
#define NAME_SIZE 50
#define TRUE 1
typedef struct s_trienode
{
struct s_trienode *child[ALPHABET_SIZE];
char string[NAME_SIZE];
} trienode;
typedef struct s_trietree
{
trienode *root;
} trietree;
trienode *create_node(void)
{
trienode *node = (trienode *)malloc(sizeof(trienode));
node->string[0] = '\0';
for (int i = 0; i < ALPHABET_SIZE; i++)
node->child[i] = NULL;
return (node);
}
int char_to_index(char c)
{
return (c - 'a');
}
void insert(trienode *root, const char *key)
{
trienode *current;
int index;
current = root;
for (int i = 0; i < (int)strlen(key); i++)
{
index = char_to_index(key[i]);
if (current->child[index] == NULL)
current->child[index] = create_node();
current = current->child[index];
}
for (int i = 0; i <= (int)strlen(key); i++)
current->string[i] = key[i];
printf("Inserting done: '%s'\n", key);
}
trienode *search(trienode *root, const char *key)
{
trienode *current;
int index;
current = root;
for (int i = 0; i < (int)strlen(key); i++)
{
index = char_to_index(key[i]);
if (current->child[index] != NULL)
current = current->child[index];
else
{
printf("OOPS.. there is no word started with '%s'\n", key);
return (NULL);
}
}
if (current->string[0] != '\0')
return (current);
for (int i = 0; i < ALPHABET_SIZE; i++)
{
if (current->child[i] != NULL)
{
current = current->child[i];
if (current->string[0] != '\0')
return (current);
i = 0;
}
}
return (NULL);
}
void delete(trienode *node, trietree *tree)
{
if (node == NULL)
return ;
for (int i = 0; i < ALPHABET_SIZE; i++)
delete(node->child[i], tree);
if (node != tree->root)
free(node);
}
void init_tiretree(trietree *tree)
{
tree->root = create_node();
return ;
}
int select_number(void)
{
int value;
printf("1. Insert string\n");
printf("2. Search string\n");
printf("3. Clean data\n");
printf("4. EXIT\n\n");
printf("Select number: ");
scanf("%d", &value);
return (value);
}
void insert_string(trienode *root)
{
char input[NAME_SIZE];
printf("insert string: ");
scanf("%s", input);
insert(root, input);
return ;
}
void search_string(trienode *root)
{
char input[NAME_SIZE];
trienode *search_result;
printf("insert string: ");
scanf("%s", input);
search_result = search(root, input);
if (search_result == NULL)
printf("There is no word start with '%s'\n", input);
else
printf("I think you want this: %s\n", search_result->string);
return ;
}
void clean_data(trienode *root, trietree *tree)
{
delete(root, tree);
printf("Clean done\n");
}
void quit_program(trienode *root, trietree *tree)
{
clean_data(root, tree);
printf("EXIT DONE...\n");
exit(0);
}
int main(void)
{
int input;
trietree tree;
init_tiretree(&tree);
printf("TRIE STARTED..\n");
while (TRUE)
{
input = select_number();
if (input == 1)
insert_string(tree.root);
else if (input == 2)
search_string(tree.root);
else if (input == 3)
clean_data(tree.root, &tree);
else if (input == 4)
quit_program(tree.root, &tree);
printf("=== === === === === === ===\n\n");
}
return (0);
}
JavaScript
복사
AVL tree 구현
이진탐색트리
이진탐색트리는 자기를 기준으로 작은 값은 왼쪽 자식 노드로 큰 값은 오른쪽 자식 노드로 보내는 트리를 말합니다.
이진탐색트리의 단점
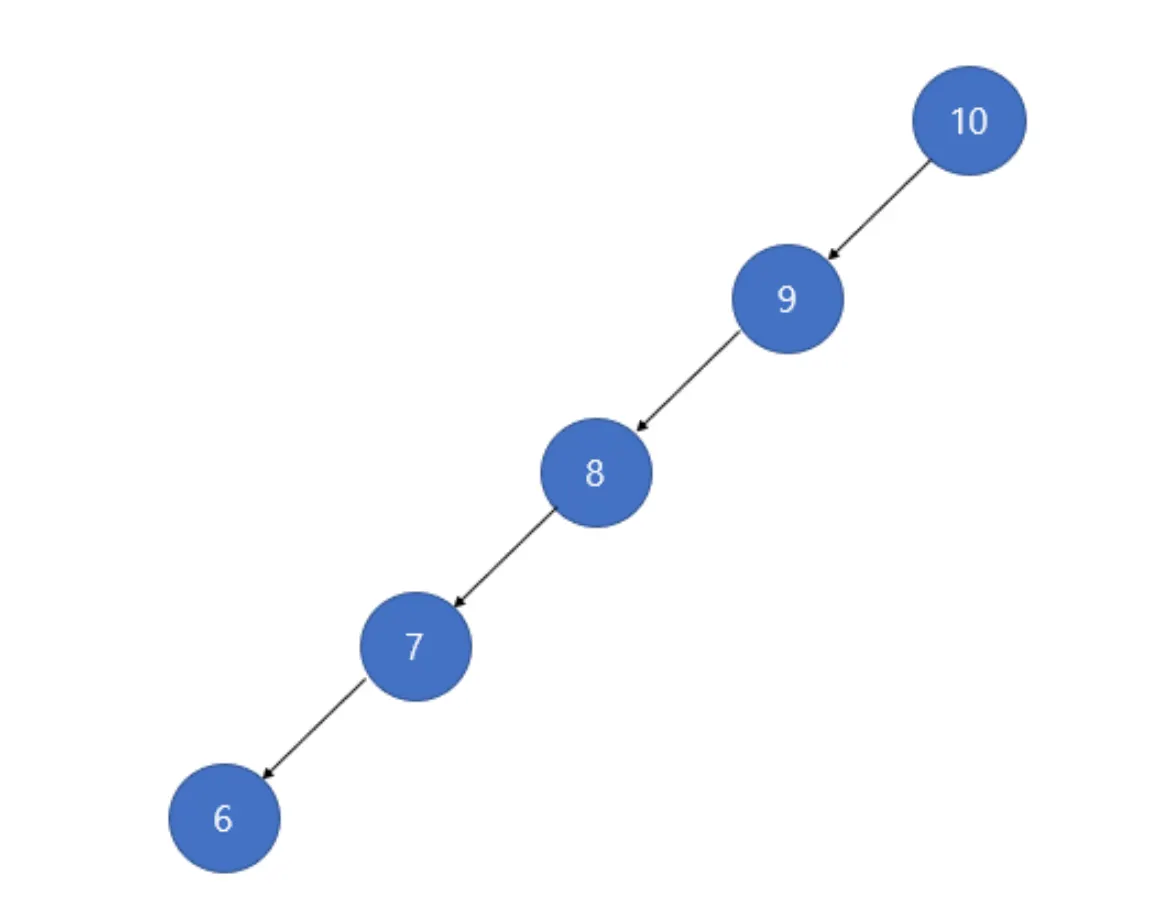
이진탐색트리의 탐색 시간은 O(logN)이지만, 최악의 경우에는 (노드가 한쪽으로 편향되어 있을 경우) O(N)입니다. 이러한 탐색 트리의 단점을 보안하기 위해서는 편향성을 보정해야 합니다. 이를 방법론적으로 만든 것이 바로 자가균형이진탐색트리입니다.
AVL tree
AVL tree는 위에서 말한 것처럼 이진탐색트리의 편향성을 해결하기 위해 고안된 방법입니다. 노드가 새로 들어올 때마다 재귀적으로 리프부터 루트까지 하나씩 balance factor를 검사합니다. 만약 이 때 BF의 절댓값이 1을 넘는다면 해당 노드를 기준으로 그 서브트리를 회전시킵니다. 이런 방식으로 리프부터 루트까지 검사하며 필요한 경우 로테이트를 해 균형을 맞춰주는 것이 AVL tree입니다.
Node
각 노드는 다음과 같은 구조체로 만들어져있습니다. height는 노드의 평향성을 확인하기 위한 수치입니다. 각 노드에서 왼쪽 서브트리의 높이와 오른쪽 서브트리의 높이를 뺀 값을 확인해 그 값이 -1 보다 작거나 +1 보다 크다면 균형을 맞추기 위해 트리를 조정해야 합니다. 이 때 각 서브트리의 높이를 확인하기 위한 수치인 height를 각 서브트리의 루트에 놓는 것입니다.
typedef sturct s_node
{
int data;
int heght; // 내 부모 노드가 내가 속한 서브트리의 깊이를 측정했을 때의 최대 값.
struct t_node *left;
struct t_node *right;
} t_node;
C
복사
height
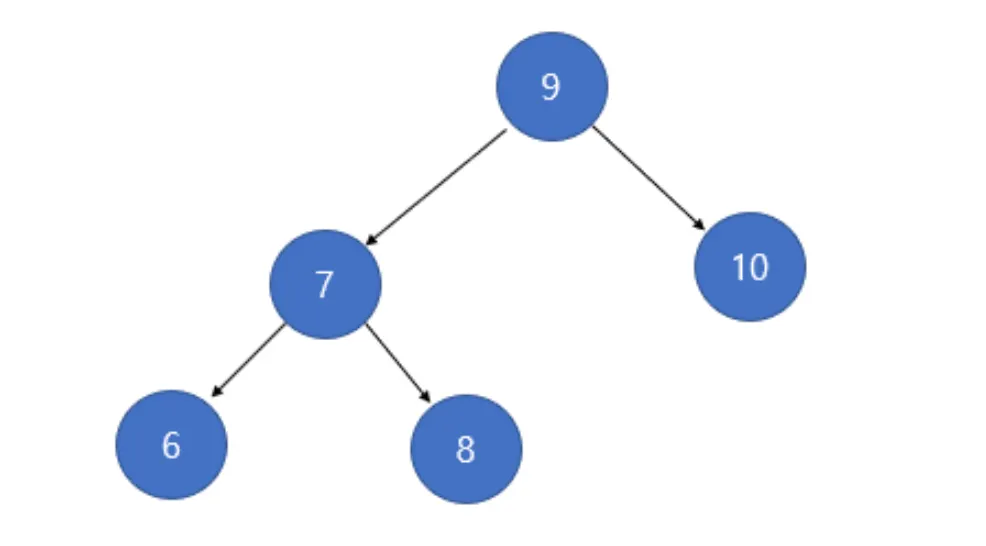
height는 위에서 말했듯이, BF(balance factor)를 확인하기 위한 자료입니다. 노드 9를 기준으로 왼쪽 서브트리의 높이는 2, 오른쪽 서브트리의 길이는 1입니다. 그리고 각 수치를 각 서브트리의 루트에 저장합니다. 그렇기 때문에 노드 7에는 2, 노드 10에는 1이 저장되어야 합니다. 이를 통해 알 수 있는 것은 각 노드는 최초 생성시 무조건 height 값이 1로 초기화되며, 자신의 오른쪽 서브트리외 왼쪽 서브트리 중 가장 height가 큰 것이 자신의 height값이 됩니다.
t_node* create_node(int value)
{
t_node* new_node = (t_node*)malloc(sizeof(t_node));
new_node->value = value;
new_node->left = NULL;
new_node->right = NULL;
new_node->height = 1;
return new_node;
}
void update_height(t_node* node)
{
node->height = 1 + max(height(node->left), height(node->right));
}
C
복사
rotate operation
나(노드)를 기준으르 현재 서브트리릐 높이 차이가 1을 초과한다면 트리의 높이를 재조정해야 합니다. 재조정 단계에서 행하는 기본 오퍼레이션은 2가지 입니다. 오른쪽으로 돌리거나, 아니면 왼쪽으로 돌리거나. 각 방법에 대해 배워봅시다.
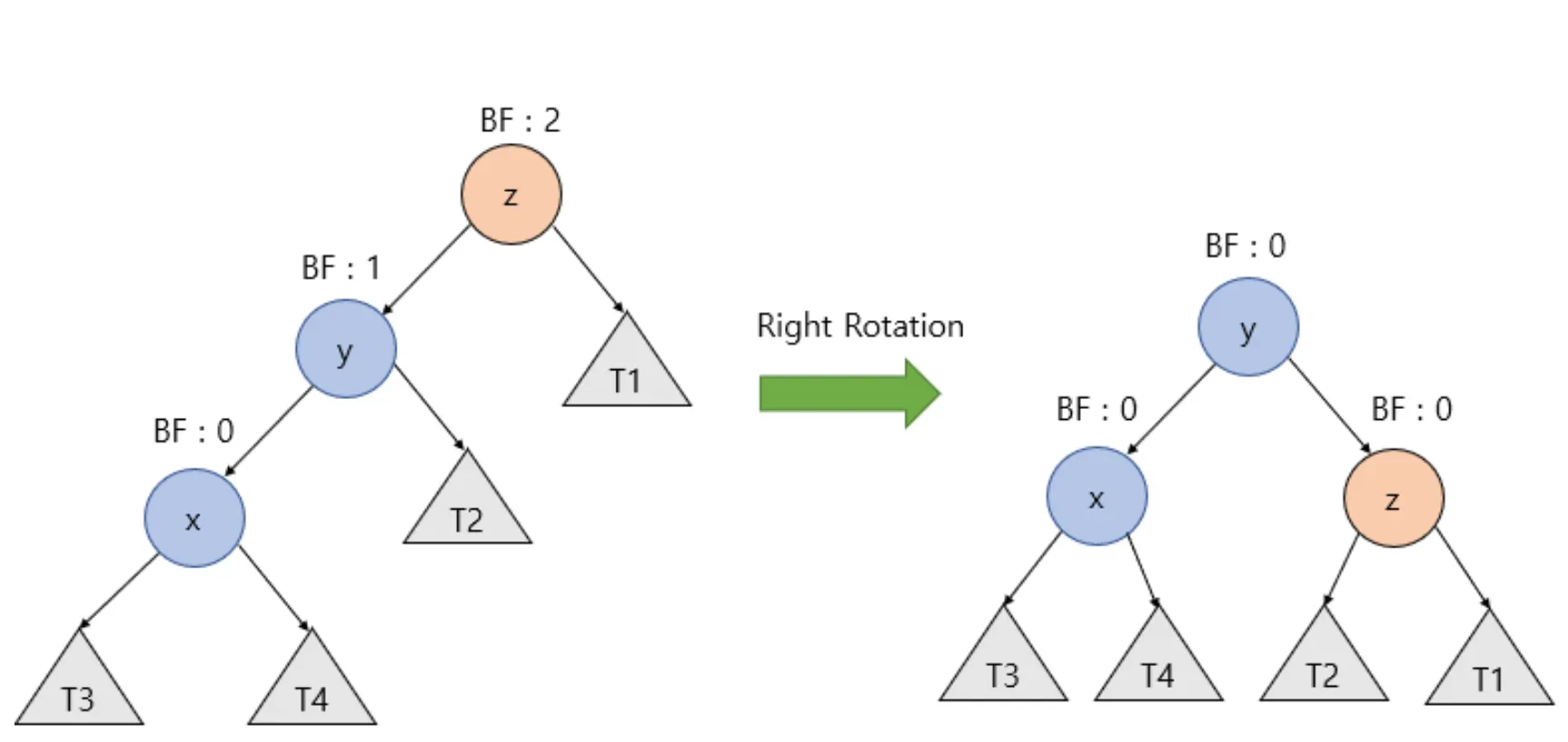
rotate right
나를 기준으로 노드가 좌-좌로 편향되어 있을 때 오른쪽으로 돌립니다. 나(z), 좌(y), 좌-좌(x)라고 하면, 나(z)가 좌(y)의 오른쪽 자식으로 들어갑니다. 좌(y)가 오른쪽 자식이 있을 수 있으므로 이를 T2라고 하고 T2를 나(z)의 왼쪽 자식으로 지정합니다.
t_node* rotate_right(t_node* z)
{
t_node* y = z->left;
t_node* t2 = y->right;
y->right = z;
z->left = t2;
update_height(z);
update_height(y);
return y;
}
C
복사
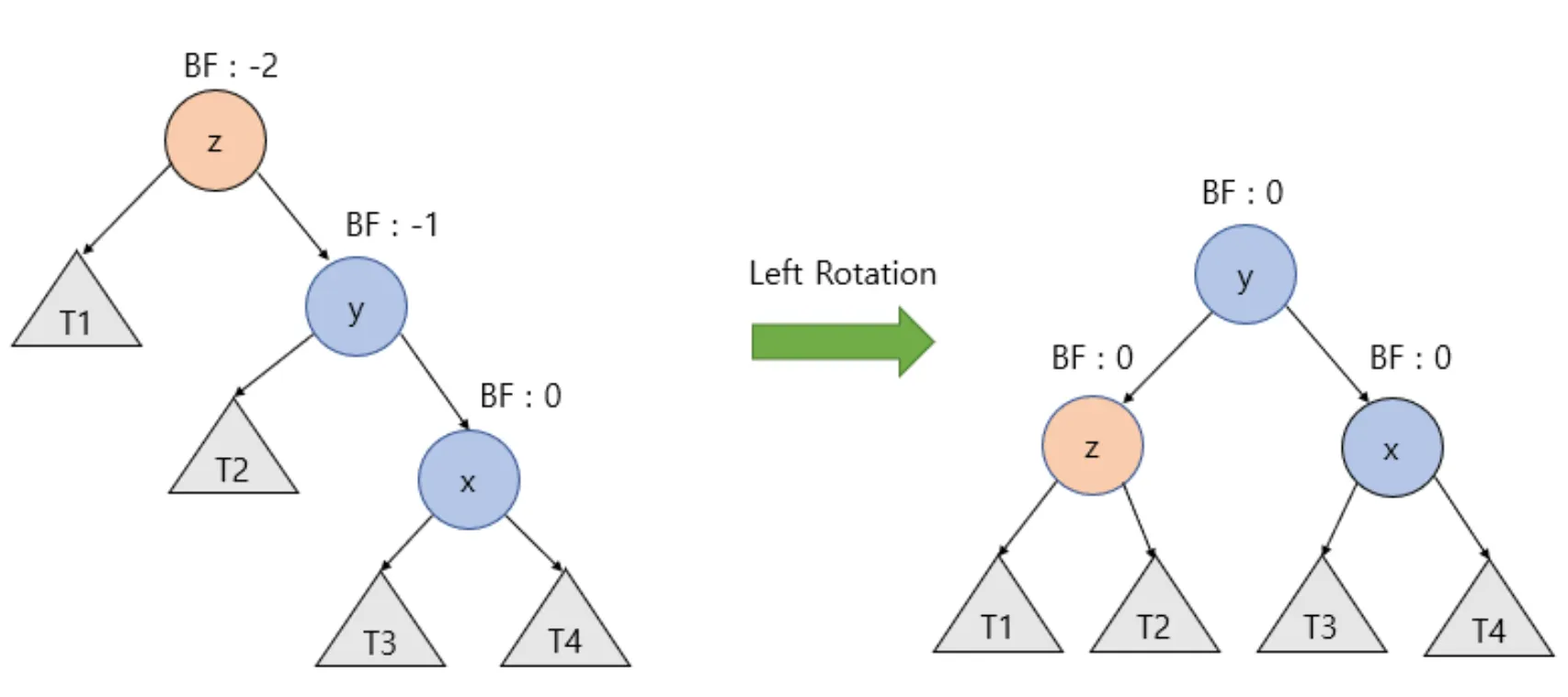
rotate left
나를 기준으로 노드가 우-우로 편향되어 있을 때 오른쪽으로 돌립니다. 나(z), 우(y), 우-우(x)라고 하면, 나(z)가 좌(y)의 왼쪽 자식으로 들어갑니다. 오ㅜ(y)가 왼쪽 자식이 있을 수 있으므로 이를 T2라고 하고 T2를 나(z)의 오른쪽 자식으로 지정합니다.
t_node* rotate_left(t_node* z)
{
t_node* y = z->right;
t_node* t2 = y->left;
y->left = z;
z->right = t2;
update_height(z);
update_height(y);
return y;
}
C
복사
insert
이제 기본 AVL tree의 기본 동작을 알았으니, 루트부터 노드를 push합시다. 노드를 삽입하면 루트노드 부터 시작해 내려가며 값을 비교합니다. 각 노드와 값을 비교해 노드보다 작다면 그 노드의 왼쪽 자식으로, 크다면 오른쪽 자식으로 내려갑니다. 단계적으로 내려가면서 자식의 노드가 비어있을 때 까지 내려갑니다. 이 때 insert 함수는 재귀적으로 동작하는데, 노드를 리프에 삽입한 후 스택에 쌓인 함수들이 종료되면서 노드를 타고 루트까지 올라갑니다. 루트까지 올라가면서 각 노드의 BF를 검사하고 BF에 문제가 있다면 rotate를 진행합니다.
t_node* insert(t_node* node, int value)
{
int balance;
if (node == NULL)
return (create_node(value));
if (value < node->value)
node->left = insert(node->left, value);
else if (value > node->value)
node->right = insert(node->right, value);
else
return node;
update_height(node);
balance = height(node->left) - height(node->right);
if (balance > 1)
{
if (value < node->left->value)
return rotate_right(node);
else
{
node->left = rotate_left(node->left);
return rotate_right(node);
}
}
else if (balance < -1)
{
if (value > node->right->value)
return rotate_left(node);
else
{
node->right = rotate_right(node->right);
return rotate_left(node);
}
}
return node;
}
C
복사
The code
다음은 전체 코드입니다.
#include <stdio.h>
#include <stdlib.h>
#define TRUE 1
#define FALSE 0
typedef struct node
{
int value;
int height;
struct node* left;
struct node* right;
} t_node;
int height(t_node* node)
{
if (node == NULL)
return 0;
return node->height;
}
int max(int a, int b)
{
if (a > b)
return a;
return b;
}
t_node* create_node(int value)
{
t_node* new_node = (t_node*)malloc(sizeof(t_node));
new_node->value = value;
new_node->left = NULL;
new_node->right = NULL;
new_node->height = 1;
return new_node;
}
void update_height(t_node* node)
{
node->height = 1 + max(height(node->left), height(node->right));
}
t_node* rotate_right(t_node* z)
{
t_node* y = z->left;
t_node* t2 = y->right;
y->right = z;
z->left = t2;
update_height(z);
update_height(y);
return y;
}
t_node* rotate_left(t_node* z)
{
t_node* y = z->right;
t_node* t2 = y->left;
y->left = z;
z->right = t2;
update_height(z);
update_height(y);
return y;
}
t_node* insert(t_node* node, int value)
{
int balance;
if (node == NULL)
return (create_node(value));
if (value < node->value)
node->left = insert(node->left, value);
else if (value > node->value)
node->right = insert(node->right, value);
else
return node;
update_height(node);
balance = height(node->left) - height(node->right);
if (balance > 1)
{
if (value < node->left->value)
return rotate_right(node);
else
{
node->left = rotate_left(node->left);
return rotate_right(node);
}
}
else if (balance < -1)
{
if (value > node->right->value)
return rotate_left(node);
else
{
node->right = rotate_right(node->right);
return rotate_left(node);
}
}
return node;
}
int main()
{
t_node* root = NULL;
root = insert(root, 10);
root = insert(root, 20);
root = insert(root, 30);
root = insert(root, 40);
root = insert(root, 35);
printf("root:%d\n", root->value);
printf("root->left:%d\n", root->left->value);
printf("root->right: %d\n", root->right->value);
printf("root->right->left: %d\n", root->right->left->value);
printf("root->right->right: %d\n", root->right->right->value);
return 0;
}
JavaScript
복사
Q & A
•
트리가 효율적이라는 것이 구체적으로 어느 부분인지? 어떤 용도로 쓰는지?
◦
file system에서 쓴다
◦
오름차순, 내림차순, 데이터 탐색 시 또는 BFS/DFS 최대/최솟값 검색시 효율이 높다
•
부모노드가 없는 노드 = ROOT 라고 생각해도 되나?
◦
OF COURSE 이다.
•
자식노드가 없는 노드는 모두 LEAF 인가?
◦
이또한 OF COURSE 이다.
•
정 이진트리와 완전 이진트리의 차이점이 뭔지?
◦
정 이진트리는 자식트리로 빠짐없이 꽉 차있어야 함. 하나라도 지워지는 순간 완전 이진트리가 된다.
•
트리의 종류가 많은데 종류를 유지해야하나? 종류를 나누는 이유는 무엇인가?
◦
목적에 따라(혹은 문제 해결방식에 따라) 트리를 만들다보니 여러 유형의 트리가 생겨서 많이 보이는 특정 유형에 이름을 붙인 것으로 알고있다.
•
Heap = 우선순위 큐 인가요?
◦
우선순위 Queue를 가장 효율적으로 구현하는 방식이 Heap으로 구현하는 것이라고 생각합니다.
•
Heap도 트리인가요?
◦
완전이진트리를 만족하는 트리의 한 종류라고 할 수 있습니다.
•
선형 데이터구조는 왜 계층이 없다고 하신건가요?
◦
부모-자식 관계 없이 순서만 존재한다. 억지로 구현한다고 해도 편향될 가능성이 높아진다.
마무리
이 문서를 정리한 사람: shikim