CPP 모듈 과제중에 삼각형 내부의 점을 판단하는
다음과 같은 삼각형이 있다고 생각해봅시다.
삼각형 내부의 점을 하나의 집합으로 표현하고자 합니다.
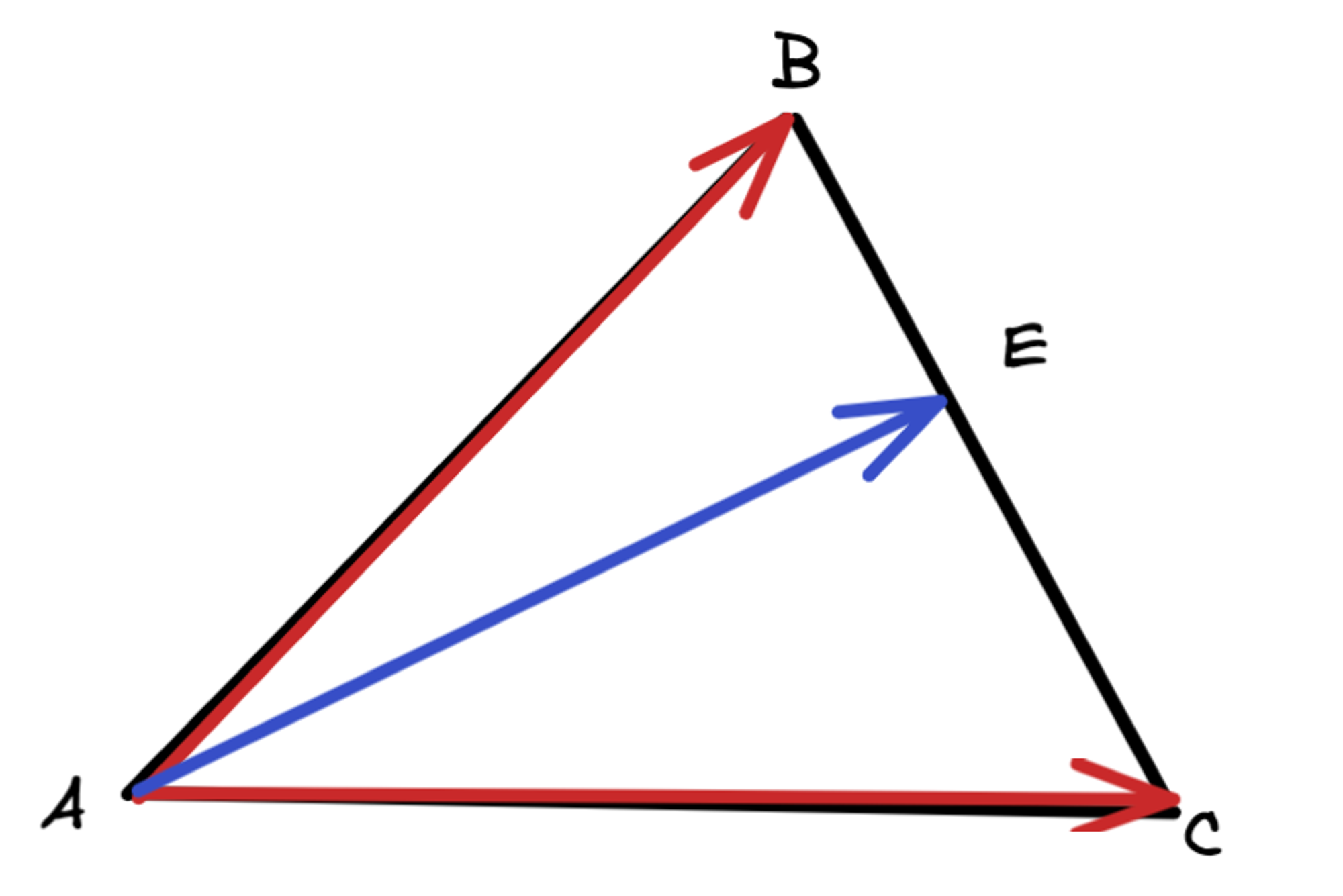
우선 AB, AC의 벡터가 있다고 생각해봅시다.
다음 그림처럼 벡터 AB와 AC가 있다고 생각해봅시다. 그리고 BC사이의 임의의 점 E가 있다고 생각을 해봅시다.
그러면 E는 다음과같이 표현이 가능합니다.
다음과 같이 나타낼 수 있습니다. 저말이 무슨말 이냐면 t를 0에서 1사이에 어떤값을 넣더라도 AE에서 E는 BC상의 점 위에 있다는것을 나타냅니다. 여기서 AE의 크기를 0에서 1까지 조절하면 삼각형 내부의 점으로 표현 할 수 있습니다.
alpha와 t를 각각 0과 1사이로 조정을 하면서 삼각형 내부의 모든점으로 표현할 수 있습니다.
즉
alpha와 t가 조건에 맞기만하면 그점은 무조건 삼각형 내부에 있는 점입니다.
그럼 임의의 점이 들어가는지 어떻게 알아 낼 수 있냐.?
우리가 생각하는 어떤점도 위의 식으로 바꿀 수 있습니다. 어떤점을 위처럼 2개의 벡터로 변경한뒤 위의 삼각형 조건에 만족하는지만 확인하면 가능합니다.
제가 설명한 방법만 정답인것도 아니고 가장 쉬운방법도 아닐거라고 생각합니다. 과제를 하신분들은 이런방법도 있었구나 아직 안하신분들은 읽어 보시면 도움이 될꺼라 생각합니다.
그럼 만족을 실제로 계산을 하는방법은 다음에 설명을 하도록 하겠습니다.