목차
트리(tree)란 무엇인가?
출처 : Monsieur_Songsong
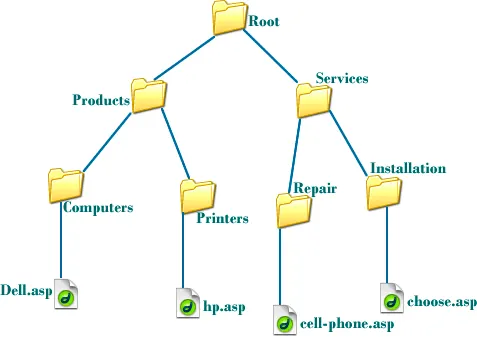
트리 구조는 비선형(Non-linear) 자료구조 중 하나이다. 비선형 자료구조에서는 하나의 자료 뒤에 여러 개의 자료가 존재할 수 있기 때문에 폴더 구조와 같은 계층적 구조를 나타내기에 적절하다.
트리 용어 정리
출처 : Velog
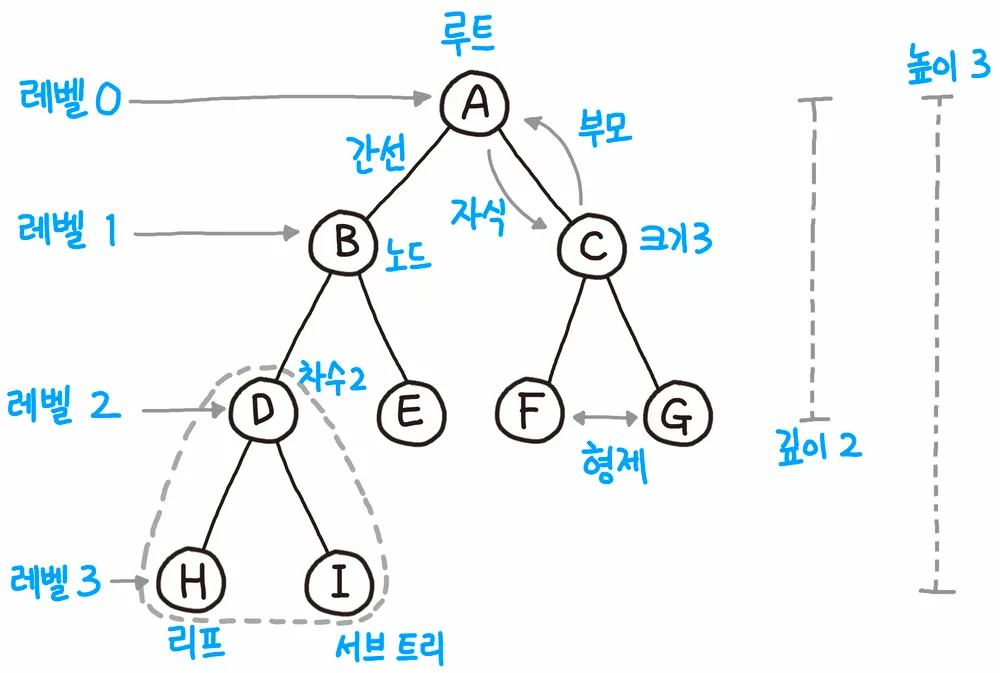
주로 사용하는 용어는 다음과 같다.
용어 | 의미 |
노드(node) | 동그라미 |
간선(edge) | 노드와 노드를 이어주는 선 |
레벨(level) | 트리의 특정 깊이를 가지는 노드의 집합 |
루트 노드(root node) | 트리의 가장 높은 곳에 위치한 노드 |
단말 노드(leaf node) | 자식이 없는 노드 |
형제 (sibling) | 같은 부모 노드를 가진 노드 |
•
노드의 깊이(depth) : 루트에서 어떤 노드에 도달하기 위해 거쳐야 하는 간선의 수
◦
D 의 깊이 : 2
◦
H 의 깊이 : 3
•
노드의 레벨(level) : 트리의 특정 깊이를 가지는 노드의 집합. 0 또는 1부터 시작한다.
◦
A 의 레벨 : 0
◦
B, C 의 레벨 : 1
•
트리의 높이(height) : 루트 노드에서 가장 깊숙히 있는 노드의 깊이
◦
3
이진 트리(binary tree)
이진 트리란 모든 노드의 자식 노드가 최대 2개의 노드를 가지는 트리를 의미한다.
이진 트리의 종류
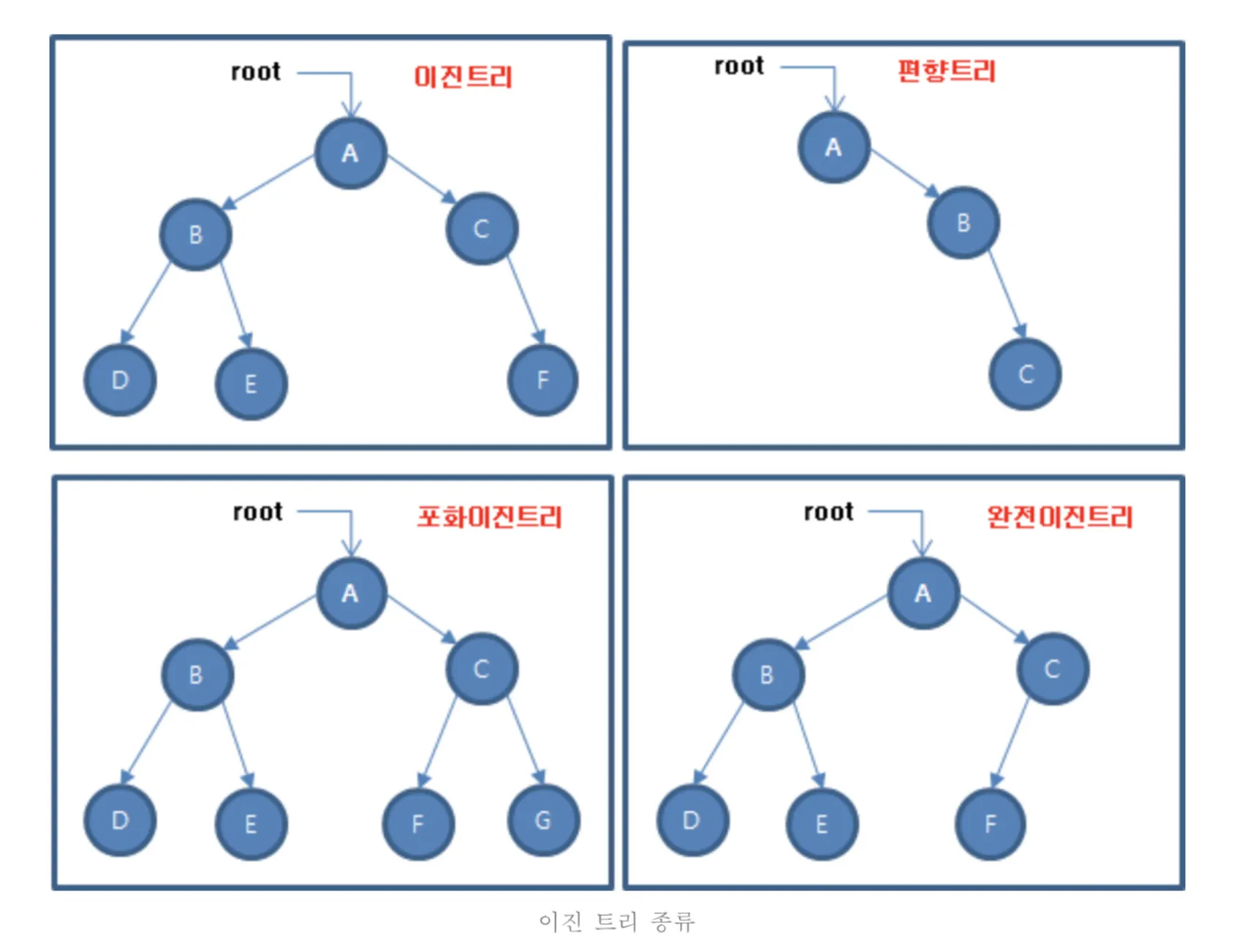
이진 트리는 아래의 그림처럼 형태에 따라 세부적으로 다르게 부르고 있지만, 결국 모두 이진 트리이다.
출처 : github.io
•
포화 이진 트리(full binary tree)
◦
모든 레벨에서 노드들이 모두 채워진 트리
•
완전 이진 트리(complete binary tree)
◦
마지막 레벨을 제외하고 노드가 모두 채워진 트리. 마지막 레벨도 다 채워져 있을 수도 있다.
•
편향 트리(Skewed binary tree)
◦
왼쪽 또는 오른쪽 서브트리만 가지는 트리
◦
최악의 경우에는 모든 노드를 탐색해야 하므로 시간 복잡도는 이 된다.
◦
이처럼 균형이 깨진 트리에서 스스로 균형을 잡고 시간 복잡도를 을 보장하기 위해 “레드 블랙 트리"나 “AVL 트리”를 사용한다.
이진 트리를 사용하는 이유?
선형 구조와 달리 탐색과 삽입에서 연산 횟수를 대폭 줄일 수 있기 때문이다.
배열, 연결 리스트, 스택, 큐, 데크(Deque)와 같은 선형 자료구조에서는 하나의 자료 뒤에 오직 하나의 자료만 존재한다. 그렇기 때문에 선형 자료구조에서는 정렬이 되어있지 않은 상태에서 특정 값을 탐색할 때, 최악의 시간 복잡도는 맨 끝까지 탐색하는 경우이기 때문에 이 된다.
하지만, 이진 트리에서는 탐색하는데 최적의 시간 복잡도는 이 된다. 이를 증명하면 다음과 같다.
포화 이진 트리의 루트 노드의 depth 를 0 으로 지정했을 때, 노드(데이터) 개수는 다음과 같다. n 은 데이터의 개수이고, h 는 트리의 높이를 의미한다.
위의 수식에서 h 를 n 에 관한 식으로 바꾸면 다음과 같다.
여기에 시간 복잡도를 적용하면 다음과 같다.
순회 종류
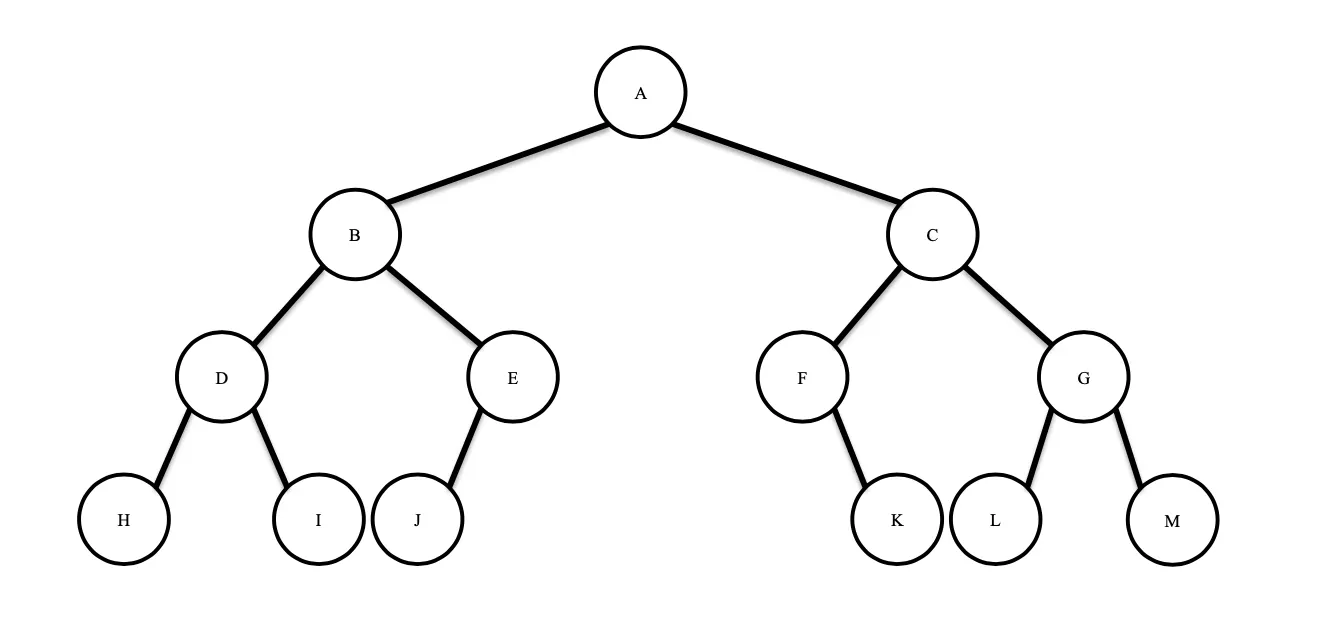
위와 같은 이진 트리가 있을 때, 대표적인 순회 3가지와 순회 결과는 다음과 같다.
구분 | 순서 | 순회 결과 |
전위 순회 (pre-order) | 가운데 → 왼쪽 → 오른쪽 | A B D H I E J C F K G L M |
중위 순회 (in-order) | 왼쪽 → 가운데 → 오른쪽 | H D I B J E A F K C L G M |
후위 순회 (post-order) | 왼쪽 → 오른쪽 → 가운데 | H I D J E B K F L M G C A |
순회를 코드로 구현하기 (C언어)
트리 구조에서 순회를 할 때는 “재귀"적으로 구현하는 것이 쉽다. 반복문으로도 구현할 수 있지만, 다소 복잡하기에 아래의 예제에서는 연결 리스트를 이용하여 트리를 구현했다.
코드의 흐름은 크게 다음과 같이 진행된다.
•
노드의 왼쪽 자식이 존재하는가?
◦
YES → 재귀 함수 호출(왼쪽 자식)
•
노드의 오른쪽 자식이 존재하는가?
◦
YES → 재귀 함수 호출(오른쪽 자식)
위와 같이 진행하다가, 왼쪽 및 오른쪽 노드가 모두 없으면 함수 호출이 끝나서 다시 돌아온다.
순회에 사용한 재귀적 구조는 모두 같으며, 노드의 데이터를 출력하는 순서만 바꾸면 순회의 종류가 바뀐다.
전위 순회
// 전위 순회 (pre-order)
#include "bintree.h"
static void preOrderTraversalNode(BinTreeNode *pNode)
{
if (pNode == NULL)
return ;
printf("node data: %c\n", pNode->data);
if (pNode->pLeftChild != NULL)
preOrderTraversalNode(pNode->pLeftChild);
if (pNode->pRightChild != NULL)
preOrderTraversalNode(pNode->pRightChild);
}
void preOrderTraversal(BinTree *pBinTree)
{
if (pBinTree == NULL)
return ;
printf("✅ preorder traversal start\n");
preOrderTraversalNode(pBinTree->pRootNode);
}
C
복사
중위 순회
// 중위 순회 (in-order)
#include "bintree.h"
static void inOrderTraversalNode(BinTreeNode *pNode)
{
if (pNode == NULL)
return ;
if (pNode->pLeftChild != NULL)
inOrderTraversalNode(pNode->pLeftChild);
printf("node data: %c\n", pNode->data);
if (pNode->pRightChild != NULL)
inOrderTraversalNode(pNode->pRightChild);
}
void inOrderTraversal(BinTree *pBinTree)
{
if (pBinTree == NULL)
return ;
printf("✅ inorder traversal start\n");
inOrderTraversalNode(pBinTree->pRootNode);
}
C
복사
후위 순회
// 후위 순회 (post-order)
#include "bintree.h"
static void postOrderTraversalNode(BinTreeNode *pNode)
{
if (pNode == NULL)
return ;
if (pNode->pLeftChild != NULL)
postOrderTraversalNode(pNode->pLeftChild);
if (pNode->pRightChild != NULL)
postOrderTraversalNode(pNode->pRightChild);
printf("node data: %c\n", pNode->data);
}
void postOrderTraversal(BinTree *pBinTree)
{
if (pBinTree == NULL)
return ;
printf("✅ postorder traversal start\n");
postOrderTraversalNode(pBinTree->pRootNode);
}
C
복사
참고자료
•
선형(Linear) / 비선형(NonLinear) 자료구조 [github.io]
•
[Algorithm] 트리의 개념과 용어정리 [github.io]
•
이진트리 시간복잡도 [velog]
•
[자료구조] 트리(Tree)란 [github.io]
•
알고리즘 ) Red-Black Tree [티스토리]