목표
어떠한 데이터를 찾아내거나 저장할때는 어떤 위치에 데이터가 있는지 혹은 어떤 위치에 데이터를 저장할지가 상당히 중요하다. 그러한 위치에 따라서 검색의 속도나 저장의 속도가 현저히 차이가 나기 때문이다. 이러한 자료구조는 데이터베이스의 근간이기 때문에 개발자로서 이해하는게 중요하고 이러한 자료구조를 통해서 앞으로 프로그램을 설계해 나가는것도 중요하다. 따라서, 대표적인 3가지의 트리들을 선정했고 이 포스트에서 공유할 예정이다. 늘 그렇듯이 실제 코드가 궁금하다면 하단의 깃허브를 참조하면된다.
01 이진 검색 트리
본격적인 이진 검색트리에 대한 설명을 하기전에 왜? 이진 검색트리가 탄생 했는지 생각해보자. 우선 아무런 자료구조 없이 데이터베이스에 데이터를 저장했다고 생각해보자. 랜덤 엑세스가 불가능한 저장 장치에 데이터를 저장했다면, 당연히 우리는 앞에서 부터 차근히 하나하나씩 엑세스 한다음 비교하고 엑세스 한다음 비교하고를 반복해야할 운명이다. 그럼 검색에만 O(n)을 사용해야한다. 만약 모든 데이터 엑세스가 이렇다고 한다면 상당히 비효율적인 구조라고 생각이 든다. 선배 프로그래머들도 이러한 생각을 하지 않은것은 아니다. 이러한 문제의식은 자료구조의 발전으로 이어졌고 가장 단순한 이진 검색트리가 탄생하고 점차 진화해나갔다고 생각하면된다. 이진 검색 트리는 데이터 엑세스를 평균적을 O(logn)으로 만들어준다. 다만, 최악의 경우는 O(n)이다. 최악의 경우도 O(logn)으로 만드는 자료구조가 대표적으로 두개 있는데, AVL 트리와 레드 블랙 트리이다. 둘중에 우리는 대표적으로 레드 블랙 트리를 배워볼것이다.
01) 규칙
•
이진 검색 트리의 각 노드는 키 값을 하나씩 갖는다. 각 노드의 키 값은 모두 달라야 한다.
•
최상위 레벨에 루트 노드가 있고, 각 노드는 최대 두 개의 자식 노드를 갖는다.
•
임의의 노드의 키 값은 자신의 왼쪽에 있는 모든 노드의 키 값보다 크고, 오른쪽에 있는 모든 노드의 키 값보다 작다.
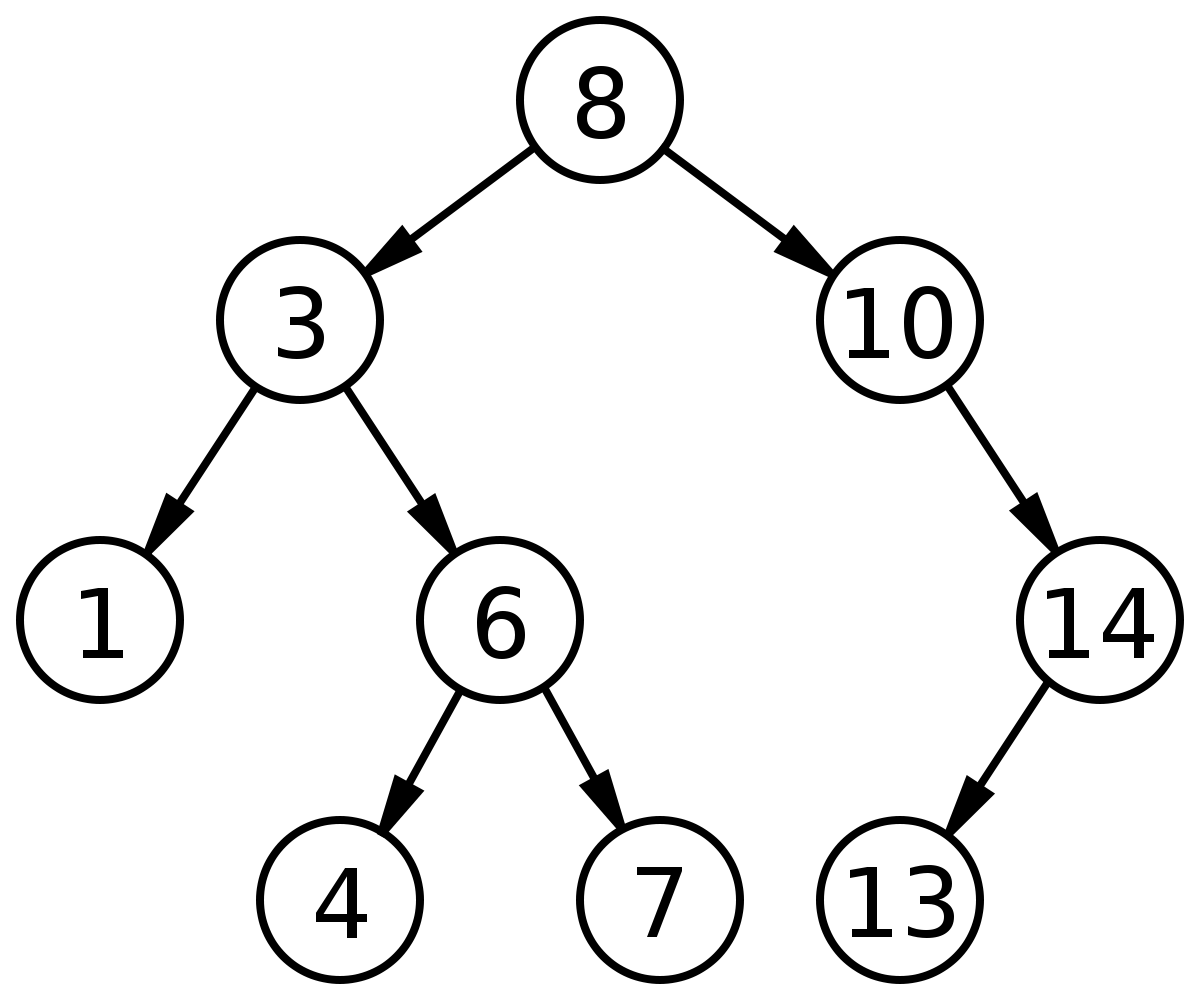
완벽한 예는 위의 사진으로 찾아볼 수 있다. 루트는 8이고 8보다 작은 노드들은 왼쪽 서브트리에 구성되고 8보다 큰 노드들은 오른쪽에 구성된다. 최대 두 개의 자식노드를 갖고 있고 전부 유니크한 키값을 가지고 있다.
02) 검색
treeSearch(t, x) // t -> root 노드, x 검색하고자 하는 키
{
if(t == null or key[t] == x) return t;
if (x < key[t])
return treeSearch(left[t], x);
else
return treeSearch(right[t], x);
}
Java
복사
위의 규칙을 만족하는 자료구조내에서 검색이 어떻게 이루어지는지 생각해보자. 위으 슈도코드를 생각해보면 전체적인 과정은 해당 노드(t)의 값과 찾고자하는 값(x)를 비교해서 왼쪽으로 갈지 오른쪽으로 갈지 생각한다. 예를 들자면 아래와 같다.
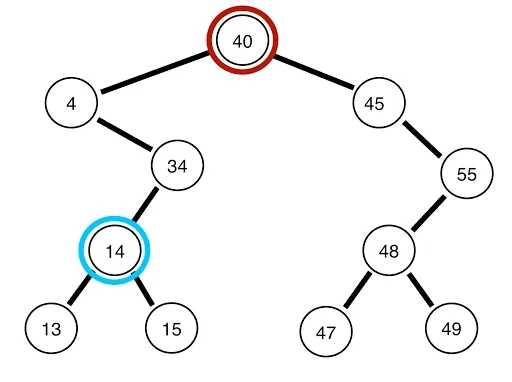
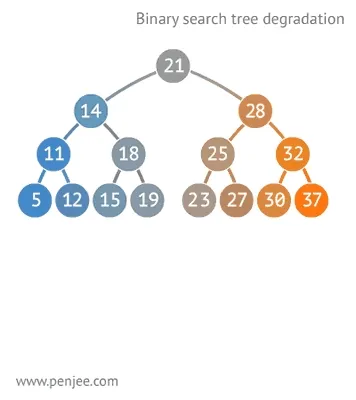
위의 구조에서 14를 찾고자 한다면 40보다 작기때문에 왼쪽으로 4보다 크기때문에 오른쪽으로 34보다 작기때문에 왼쪽으로 가서 마지막 비교를 하면 14가 나오고 해당 인덱스에 있는 자료를 찾아서 보낼 수 있다. 그렇다면 이 검색의 평균 시간복잡도는 어떻게 될까? 당연하게도 O(logn)이다. 왜냐하면, 균형잡힌 트리의 높이가 logn이다. 3층짜리 트리는 7개의 데이터를 저장할 수 있다(log7). 층수가 높아 질수록 logn으로 점근된다. 하지만, 트리의 높이가 n이 될 수도 있다.
이렇게 일자로 쭈욱 펼쳐진 자료구조 또한, 이진 검색 트리의 모든 규칙을 만족하게된다. 따라서, 이러한 자료구조에서는 O(n)이 걸리게 된다.
03) 삽입
treeInsert(t, x) // t -> root 노드, x 넣고자 하는 키
{
if(t == null)
{
key[r] = x; // r -> 신규 노드
left[r] = null;
right[r] = null;
return r;
}
if (x < key[t])
{
left[t] = treeInsert(left[t], x);
return t;
}
else
{
right[t] = treeInsert(right[t], x);
return t;
}
}
Java
복사
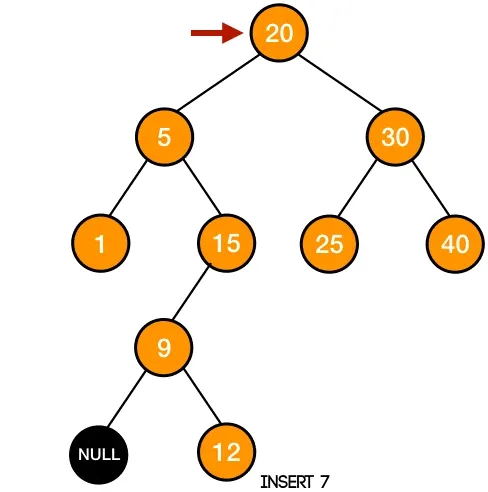
슈도코드를 생각해보면 서치를 계속해서 규칙에 맞고 null인 노드를 찾아서 그곳에 집어넣는다. 또, 찾은 곳에 오른쪽이 되었던 왼쪽이 되었든 붙여 넣는다. 재귀의 끝에서는 신규 노드가 리턴되고 그 밑으로는 계속해서 재귀가 들어갔던 노드가 리턴되어서 재귀로 계속 재할당 되고 있다. 재할당을 막기위해서 루프로 구현 할 수도 있지만, 코드가 복잡해져서 오히려 좋지 않다.
위의 움짤을 보면 직관적으로 코드를 이해 할 수 있다. 시간복잡도는 검색과 똑같다.
04)삭제
delete(t, r) // t: 트리의 루트 노드, r: 삭제하고자 하는 노드
{
if(r이 리프노드(자식이 없는 노드))
그냥 r을 삭제한다.
else if (r의 자식이 하나만 있음)
해당 자식을 r의 자리로 넣고 r을 삭제한다.
else{ // 자식이 두개인 경우
r의 오른쪽 서브트리의 최소 원소 노드(s)를 찾는다. // 왼쪽 서브트리의 최대값도 이용가능하다.
r을 s로 대체한 후에 r을 삭제한다.
}
}
Java
복사
삭제의 경우에는 삭제할 해당 노드를 찾은 후에 세가지 경우로 나뉜다. 자식 노드가 없는 경우 1), 자식 노드가 한개인 경우 2), 자식 노드가 두개인 경우 3). 1, 2 번의 경우는 간단하게 해결 할 수 있다. 그냥 삭제하거나 한개뿐인 자식을 해당노드로 대체하고 해당 노드를 삭제하면된다. 문제는 자식이 두개인 경우이다. 이 경우에서 문제가 되는 이유는 자식노드로 아무 생각없이 대체 할 경우 당연히 이진 검색 트리의 규칙이 무너질 가능성이 있기 때문이다. 우리는 항상 이진 검색트리의 규칙을 무너트리지 않는 경우를 생각해야한다. 즉, 노드의 오른쪽에는 노드 보다 큰것이 노드의 왼쪽에는 노드 보다 작은것이 위치해야 하는것이다.
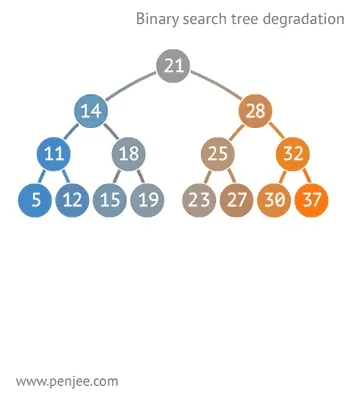
위의 그림에서 보듯이 가장 작거나 가장 큰 원소들은 극단에 있다. 그리고, 규칙을 생각해보면 해당 노드의 바로 이웃 숫자들 왼쪽 서브트리의 최댓값이고 오른쪽 서브트리의 최솟값이다. 왼쪽 서브트리의 최댓값은 왼쪽 서브트리의 오른쪽 하단에 존재하고 오른쪽 서브트리의 최솟값은 왼쪽 하단에 존재한다 혹은 특수한 경우(왼쪽 서브트리에 오른쪽 자식이 없는 경우, 오른쪽 서브트리에 왼쪽 자식이 없는 경우)에는 해당 노드의 자식이 바로 옆 숫자인 경우가 있다. 이 값들을 찾아서 바꾼후에 해당노드를 삭제하면 된다.
02 레드 블랙 트리
혹시, 자바를 사용해본적 있는 독자라면 TreeMap이라는 자료구조를 사용해본적이 있을것이다. 그 TreeMap에서 사용되는것이 레드 블랙 트리이다. 알고있다고 하더라도 레드 블랙 트리에 관해서 공부하다보면 미친듯한 케이스별 동작 방법에 질려버릴 것이다. 이번 포스팅에서 그러한 케이스 없이 레드 블랙 트리를 이해해 볼것이다.
레드 블랙 트리의 핵심은 언제나 항상 검색에 필요한 시간이 O(logn)이 되는 것이다. 이러한 것을 균형잡힌 트리라고 하고 우리의 목표는 색깔을 칠하고 노드들을 돌려서 트리의 높이가 항상 O(logn)이 되게 하는것이다.
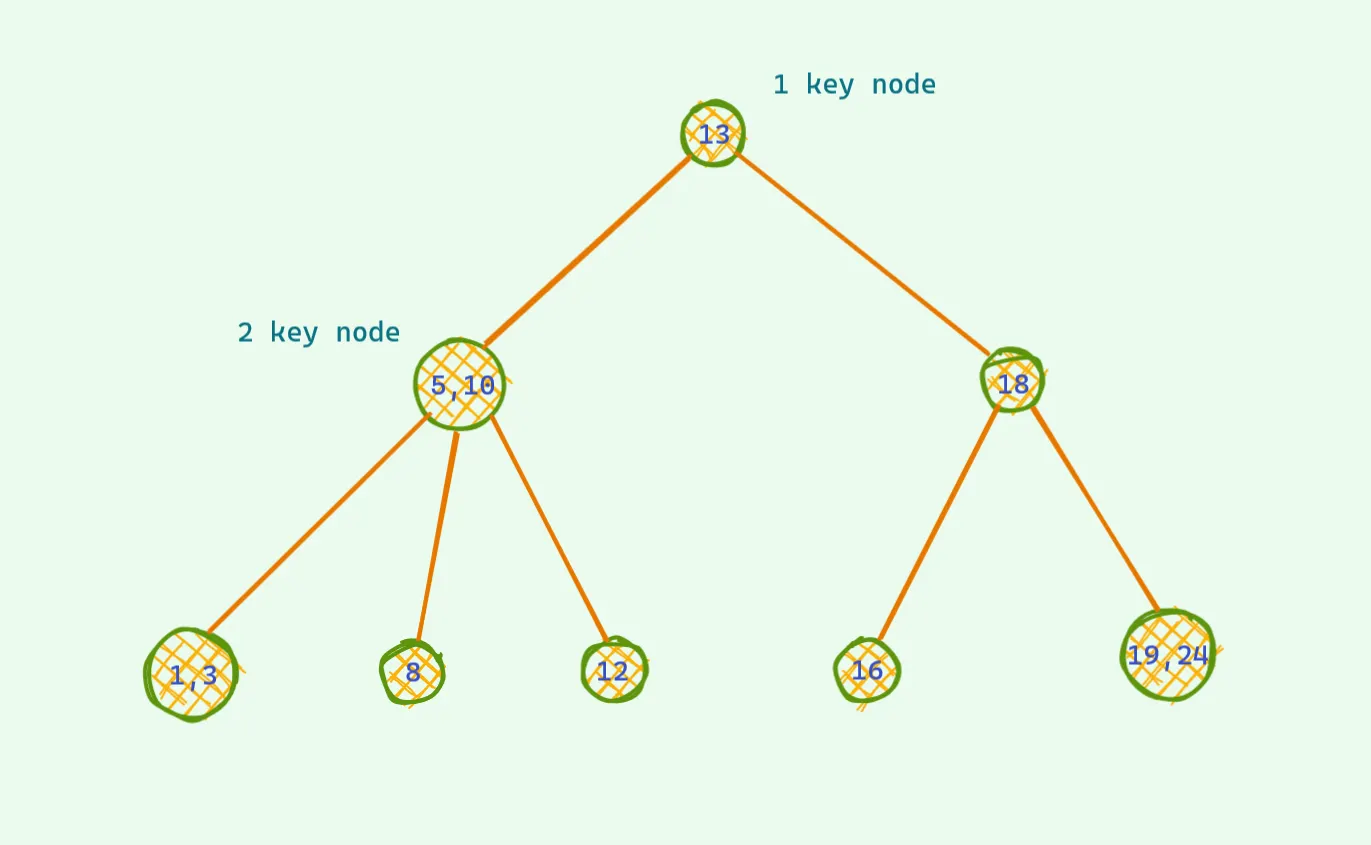
01) 변형된 이진 트리
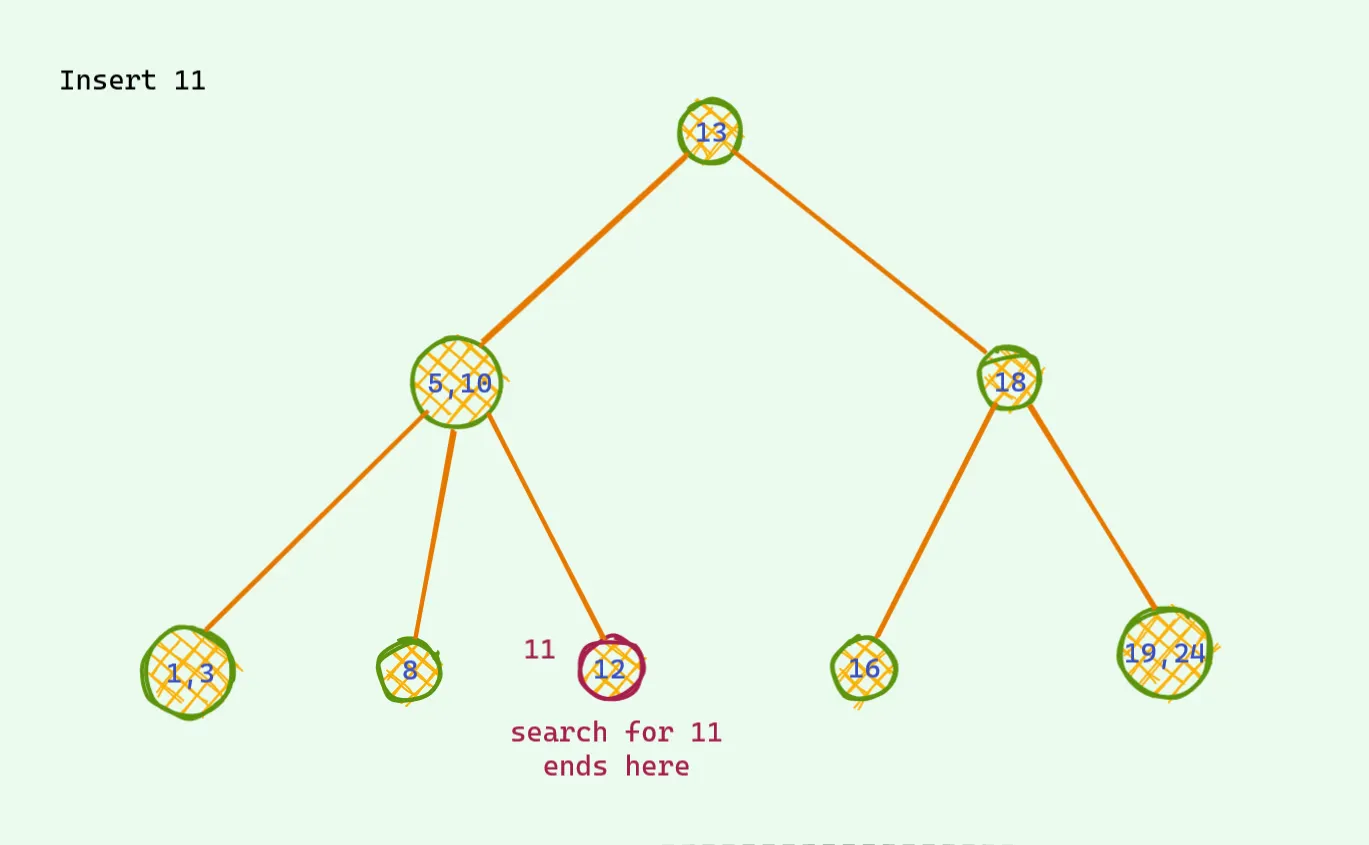
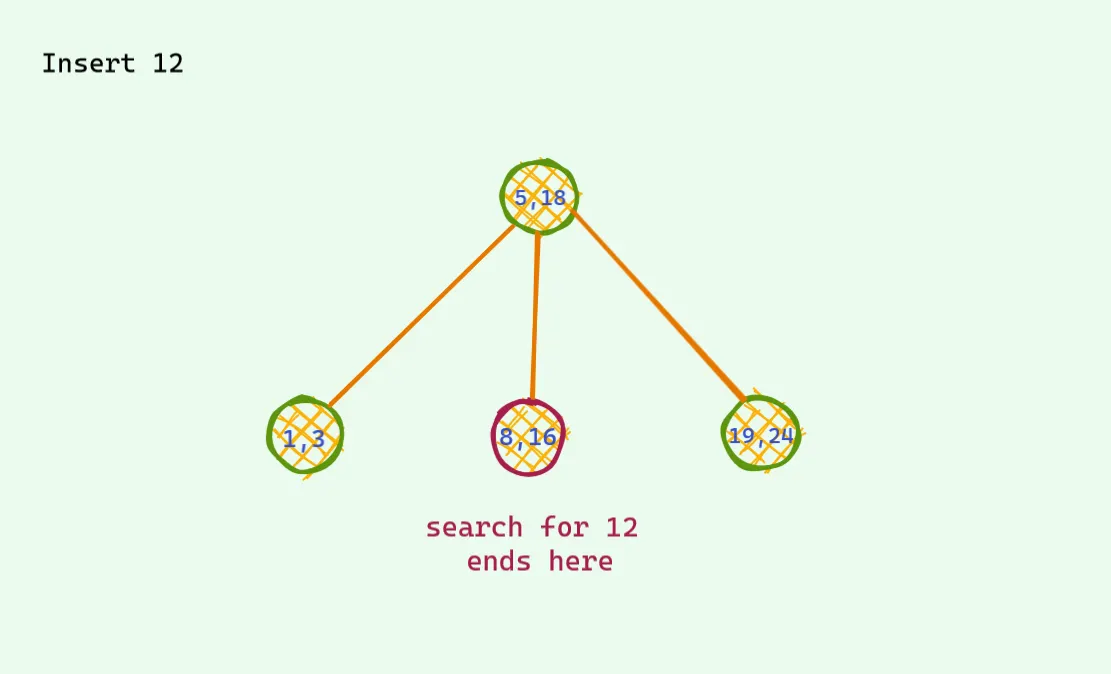
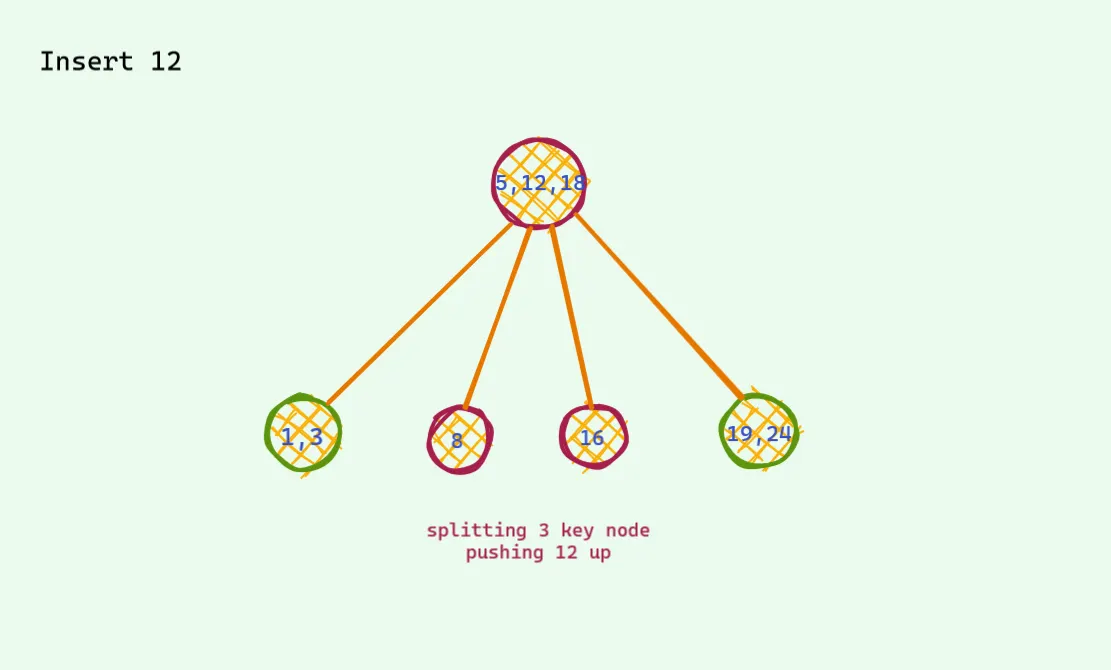
사실 레드 블랙 트리는 살짝 변형된 이진 트리에서 부터 시작된다. 이 트리에서는 키값(노드값)이 최대 두개가 들어갈 수 있고 자식은 최대 세개가 들어갈 수 있다. 왼쪽 값보다 작은 것들은 왼쪽 자식으로 중앙에 있는 값들은 중간 값으로 들어가고 오른쪽 노드보다 큰 값은 오른쪽 노드로 들어가게 된다. 삽입은 어떻게 처리할까? 만약에 트리를 따라가서 도착한 노드가 노드값이 하나밖에 없다면 그냥 해당 값을 규칙에 맞게 넣으면 된다.
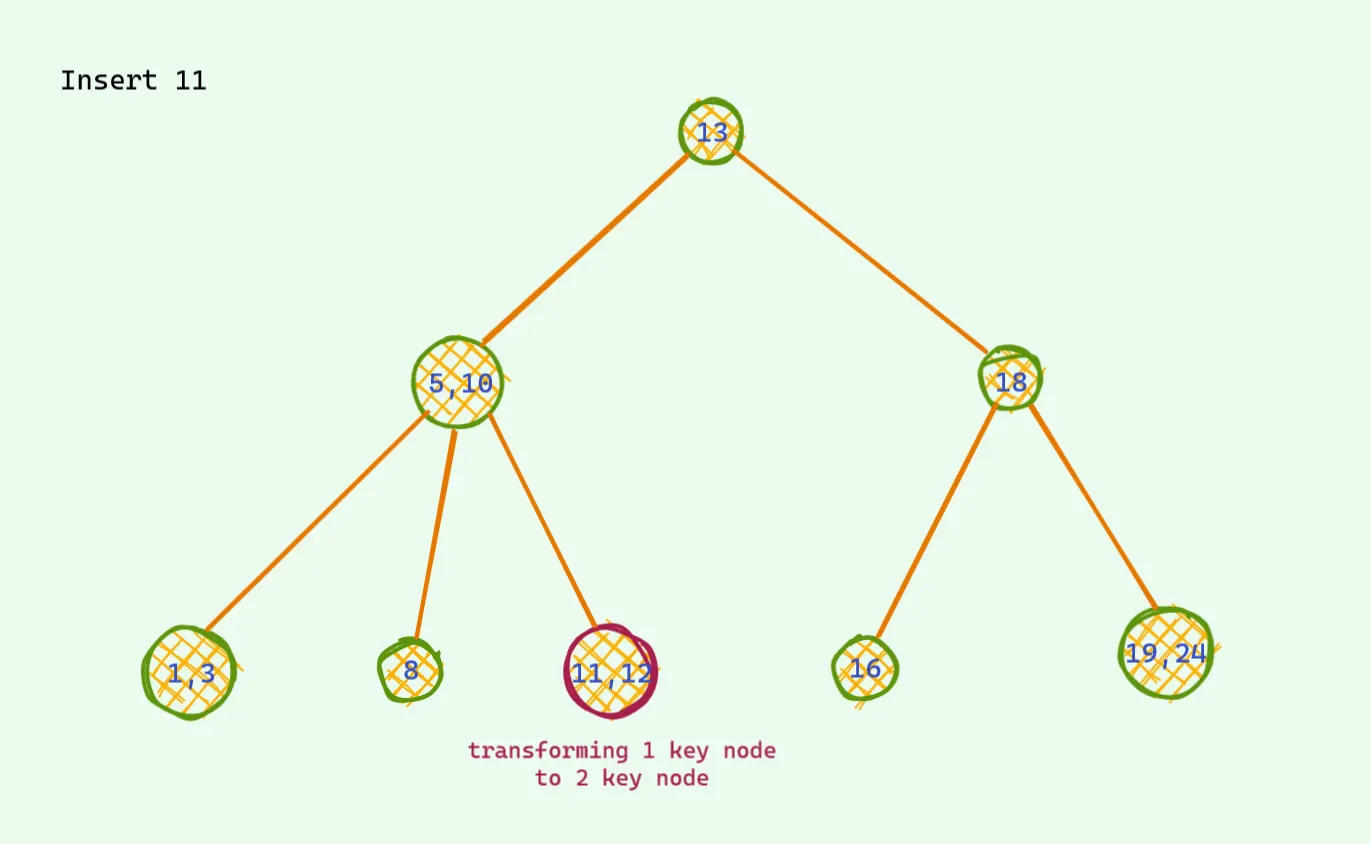
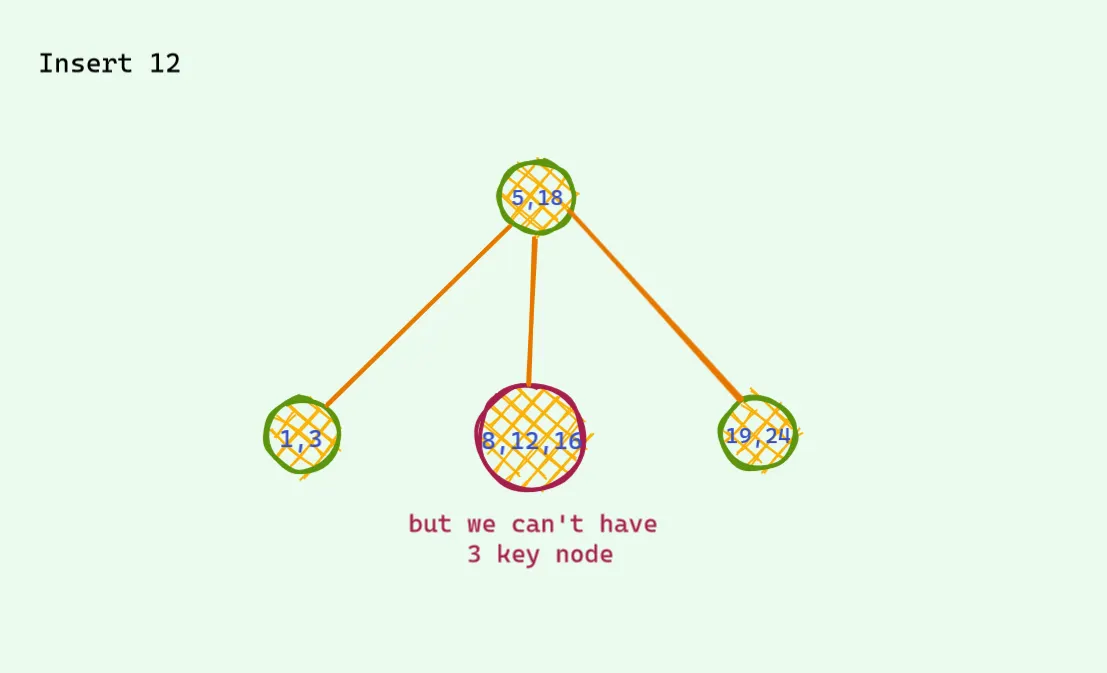
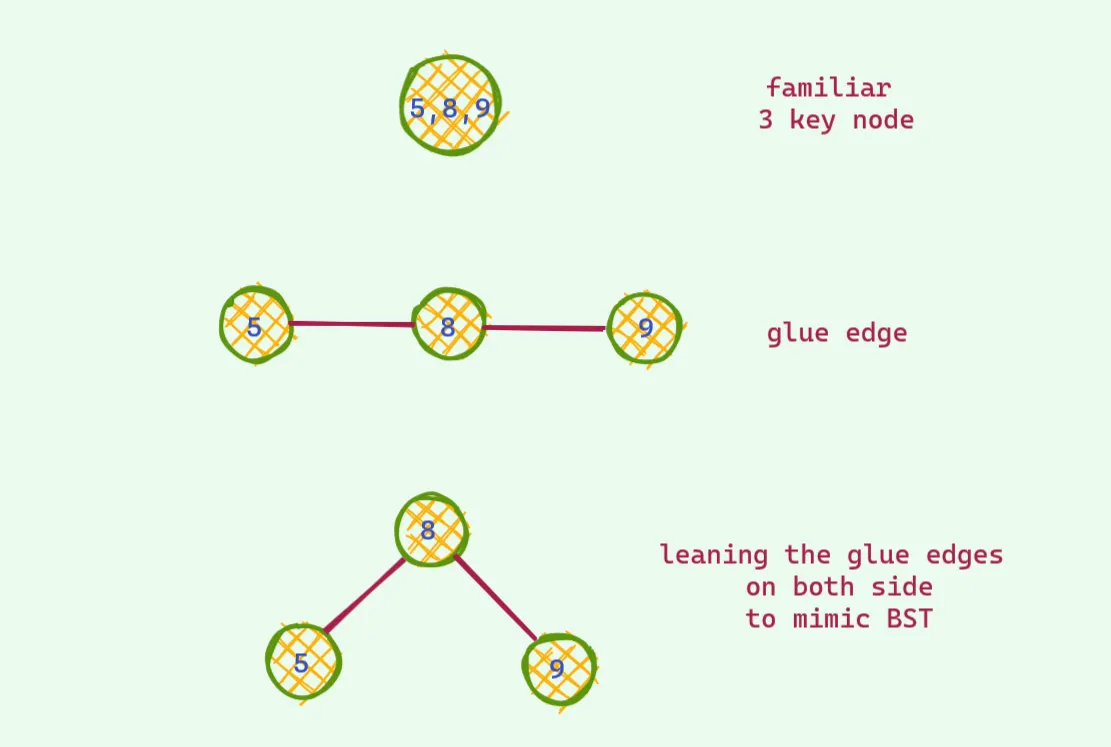
문제는 찾은 노드가 2개의 값을 가지고 있을때 발생한다.
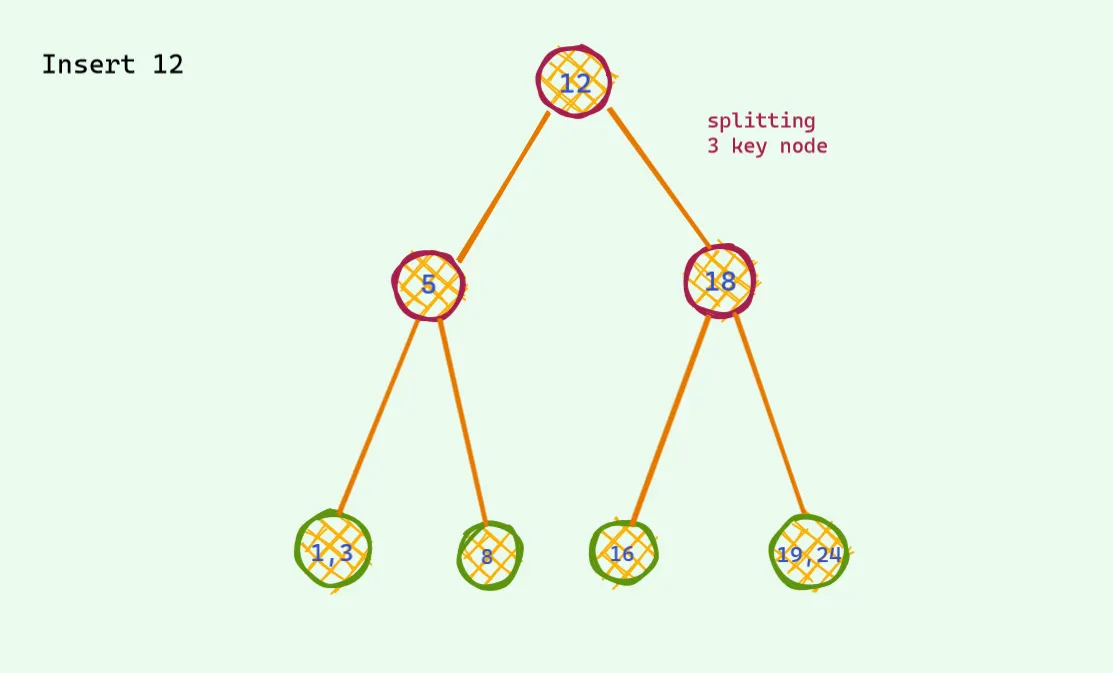
이럴 경우는 3가지 값중에 중앙값을 위로 보내고 자식노드를 세개로 만들면 안정적인 트리가 만들어진다.
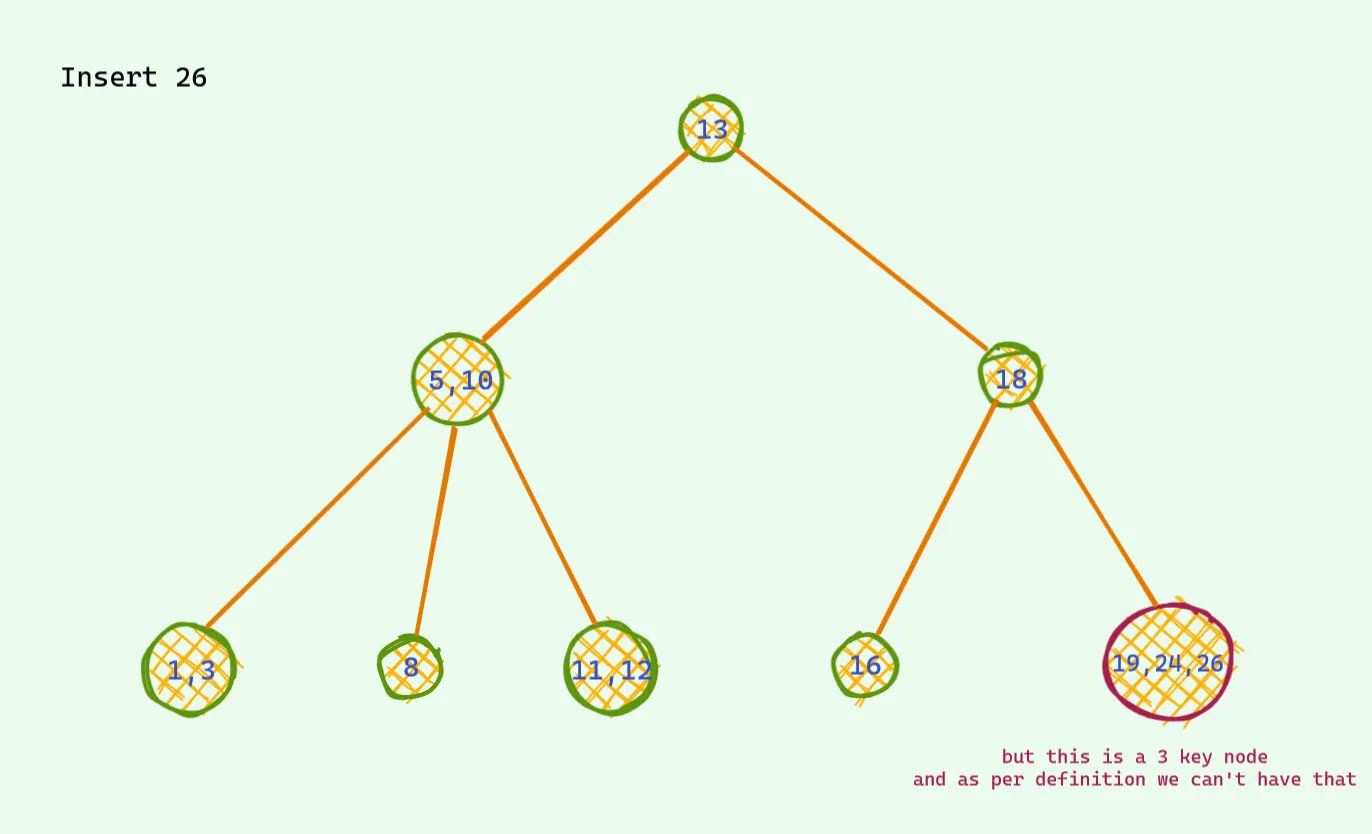
모든 경우에 3개가 되면 이런식으로 처리한다. 예를 들어,
문제가 발생했다.
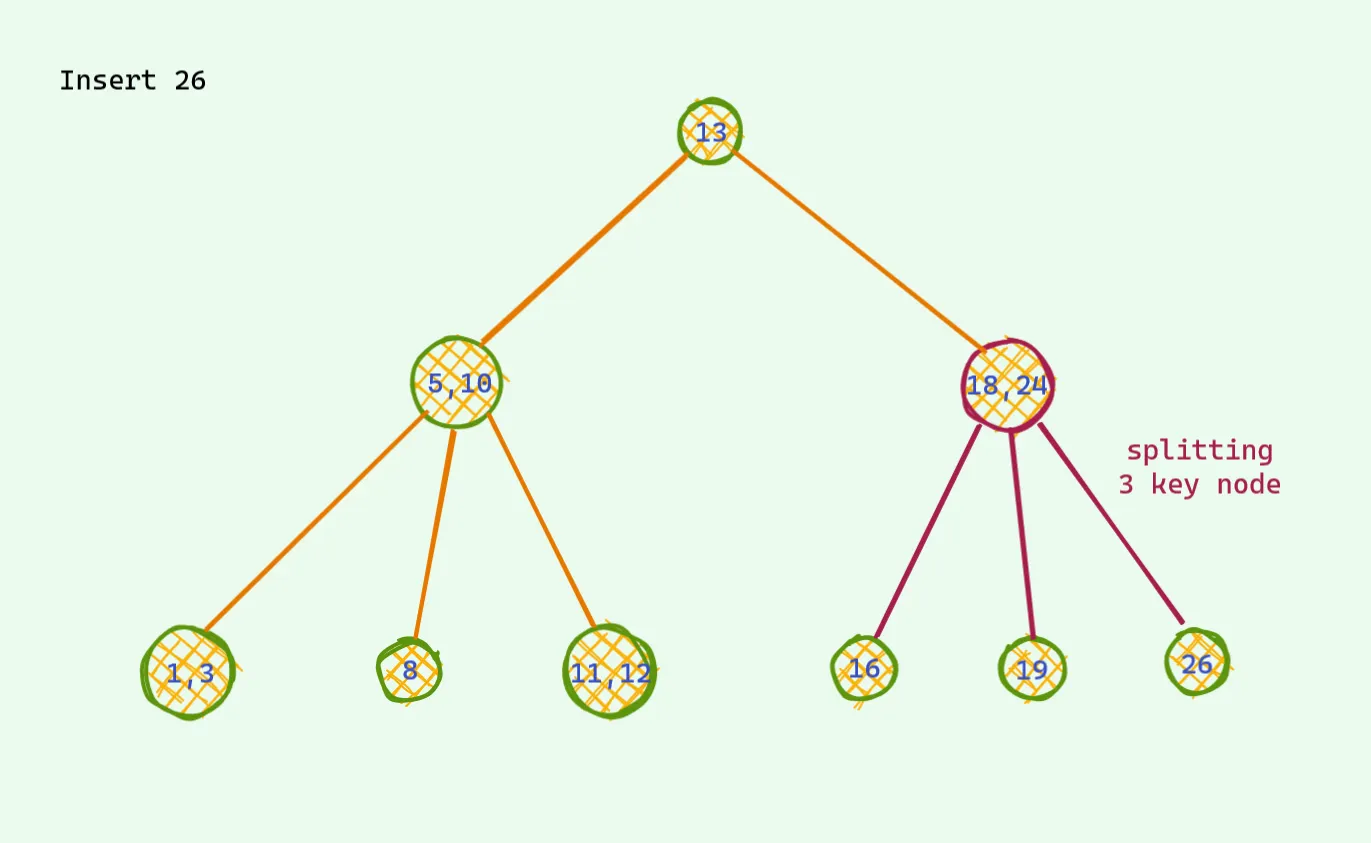
첫번째 문제를 해결 했더니 다시 문제가 부모 노드에서 생겼다.
다시 해결한다.
자 이렇게 문제를 해결하면 삽입의 경우 모든 경우에서 정확히 균형잡힌 트리를 유지할 수 있다는것을 알 수 있다. 이것을 최대 노드값의 갯수가 3이라고 하면 이런식이 된다.
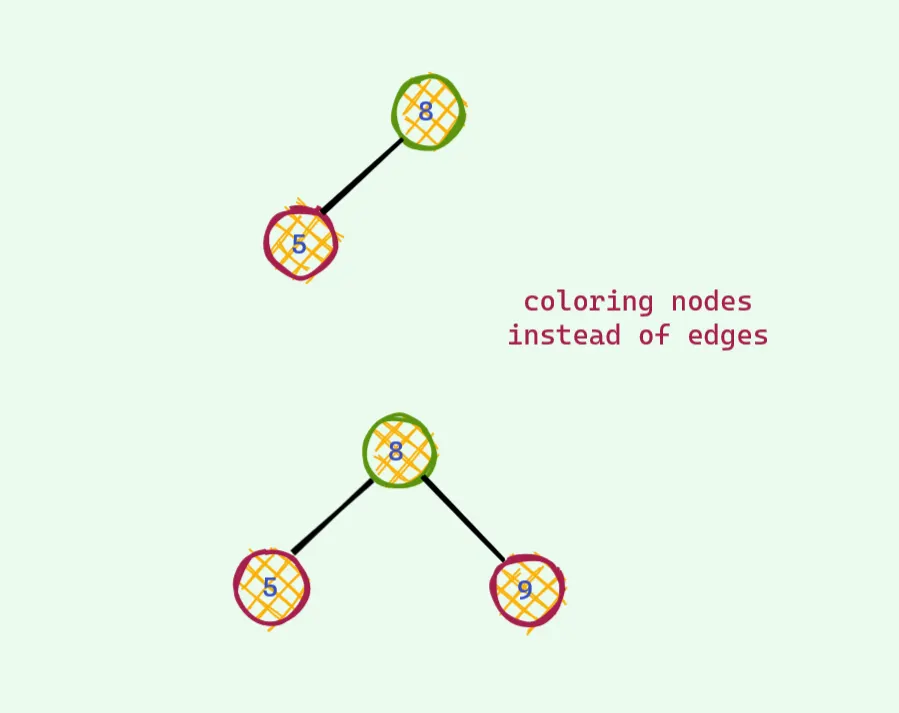
이거랑 레드 블랙트리랑 무슨 상관인가? 자 이제 이 아이디어를 색깔칠하기로 바꾸면 그것이 레드 블랙 트리이다.
짜잔! 이렇게 생각하면 이것이 레드블랙트리다. 깊이 알아보자.
02) 삽입
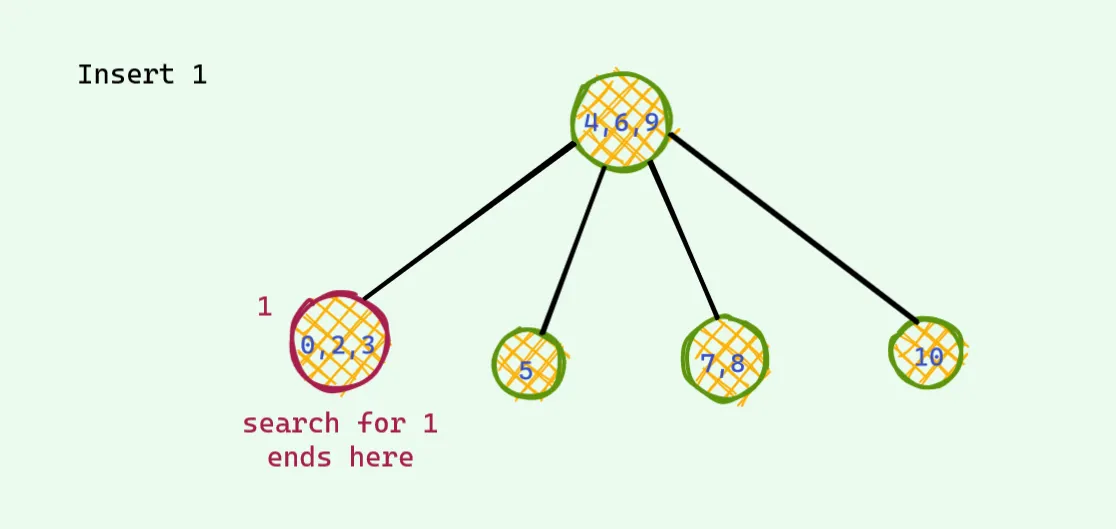
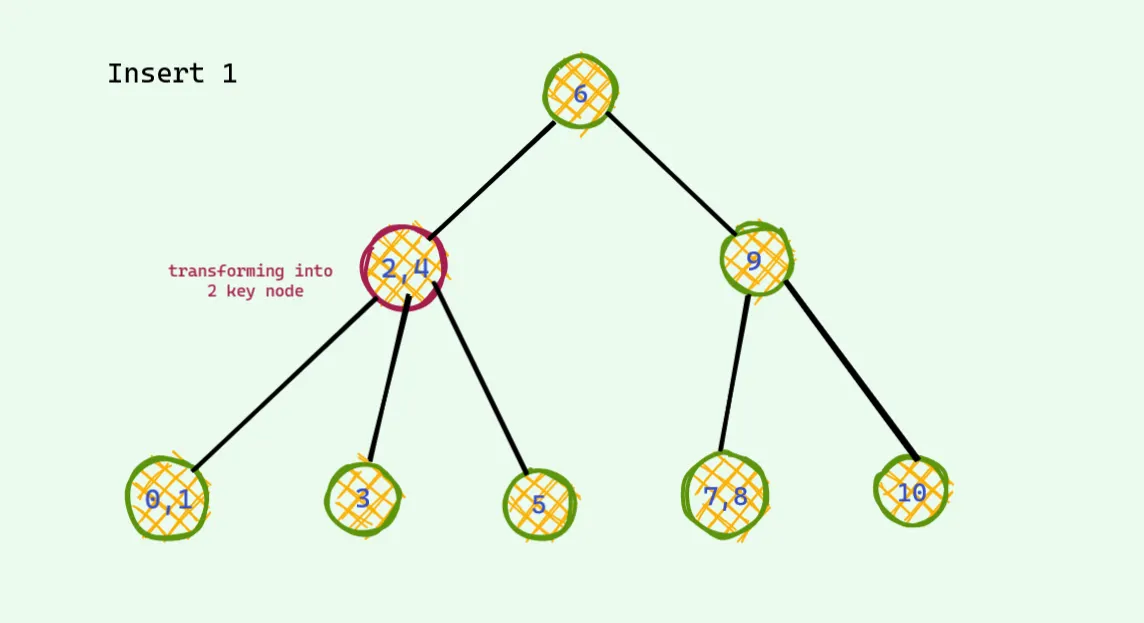
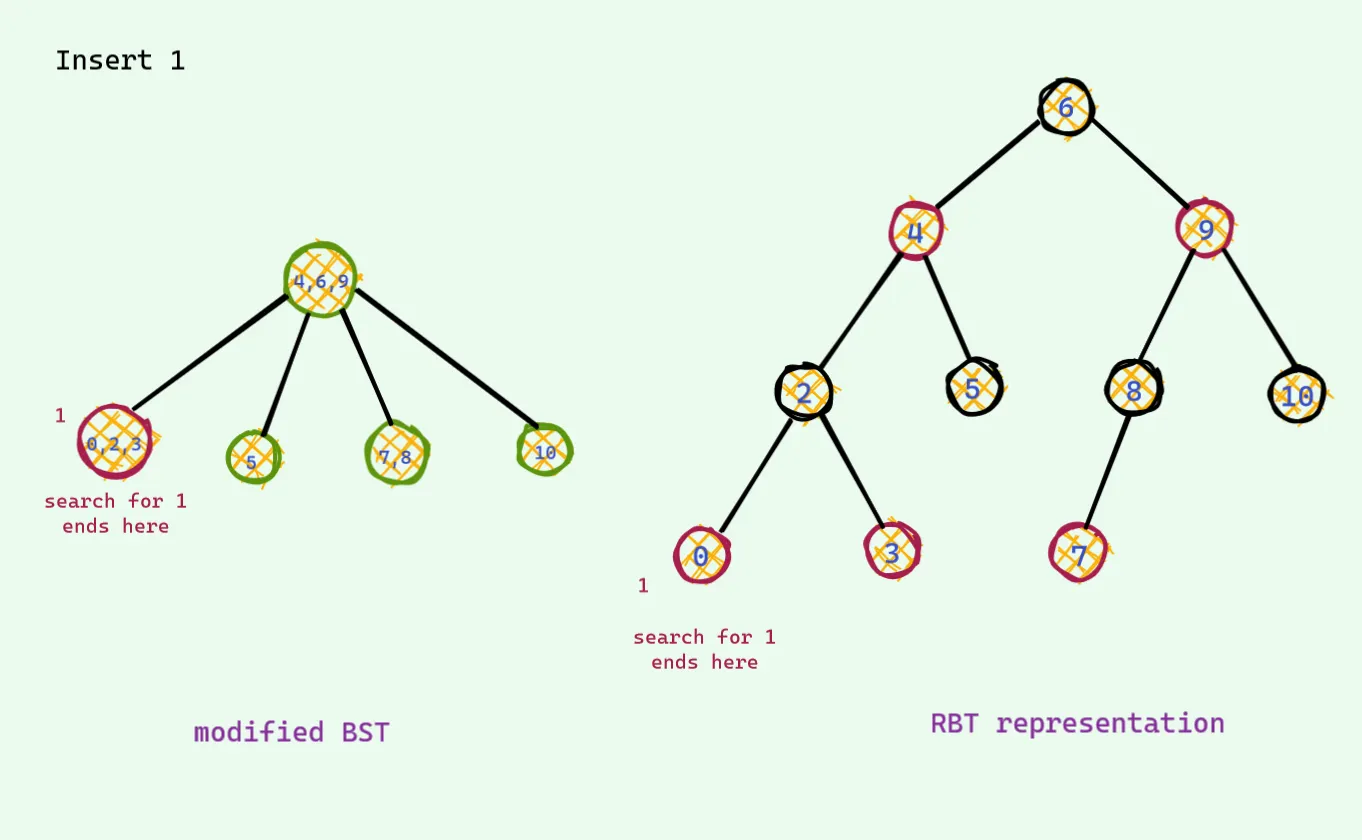
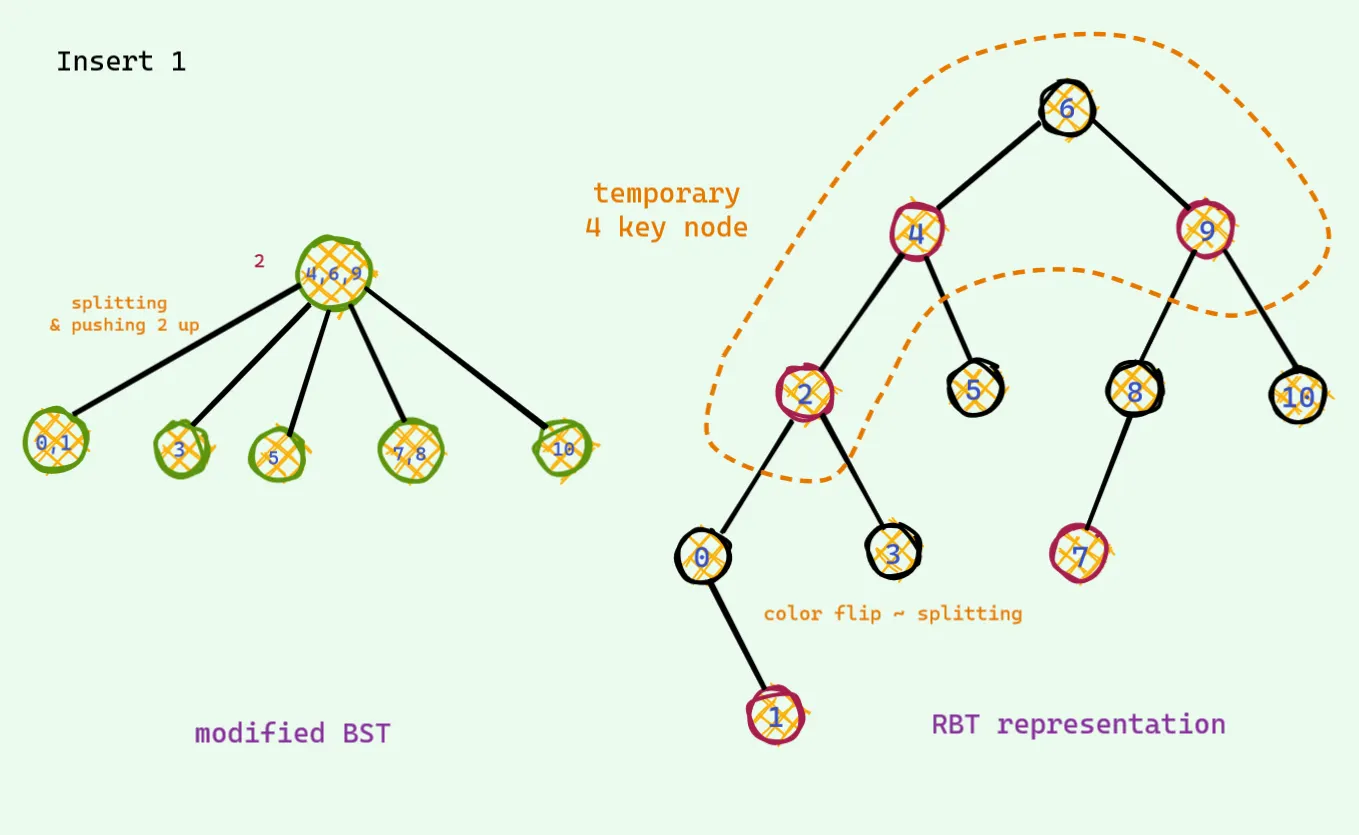
대응되는 트리를 옆에 그려놓고 비교해보자. 1을 넣어 볼것이다.
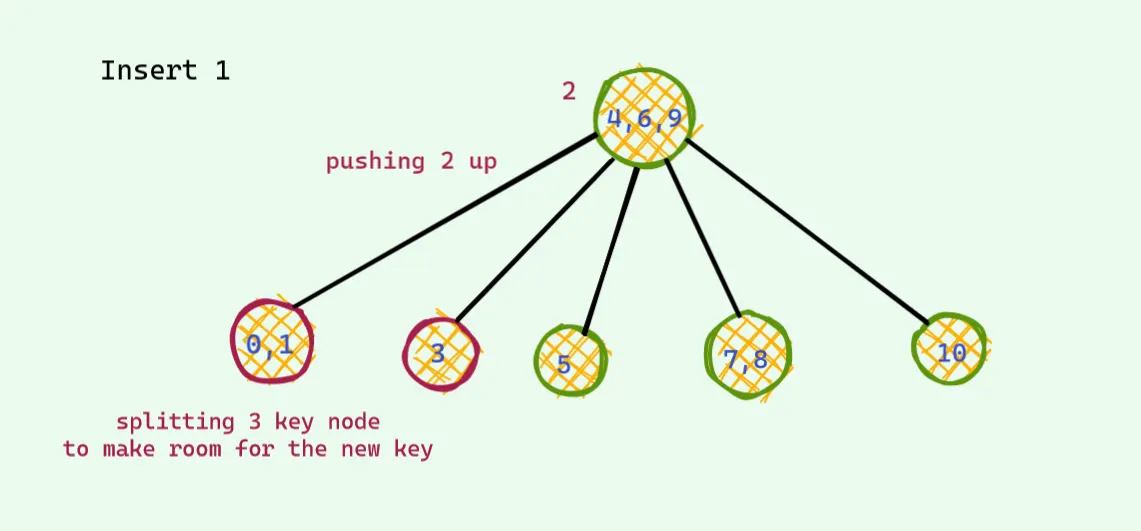
맨왼쪽 노드가 1이 들어가야하기 때문에 중앙 노드가 위로 보내지고 나누어진다. 그러나 다시 루트 노드가 4개가 되는 상황이 발생한다. 레드 블랙 트리에서는 삽입할때는 무조건 빨간색으로 들어가야 하며, 부모도 빨간색 자식도 빨간색인 경우는 나와서는 안된다. 그런 경우가 발생하면 아래의 경우 처럼 컬러 플립이 발생한다(이건 왼쪽의 변형 이진검색트리의 노드값이 4개인 경우와 같은 경우다). 그렇게하면 다시 빨간색 빨간색이 나온다(이건 왼쪽의 변형 이진검색트리의 노드값이 4개인 경우와 같은 경우다).
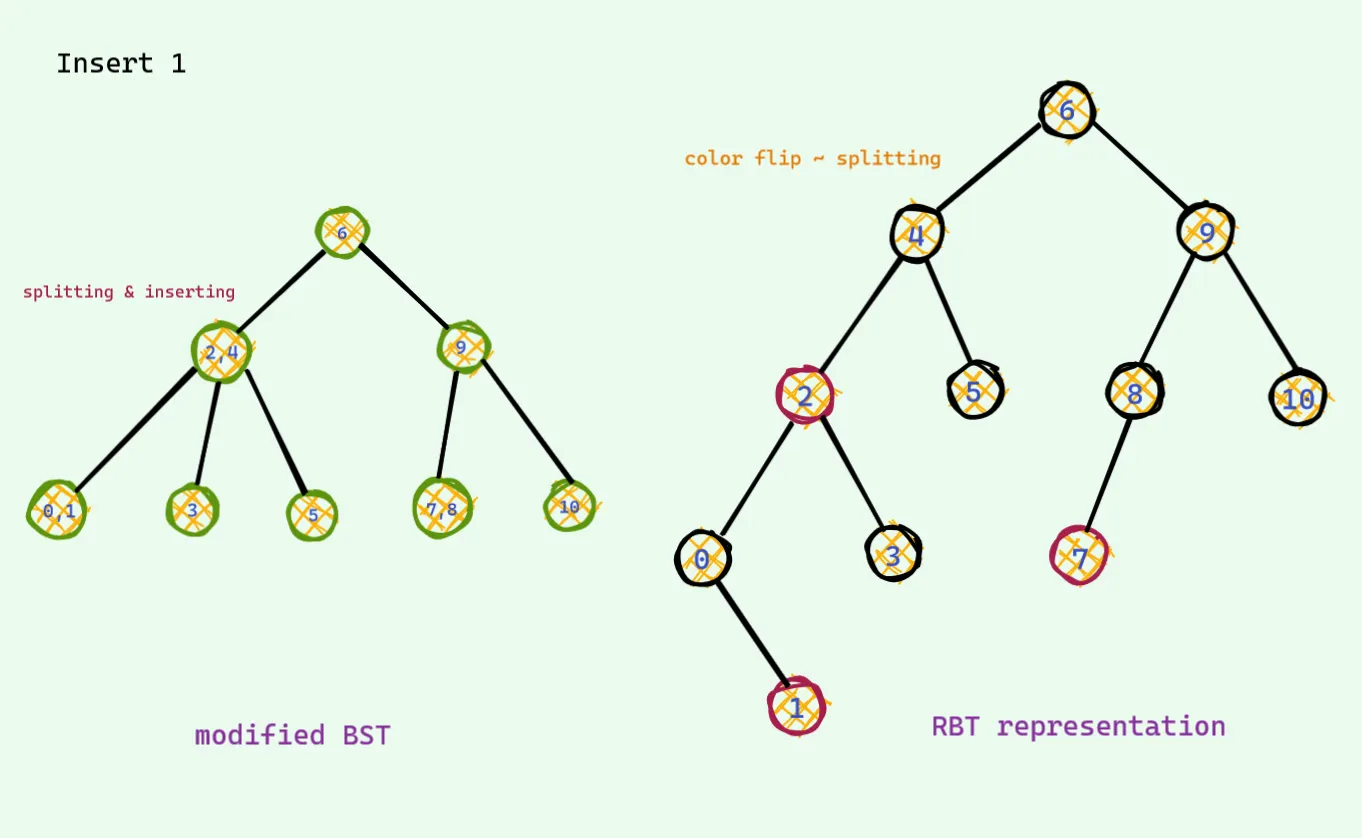
다시 컬러플립을 통해서 문제를 해결한다.
이것이 레드 블랙 트리 삽입의 전부이다. 왼쪽의 경우를 이해했다면, 개념서에 나와있는 빨간색과 빨간색이 연달아 있으면 안된다는 규칙의 이유를 이해한것이다.
04) 삭제
개념서에서 삭제 부분은 미친듯한 케이스들로 정신을 나가게한다. 과연 이것들을 암기하고 있는 것이 과연 의미가 있을까? 싶을 정도이다. 우리는 두개의 큰 개념을 가지고 그 복잡한 문제들을 간단히 해볼 것이다.
•
레드블랙 트리에서 높이란 어떤 리프까지 가던 동일한 갯수의 검은색 노드를 지나친다는 것이다.
•
루트는 항상 검은색이다.
나중에 할련다.