이진탐색트리
이진탐색트리는 자기를 기준으로 작은 값은 왼쪽 자식 노드로 큰 값은 오른쪽 자식 노드로 보내는 트리를 말합니다.
이진탐색트리의 단점
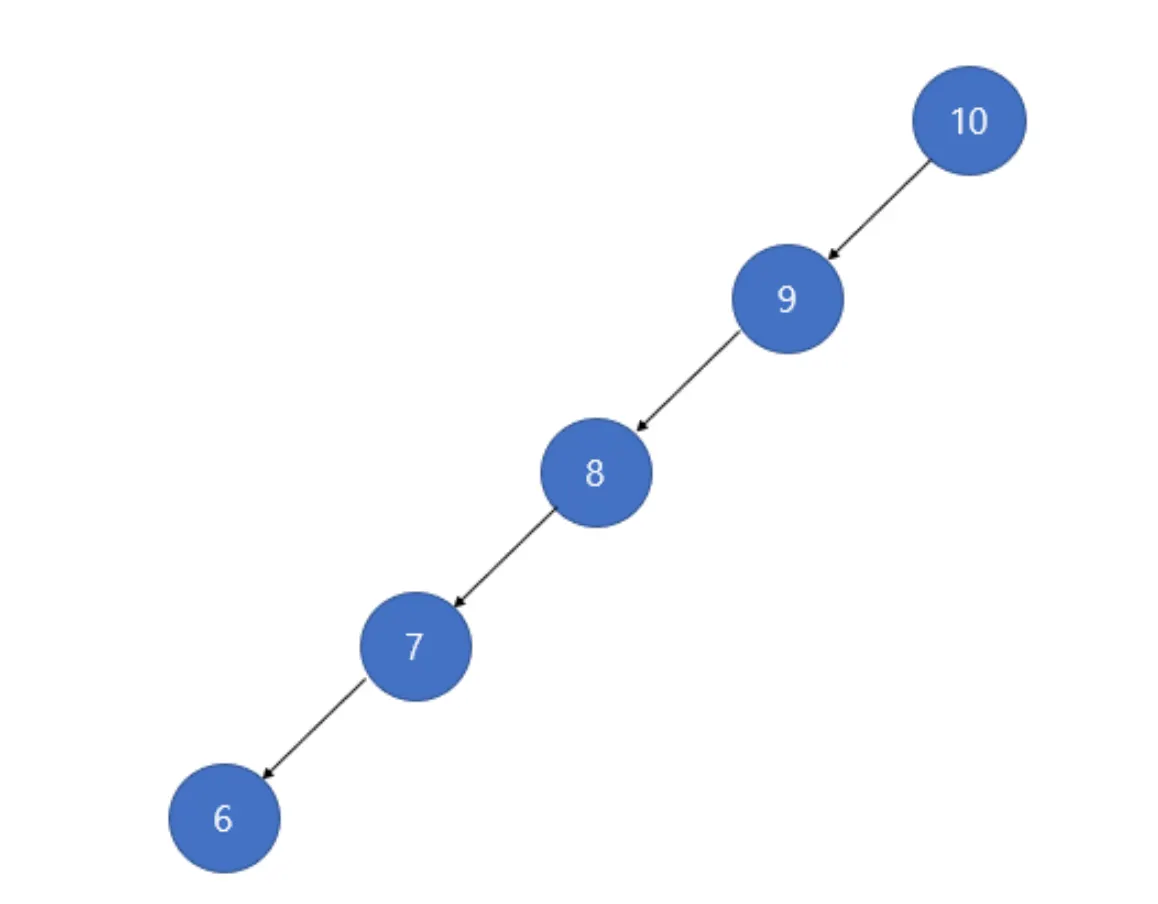
이진탐색트리의 탐색 시간은 O(logN)이지만, 최악의 경우에는 (노드가 한쪽으로 편향되어 있을 경우) O(N)입니다. 이러한 탐색 트리의 단점을 보안하기 위해서는 편향성을 보정해야 합니다. 이를 방법론적으로 만든 것이 바로 자가균형이진탐색트리입니다.
AVL tree
AVL tree는 위에서 말한 것처럼 이진탐색트리의 편향성을 해결하기 위해 고안된 방법입니다. 노드가 새로 들어올 때마다 재귀적으로 리프부터 루트까지 하나씩 balance factor를 검사합니다. 만약 이 때 BF의 절댓값이 1을 넘는다면 해당 노드를 기준으로 그 서브트리를 회전시킵니다. 이런 방식으로 리프부터 루트까지 검사하며 필요한 경우 로테이트를 해 균형을 맞춰주는 것이 AVL tree입니다.
Node
각 노드는 다음과 같은 구조체로 만들어져있습니다. height는 노드의 평향성을 확인하기 위한 수치입니다. 각 노드에서 왼쪽 서브트리의 높이와 오른쪽 서브트리의 높이를 뺀 값을 확인해 그 값이 -1 보다 작거나 +1 보다 크다면 균형을 맞추기 위해 트리를 조정해야 합니다. 이 때 각 서브트리의 높이를 확인하기 위한 수치인 height를 각 서브트리의 루트에 놓는 것입니다.
typedef sturct s_node
{
int data;
int heght; // 내 부모 노드가 내가 속한 서브트리의 깊이를 측정했을 때의 최대 값.
struct t_node *left;
struct t_node *right;
} t_node;
C
복사
height
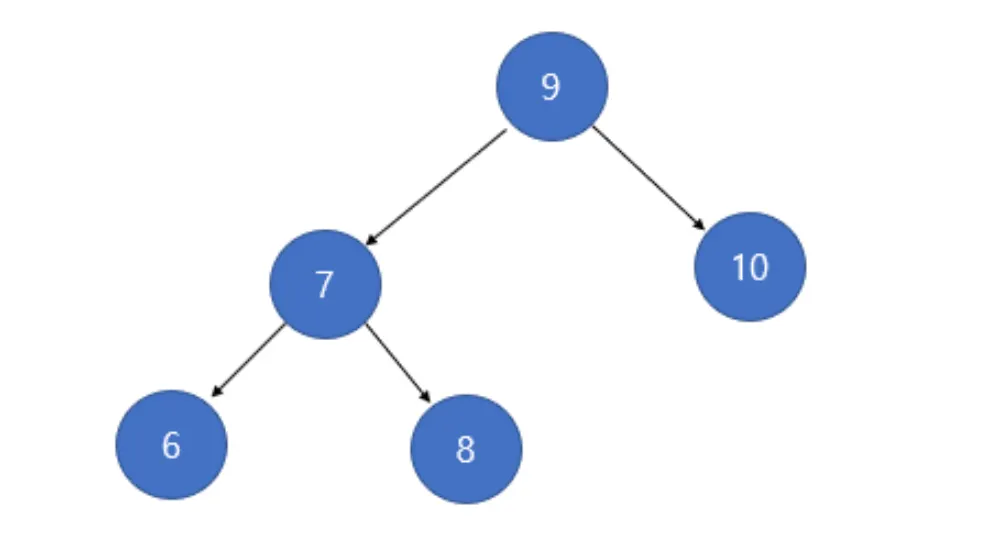
height는 위에서 말했듯이, BF(balance factor)를 확인하기 위한 자료입니다. 노드 9를 기준으로 왼쪽 서브트리의 높이는 2, 오른쪽 서브트리의 길이는 1입니다. 그리고 각 수치를 각 서브트리의 루트에 저장합니다. 그렇기 때문에 노드 7에는 2, 노드 10에는 1이 저장되어야 합니다. 이를 통해 알 수 있는 것은 각 노드는 최초 생성시 무조건 height 값이 1로 초기화되며, 자신의 오른쪽 서브트리외 왼쪽 서브트리 중 가장 height가 큰 것이 자신의 height값이 됩니다.
t_node* create_node(int value)
{
t_node* new_node = (t_node*)malloc(sizeof(t_node));
new_node->value = value;
new_node->left = NULL;
new_node->right = NULL;
new_node->height = 1;
return new_node;
}
void update_height(t_node* node)
{
node->height = 1 + max(height(node->left), height(node->right));
}
C
복사
rotate operation
나(노드)를 기준으르 현재 서브트리릐 높이 차이가 1을 초과한다면 트리의 높이를 재조정해야 합니다. 재조정 단계에서 행하는 기본 오퍼레이션은 2가지 입니다. 오른쪽으로 돌리거나, 아니면 왼쪽으로 돌리거나. 각 방법에 대해 배워봅시다.
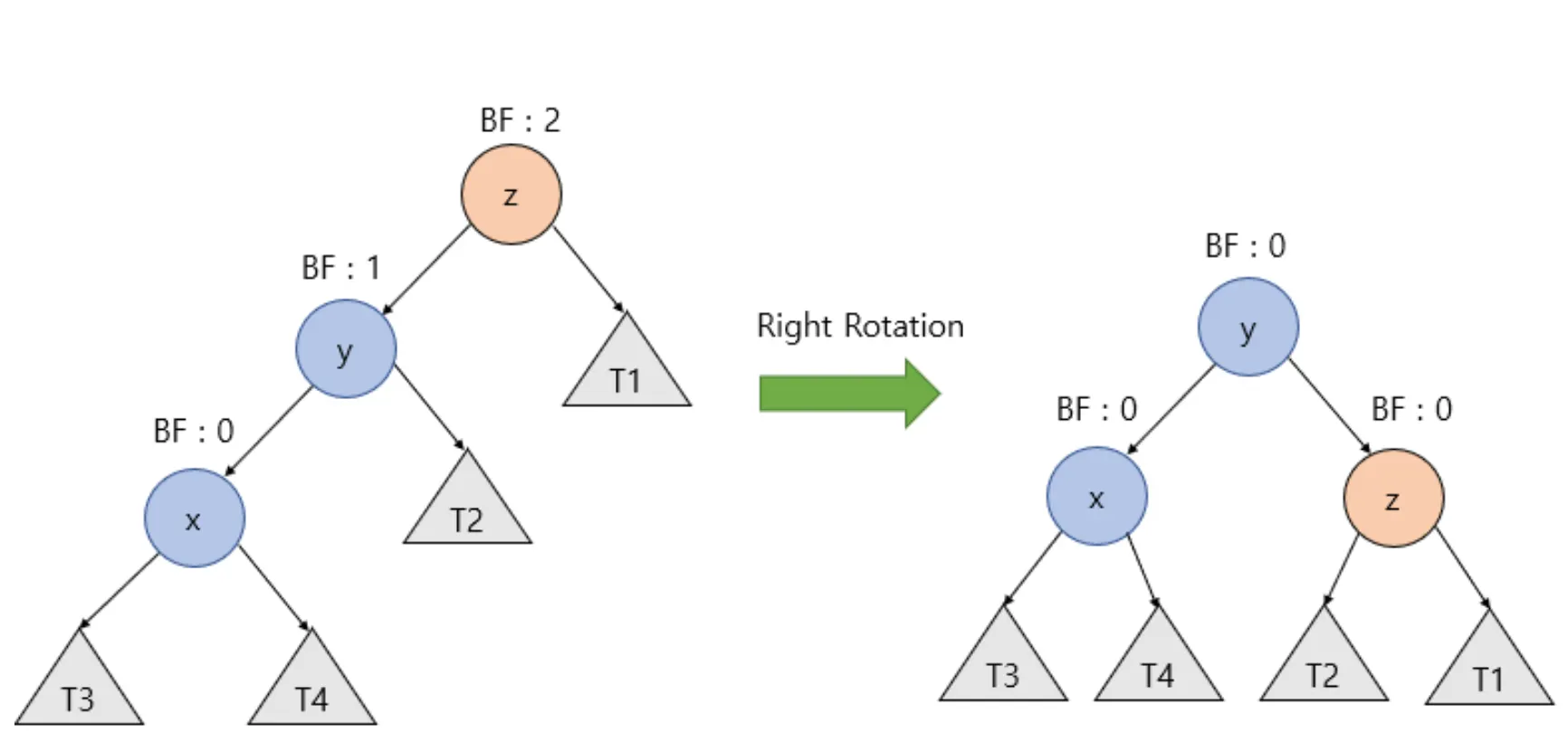
rotate right
나를 기준으로 노드가 좌-좌로 편향되어 있을 때 오른쪽으로 돌립니다. 나(z), 좌(y), 좌-좌(x)라고 하면, 나(z)가 좌(y)의 오른쪽 자식으로 들어갑니다. 좌(y)가 오른쪽 자식이 있을 수 있으므로 이를 T2라고 하고 T2를 나(z)의 왼쪽 자식으로 지정합니다.
t_node* rotate_right(t_node* z)
{
t_node* y = z->left;
t_node* t2 = y->right;
y->right = z;
z->left = t2;
update_height(z);
update_height(y);
return y;
}
C
복사
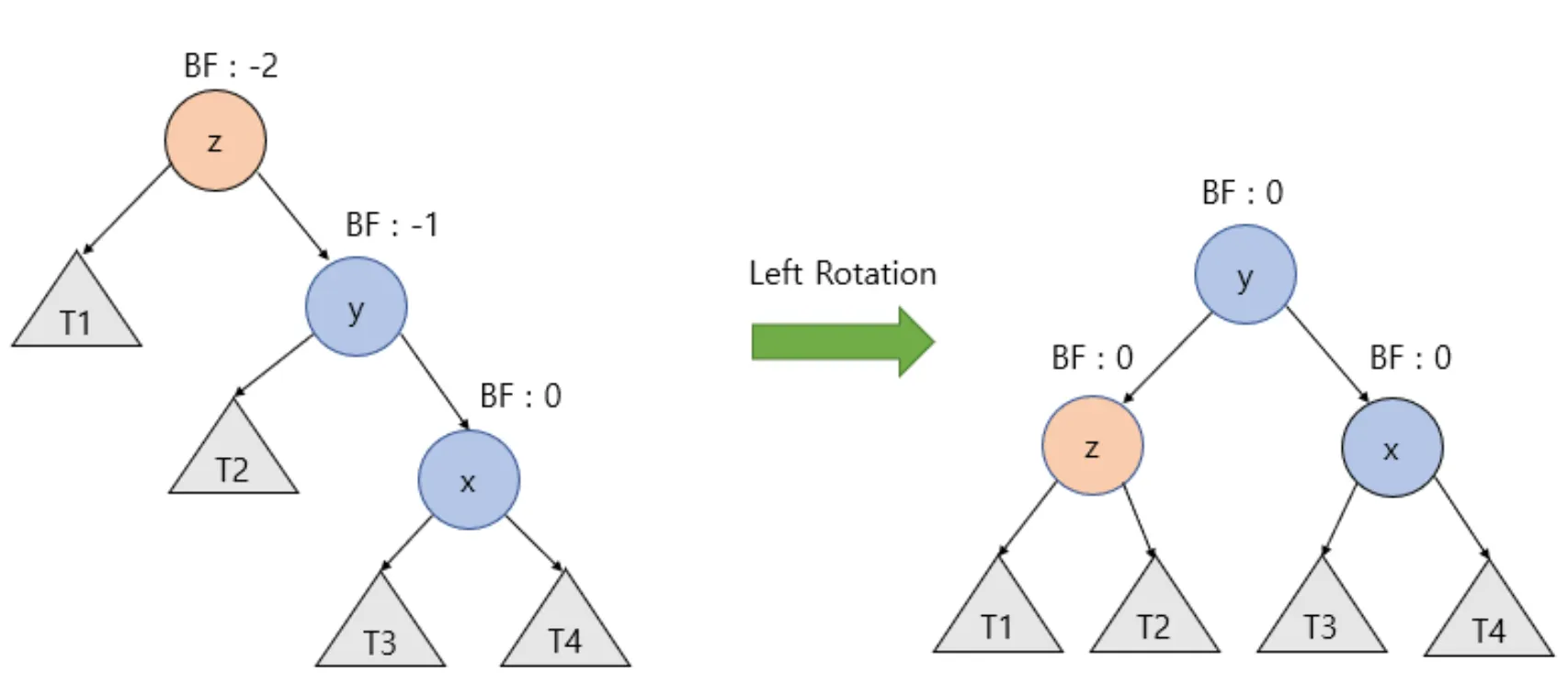
rotate left
나를 기준으로 노드가 우-우로 편향되어 있을 때 오른쪽으로 돌립니다. 나(z), 우(y), 우-우(x)라고 하면, 나(z)가 좌(y)의 왼쪽 자식으로 들어갑니다. 오ㅜ(y)가 왼쪽 자식이 있을 수 있으므로 이를 T2라고 하고 T2를 나(z)의 오른쪽 자식으로 지정합니다.
t_node* rotate_left(t_node* z)
{
t_node* y = z->right;
t_node* t2 = y->left;
y->left = z;
z->right = t2;
update_height(z);
update_height(y);
return y;
}
C
복사
insert
이제 기본 AVL tree의 기본 동작을 알았으니, 루트부터 노드를 push합시다. 노드를 삽입하면 루트노드 부터 시작해 내려가며 값을 비교합니다. 각 노드와 값을 비교해 노드보다 작다면 그 노드의 왼쪽 자식으로, 크다면 오른쪽 자식으로 내려갑니다. 단계적으로 내려가면서 자식의 노드가 비어있을 때 까지 내려갑니다. 이 때 insert 함수는 재귀적으로 동작하는데, 노드를 리프에 삽입한 후 스택에 쌓인 함수들이 종료되면서 노드를 타고 루트까지 올라갑니다. 루트까지 올라가면서 각 노드의 BF를 검사하고 BF에 문제가 있다면 rotate를 진행합니다.
t_node* insert(t_node* node, int value)
{
int balance;
if (node == NULL)
return (create_node(value));
if (value < node->value)
node->left = insert(node->left, value);
else if (value > node->value)
node->right = insert(node->right, value);
else
return node;
update_height(node);
balance = height(node->left) - height(node->right);
if (balance > 1)
{
if (value < node->left->value)
return rotate_right(node);
else
{
node->left = rotate_left(node->left);
return rotate_right(node);
}
}
else if (balance < -1)
{
if (value > node->right->value)
return rotate_left(node);
else
{
node->right = rotate_right(node->right);
return rotate_left(node);
}
}
return node;
}
C
복사
The code
다음은 전체 코드입니다.
#include <stdio.h>
#include <stdlib.h>
#define TRUE 1
#define FALSE 0
typedef struct node
{
int value;
int height;
struct node* left;
struct node* right;
} t_node;
int height(t_node* node)
{
if (node == NULL)
return 0;
return node->height;
}
int max(int a, int b)
{
if (a > b)
return a;
return b;
}
t_node* create_node(int value)
{
t_node* new_node = (t_node*)malloc(sizeof(t_node));
new_node->value = value;
new_node->left = NULL;
new_node->right = NULL;
new_node->height = 1;
return new_node;
}
void update_height(t_node* node)
{
node->height = 1 + max(height(node->left), height(node->right));
}
t_node* rotate_right(t_node* z)
{
t_node* y = z->left;
t_node* t2 = y->right;
y->right = z;
z->left = t2;
update_height(z);
update_height(y);
return y;
}
t_node* rotate_left(t_node* z)
{
t_node* y = z->right;
t_node* t2 = y->left;
y->left = z;
z->right = t2;
update_height(z);
update_height(y);
return y;
}
t_node* insert(t_node* node, int value)
{
int balance;
if (node == NULL)
return (create_node(value));
if (value < node->value)
node->left = insert(node->left, value);
else if (value > node->value)
node->right = insert(node->right, value);
else
return node;
update_height(node);
balance = height(node->left) - height(node->right);
if (balance > 1)
{
if (value < node->left->value)
return rotate_right(node);
else
{
node->left = rotate_left(node->left);
return rotate_right(node);
}
}
else if (balance < -1)
{
if (value > node->right->value)
return rotate_left(node);
else
{
node->right = rotate_right(node->right);
return rotate_left(node);
}
}
return node;
}
int main()
{
t_node* root = NULL;
root = insert(root, 10);
root = insert(root, 20);
root = insert(root, 30);
root = insert(root, 40);
root = insert(root, 35);
printf("root:%d\n", root->value);
printf("root->left:%d\n", root->left->value);
printf("root->right: %d\n", root->right->value);
printf("root->right->left: %d\n", root->right->left->value);
printf("root->right->right: %d\n", root->right->right->value);
return 0;
}
JavaScript
복사