Dynamic Programming

GeeksforGeeks에 의하면 DP는 Sub-Problem들로 나누어 결과 값을 저장함으로써 계산 수를 줄이는 것을 말한다.

그러나 위는 그저 정의이고 실제로 풀 때는 다음과 같은 접근 방법이 편할 것이다. DP는 문제들을 작은 Sub-Problem으로 쪼개어 Sub-Problem 간의 상관 관계에 집중하여 결과적으로 전체 Problem을 푸는 방법이다.

조금 더 친근하게 말하기 위해 계단에 비유해 보겠다. 우리가 $n$번째 계단을 밟기 위해서는 $n-1, n-2, n-3, ..., 1$번째 계단들을 밟아야 한다. 순서대로 계단을 밟는다면 끝에 도달할 수 있다. 문제가 주어졌을 때 계단으로 바꾸어 생각해 보도록 한다. 어떠한 상태에서 다음 상태로 나아가기 위해 무슨 일을 해야하는지 고민하고 처음 상태와 끝 상태를 고려하면 문제는 풀린다.

피보나치 수열을 예로 들어보자.

$f_{10}$을 계산하기 위해서 재귀 함수를 이용한다면 $f_{10}$을 계산할 때 $f_5$가 필요할 때마다, $f_4, f_3, f_2, f_1, f_0$을 계산해야 한다. 이렇게 푼다면 굉장히 비효율적이지 않은가? 이 방법 대신에, 이전 두 값을 알 때 다음 값을 알 수 있다는 점을 고려하여 $f_2, f_3, f_4 ...$ 순서로 계산해 나간다면 쉽게 풀 수 있다는 것을 유추할 수 있다.

이처럼 임의의 $n$번째 Sub-Problem에 대하여, $n+1$ 번째 Sub-Problem을 구할 수 있다면 DP로 풀 수 있다. 또한 이 때 반드시 처음 Sub-Problem과 마지막 Sub-Problem을 고려해야 한다. 경계 값에서 프로그램이 버그를 일으킬 가능성이 높기 때문이다. 나중에 문제의 난이도가 조금 더 상승한다면, 임의의 $(n,m)$ Sub-Problem에 대하여 $(n+1, m)$과 $(n, m+1)$ 번째 Sub-Problem을 구할 수 있을 때 2차원 DP도 풀 수 있다. DP의 원리를 잘 파악한다면 보다 어려운 3, 4원 DP 문제들도 풀 수 있을 것이다. (ㅋㅋㅋㅋㅋㅋ..)

대부분 눈치를 챘겠지만, 점화식으로 나타낼 수 있는 모든 수열은 DP로 풀 수 있다. 하지만 이 말이 곧 점화식으로 나타낼 수 있다면 무조건 DP로 풀어야 한다는 것은 아니다. 반례로 피보나치 수열을 구하는 O(logn)의 시간 복잡도를 가지는 DP가 아닌 알고리즘이 있다.

코딩 테스트에 자주 나오는 DP 문제들은 경우의 수를 파악하는 문제, 조합을 구하는 문제, LIS (Longest Increasing Subsequence) 정도로 요약할 수 있다.

보통 기초적인 문제들이 많고 Sub-Problem으로 나누는 것만 생각하면 쉽게 풀 수 있다.

조합의 공식은 다음과 같다.

이를 공식대로 팩토리얼을 이용해서 풀면 매우 빠르게 Overflow가 나와서 잘못된 값을 얻게 된다. 조합에 대한 공식은 위의 것 말고 한 가지가 더 있다. 이 공식을 활용하면, 중간 계산 과정에서 더 큰 값이 등장하지 않기 때문에 Overflow를 피할 수 있다.

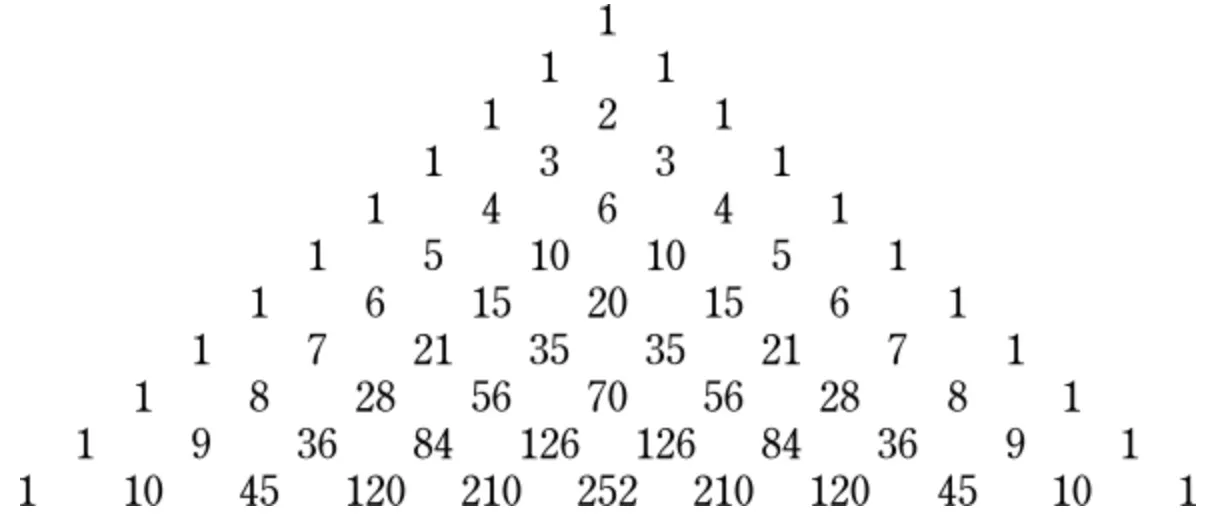
파스칼의 삼각형은 위 공식을 시각적으로 볼 수 있는 삼각형이다. 파스칼의 삼각형은 아래와 같다.

파스칼의 삼각형을 잘 생각해보면, $n$번째 줄을 알면 $n+1$번째 줄을 알 수 있고 중간 계산 과정에서 최종 결과보다 큰 값이 나오지 않는 것을 알 수 있다. 따라서 최종 결과 값이 Overflow가 발생하지 않는 값이라면, 이 방법을 통해서 문제 없이 정답을 구할 수 있는 것을 알 수 있다. 대부분의 조합 문제는 주어진 문제가 조합을 구해야하는 문제인지 파악만 하면 쉽게 풀 수 있다.

LIS는 Longest Increasing Subsequence의 약자로 주어진 수열의 최장 부분 수열을 구하는 문제이다. LIS를 구하는 유명한 방법으로는 이분 탐색으로 O(nlogn)만에 구하는 알고리즘도 있지만, DP를 통해서도 풀 수 있다.

DP를 통해서 LIS를 푸는 방법은 수열의 원소를 하나씩 보면서 해당 원소로 끝나는 LIS의 길이를 추적하면 LIS를 구할 수 있다. 임의의 원소로 끝나는 LIS를 구하기 위해선 자기보다 앞서면서 자기보다 작은 원소로 끝나는 LIS 중 가장 긴 LIS를 찾아야 한다. 그 때 찾은 LIS 뒤에 해당 원소를 더하면 그게 해당 원소로 끝나는 LIS 이기 때문이다.

예를 들어보자.

제일 앞에 있는 $1$의 경우 자신보다 앞선 원소가 없기 때문에 첫 번째 원소로 끝나는 LIS는 $1$이다.

그 다음 원소인 $6$을 보면 자신보다 앞서면서 자신보다 작은 원소는 $1$로 1개가 있다. 따라서 $6$으로 끝나는 LIS는 $1,6$이 된다.

그 다음 원소인 $2$를 보면 자신보다 앞서면서 자신보다 작은 원소는 $1$로 1개가 있다. 따라서 $2$로 끝나는 LIS는 $1, 2$가 된다.

그 다음 원소인 $5$를 보면 자신보다 앞서면서 자신보다 작은 원소는 $1$과 $2$가 있다. 이 때, $1$로 끝나는 LIS는 $1$이고, $2$로 끝나는 LIS는 $1,2$이다. 따라서 보다 긴 $1, 2$를 붙여서 $5$로 끝나는 LIS는 $1,2,5$가 된다.

이처럼 각 원소마다 해당 원소로 끝나는 LIS를 추적한 후에 그 중에서 가장 긴 LIS를 찾으면 문제를 해결할 수 있다.

메모이제이션은 중복 계산을 피하는 계산 최적화 기법을 말한다. DP 문제를 풀다보면 같은 값을 계속 호출하는 경우가 많다. 지금은 피보나치 수열을 계속해서 계산해야 한다고 가정해보자. 처음에 $f_{100}$의 값이 필요하고, 그 직후에 $f_{50}$ 값이 필요하다면 이 두 값을 계산하기 위해서 피보나치 수열 계산을 따로 따로 할 필요가 없다는 것이다. 피보나치 수열을 DP 방식으로 계산했다고 가정할 때, $f_{100}$을 계산하는 과정에서 $f_0$부터 $f_{99}$까지 계산하게 된다. $f_{100}$을 계산하는 동안 그 전 값들을 배열에 저장한다면, $f_{50}$을 다시 계산할 필요 없이 바로 값을 구할 수 있다. 메모이제이션은 특별히 어렵지도 않고 DP 외에도 많이 사용되니 이 개념을 익혀두면 좋다.