벡터 내적
여기서 말하는 벡터는 C++의 std::vector가 아니라 수학에서의 벡터입니다.
게임, 특히 클라이언트 개발에서 질리도록 쓰게 될텐데요,
???: 벡터 내적에 대해 아는대로 말해보세요.
면접 중에 이런 질문을 받는다면 어떻게 대답하실 건가요?
벡터 내적의 3가지 활용법에 대해 아주 간단히 알아보겠습니다.
램버트 코사인 법칙
램버트 코사인 법칙이란?
두 벡터의 내적은 각 두 벡터 길이, 그 사잇각의 코사인을 곱한 것과 같다는 법칙입니다.
어떻게 활용하는지에 대한 글이므로 왜 그렇게 되는지는 다루지 않겠습니다.
이 글에서 소개할 세 가지 방법은 모두 램버트 코사인 법칙을 이용합니다.
모두 단위벡터 →
램버트 코사인 법칙을 활용하라면 가장 먼저 떠올릴 수 있을 방법입니다.
이 되기 때문에 acos를 통해 각도를 구할 수 있습니다.
코사인을 구할 때 방향벡터가 있다면 초월함수라서 엄청 느린 코사인을 대신할 수도 있죠.
길이를 모름 → 앞뒷면 판별
코사인은 -90°에서 90°까지는 양수, 그 외에는 음수가 됩니다.
벡터의 길이는 음수가 될 수 없기 때문에 내적에서 부호는 코사인만이 결정할 수 있습니다.
어떤 면의 접선과 뷰 벡터를 내적한 결과가 음수라면 그 면은 뒷면입니다.
하나만 단위벡터 → 수선의 발 길이
위의 두 경우보다는 활용이 드문 경우입니다.
특정 벡터의 주어진 방향에 대한 수선의 발의 길이를 구할 때에도 활용할 수 있습니다.
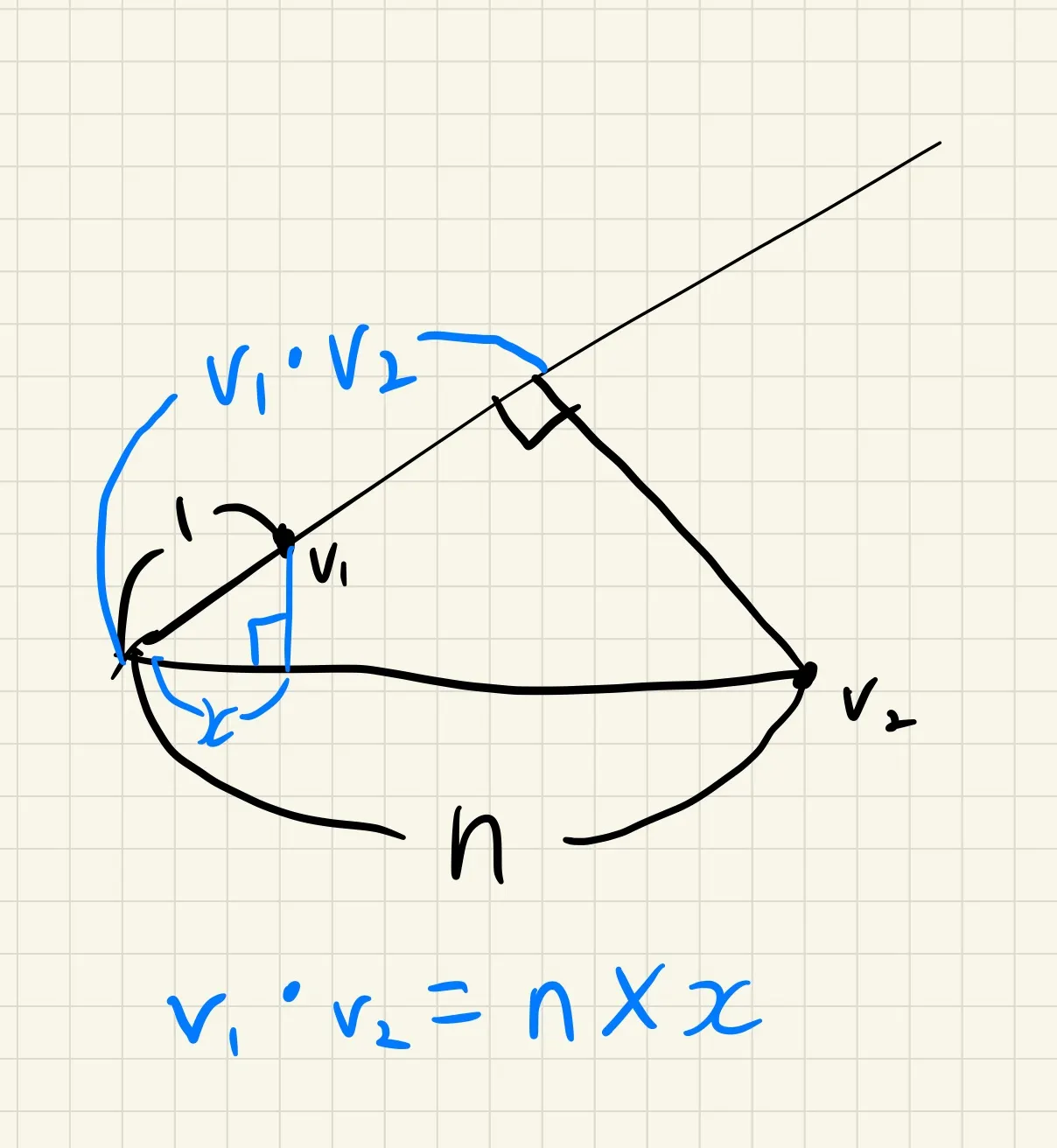
설명은 사진으로 대체하겠습니다. 다크모드 쓰시는 분들께는 눈뽕 죄송
벡터 내적으로 방향에 내린 의 수선의 발을 구하는 과정 (램버트 코사인 법칙, 삼각형의 닮음 활용)