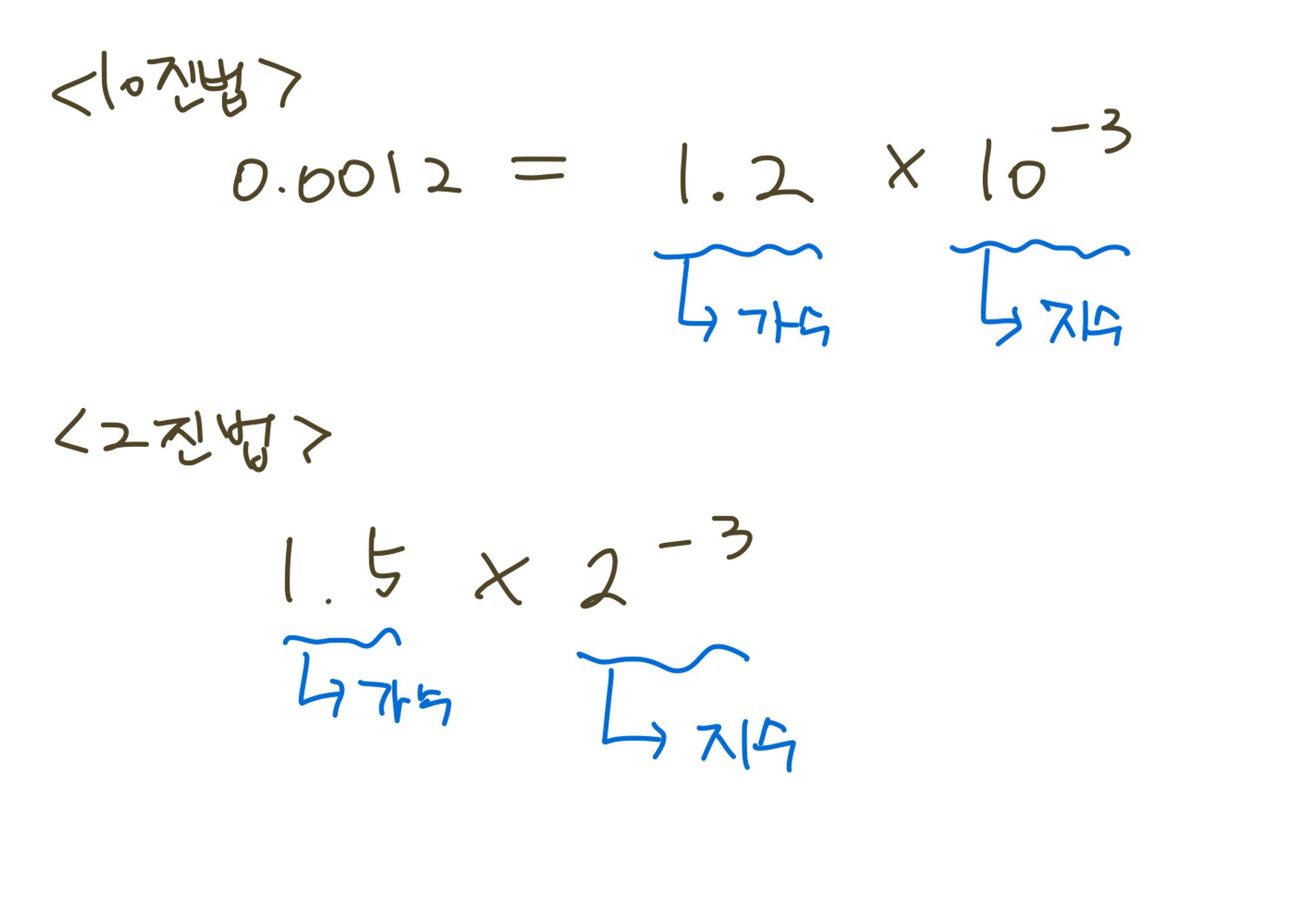고정표현법 (fixed point)
고정표현법 (fixed point)
실수는 고정표현법과 부동표현법 두 가지 방법으로 표현할 수 있다.
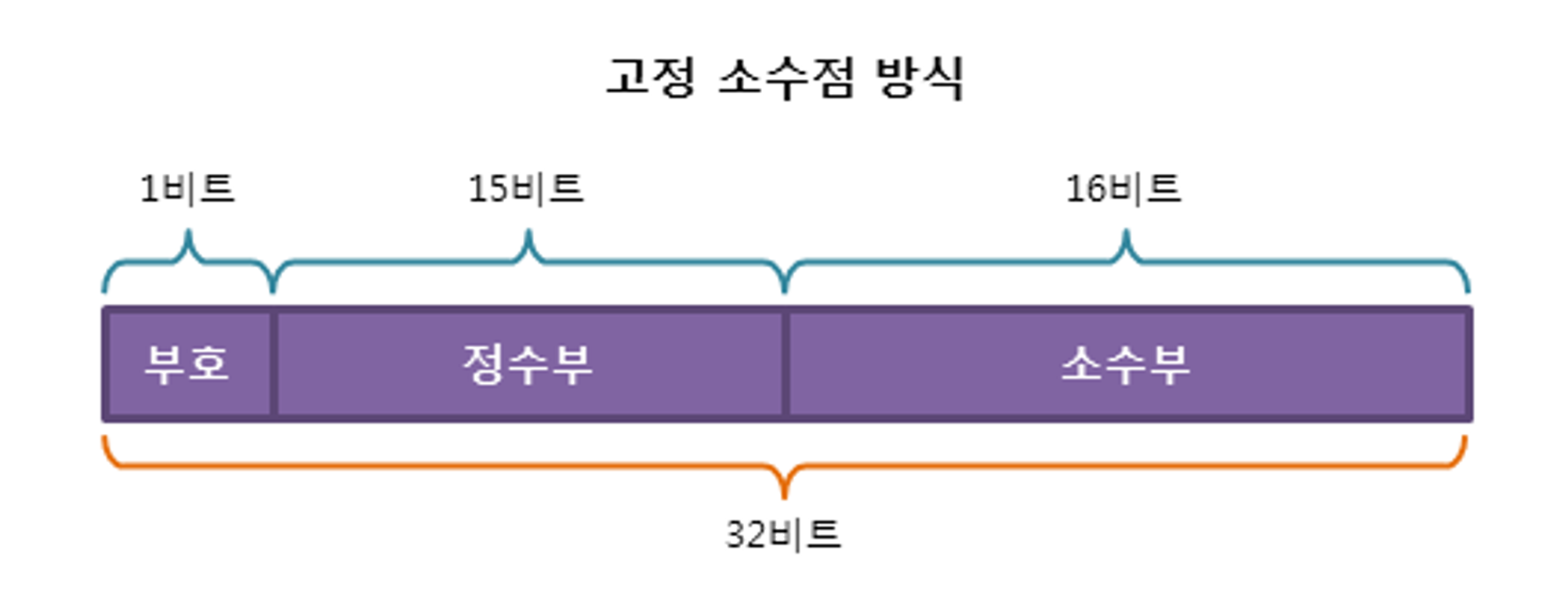
고정표현법은 실수를 정수부와 소수부로 나누고 소수부의 자릿수를 미리 정하여 고정된 자릿수의 소수를 표현하는 방식이다. 예를 들어 5비트가 있으면 제일 첫번째 비트는 부호를, 앞 쪽 2비트는 정수를 뒷 쪽 2비트는 실수를 표현하기로 정해놓는 것이다.
이 방법은 잘 작동하긴 하지만 많은 양의 수를 표현하기 어려워 범용 컴퓨터에서는 잘 사용하지 않는다.
 부동표현법 (floating point)
부동표현법 (floating point)
: 실수를 가수부와 지수부로 나누어서 표현하는 방식이다.지수의 크기에 따라 소수점의 위치가 이동되므로 부동표현법(floating point)라는 이름이 붙었다.가수부는 소수점 왼쪽이 한 자리 뿐인 소수를 의미하고, 지수부는 소숫점을 표현하는 10의 거듭제곱을 의미한다.예를 들어 0.0012는 1.2 * 10⁻³으로 표현할 수 있다.2진법으로 표기하려면 지수부분을 2를 밑으로하는 수로 표현하면 된다.
 IEEE 부동 소수점 방식
IEEE 부동 소수점 방식
부동표현법은 불편한 점은 많지만 일반적인 컴퓨터에서 소수를 표현할 때 채택하는 방식이다. 부동표현법을 더 정밀하게 사용하기 위해 IEEE 754라는 표준법을 따른다.IEEE표준법은 정밀도를 높이기 위해 몇 가지 방법을 사용한다.
•
정규화: 가수를 조정하여 맨 앞(왼쪽)에 0이 없게 만드는 것이다.
•
맨 왼쪽 비트 생략하기: 맨 왼쪽 비트는 항상 1이므로 1을 생략하고 사용한다. 이로 인해 가수에 1비트를 더 사용할 수 있다.
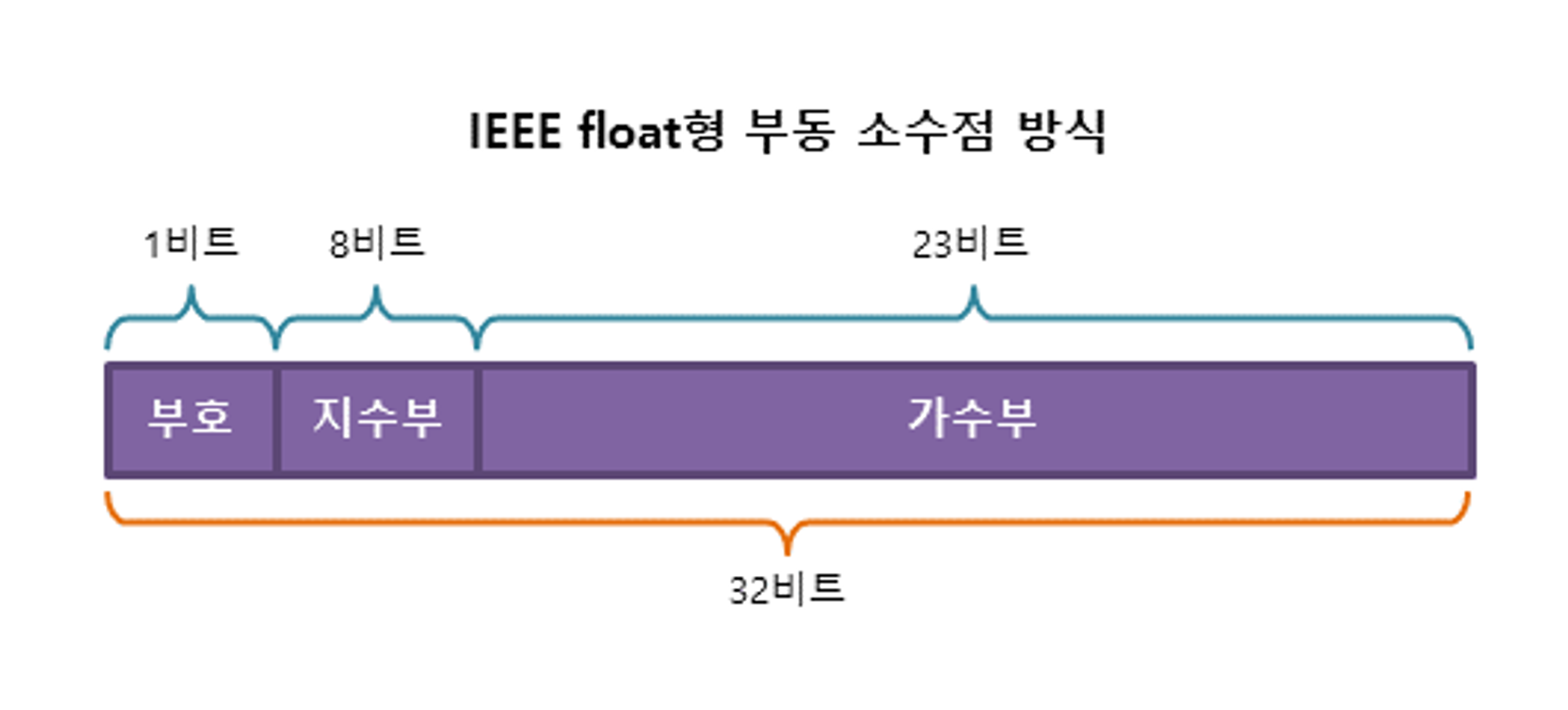
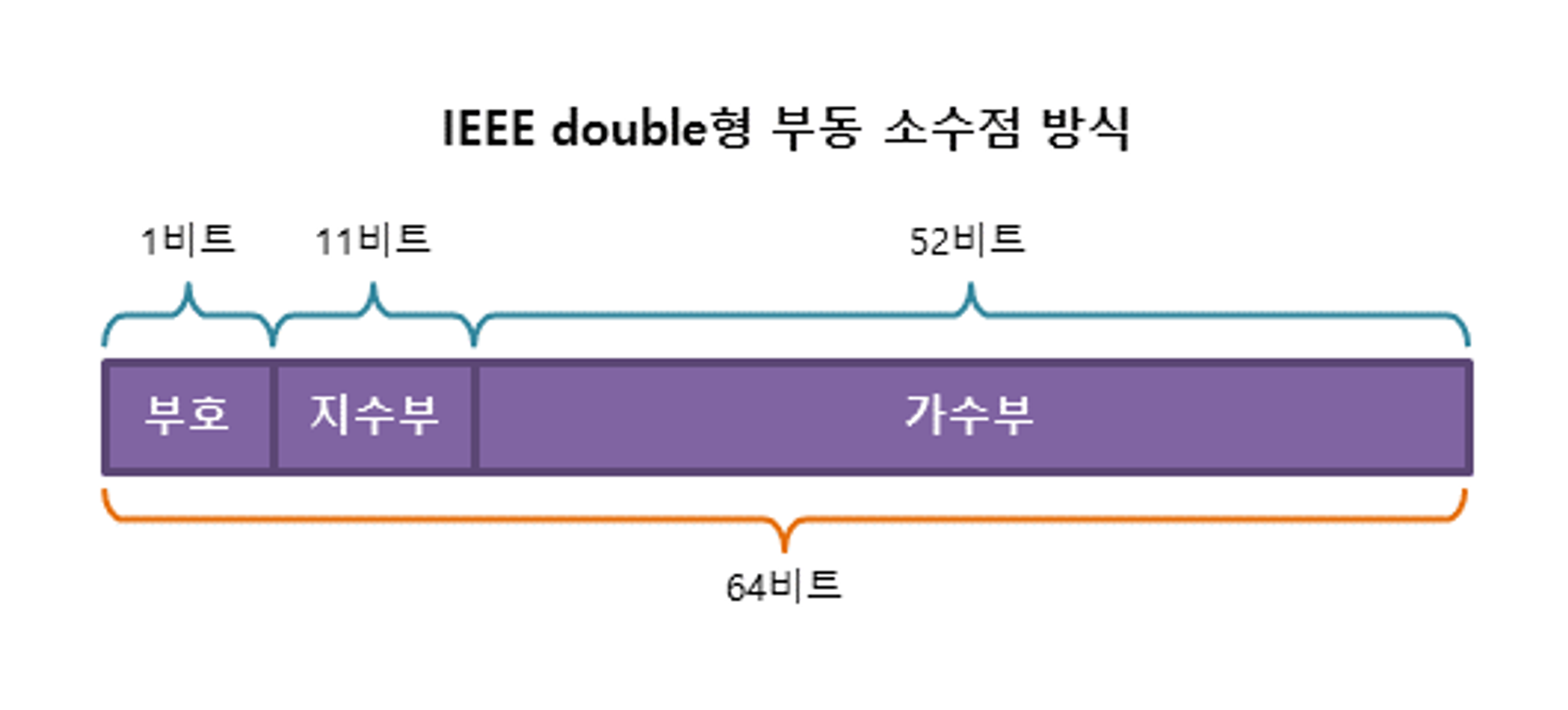
부동소수점은 두 가지 수를 많이 사용한다. 32비트의 float형 실수는 기본정밀도 부동소수점 수를 사용하고 64비트의 double형 실수는 2배 정밀도 부동소수점 수를 사용한다.
이름처럼 2배 정밀도수가 기본 정밀도수보다 정밀도도 높고 표현하는 수도 많다.