Subject
풀이
검증
1. 풀이
42 school의 push swap 과제의 3분할 퀵정렬 풀이입니다. 풀이 과정을 바탕으로 점화식을 유도하고, 3분할 퀵정렬에 대한 커맨드 개수를 수식으로 표현합니다. 또한 해당 풀이의 최악의 경우를 보이는 것으로 문제에서 주어진 조건을 항상 만족함을 보입니다.
1) 점화식 유도.
push swap과제의 커맨드 개수를 계산하기 위해서 점화식 A(n)과 B(n)을 다음과 같이 정의합니다.
•
A(n) 유도.
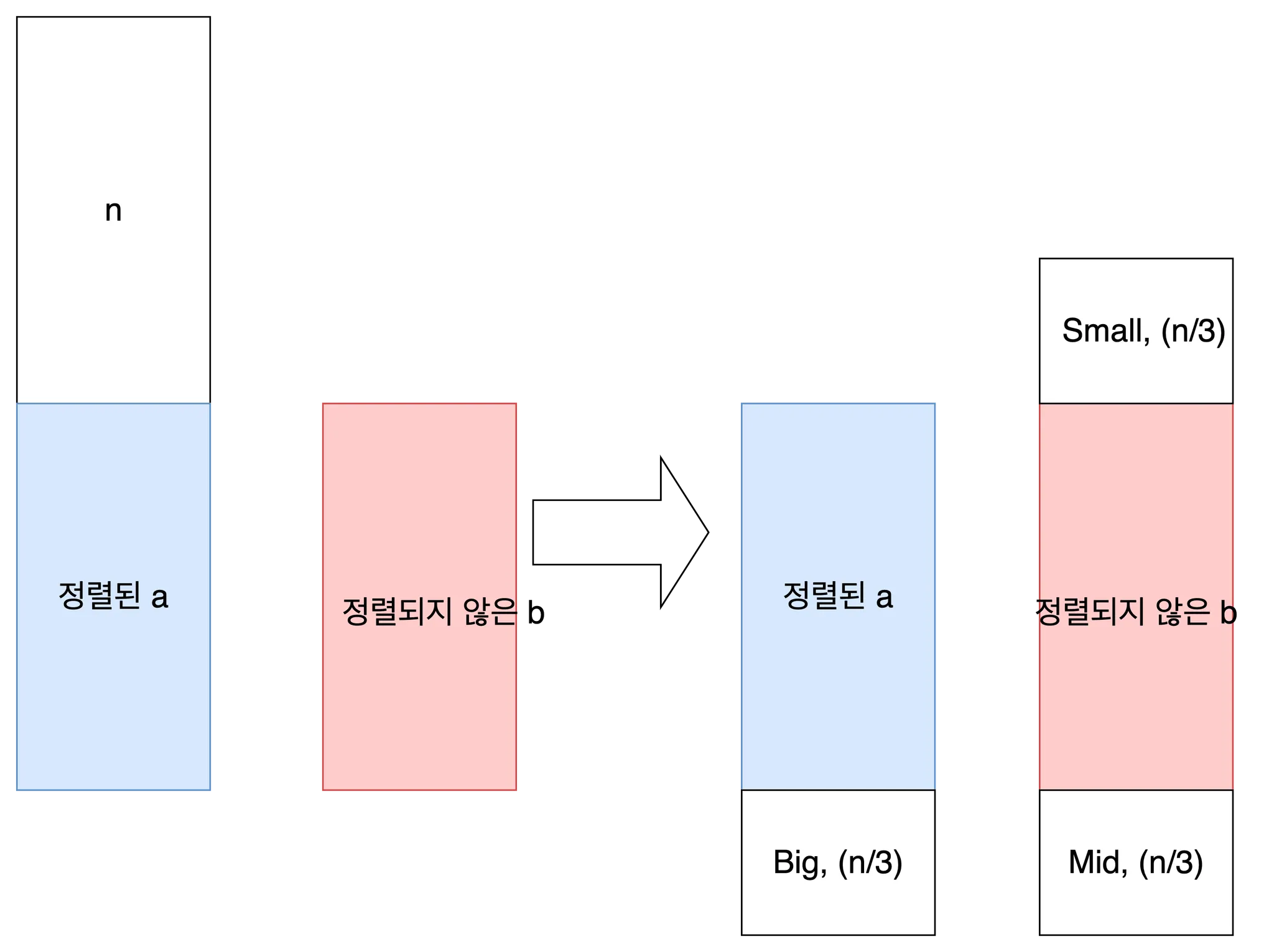
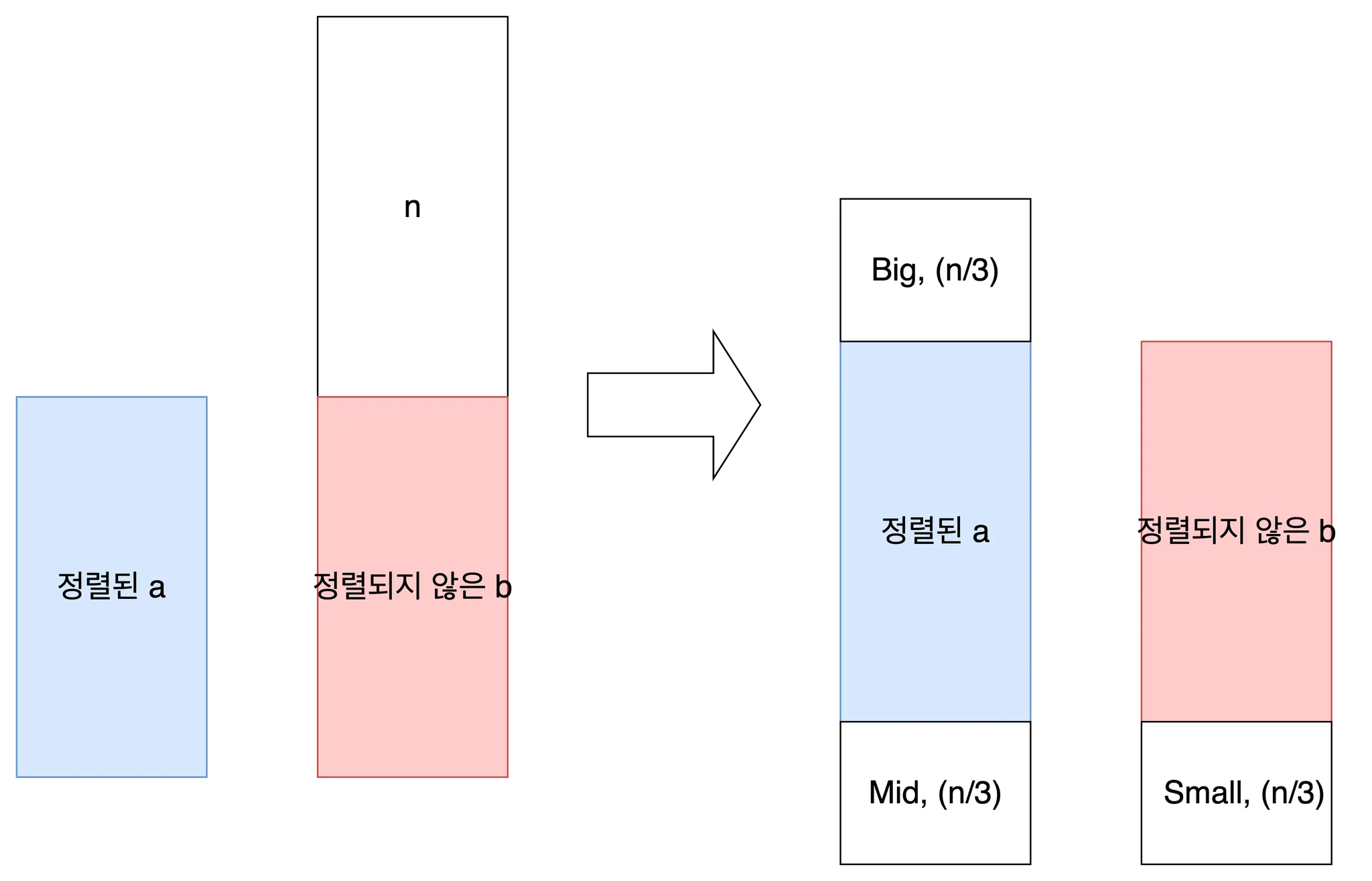
스택 a의 상단 n개 원소를 다음과 같이 3개의 파티션으로 분할합니다. 이 때 분할의 기준이 되는 두 pivot값은 입력 원소를 0~n-1로 정규화 하는 것으로 쉽게 획득할 수 있습니다.
두 pivot값을 기준으로 얻은 3개의 파티션에 대하여 가장 큰 값들을 Big, 두 pivot값 사이의 값들을 Mid, 가장 작은 값들을 Small이라 하겠습니다. 각각의 파티션은 정렬되지 않았으며, 그 크기는 n/3으로 가능한 동일하게 유지합니다.
Big파트는 ra, Small파트는 pb, Mid파트는 pb + rb 커맨드가 필요합니다. 각 파티션의 크기가 n/3이므로, 도합 4n/3개의 커맨드가 필요합니다.
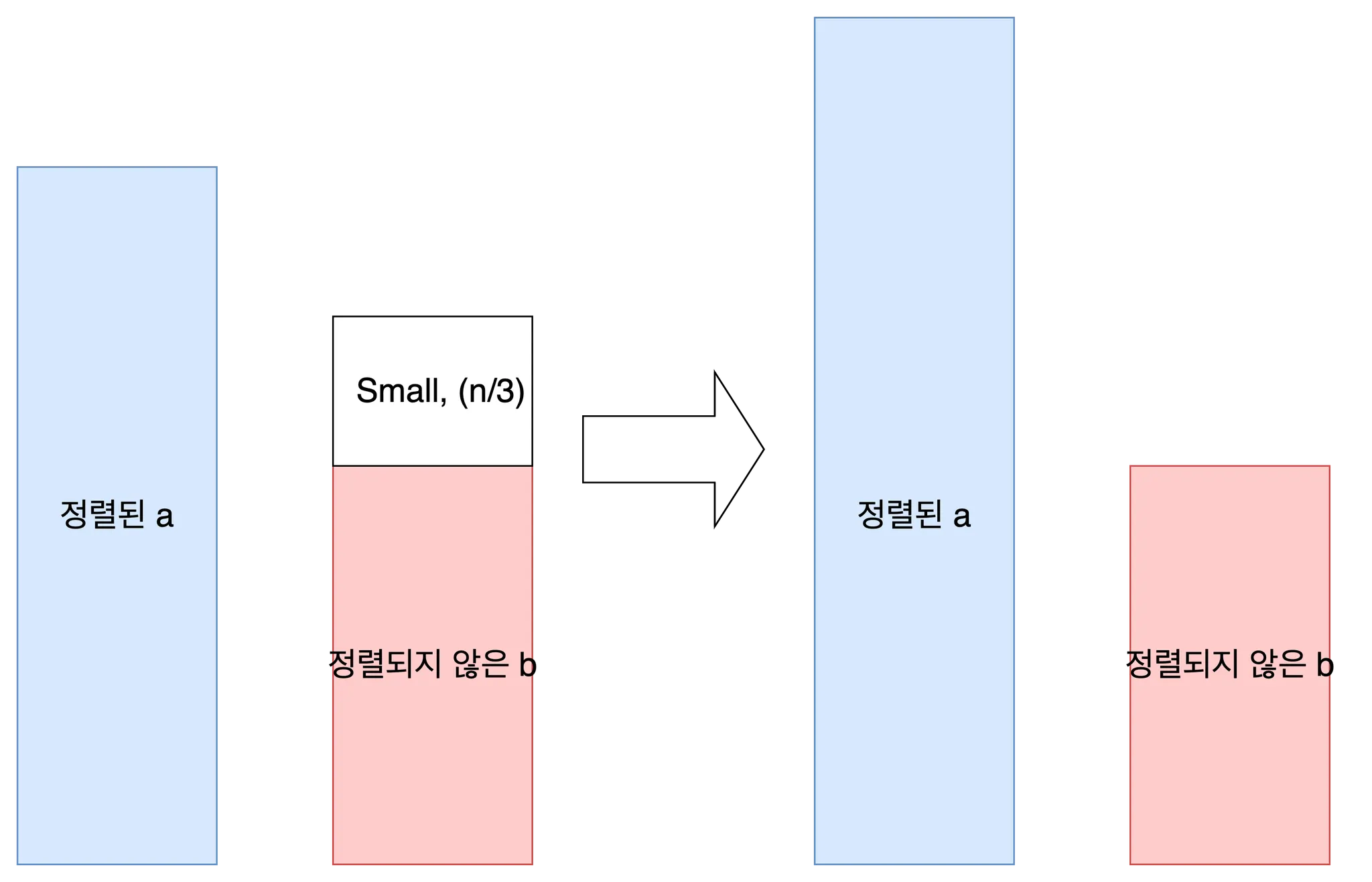
이 상황에서 rrr커맨드를 사용하여 Big과 Mid를 두 스택의 상단으로 한 번에 옮겨줍니다. 실제 상황에서는 n이 3의 배수가 아닐 수 있으므로, 위해서 Big과 Mid의 개수를 동일하게 맞춰줍니다.
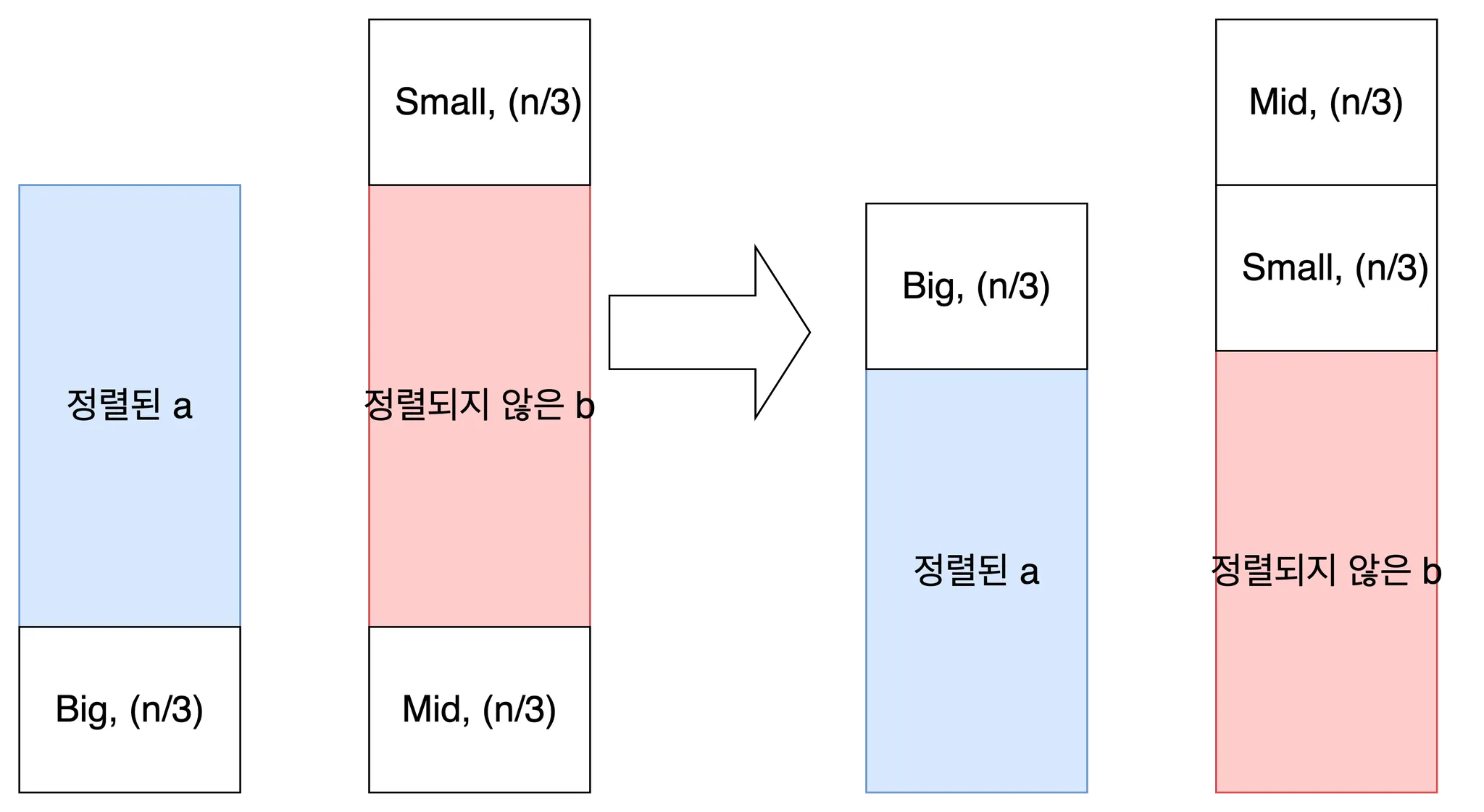
도합 n/3개의 원소에 대하여 rrr을 수행했으므로, 그 비용은 n/3입니다.
여기서 a의 상단에 위치한 Big에 대하여 재귀적으로 정렬을 수행합니다. Big은 a상단에 n/3개 만큼 위치하므로, 그 비용은 A(n/3)입니다.
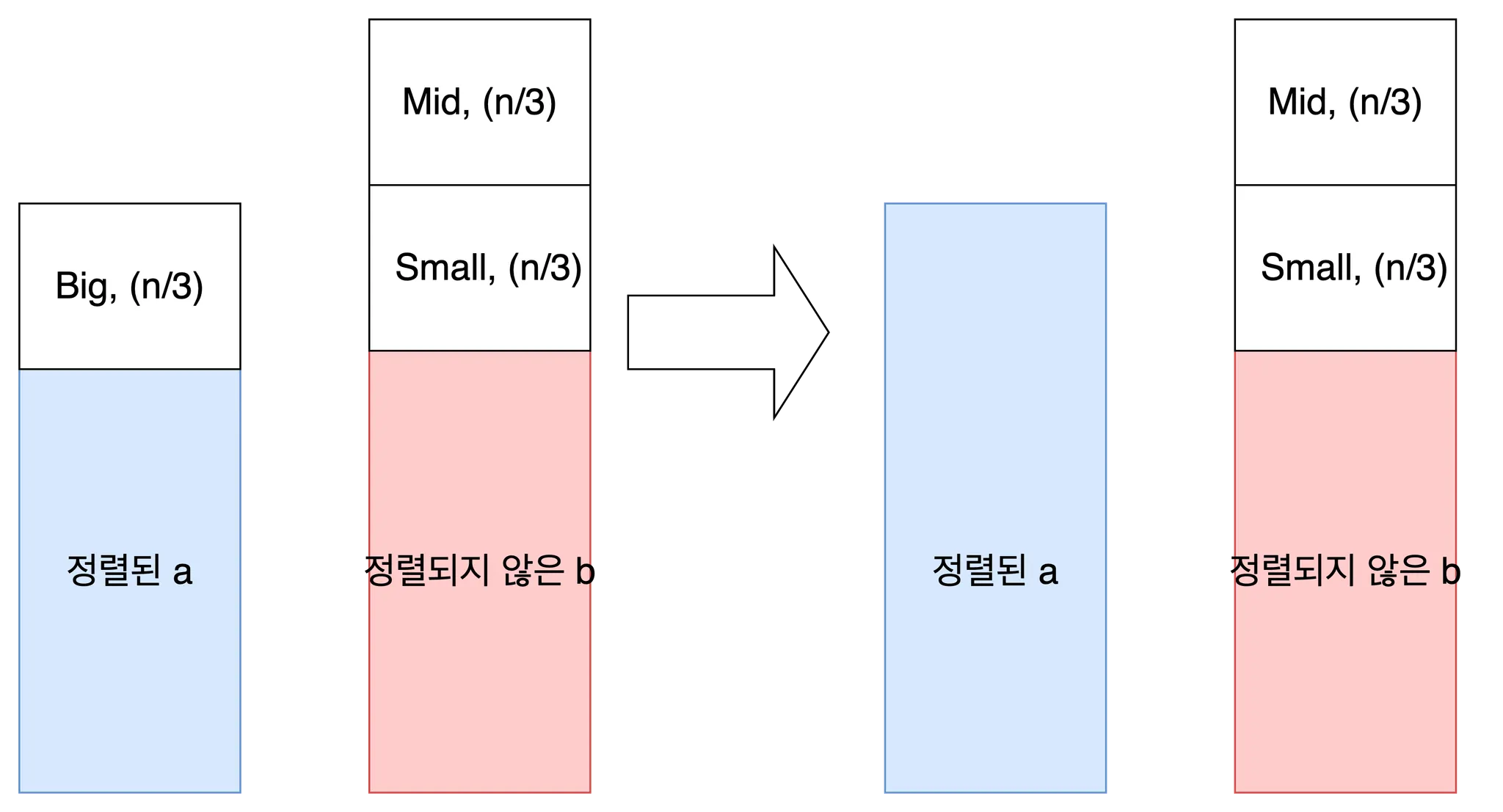
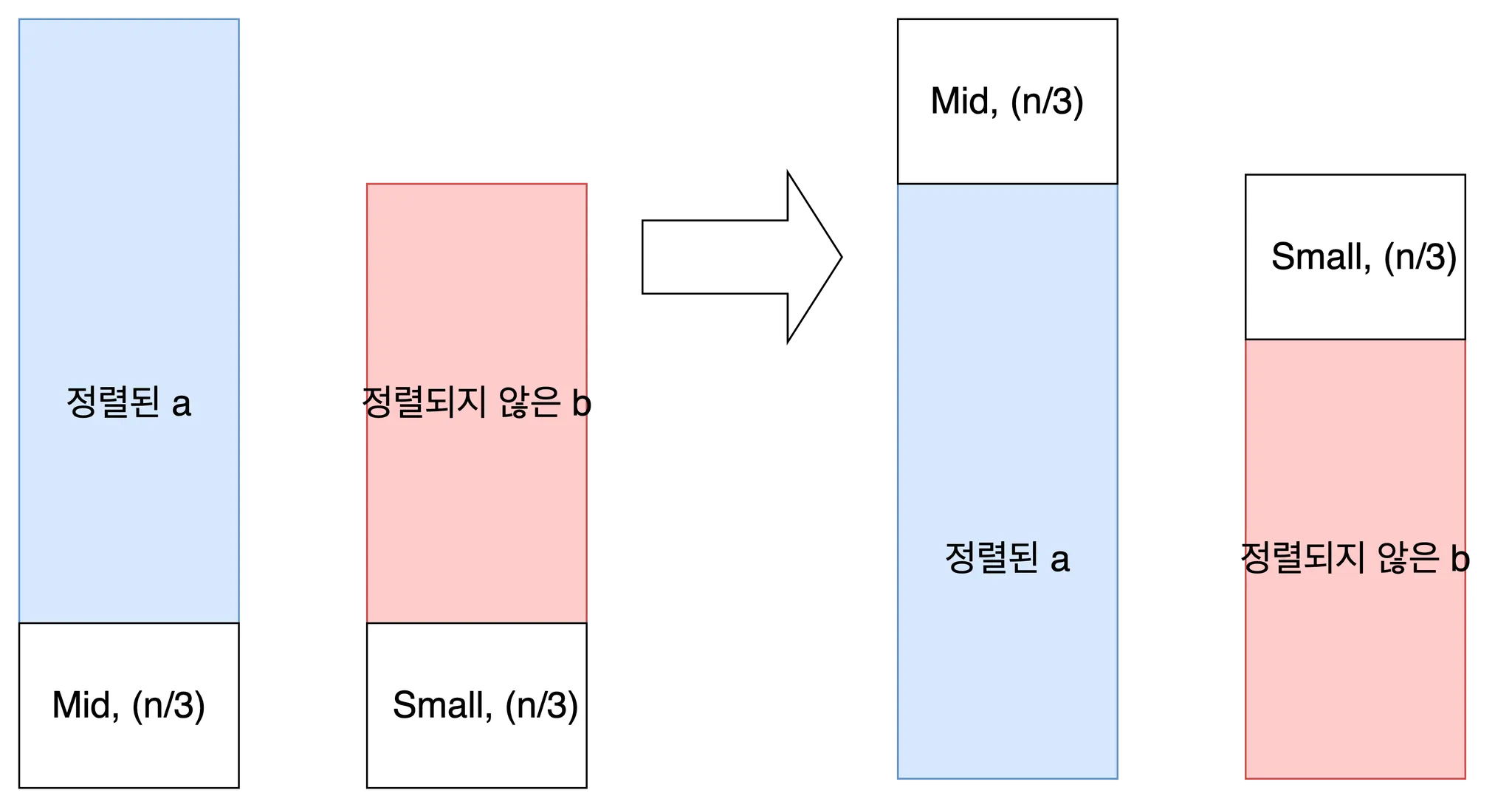
Mid에 대하여 재귀적으로 정렬하여 a의 상단으로 옮깁니다. Mid는 b의 상단에 n/3개만큼 존재하므로 그 비용은 B(n/3)입니다.
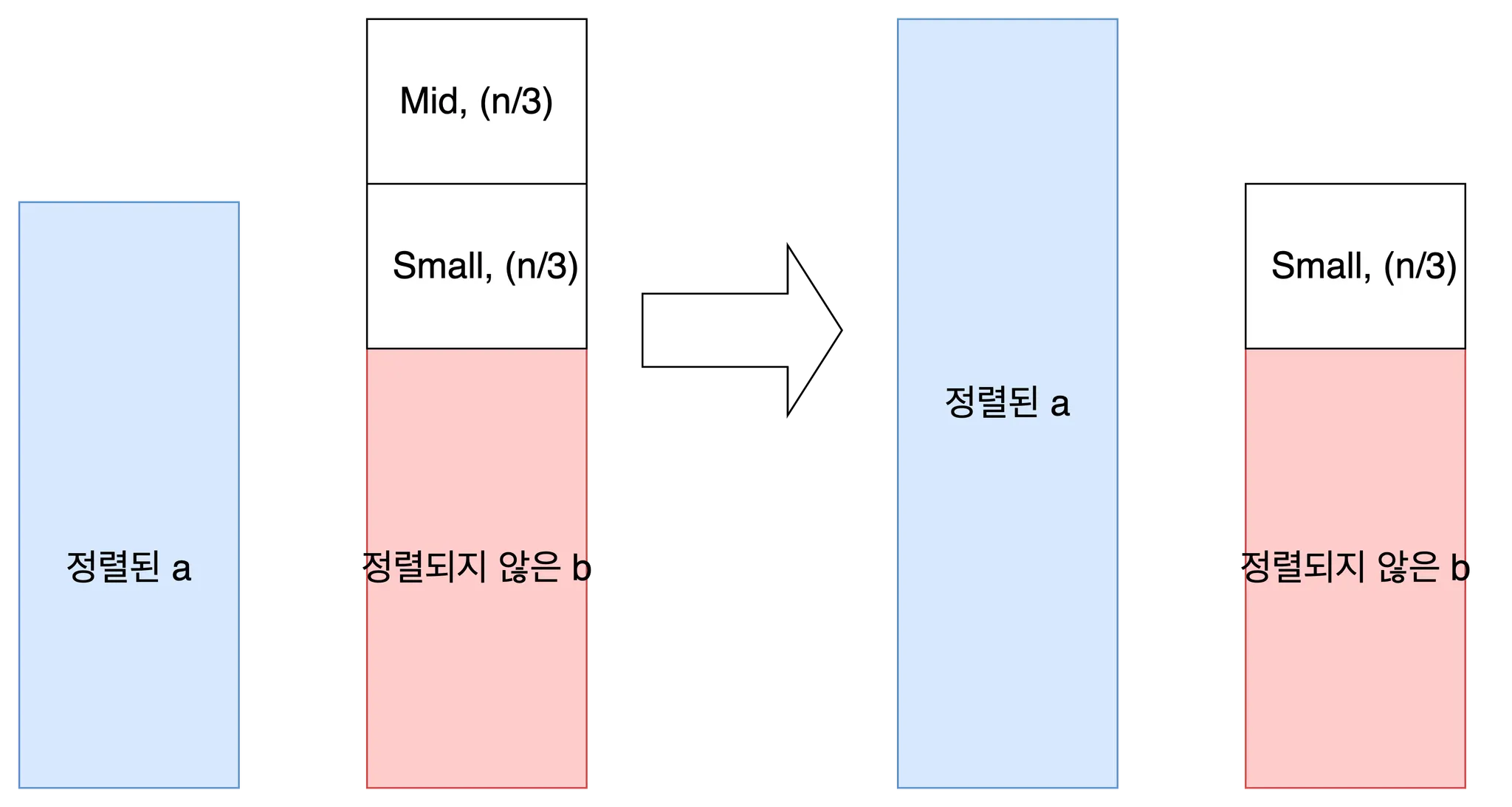
Mid와 마찬가지로 Small에 대해서도 재귀적으로 정렬 및 이동을 수행합니다. 비용은 B(n/3).
이상으로 a상단 n개 원소에 대한 정렬이 종료되었습니다. 각 과정을 거치면서 드는 비용을 총합하여 점화식 A(n)을 구하면 다음과 같습니다.
•
B(n) 유도.
A(n)과 유사하게 B(n)은 다음과 같이 수행됩니다.
3개의 파티션으로 분할, 그 비용은 4n/3.
Big 정렬, 비용은 A(n/3)
rrr커맨드를 이용하여 Mid와 Small 한 번에 상단으로 이동, 그 비용은 n/3.
Mid 정렬, 비용은 A(n/3)
Small을 정렬해서 a로 이동, 비용은 B(n/3)
이렇게 b의 상단의 n개 원소를 정렬하여 a의 상단으로 이동시켰습니다. 앞서 거친 단계들을 종합하면 다음과 같이 점화식을 얻을 수 있습니다.
2) 점화식 풀이.
3분할 퀵정렬에 대한 점화식은 다음과 같습니다.
두 점화식 사이에 대칭성이 존재하므로, 이 점을 이용하여 임의로 A(n)과 B(n)을 같다고 두고 풀 수 있습니다. 그 결과는 다음과 같습니다.
우변의 A(n/3)을 계속 전개합니다. 전개 가능한 횟수는 n이 더 이상 나눠질 수 없을 때 까지 이므로, 그 횟수는 log3(n)회 전개할 수 있습니다. 그 결과는 다음과 같습니다.
A(1)은 a상단의 1개 원소를 정렬하는 데에 드는 비용입니다. 하지만 이 상황은 정렬할 필요가 없으므로, A(1)의 값은 0입니다. 따라서 A(n)은 다음과 같습니다.
위 식은 우리가 필요로 하는 정확한 커맨드 개수를 의미하지는 않습니다. 일단 A(n)과 B(n)이 같지 않기 때문이며, n이 정수이므로 3분할 불가능한 경우가 항상 1로 떨어지지도 않기 때문입니다. 따라서 추가적인 생각이 필요합니다. 위 식의 진정한 의미는 Big O 표기법에 있습니다. A(n)의 가장 dominant한 항이 5n log3(n)이므로, Big O 표기법에 의해서 해당 알고리즘의 복잡도는 O(n log n)입니다.
3) 공식 해석.
우리가 필요로하는 실제 커맨드 개수를 구하기 위해서 앞서 구한 두 점화식에 대해서 다시 한 번 생각해봅시다. A(n)과 B(n)모두 n개의 원소를 한 번 3분할하는데 5n/3개의 커맨드를 소모하며, 나머지 3개의 파티션은 그 위치에 따라서 각자의 비용을 필요로 합니다. 이 점을 바탕으로 실제 A(n)을 구하면 다음과 같습니다.
5/3이 a의 top에 위치한 원소가 분할되기 위한 비용의 기대값이라는 점을 바탕으로 여기서 한 번 더 일반화를 수행할 수 있습니다. 이를 통해서 우리는 push swap과제에 대하여 임의의 분할로 quick정렬을 수행할 때 드는 비용의 식을 얻을 수 있습니다.
2. 검증
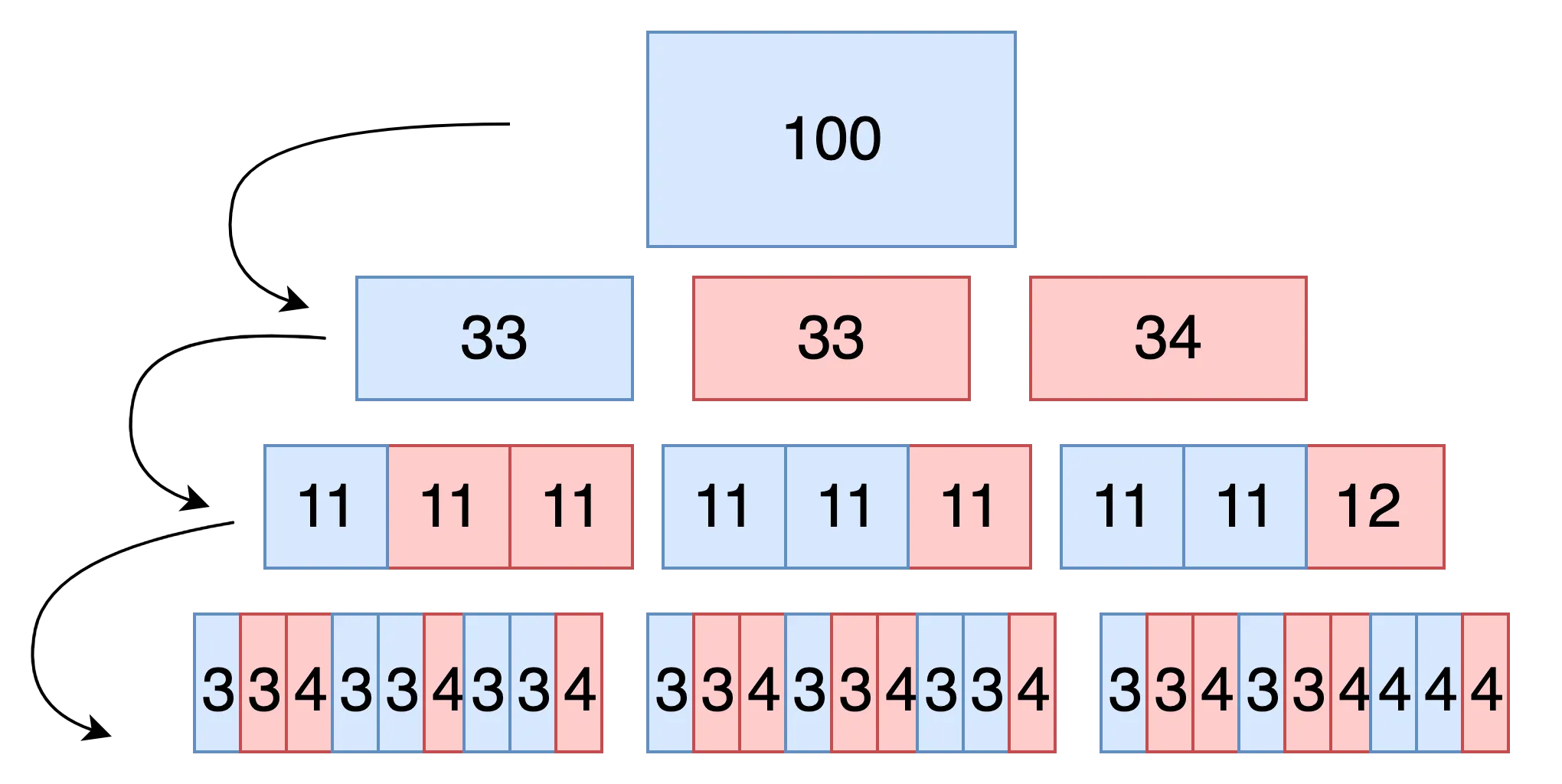
a에 입력된 원소가 100개인 경우, 앞서 구한 공식을 적용하고 최악의 경우 몇개의 커맨드가 필요한지 알아봅시다. 아래는 3분할 퀵정렬을 수행한 과정을 나타낸 결과입니다. 파란 색은 A, 붉은 색은 B를 의미합니다.
각 base case의 최대 값은 다음과 같습니다. 해당 base case의 값들은 하드 코딩을 통해서 상황별 최적의 정렬 방법을 구현한 결과입니다.
또한 여기서 최초의 3분할에 대해서는 n/3개 만큼의 rrr을 생략 가능한 점을 추가적으로 고려하면, 추가적으로 n/3개의 커맨드를 아낄 수 있습니다.
따라서 100개 정수에 대해서 push swap을 수행한 결과, 최악의 경우 673개의 command가 필요함을 확인했습니다. 이는 곧 문제의 조건인 700개를 항상 만족함을 의미합니다. 마찬가지 방식으로 500개의 경우에 대해서도 커맨드 개수의 최대값을 구할 수 있지만 여백이 부족하여 생략합니다. 특히 n log n 복잡도를 갖는 알고리즘의 특성 상, n의 값이 커질수록 상대적인 성능이 올라가기에 굳이 확인할 필요가 없을 것으로 생각됩니다.
이같은 과정을 통해서 n=3, n=4에 대한 경우와 최초의 3분할에 대해서 추가적인 최적화를 필요로 하기는 하지만, 3분할 quick정렬은 최악의 경우에 대해서도 문제의 조건을 반드시 만족함을 증명했습다.
Thanks to.
push swap의 퀵정렬 풀이에 도움을 주신 42서울의 jijeong님, 비록 잘 알진 못하지만 커맨드 개수 분석 방법에 대해서 영감을 주신 42서울의 hyunjunl님, 풀이의 수학적인 부분을 검수해주신 김영찬(ch96an)님 감사합니다.