summary
inspired by the world-famous Wolfenstein 3D game, which was the first FPS ever. It will enable you to explore ray-casting. Your goal will be to make a dynamic view inside a maze, in which you’ll have to find your way.
what is ray-casting?
Raycasting is a rendering technique to create a 3D perspective in a 2D map. Back when computers were slower it wasn’t possible to run real 3D engines in realtine, and raycasting was the first solution. Raycasting can go very fast, because only a calculation has to be done for every vertical line of the screen
The basic idea
The basic idea of raycasting is as follow: the map is a 2D square grid, and each square can either be 0 (no wall), or a positive value (= a wall with a certain color or texture).
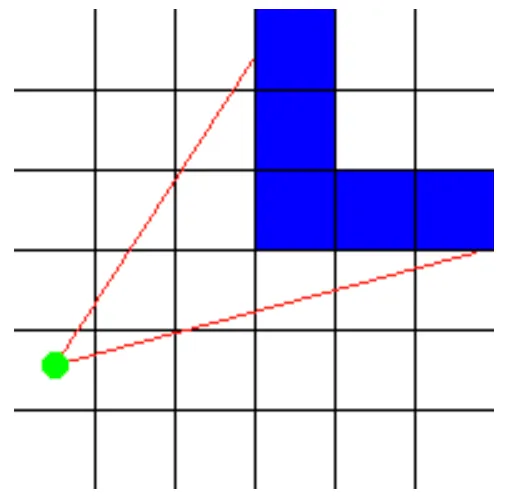
For every x of the screen (for every vertical stripe of the screen), send out a ray that starts at the player location and with a direction that depends on both the player’s looking direction, and the x-coordinate of the screen. Then, let this ray move forward on the 2D map, until it hits a map square that is a wall. if it hit a wall, calculate the distance of this hit point to the player, and use this distance to calculate how this wall has to be drawn on the screen: the further away the wall, the smaller it’s on screen, and the closer, the higher it appers to be. These are all 2D calculations. This image shows a top down overview of two such rays(red) that start at the player (green dot) and hit blue walls
To find the first wall that a ray encounters on its way, you have to let it start at the player’s position, and then all the time, check whether or not the ray is inside a wall. if it’s inside a wall, then the loop can stop, caculate the distance, and draw the with the correct height. if the ray position is not in a wall, you have to trace it further: add a certain value to its position, in the direction of the direction of this ray, and for this new position, again check if it’s inside a wall or not, Keep doing this untill finally a wall is hit.
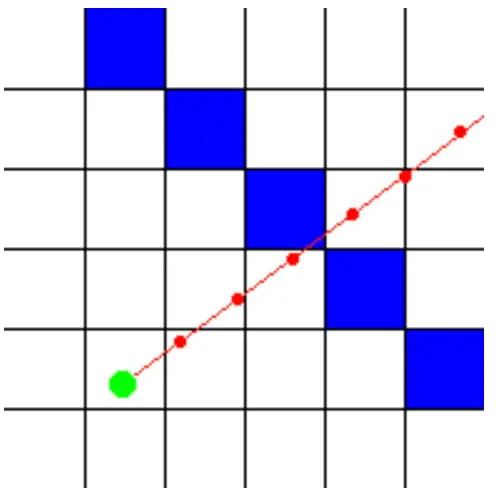
A human can immediatly see where the ray hits the wall, but it’s impossible to find square the ray hits immediatly with a single formula, because a computer can only check a finite number of position on the ray. Many raycasters add a constant value to the ray each step, but then there’s a chance that it may miss a wall! For example, with this red ray, its position was cheked at every red spot.
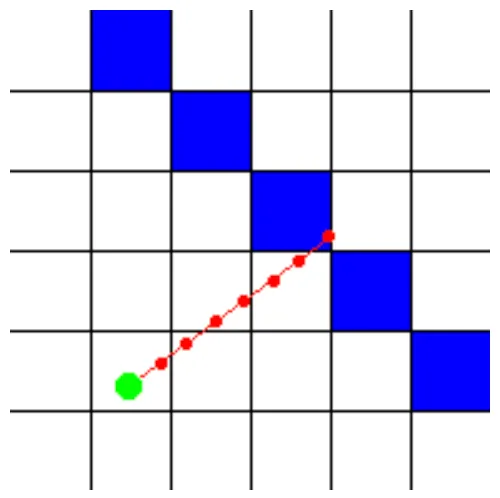
As you can see, the ray goes straight through the blue wall, but the computer didn’t detect this, because it only checked at the positions with the red dots. The more position you check, the smaleer the chance that the computer won’t detect a wall, but the more calculations are needed. Here the step distance was halved, so now he detects that the ray went through a wall, though the position isn’t completly correct.
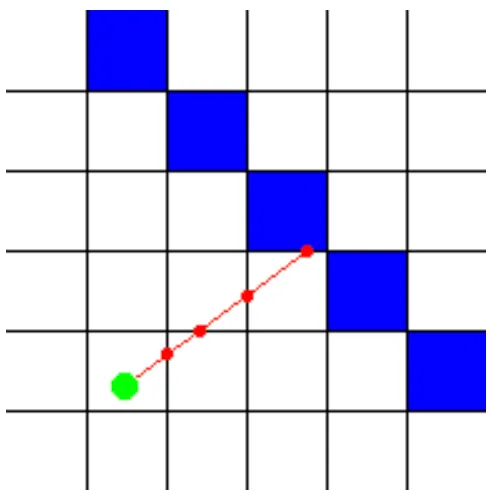
For infinite precision with this method, an infinitely small step size, and thus an infinite number of calculations would be needed! That’s pretty bad, but luckily, there’s a better method that requires only very few calculations and yet will detect every wall: the idea is to check at every side of a wall the ray will encounter. We give each square width 1, so each side of a wall is an integer value and the places in between have a value after the point. Now the step isn’t constant, it depends on the distance to next side
As you can see on the image above, the ray hits the wall exactly where we want it. In the way presented in this tutorial, an algorithm is used that’s based on DDA or “Digital Differential Analysis”. DDA is a fast algorithm typically used on square girds to find which squares a line hits (for example to draw line on a screen). So we can also use it to find which squares of the map our ray hits, and stop the algorithm once a square that is a wall is hit
*Euclidean angles: 일반적으로 우리가 생활에서 사용하는 일상적인 공간의 모델을 나타냅니다.
일부 ray-tracer는 유클리드 각도를 활용해 플레이어의 방향과 광선을 나타내며 시야를 결정하지만, 벡터와 카메라로 이 작업을 하는 것이 훨씬 쉽습니다. 우리는 다음의 방법으로 시야를 결정합니다.
•
플레이어의 위치는 항상 벡터 (x좌표, y좌표)입니다.
•
플레이어가 보는 방향은 방향벡터로 나타냅니다.
이렇게 벡터를 이용하는 방법에는 방향벡터 외에 카메라 평면도 필요합니다.
•
상단의 이미지에서 카메라 평면은 컴퓨터 화면의 표면을 나타냅니다.
•
방향벡터(black)는 화면 내부 쪽을 가리킵니다.
•
카메라평면은 항상 방향벡터에서 수직입니다.
•
점으로 표현되는 플레이어의 위치는 카메라 평면보다 앞에 있습니다.
•
화면에서 특정 x 좌표의 특정 광선은 이 플레이어의 위치에서 시작하여 화면의 해당 위치 또는 카메라 평면을 통과하는 광선입니다.
•
진짜 3D 엔진은 3차원을 다루므로 벡터 2개가 필요하지만, 2차원 맵을 다루는 레이캐스팅은 카메라평면이 진짜 평면이 아니고 선이므로 벡터 1개로 표시합니다.
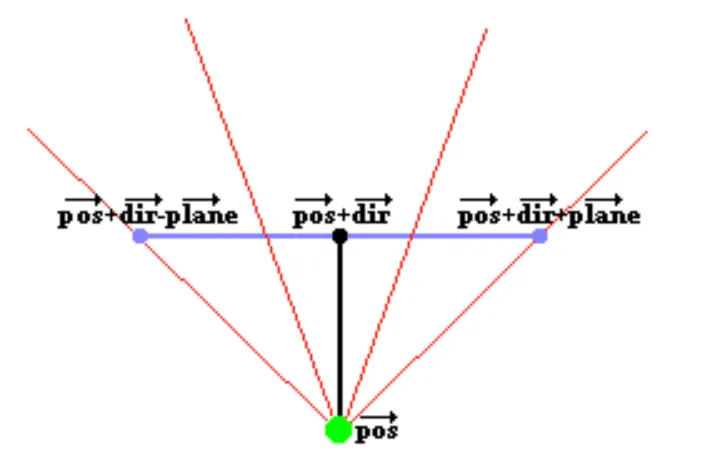
벡터의 덧셈을 이용해서 다음과 같이 필요한 벡터를 표현해보겠습니다.
•
pos 벡터: 플레이어의 위치 (green spot)
•
dir 벡터: 방향벡터 (black line)
•
plane 벡터: 전체 카메라 평면 중 박향벡터의 끝점으로부터 오른쪽 카메라평면의 끝점까지
•
방향벡터 끝점: pos + dir
•
오른쪽 카메라 평면의 끝점: pos+ dir + plane
•
왼쪽 카메라 평면의 끝점: pos+ dir - plane
이제 광선의 방향은 카메라평면으로부터 쉽게 구할 수 있습니다.
•
계산 방법은 (방향 벡터) + (카메라 평면 X 배수) 입니다.
•
예를 들어 위 이미지에서 적색 선은 광선을 나타내는데, 카메라 평면의 오른쪽에서 길이의 약 1/3 지점을 통과하는 세 번재 광선을 보겠습니다.
•
광선의 방향: dir + plane * 1/3
•
이 광선의 방향은 rayDir 벡터라고 하고, 벡터의 X, Y 값은 DDA 알고리즘에 사용됩니다
바깥쪽 선 두개는 스크린의 왼쪽/오른쪽 경계이고, 두 선 사이의 각도를 FOV (Field of View)라고 합니다.
•
FOV는 “방향 벡터의 길이 : 평면의 길이”의 비율로 결정됩니다.
•
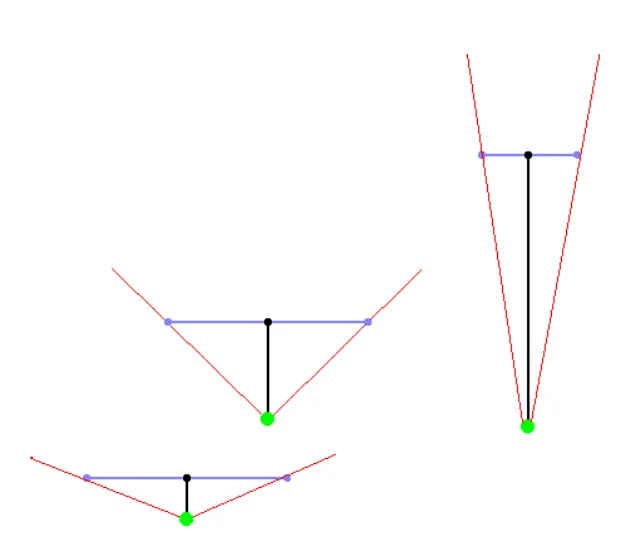
다른 FOV의 몇 가지 예는 다음과 같습니다.
◦
방향 벡터와 카메라 평면 벡터의 길이가 같은 경우, FOV는 90도 입니다.
▪
방향벡터 길이: 평면 길이 == 1 : 1
◦
방향 벡터가 카메라 평면보다 훨씬 길면 FOV가 90도 보다 훨씬 작아집니다.
▪
시야가 좁아져서 더 자세한 내용을 볼 수 있고 깊이가 줄어들므로 확대와 동일합니다.
▪
방향벡터 길이: 평면 길이 == LONG : 1
◦
방향 벡터가 카메라 평면보다 짧으면 FOV가 90도 보다 커집니다.
▪
방향 벡터가 0에 가까울 경우 180도가 최대입니다.
▪
축수와 같이 훨씬 넓은 시야를 갖게 됩니다.
▪
방향 벡터 길이 : 평면 길이 == 1 : LONG
•
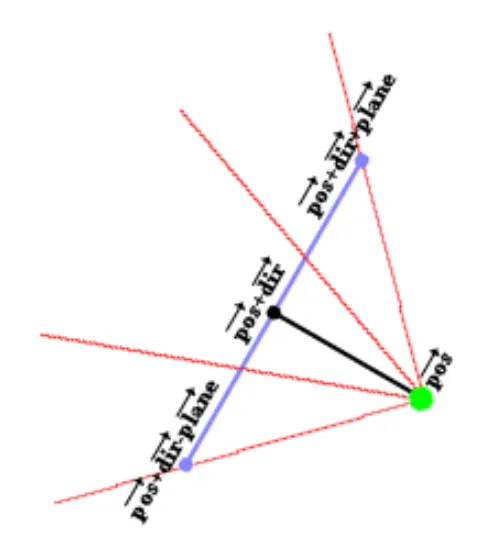
플레이어가 방향을 돌리면 시야가 따라서 회전해야 하므로 방향벡터와 카메라평면벡터가 모두 회전해야합니다.
◦
그러면 모든 광선도 따라서 회전시킬 수 있습니다.
◦
벡터를 회전 시키려면 회전행렬과 곱해주세요
▪
[cos (a) - sin (a)]
▪
[sin (a) - cos (a)]
Untextured Raycaster
DDA
// Perform DDA: 벽을 찾는 알고리즘
while (hit == 0)
{
if (sideDistX < sideDistY)
{
sideDistX += deltaDistX;
mapX += stepX;
side = 0;
}
else
{
sideDistY += deltaDistY;
mapY += stepY;
side = 1;
}
// Check if ray hit a wall
if (worldMap[mapX][mapY] > 0)
hit = 1;
}
C
복사
위 DDA 알고리즘은 ray를 한 칸씩 움직이며 벽에 부딪히는지 확인합니다.
•
반복할 때마다 stepX를 사용하며 x방향으로 한 칸 또는 stepY를 사용하여 y방향으로 한 칸 점프합니다.
•
만약 광선의 방향이 x축 방향과 완전히 일치한다면, x방향으로 한 칸씩 점프하면 됩니다.
•
만약 광선의 방향이 y축 방향과 완전히 일치한다면, y방향으로 한 칸씩 점프하면 됩니다.
•
광선이 점프할 때마다 sideDistX, sideDistY는 deltaDistX, deltaDistY가 더해지며 업데이트 됩니다.
•
광선이 점프할 때마다 mapX, mapY는 stepX, stepY가 더해지며 값이 업데이트 됩니다.
광선이 부딪히면 루프가 종료됩니다.
•
이 때, 변수 side의 값이 0이면 벽의 x면(x 축면, 세로 벽), 1이면 벽의 y면(y 축 면, 가로 벽)에 부딪혔다는 것을 알 수 있고, 또 mapX, mapY로 어떤 벽이랑 부딪힌 건지도 알 수 있습니다.
•
우리는 그 벽에서 정확히 어느 지점에서 부딪힌 건지는 알 수 없는데, 지금은 텍스쳐 없이 색상만 표현하기 때문에 몰라도 괜찮습니다.
광선의 시작점에서 벽까지의 이동거리 계산
벽을 만나 DDA가 완료되었으니 이제 광선의 시작점에서 벽까지의 이동거리를 계산하겠습니다.
•
이 거리는 나중에 벽을 얼마나 높게 그릴지를 알아내는데 사용됩니다.
•
어안렌즈 효과는 실제 거리 값을 사용했을 때, 모든 벽이 둥글게 보여서 회전할 때 울렁거릴 수도 있는 현상을 말합니다.
•
이러한 어안렌즈 효과를 피하기 위해, 플레이어 위치까지의 유클리드 거리 대신에, 카메라 평면까지의 거리를 사용할 것입니다.
•
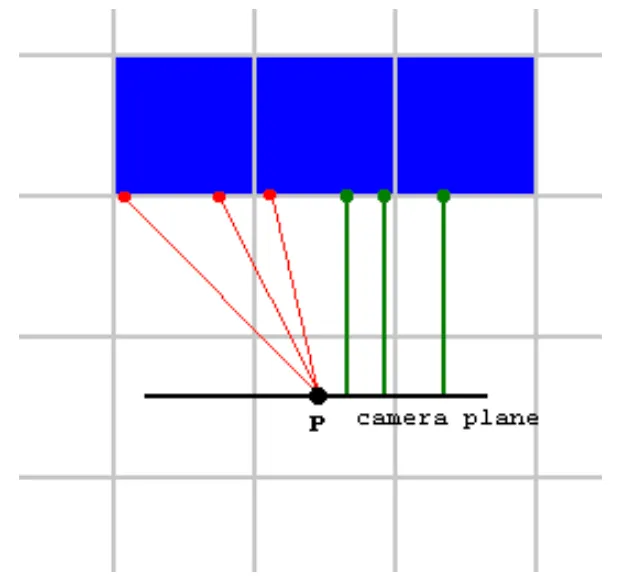
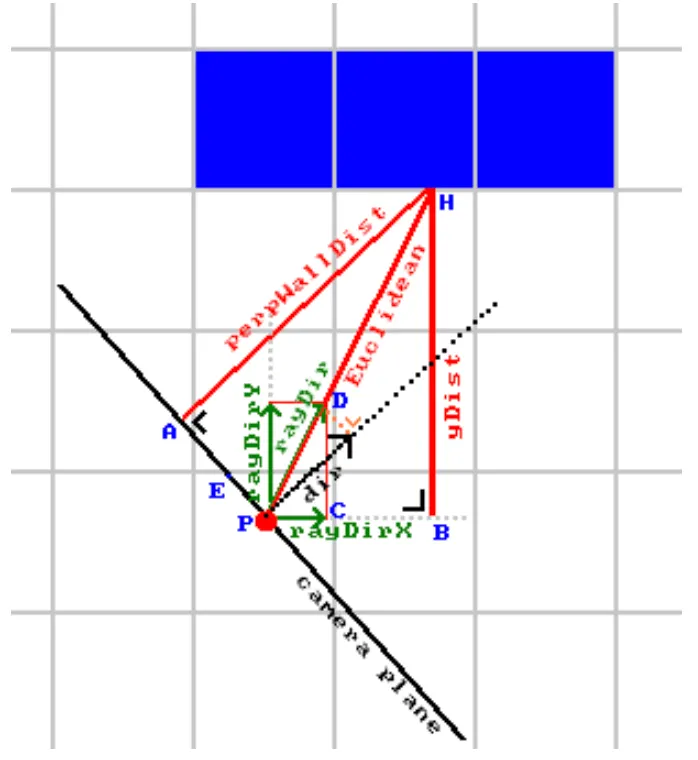
위의 이미지는 플레이어 대신 카메라 평면까지 거리를 사용하는 이유를 보여줍니다.
◦
적색 선은 벽의 적중지점에서 플레이어까지 유클리드 거리를 나타내는 광선을 나타냅니다.
◦
녹색 선은 벽의 적중지점에서 카메라 평면으로 바로 이동하는 광선을 나타냅니다.
◦
플레이어는 벽을 정면으로 보고 있어 벽의 윗선과 아랫선이 화면에서 수평을 이뤄야 합니다.
◦
적색 선의 길이를 적용하면, 적색 선의 길이가 다르기 때문에 벽의 높이가 일정하지 않아 결국 벽이 둥글게 보이게 되는 것입니다.
◦
반면에 오른쪽의 녹색 선은 모두 길이가 같아서 녹색 선을 적용하면 올바른 결과를 얻을 수 있습니다.
◦
플레이어가 회전할 때 (카메라 평면이 벽과 평면이 아니게 되고 녹색 선의 길이도 서로 달라지지만 서로 일정한 차이를 유지하면서 달라짐)에도 동일하게 적용되어 벽은 화면에 대각선이긴 하지만 직선으로 보이게 됩니다.
◦
이 설명은 완벽하지는 않지만 어느 정도의 이해를 돕습니다.
// Calculate distance projected on camera direction
// Euclidean distance will give fisheye effect!
if (side == 0)
perpWallDist = (mapX - posX + (1 - stepX) / 2) / rayDirX;
else
perpWallDist = (mapY - posY + (1 - stepY) / 2) / rayDirY;
C
복사
•
여기서 사용하는 레이캐스팅 방법은 광선의 이동거리를 계산하면서, 어안렌즈 효과를 보정하는 코드를 따로 추가하지 않고도 간단히 방지할 수 있는 방법입니다.
◦
이 수직거리를 구하는 방식은 실제 이동거리를 구하는 방식보다 훨씬 쉽고, 벽에 어느 위치에 정확히 부딪혔는지 몰라도 구할 수 있습니다.
◦
위의 예제코드에서, (1 - stepX) / 2 는 stepX가 -1 이면 1, stepX가 1이면 0이 됩니다. 이는 rayDirX < 0 일 때 길이에 1을 더해주기 위한 코드입니다.
•
수직 거리를 계산하는 방법은 다음과 같습니다.
◦
만약 광선이 처음으로 부딪힌 면이 x면이라면, mapX - posX + (1 - stepX) / 2 는 광선이 x 방향으로 얼마나 갔는지를 나타내는 수식입니다. (정수일 필요 없음)
◦
만약 광선의 방향이 x면에 수직이면 이미 수직거리의 값이지만 대부분의 경우 광선의 방향이 있고 이 때 구해진 값은 실제 수직거리보다 큰 값이므로 rayDirX로 나누어줍니다.
◦
y면에 부딪힌 경우에도 같은 방식으로 계산해줍니다.
◦
mapX - posX 가 음수이더라도 역시 음수인 rayDirX로 나누어 계산된 값은 항상 양수가 됩니다.
•
perpWallDist는 벽의 적중지점과 플레이어의 카메라 평면을 사용해서, 점에서 선까지의 거리를 구하는 공식을 적용해서 계산을 할 수도 있습니다. 하지만 이 공식은 앞의 더 간단한 공식보다는 계산량이 많습니다. 위의 이미지는 더 간단한 공식이 어떻게 도출되는지 보여줍니다.
•
이 설명은 y면에서 부딪힌 경우 (side == 1)을 보여줍니다. x 면에 부딪힌 경우도 같은 원리로 설명할 수 있습니다.
// Calculate height of line to draw on screen
int lineHeight = (int)(h / perpWallDist);
// Calculate lowest and highest pixel to fill in current stripe
int drawStart = -lineHeight / 2 + h / 2;
if(drawStart < 0)drawStart = 0;
int drawEnd = lineHeight / 2 + h / 2;
if(drawEnd >= h)drawEnd = h - 1;
JavaScript
복사
이제 계산한 거리 (perpWallDist)로, 화면에 그려야 하는 선의 높이를 구할 수 있습니다.
•
perpWallDist를 역수로 취하고, 픽셀 단위로 맞춰주기 위해 픽셀 단위의 화면 높이 h를 곱해서 구할 수 있습니다.
•
벽을 더 높게 그리거나 더 낮게 그리고 싶으면 2 * h 와 같은 다른 값을 넣을 수도 있습니다.
•
h 값은 일정한 벽의 높이, 너비 및 깊이를 가진 박스처럼 보이게 해주고, 값이 클 수록 높이가 높은 박스를 만들어줍니다.
•
이렇게 구한 lineHeight에서, 실제로 선을 그릴 위치의 시작 및 끝 위치를 알 수 있습니다.
•
벽의 중심은 화면의 중심에 있어야 하고, 이 중심점이 화면 범위 아래에 놓여있다면 0으로, 화면 범위 위에 놓여 있다면 h - 1 으로 덮어씌웁니다.
// Choose wall color
ColorRGB color;
switch(worldMap[mapX][mapY])
{
case 1: color = RGB_Red; break; //red
case 2: color = RGB_Green; break; //green
case 3: color = RGB_Blue; break; //blue
case 4: color = RGB_White; break; //white
default: color = RGB_Yellow; break; //yellow
}
// Give x and y sides different brightness
if (side == 1) {color = color / 2;}
// Draw the pixels of the stripe as a vertical line
verLine(x, drawStart, drawEnd, color);
C++
복사
•
마지막으로, 광선이 부딪힌 벽의 색상값에 따라 표현할 색상을 선택해줍니다.
◦
y 면에 부딪힌 경우에 색상을 더 업두게 설정하면 더 그럴듯하게 표현해 줄 수 있습니다.
◦
그리고 verLine()함수로 수직선을 그려줍니다.
◦
여기가지의 과정을 모든 x 값에 대해 반복한 후 이것으로 raycasting loop가 종료됩니다.
//timing for input and FPS counter
oldTime = time;
time = getTicks();
double frameTime = (time - oldTime) / 1000.0; //frameTime is the time this frame has taken, in seconds
print(1.0 / frameTime); //FPS counter
redraw();
cls();
//speed modifiers
double moveSpeed = frameTime * 5.0; //the constant value is in squares/second
double rotSpeed = frameTime * 3.0; //the constant value is in radians/second
C++
복사
레이캐스팅 loop를 마친 후, 현재 프레임과 이전 프레임의 시간을 계산합니다.
•
FPS가 계산되고 출력됩니다.
•
벽과 FPS 카운터의 값을 포함한 모든 것이 화면에 표시될 수 있도록 다시 그려집니다.
•
루프가 완료된 후 현재 및 이전 프레임의 시간이 계산되고 FPS가 계산 및 인쇄되며 벽 및 fps 값을 모드 화면에 보이게 하도록 화면을 다시 그립니다.
•
cls()를 실행해서 backbuffer가 비워지고 다시 다음 프레임을 그릴 때 바닥과 천장이 그전의 프레임의 픽셀로 보이는 것이 아니라 검은색이 되도록 합니다.
speed modifier는 frame timerhk 상수를 이용해 입력키로 인한 이동속도 또는 회전속도를 결정합니다.
•
frameTime을 사용하면 이동속도 또는 회전속도를 프로세서의 속도와는 독립적으로 설정할 수 있습니다.
readKeys();
//move forward if no wall in front of you
if (keyDown(SDLK_UP))
{
if(worldMap[int(posX + dirX * moveSpeed)][int(posY)] == false) posX += dirX * moveSpeed;
if(worldMap[int(posX)][int(posY + dirY * moveSpeed)] == false) posY += dirY * moveSpeed;
}
//move backwards if no wall behind you
if (keyDown(SDLK_DOWN))
{
if(worldMap[int(posX - dirX * moveSpeed)][int(posY)] == false) posX -= dirX * moveSpeed;
if(worldMap[int(posX)][int(posY - dirY * moveSpeed)] == false) posY -= dirY * moveSpeed;
}
//rotate to the right
if (keyDown(SDLK_RIGHT))
{
//both camera direction and camera plane must be rotated
double oldDirX = dirX;
dirX = dirX * cos(-rotSpeed) - dirY * sin(-rotSpeed);
dirY = oldDirX * sin(-rotSpeed) + dirY * cos(-rotSpeed);
double oldPlaneX = planeX;
planeX = planeX * cos(-rotSpeed) - planeY * sin(-rotSpeed);
planeY = oldPlaneX * sin(-rotSpeed) + planeY * cos(-rotSpeed);
}
//rotate to the left
if (keyDown(SDLK_LEFT))
{
//both camera direction and camera plane must be rotated
double oldDirX = dirX;
dirX = dirX * cos(rotSpeed) - dirY * sin(rotSpeed);
dirY = oldDirX * sin(rotSpeed) + dirY * cos(rotSpeed);
double oldPlaneX = planeX;
planeX = planeX * cos(rotSpeed) - planeY * sin(rotSpeed);
planeY = oldPlaneX * sin(rotSpeed) + planeY * cos(rotSpeed);
}
}
}
C++
복사
예제코드의 마지막 부분은 입력키를 다룹니다. 우선 readKeys()로 입력된 키값을 읽어옵니다.
•
위쪽 화살표가 눌렸다면 플레이어는 앞으로 이동해야 하므로 posX에는 dirX를, posY에는 dirY를 더해줍니다.
•
이것은 dirX와 dirY가 정규화된 벡터(길이 1)인 것을 전제로 합니다.
•
위 코드에는 간단한 충돌감지 기능도 포함되어있습니다. 새로운 위치가 벽에 포함된다면 플레이어가 움직이지 않도록 합니다.
•
이 충돌감지 기능은 플레이어 위치 단일지점 대신에 플레이어를 중심으로 하는 원을 그려, 이 원이 벽 내부로 들어가는지 확인하는 방식으로 개선할 수도 있습니다.
•
왼쪽 화살표 또는 오른쪽 화살표가 눌려서 회전시켜야 한다면, 회전행렬을 곱하는 공식을 이용해서 방향벡터와 카메라평면벡터 둘 다 회전시켜줍니다.
Textured raycaster
textured 와 untextured 의 핵심은 같습니다. 다만, textured 에서는 각 pixel 이 texture 의 어떤 pixel 을 가지는지를 계산해주는 작업을 해야 합니다.
verLine() 함수로 수직선을 그리는 방식을 사용하지 않습니다. 대신 픽셀을 하나하나 그려주는 방식을 통해 텍스쳐를 적용할 것입니다. 가장 좋은 방법은 스크린버퍼로 2차원 배열을 사용해서 화면에 한 번 출력해주는 것입니다. 이 방법이 pset(점을 찍는 함수) 을 사용하는 것보다 훨씬 빠릅니다.
텍스쳐를 위한 별도의 배열이 필요합니다. drawbuffer 함수는 int 하나의 값으로 작동합니다.
int main(int argc, char *argv[])
{
double posX = 22.0, posY = 11.5; //x and y start position
double dirX = -1.0, dirY = 0.0; //initial direction vector
double planeX = 0.0, planeY = 0.66; //the 2d raycaster version of camera plane
double time = 0; //time of current frame
double oldTime = 0; //time of previous frame
Uint32 buffer[screenHeight][screenWidth]; // y-coordinate first because it works per scanline
std::vector texture[8];
for(int i = 0; i < 8; i++) texture[i].resize(texWidth * texHeight);
C++
복사
스크린 버퍼 배열 buffer 와 텍스처 배열 벡터를 선언합니다. std::vector로 텍스처 배열은 총 8가지 종류의 텍스처를 저장할 수 있고, 위에서 define한 texWidth, texHeight 만큼의 크기를 갖게 합니다.
screen(screenWidth,screenHeight, 0, "Raycaster");
//generate some textures
for(int x = 0; x < texWidth; x++)
{
for(int y = 0; y < texHeight; y++)
{
int xorcolor = (x * 256 / texWidth) ^ (y * 256 / texHeight);
//int xcolor = x * 256 / texWidth;
int ycolor = y * 256 / texHeight;
int xycolor = y * 128 / texHeight + x * 128 / texWidth;
texture[0][texWidth * y + x] = 65536 * 254 * (x != y && x != texWidth - y); //flat red texture with black cross
texture[1][texWidth * y + x] = xycolor + 256 * xycolor + 65536 * xycolor; //sloped greyscale
texture[2][texWidth * y + x] = 256 * xycolor + 65536 * xycolor; //sloped yellow gradient
texture[3][texWidth * y + x] = xorcolor + 256 * xorcolor + 65536 * xorcolor; //xor greyscale
texture[4][texWidth * y + x] = 256 * xorcolor; //xor green
texture[5][texWidth * y + x] = 65536 * 192 * (x % 16 && y % 16); //red bricks
texture[6][texWidth * y + x] = 65536 * ycolor; //red gradient
texture[7][texWidth * y + x] = 128 + 256 * 128 + 65536 * 128; //flat grey texture
}
}
C++
복사
이제 메인함수를 시작합니다. 제일 먼저 텍스쳐 생성부터 해줍니다. 텍스처 크기의 모든 픽셀은 텍스처 높이와 너비만큼 이중 반복문을 통과하면서, 텍스처 번호마다 x, y, 값으로 만든 특정한 값을 갖게 됩니다.
//texturing calculations
int texNum = worldMap[mapX][mapY] - 1; //1 subtracted from it so that texture 0 can be used!
//calculate value of wallX
double wallX; //where exactly the wall was hit
if (side == 0) wallX = posY + perpWallDist * rayDirY;
else wallX = posX + perpWallDist * rayDirX;
wallX -= floor((wallX));
//x coordinate on the texture
int texX = int(wallX * double(texWidth));
if(side == 0 && rayDirX > 0) texX = texWidth - texX - 1;
if(side == 1 && rayDirY < 0) texX = texWidth - texX - 1;
C++
복사
•
이전 코드에서 벽의 색상을 선택해 주었다면, 이번 코드에서는 벽의 텍스처를 선택해줄 것입니다. 선택된 텍스처종류를 나타내는 변수 textNum은 맵에서 광선이 부딪힌 벽 한 칸이 가진 값에서 1을 빼서 구할 수 있습니다.
•
wallX의 값은 벽의 int 형 좌표가 아닌 double 형 좌표로 벽의 정확히 어디에 부딪혔는지를 나타냅니다.
•
코드의 마지막 부분에서 wallX 로, 텍스처의 x 좌표를 나타내는 texX 를 계산해 주었습니다. 이제 우리는 벽의 텍스쳐표현을 해주기 위해 텍스처의 어떤 x 좌표 texX 를 적용해야 하는지를 알아냈습니다. 이 x 좌표는 해당 수직선 상에서 그대로 유지됩니다.
// How much to increase the texture coordinate per screen pixel
double step = 1.0 * texHeight / lineHeight;
// Starting texture coordinate
double texPos = (drawStart - h / 2 + lineHeight / 2) * step;
for(int y = drawStart; y<drawEnd; y++)
{
// Cast the texture coordinate to integer, and mask with (texHeight - 1) in case of overflow
int texY = (int)texPos & (texHeight - 1);
texPos += step;
Uint32 color = texture[texNum][texHeight * texY + texX];
//make color darker for y-sides: R, G and B byte each divided through two with a "shift" and an "and"
if(side == 1) color = (color >> 1) & 8355711;
buffer[y][x] = color;
}
}
C++
복사
이제 수직선 상 각 픽셀이 어떤 y 좌표 texY 를 갖게 할 건지를 결정하기 위해 y 방향 반복문을 둘 차례입니다. 반복문을 돌면서 최종적으로 구한 값을 화면버퍼 buffer[y][x] 에 하나하나 넣어줄 것입니다.
•
texY 의 값은 첫 줄에서 계산한 step 의 크기만큼 증가하면서 계산됩니다.step 의 크기는 텍스처의 좌표를 수직선 상에 있는 좌표에 대해 얼마나 늘려야 하는지에 따라 결정됩니다. 그리고 부동소수점 수인 double형에서 int형으로 캐스팅해주어 텍스처 픽셀값을 선택할 수 있도록 합니다.화면버퍼 buffer[y][x]에 넣을 픽셀의 색상 color 는 texture[texNum][texX][texY] 로 쉽게 가져올 수 있습니다.
•
색상만 있는 레이캐스터 때와 마찬가지로 광선이 벽의 y면에 부딪힌 경우(side == 1)에 색상값은 좀 더 어둡게 표현해 줄 겁니다. (그렇게 해야 좀 더 자연스러운 조명표현이 되기 때문입니다.)
◦
그런데 색상값이 R, G, B 3개로 나뉘어져 있는게 아니라 하나의 int 값으로 되어있어서, 계산방식이 직관적이지는 않습니다.
◦
R, G, B를 2로 나누어서 색상을 어둡게 해주려고 합니다.
◦
십진수를 10으로 나누면 마지막 자리를 없앨 수 있는 것처럼 (300 / 10 하면 30으로 마지막 숫자 0이 제거됨) 이진수를 2로 나누는 것은 마지막 비트를 제거하는 것과 같습니다.
◦
여기서는 비트연산 중 오른쪽 시프트연산 >>1 을 사용해서 마지막 비트를 제거해주었습니다.
◦
그런데 여기서는 24비트 int형(실제로 32 비트이지만 첫 8비트는 사용되지 않음)을 시프트연산 해주는 것이라 이전 8비트의 마지막 비트가 다음 8비트의 첫 번째 비트가 되어 색상 값 전체가 엉망이 될 수 있습니다!
◦
따라서 시프트연산 후, 모든 바이트의 첫 번째 비트는 0으로 설정해주어야 하고, 방법은 이진수 01111111 01111111 01111111(10진수로는 8355711)를 AND연산해주면 됩니다.
◦
따라서 위 예제코드처럼 해주면 실제보다 어두운 색으로 설정해줄 수 있습니다.
◦
최종적으로 계산된 color 의 값이 현재 버퍼픽셀의 색상으로 설정되면 반복문의 한 사이클을 마치고 다음 y로 넘어갑니다.