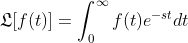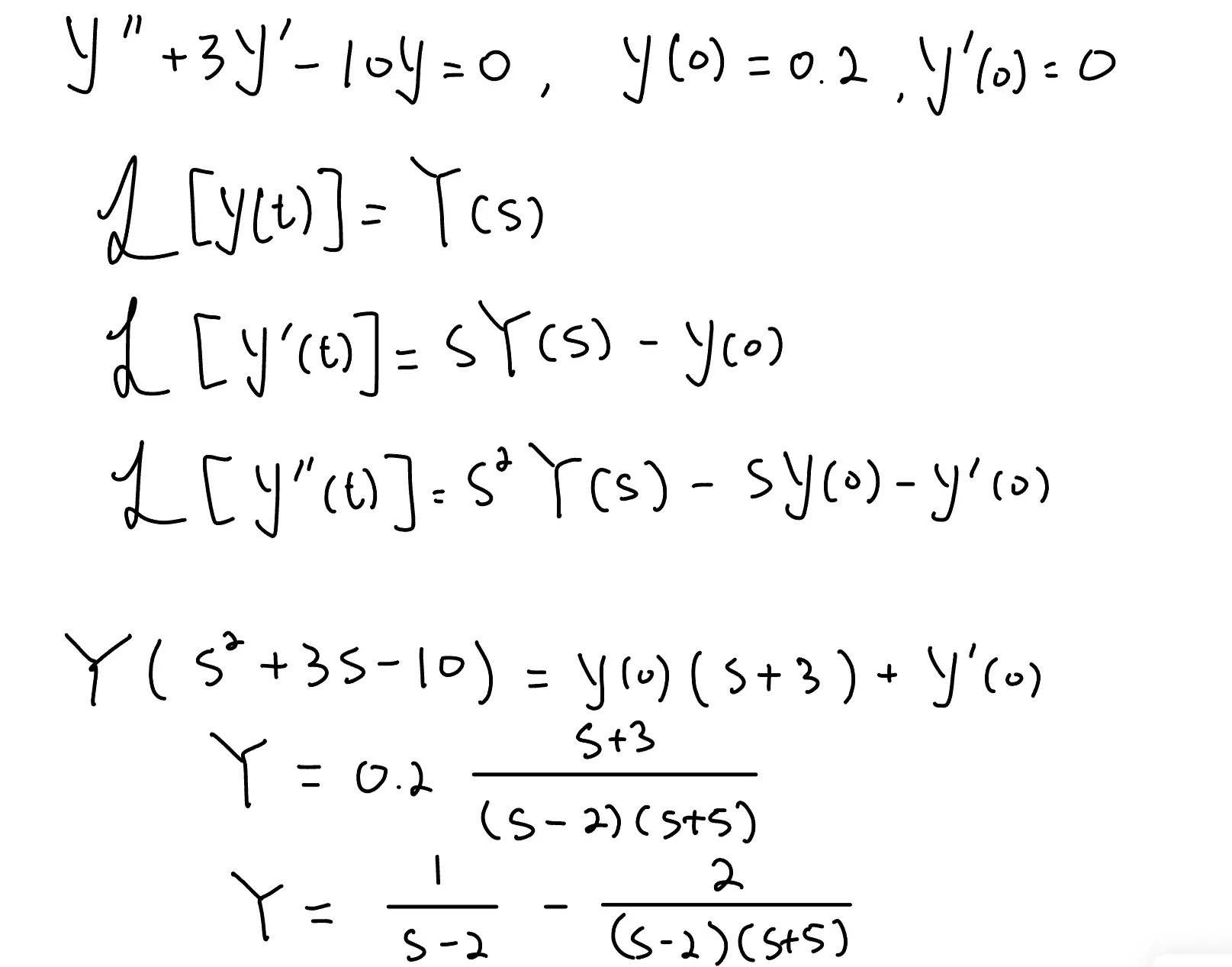Subject
라플라스 변환이란?
sympy를 이용한 라플라스변환
1. 라플라스 변환이란?
1) 개요
복잡한 선형 미분방정식을 풀기 위한 방법으로, 미분방정식(시간 등)에 대한 영역에서 다른 공간의 식으로 변환하여 간단한 대수방정식 혹은 미분방정식을 얻어내고, 이의 해를 구해 적절하게 라플라스 역변환을 통해 원래 공간에서의 미분방정식의 해를 구하는 방법이다.
요약하면
1.
시간 영역의 복잡한 미분방정식이 존재함
2.
이를 라플라스 변환을 통해 s에 관한 식으로 변환
3.
s-공간에서의 식의 해를 구한다
4.
그 해를 다시 t에 관한 식으로 변환하여 미분방정식의 해를 얻는다!
2) 수식
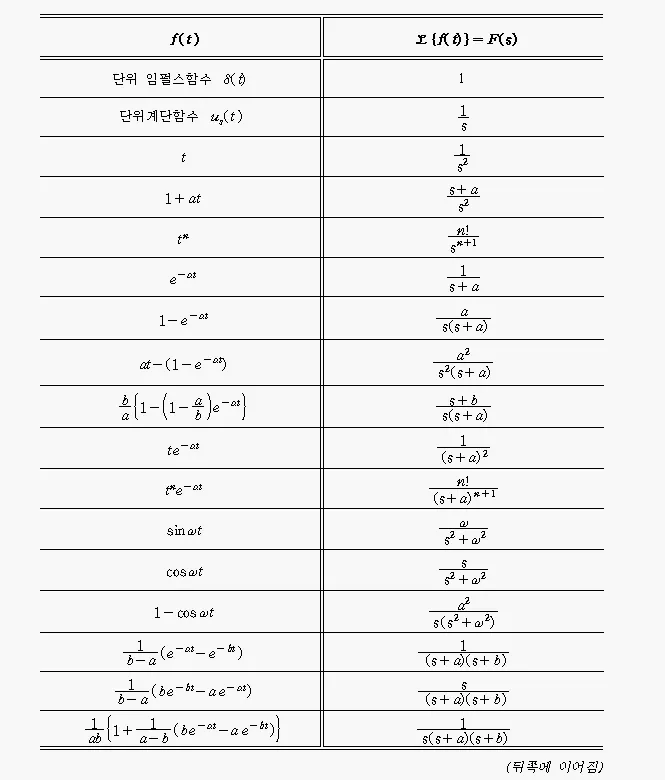
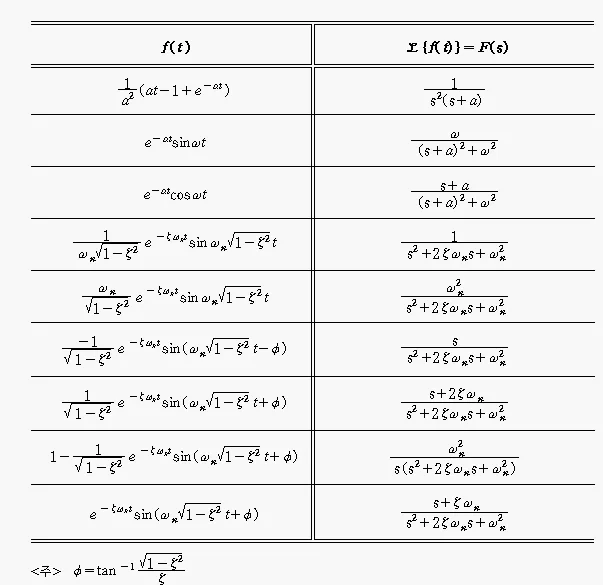
3) 라플라스 변환 표
사진 출처 : CEMTool / cemtool.com
2. SymPy를 이용한 라플라스 변환
1) SymPy 이용법
from sympy import *
#출력을 LaTex 수식으로 나타내고, matplotlib를 불러온다
x, y, z, t = symbols('x y z t')
f, g, h = symbols('f, g, h', cls=Function)
Python
복사
#laplace 변환과, 역변환 모듈을 불러온다
from sympy.integrals.transforms import laplace_transform
from sympy.integrals.transforms import inverse_laplace_transform
s = symbols('s')
a, ω = symbols('a ω', constant=True, positive=True)
n = symbols('n', constant=True, integer=True)
Python
복사
#변환표에 따라 변환됨, 만약 0, True는 수렴과 관련된 사항으로 만약 변환만을 보고싶다면,
#옵션으로 noconds=True를 주게되면 변환만 출력됨
#e^(at)를 표현하고 싶다면 exp(a*t)
#heaviside 계단함수는 Heaviside(t)
#DiracDelta함수는 DiracDelta(t)
laplace_transform( 1, t, s )
Python
복사
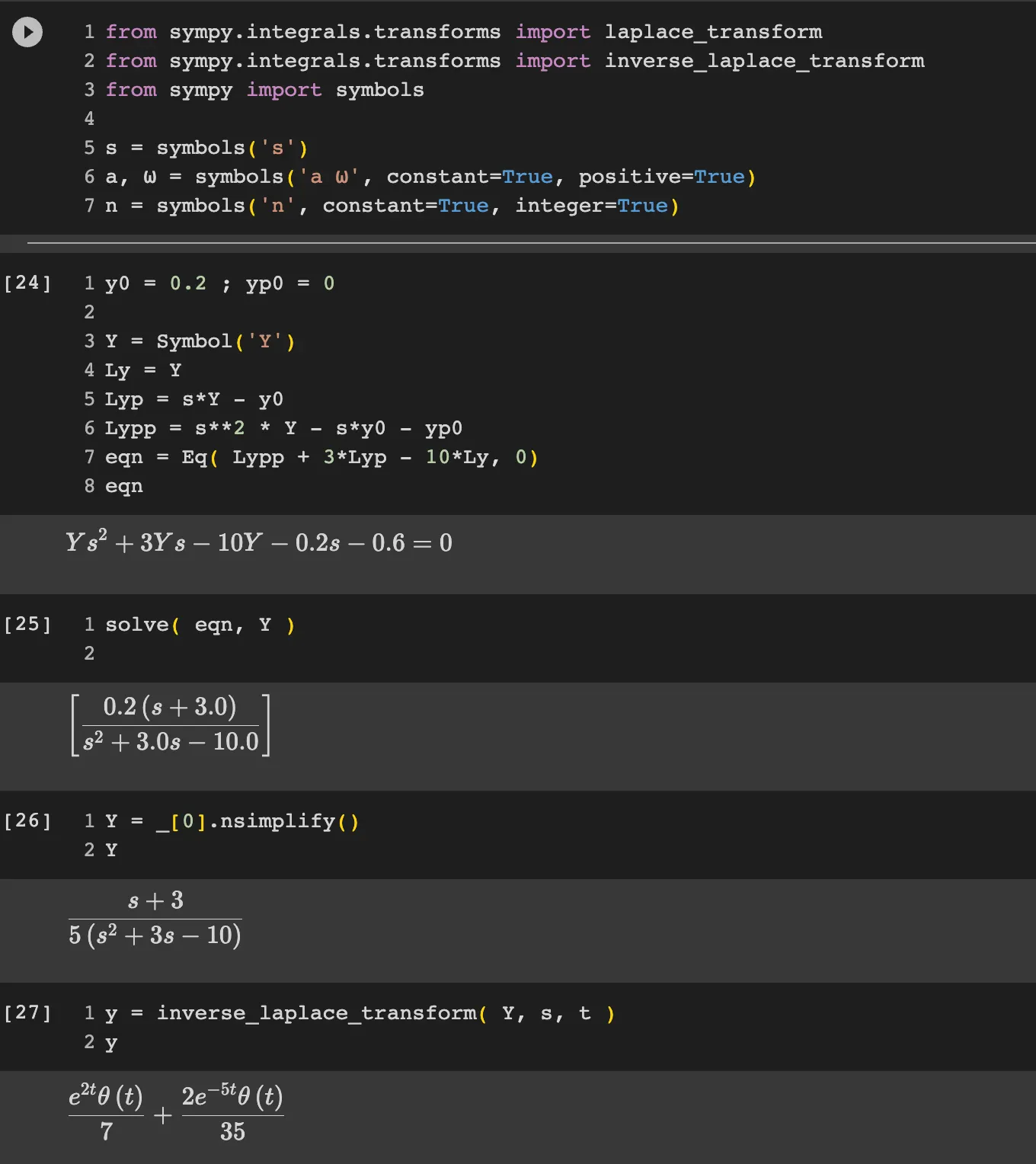
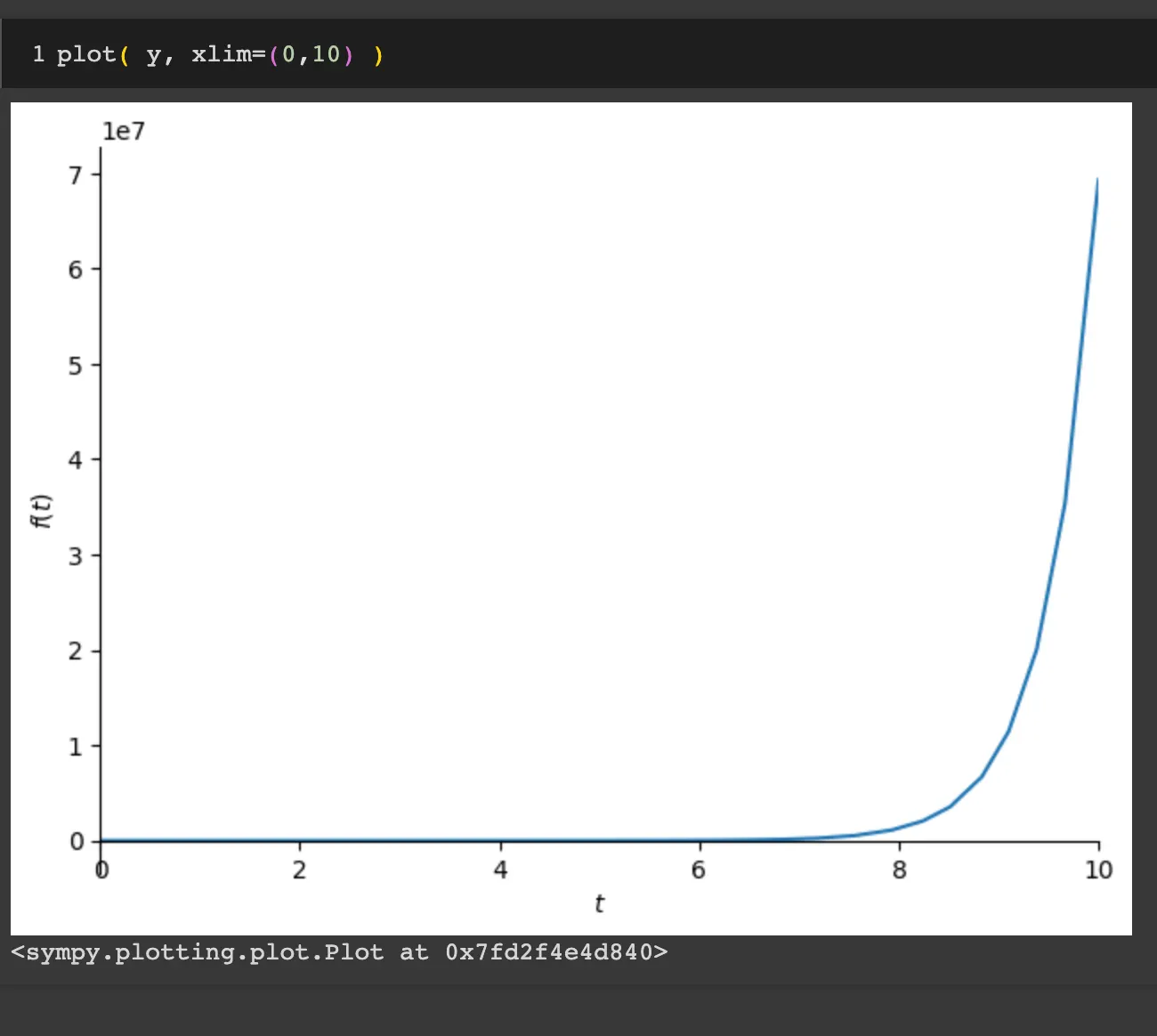
2) 예제
결론
matlab이 아니더라도 파이썬에도 충분히 많은 해석도구가 존재한다! 파이썬을 애용합시다~~