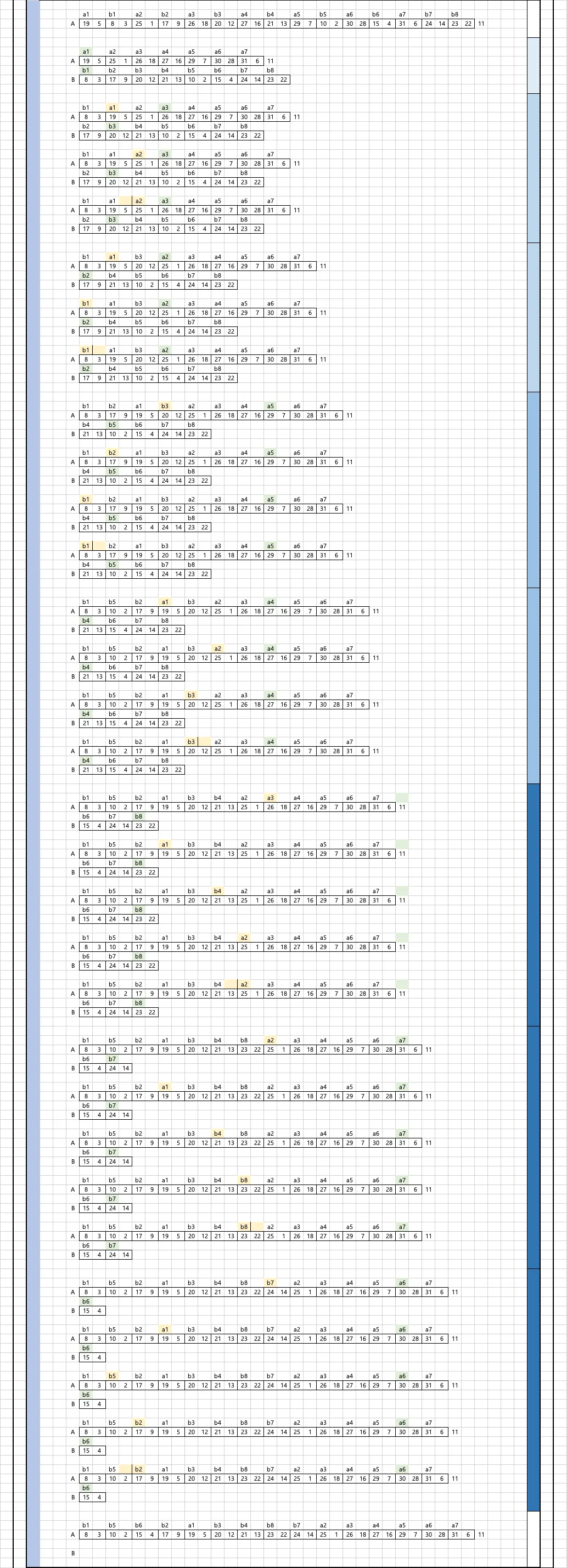
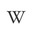cpp-module-09 ex02에서 만난 ford-johnson algorithm은 merge-insertion sort라고 불리는 정렬 방식인데 과제를 진행하기 앞서 해당 알고리즘에 대해 찾아볼 때 위키피디아 말고는 해당 알고리즘의 작동 방식에 대해서 설명하는 글을 찾아보기 힘들기도 하고 재귀적으로 정렬한다는 부분이 무엇을 의미하는지 이해하는것도 상당히 난해했던 것 같아서 평가받을때와 과제를 진행중인 다른 동료분들께 설명드릴 때 직접 수행해보고 여러가지 중요한 지점에서 표기를 해놓은 자료를 사용하면서 설명했을 때가 가장 수월했던 것을 생각하며 한번 정리해서 올려보려 합니다.
제가 이해한 바가 맞는지는 사실 아직도 자신이 없지만 제가 이해한 바를 설명드려보겠습니다.
먼저 앞에서부터 두 원소를 한 쌍으로 여기고 큰 값을 a, 작은 값을 b로 간주해야하고 a가 정렬되어있을 때 까지 재귀적으로 반복하면서 정렬한다는 부분에 대해 기존의 a1, a2가 a1, b1으로 쌍으로서 선택되고 그 때 더 큰 값이 a 더 작은 값이 b가 되어야 한다고 봤습니다.
처음엔 pair로 접근하려 했다가 배열로서 앞에서부터 해당 loop의 node_size만큼 a1, b1, a2, b2, a3, b3 …순서대로 인식하되 쌍이 될 수 없지만 node 하나는 만들어지는 경우 a(n), b(n), b(n+1)으로 인식하고 그렇지 않은 경우는 a(n), b(n)으로 인식한다고 가정하면서 진행했습니다.
더 큰 값을 선택하는 것을 구현하기 위해 더 큰 값을 가진 node가 b라면 해당 node의 쌍의 값이 바뀌도록 swap해주었습니다.
a가 하나밖에 없다면 ascending이니 최소 한 쌍이 존재하고 a가 하나일 때 까지 묶도록 하였고 a가 하나인 경우는 곧 다음 loop에서는 더이상 쌍을 만들 수 없어 다음 루프에서 쌍을 만들 수 있을때만 재귀적으로 호출하는 경우도 같은 동작을 하는 구조입니다.
재귀적으로 a가 정렬되어있을때까지 반복하여 깊이를 늘렸고 깊어질 때 마다 node의 size는 두배씩 늘어나도록 만들었습니다.
한 쌍만 존재할 때 가능한 경우의 수는 [a1, b1] [a1, b1, b2]이고 이번 경우는 후자였습니다.
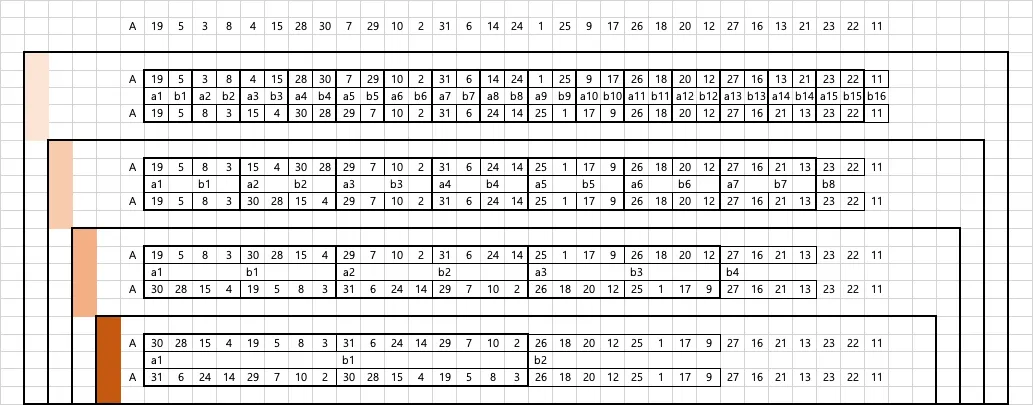
정렬을 시작하기 앞서 b를 삽입하기 위해 a와 b를 분리해주는데 node_size보다 적은 개수의 남은 원소들이 컨테이너 A에 남아있도록 하였습니다
정렬을 할 땐 이진탐색의 횟수를 기준으로 반복을 하도록 하였습니다.
이진탐색의 횟수가 n이라면 그 때의 원소 개수의 최댓값은 2^n - 1입니다.
이진탐색의 횟수가 1일 땐 이미 쌍을 만들고 큰 값을 a로 삼는 규칙에 따라 b1 < a1이므로 비교 없이 b1을 a1 앞에 삽입합니다.
b1
이진탐색의 횟수가 2일 땐 2^2 - 1 = 3, 최대 3개의 수를 비교할 수 있으며 비교해야하는, 기존에 정렬된 수의 개수는 지금까지 정렬된 b의 개수 * 2입니다.
따라서 이진탐색의 횟수가 2일 때 b2를 정렬하기 앞서 2회로 탐색 가능한 최대한의 원소는 3개지만 지금까지 정렬된 원소는 1 * 2이므로 3이 될 때 까지 다음 순서의 원소가 먼저 정렬되도록 합니다.
b3 b2
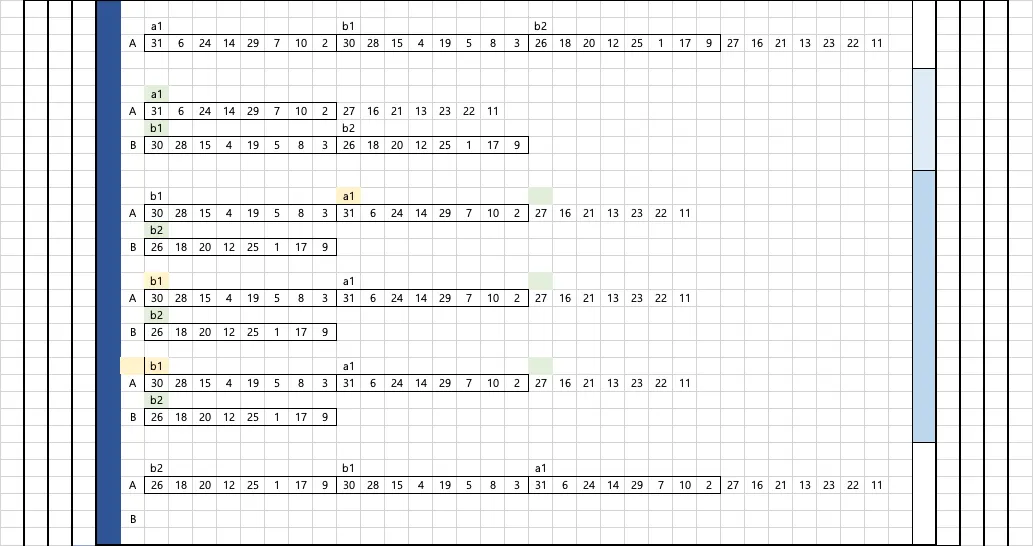
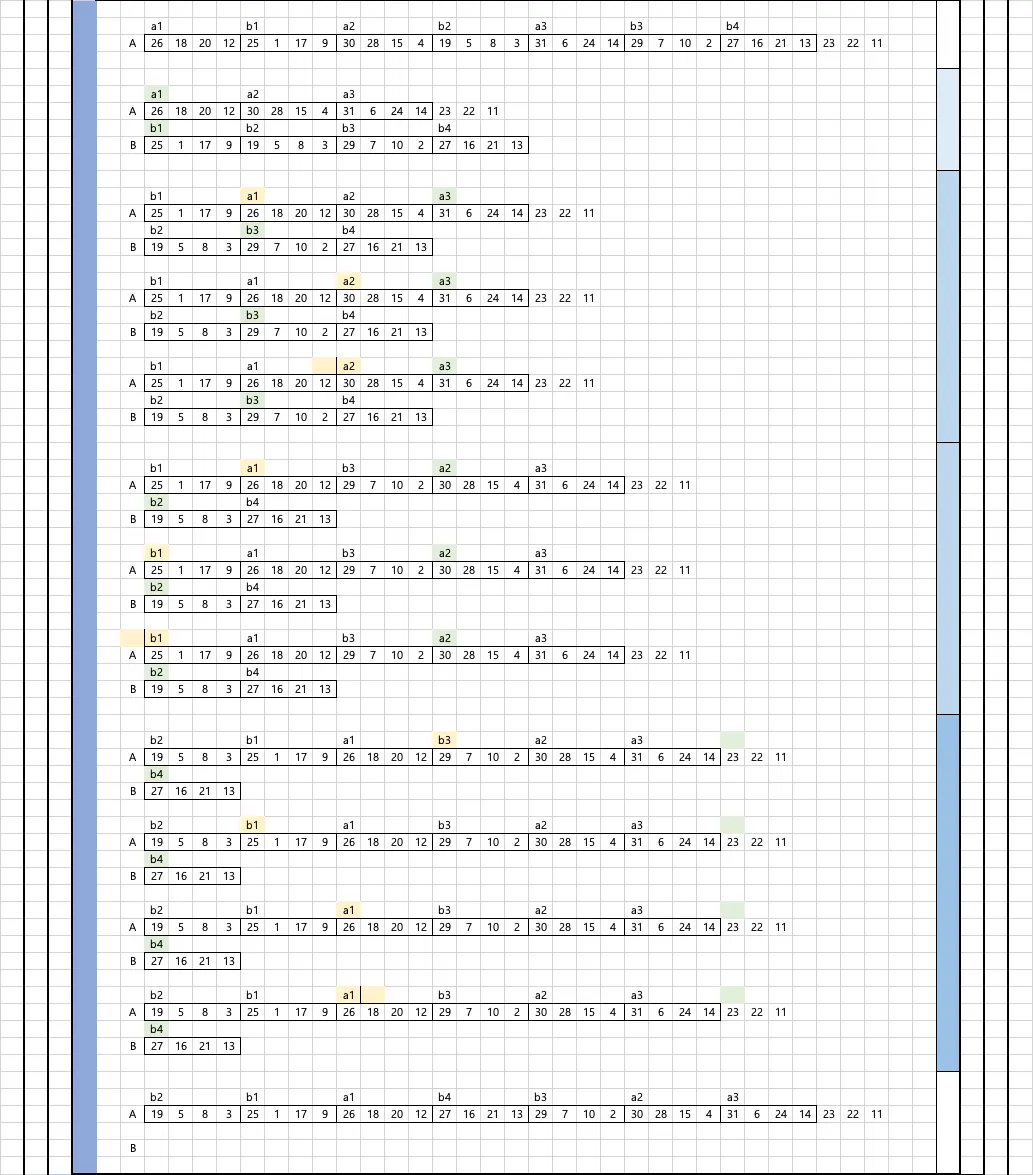
이진탐색의 횟수가 3일땐 이미 정렬된 개수는 6, 최대 7개의 수를 비교할 수 있기 때문에 한번의 양보가 발생합니다
b5 b4
이진탐색의 횟수가 4일 땐 이미 정렬된 개수는 10, 최대 15개의 수를 비교할 수 있기 때문에 6번의 양보가 발생합니다
b11 b10 b9 b8 b7 b6
이진탐색의 횟수가 5일땐 이미 정렬된 개수는 22, 최대 31개의 수를 비교할 수 있기때문에 10번의 양보가 발생합니다.
b21 b20 b19 b18 b17 b16 b15 b14 13 b13 b12
이진탐색의 횟수가 6일땐 이미 정렬된 개수는 42, 최대 63개의 수를 비교할 수 있기때문에 22번의 양보가 발생합니다.
b43 b42 b41 …
최종적으로 양보받은 수인 1 3 5 11 21 43 …은 아콥스탈 수열을 다르고 있습니다.
과제를 진행할 땐 야콥스탈 수열을 구해 순서를 찾던지 아니면 이진탐색의 횟수를 최대한 낮게 유지하는 원리대로 양보하던지 취항에 따라 선택적으로 적용하면 된다고 생각합니다.
깊이 = 4, node_size = 8 일 때
깊이 = 3, node_size = 4 일 때
(깊이 4일때의 정렬로 a는 정렬되어있다는 것을 확인할 수 있습니다.)
깊이 = 2, node_size = 2 일 때
깊이 = 1, node_size = 1 일 때
조금 더 고화질인 pdf입니다. 이미지와 내용물은 같습니다.