Memo
고려사항
•
Memorization
•
적은 메모리 사용
이번 문제 로직은 어렵지 않았으나 가장 최적의 벡터 메모리 할당을 고민하기 위해 많은 생각을 하였다.
2차원 벡터를 필요한 만큼만 초기화하고 싶어서 많은 고생을 했다.
일단 필요한 공간은 아래와 같다.
dp[0] -> 1 : 1
dp[1] -> 2 : 2 1
dp[2] -> 3 : 3 3 1
dp[3] -> 4 : 4 6 4 1
dp[4] -> 5 : 5 10 10 5 1
dp[5] -> 6 : 6 15 20 15 6 1
정확이 대칭을 만들기 위해 첫 칸을 1로 채워준 후
dp[0] -> 1 : 1 1
dp[1] -> 2 : 1 2 1
dp[2] -> 3 : 1 3 3 1
dp[3] -> 4 : 1 4 6 4 1
dp[4] -> 5 : 1 5 10 10 5 1
dp[5] -> 6 : 1 6 15 20 15 6 1
중복되는 값을 없애기 위해 절반으로 나누면
dp[0] -> 1 : 1
dp[1] -> 2 : 1 2 -
dp[2] -> 3 : 1 3 - -
dp[3] -> 4 : 1 4 6 - -
dp[4] -> 5 : 1 5 10 - - -
dp[5] -> 6 : 1 6 15 20 - - -
우선 m 개의 라인이 필요한데 각 라인마다 m개의 공간을 할당할 필요가 없었다.
라인 인덱스가 홀수인 경우에는(실제로는 m이 짝수일때) 의 값과 의 값이 동일하고 그 가운데를 기준으로 좌우 대칭이다.
라인 인덱스가 짝수인 경우에는(실제로는 m이 홀수일떄) 가운데 값을 기준으로 좌우 대칭이다.
위 풀이를 토대로 동적할당해야하는 사이즈를 식으로 정리해보면
•
size =
dp.resize(m);
for(int i = 0 ; i < m ; i++)
dp[i] = std::vector<int>(((i + 1) >> 1) + 1, 1);
C++
복사
점화식은 아래와 같다.
•
dp[i][j] = dp[i - 1][j] + dp[i - 1][j - 1]
하지만 이제 인덱스가 홀수번째인 라인은 dp[i - 1][j]값이 없다. 하지만 거기에 있어야 할 값은 dp[i - 1][j - 1]과 동일한 값이기 때문에 그냥 x 2 만 해주면 된다.
삼항연산을 활용해서 어렵지 않게 해결하였다.
dp[i][j] = (i % 2) && (j == (i >> 1) + 1) \
? dp[i - 1][j - 1] << 1 \
: dp[i - 1][j] + dp[i - 1][j - 1];
C++
복사
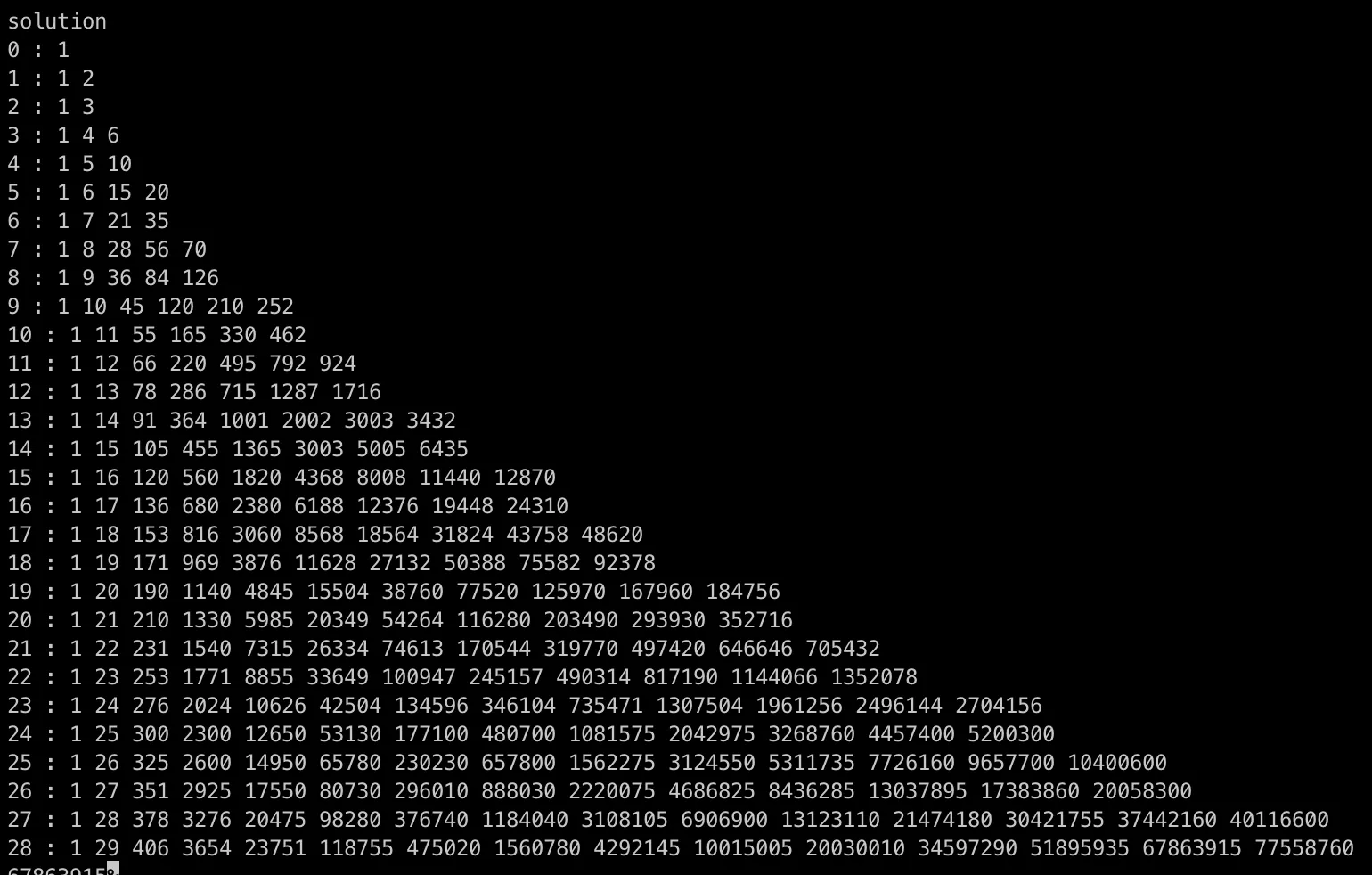
아래 사진은 실제로 동적할당 하였을 때 생성되는 테이블의 사이즈이다.
1차원 벡터로 선언할수도 있지만 가독성이 너무 떨어지고 인덱스 접근에서 실수를 할 가능성이 높기 때문에 2차원벡터를 활용하였다.
Code
제출 날짜
@3/13/2021
메모리
2016 KB
시간
0 ms
불친절한 코드
// 1010 번
#include <iostream>
#include <vector>
#include <algorithm>
int T;
int N, M;
int max;
std::vector<int> ip;
std::vector<std::vector<int> > dp;
void output()
{
for (int i = 0 ; i < T ; i += 2)
std::cout << dp[ip[i + 1] - 1][(ip[i] > ((ip[i + 1] - 1) >> 1) ? ip[i + 1] - ip[i] : ip[i])] << '\n';
}
void solution()
{
for(int i = 2 ; i < max ; i++)
for(int j = 1; j < (((i + 1) >> 1) + 1) ; j++)
dp[i][j] = (i % 2) && (j == (i >> 1) + 1) ? dp[i - 1][j - 1] << 1 : dp[i - 1][j] + dp[i - 1][j - 1];
}
void input()
{
std::cin >> T;
T = T << 1;
ip.resize(T);
for (int i = 0 ; i < T ; i += 2)
std::cin >> ip[i] >> ip[i + 1];
max = *std::max_element(ip.begin(), ip.end());
dp.resize(max);
for(int i = 0 ; i < max ; i++)
dp[i] = std::vector<int>(((i + 1) >> 1) + 1, 1);
if (max > 1)
++dp[1][1];
}
void preset()
{
std::ios_base::sync_with_stdio(false);
std::cin.tie(NULL);
std::cout.tie(NULL);
}
int main(void)
{
preset();
input();
solution();
output();
}
C++
복사
친절하게 수식을 풀어쓴 코드
// 1010 번
#include <iostream>
#include <vector>
int T;
int N, M;
int max;
std::vector<int> ip;
std::vector<std::vector<int> > dp;
void output()
{
for (int i = 0 ; i < T * 2 ; i+= 2)
{
if (ip[i] > ((ip[i + 1] - 1) >> 1)) // ip[i] , ip[i + 1]
ip[i] = ip[i + 1] - ip[i];
std::cout << dp[ip[i + 1] - 1][ip[i]] << '\n';
}
}
void solution()
{
for(int i = 2 ; i < max ; i++)
{
for(int j = 1; j < (((i + 1) >> 1) + 1) ; j++)
{
if ((i % 2) && (j == (i >> 1) + 1)) // 홀수이거나 마지막이면
dp[i][j] = dp[i - 1][j - 1] * 2;
else
dp[i][j] = dp[i - 1][j] + dp[i - 1][j - 1];
}
}
}
void input()
{
std::cin >> T;
ip.resize(T * 2);
for (int i = 0 ; i < T * 2 ; i += 2)
{
std::cin >> ip[i] >> ip[i + 1];
max = std::max(max , ip[i + 1]);
}
dp.resize(max);
for(int i = 0 ; i < max ; i++)
dp[i] = std::vector<int>(((i + 1) >> 1) + 1, 1);
if (max > 1)
++dp[1][1];
}
void preset()
{
std::ios_base::sync_with_stdio(false);
std::cin.tie(NULL);
std::cout.tie(NULL);
}
int main(void)
{
preset();
input();
solution();
output();
}
C++
복사