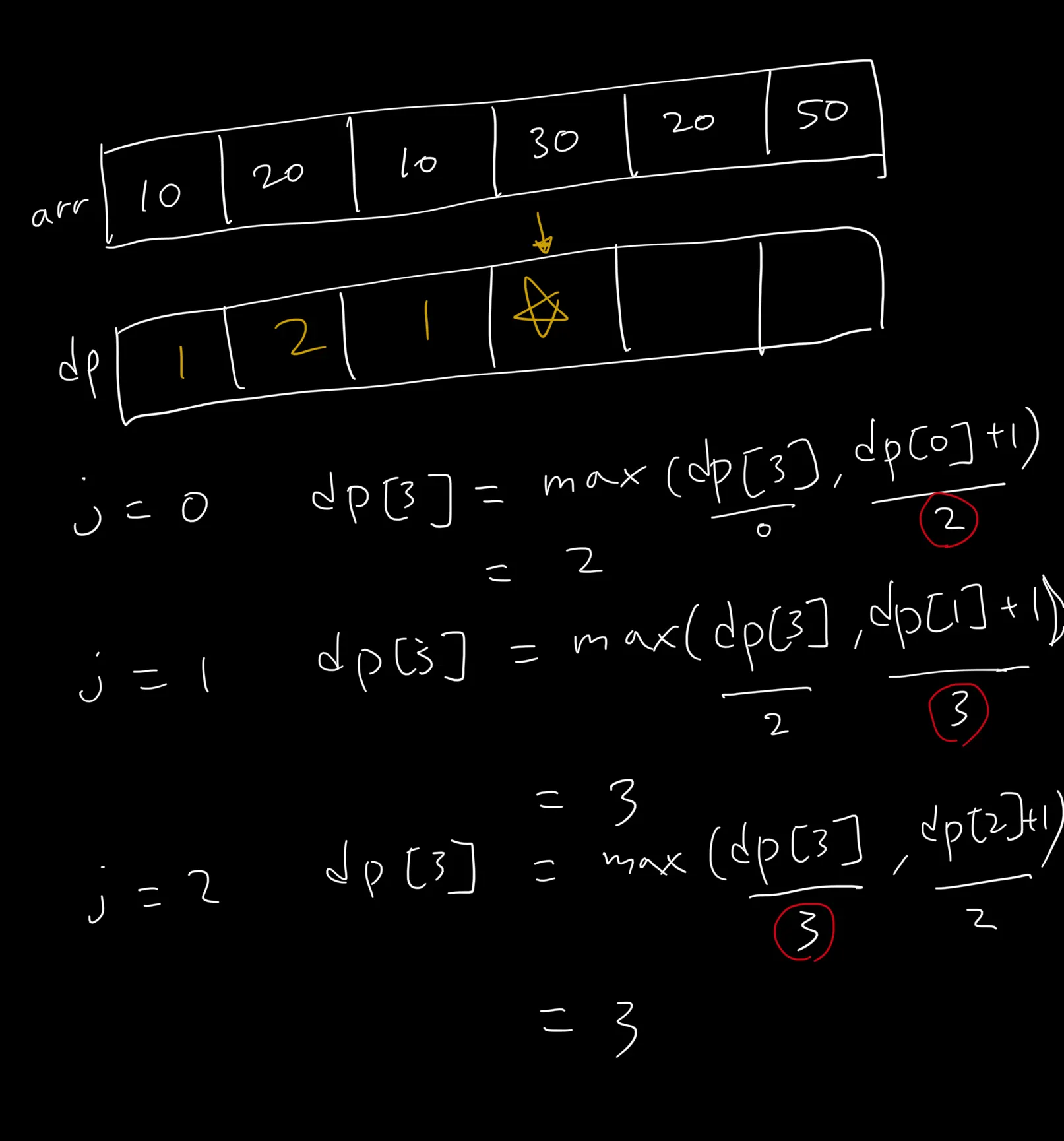Memo
1. 처음 생각 (틀렸음)
처음 이 문제를 생각할 때에는 첫번째 인덱스부터 max값을 바꿔가면서 큰 값을 찾아나가면 된다고 생각했다. 하지만 이번 문제에서는 아래와 같은 입력이 들어왔을때 출력을 고려해야 한다.
{20, 40, 1, 2, 3, 4}
즉 언제 어디서 가장 긴 증가하는 부분수열이 나올지 모르는 것이다.
따라서 DP배열을 사용해서 해당 문제를 접근하였다.
2. dp 적용하기
첫 시도는 방문한 인덱스에서 N까지 가면서 max값보다 큰 값이 나오면 result를 늘려주는 방식으로 구현하였다. 하지만 이렇게 하니 dp배열이 제대로 작동하지 않았다. 그래서 반대로 0에서 현재 방문한 인덱스까지 나보다 작은 칸의 개수를 세기로 하였다.
아래는 배열이 들어왔을 때, dp[3]을 구하는 방법이다.
루프를 통해 0 ~ N - 1(즉, 2)까지 돌면서 기존에 저장해 나가던 값과 해당 인덱스에서의 최대값을 비교해서 결과를 도출한다.
Code
제출 날짜
@2/23/2021
메모리
2016 KB
시간
0 ms
#include <iostream>
#include <vector>
int N;
int result;
std::vector<int> arr;
std::vector<int> dp;
void output()
{
std::cout << result;
}
void solution()
{
for (int i = 0 ; i < N ; i++)
{
for (int j = 0 ; j < i ; j++)
{
if (arr[i] > arr[j])
dp[i] = std::max(dp[i], dp[j] + 1);
}
result = std::max(result, dp[i]);
}
}
void input()
{
std::cin >> N;
arr.resize(N);
dp = std::vector(N, 1);
for (int i = 0 ; i < N ; i++)
std::cin >> arr[i];
}
void preset()
{
std::ios_base::sync_with_stdio(false);
std::cin.tie(NULL);
std::cout.tie(NULL);
}
int main()
{
preset();
input();
solution();
output();
}
C++
복사