Memo
이번 문제는 점화식은 눈에 쉽게 보였지만 이유를 찾기 어려운 문제였다.
P(10)까지 첫 10개의 숫자는
•
1, 1, 1, 2, 2, 3, 4, 5, 7, 9
이다. 사실 숫자를 보고 바로 규칙을 찾아버려서 어렵지는 않았지만 왜 그렇게 되는지 찾아보는데 많은 시간을 썼다.
일단 이 문제를 풀 수 있는 점화식은 두가지이다.
•
dp[N] = dp[N - 2] + dp[N - 3]
•
dp[N] = dp[N - 1] + dp[N - 5]
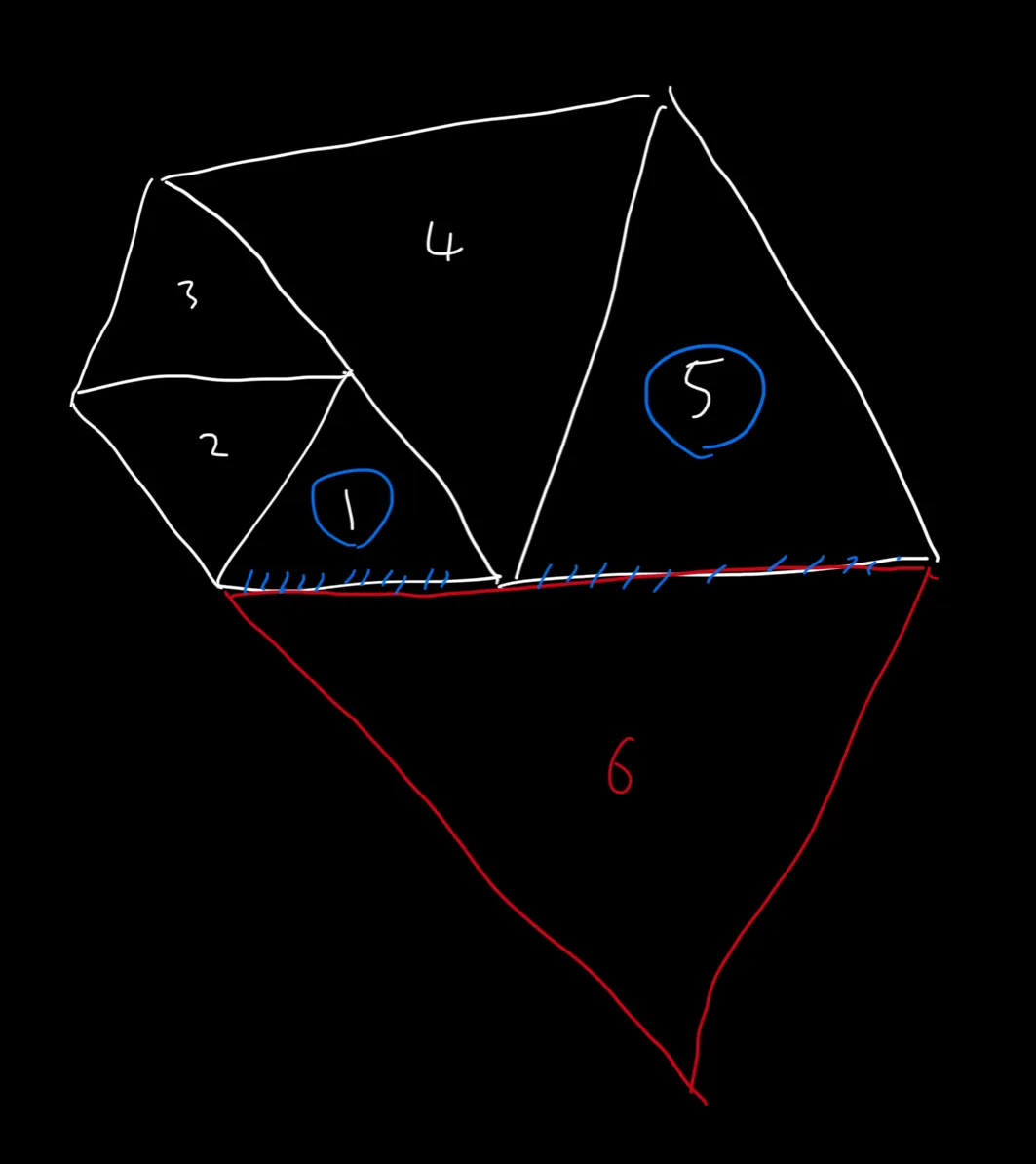
일단 그나마 쉽게 보이는 dp[N] = dp[N - 1] + dp[N - 5] 부터 확인해보자. 아래 P(6)까지 그려진 도형을 보면 6번째 삼각형이 5번째와 1번째 삼각형의 선분의 합을 빗변으로 가지는 것을 알 수 있다.
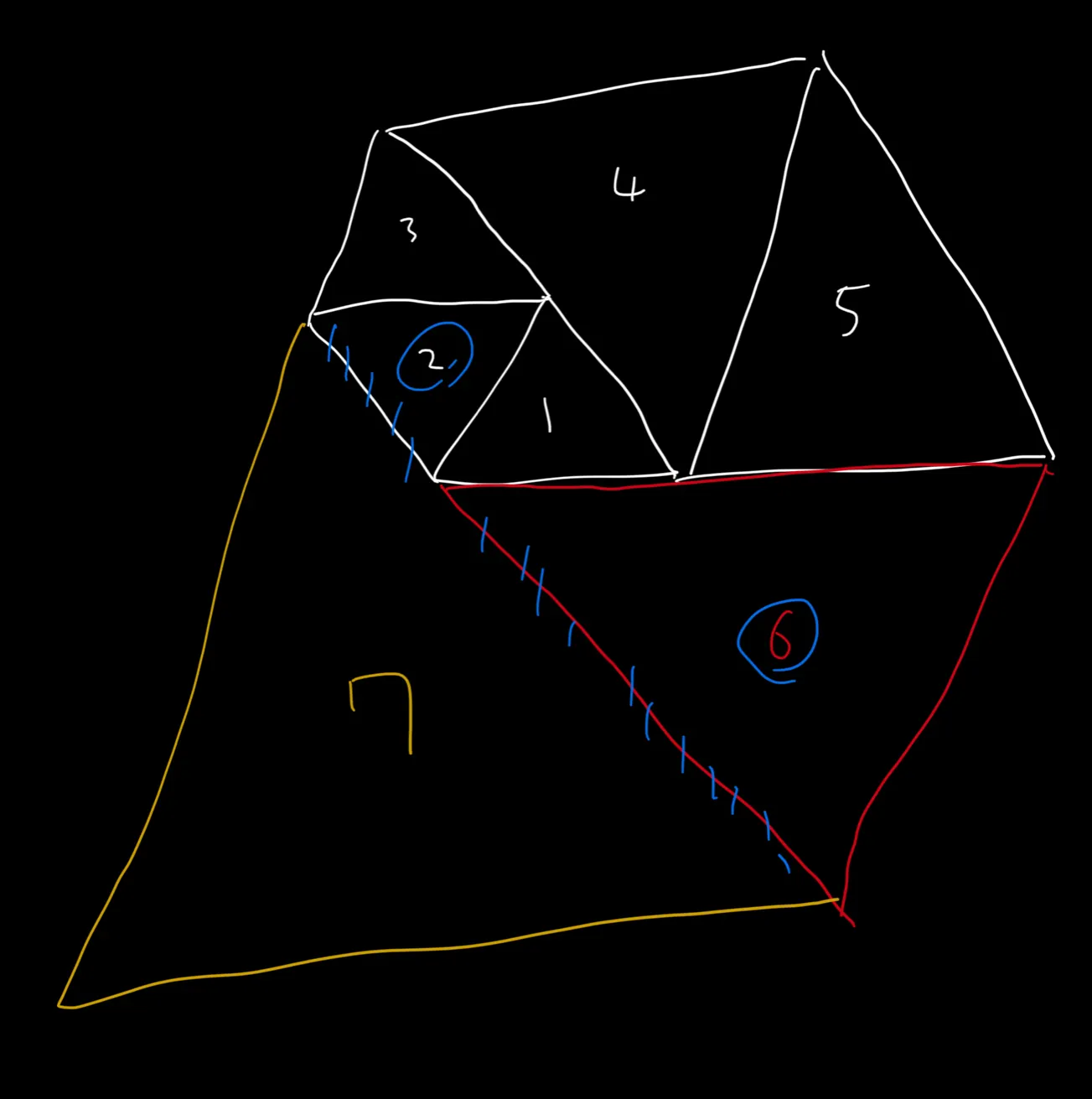
여기서 하나의 삼각형을 더 그려봐도 똑같은 규칙이 적용되는 것을 알 수 있다.
dp[N] = dp[N - 2] + dp[N - 3] 점화식은 어떤식으로 아래와 같은 형태로 증명이 가능하다.
우선 7번째 삼각형의 노란색 굵은 선의 길이를 알려고 한다.
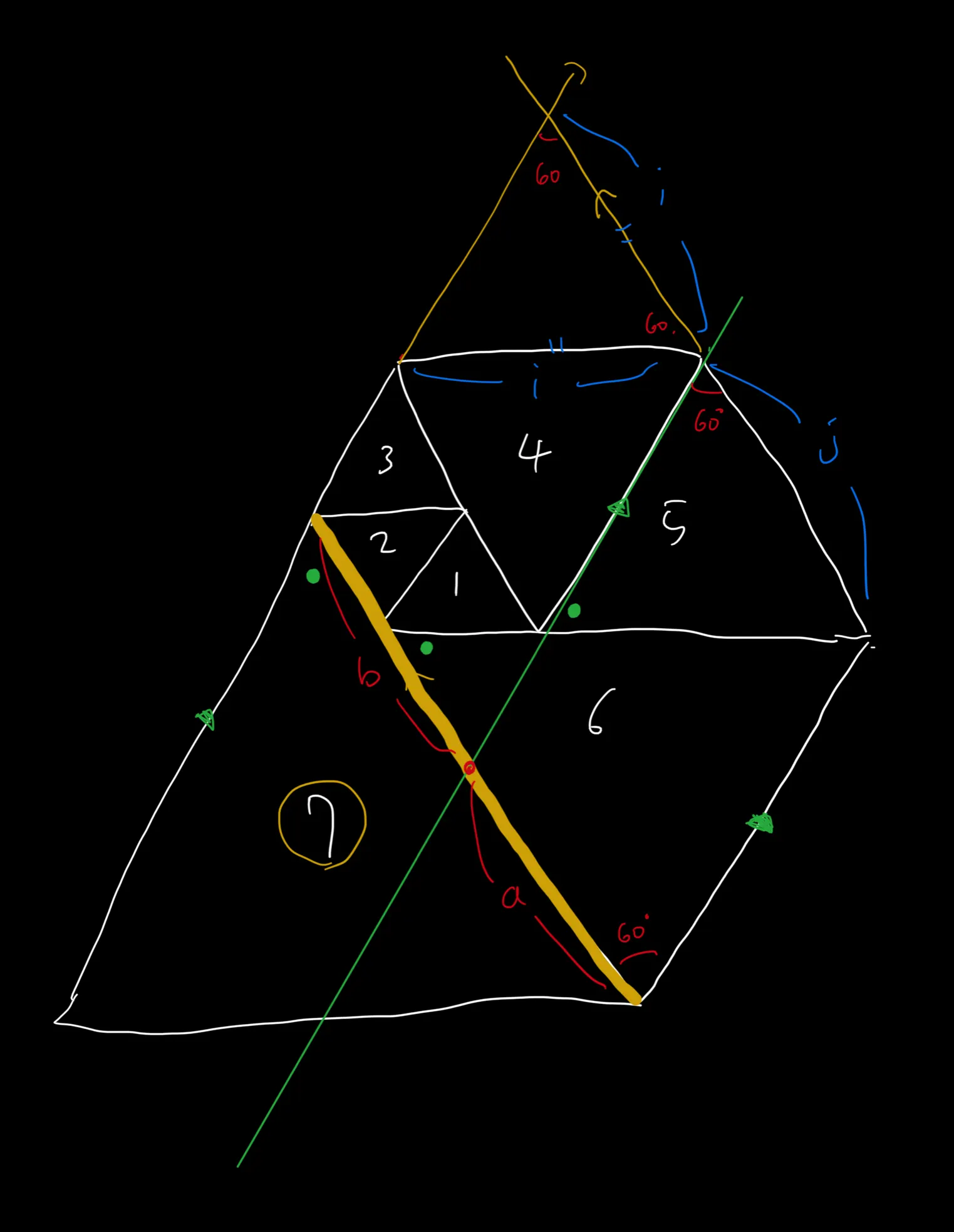
여기서 우리는 모든삼각형이 정삼각형이므로 한 내각의 크기가 60도이다.
60 * 3은 180도이다. 즉 초록색 점 3 개는 모두 60도이고, 이 때 초록색 화살표를 가지고 있는 선들은 모두 평행이 된다.
이 선을 기준으로 길이 a, b를 나누었다.
우선 a를 구해보자. 우리는 평행선을 기준으로 a변을 가지는 사각형의 6번삼각형 쪽 예각이 60도인 것을 알 수 있다. 그리고 반대푠 5번 삼각형쪽의 예각도 60도인 것을 알 수 있다. 사각형의 두 변이 평행이고 반대되는 각도의 크기가 같으므로 이 사각형은 평행사변형인 것을 알 수 있다.
평행사변형은 마주보는 변의 길이가 같으므로 우리는 a = j를 유추해 낼 수 있다.
이때 j는 N - 2번째 삼각형의 한 변의 길이이다. ( N, N - 1, N - 2 삼각형의 각을 합쳤을 때 나오는 180도 평행변을 기준으로 했기 때문)
이제 남은 b의 길이만 구하면 된다. 우리는 위에서 a를 가지는 선분과 j를 가지는 선분이 평행이란 것을 증명했기 때문에 j를 가지는 선분의 연장선(노란 얇은선)을 그어볼 수 있다. 또, 초록색 화살표를 가지는 선분은 모두 평행이란것을 증명했기 때문에 또 연장선을 그어볼 수 있다.
이때, i를 가지는 선분(4번 삼각형의 선분)과 j를 연장한 선분 사이의 각이 60도인 것을 알 수 있다. 또한 i를 가지는 선분(4번 삼각형의 선분)과 초록색 화살표(7번삼각형의 한 빗변을 가지는 선분)을 가지는 선분사이의 각도 60도인 것을 알 수 있다. 그렇다면 두 선분을 이어서 생긴 삼각형은 정삼각형으로 모든 변의 길이가 같은 것을 알 수 있다. 이때 생성된 사각형도 평행 사변형이므로 b = i임을 증명해 낼 수 있다.
그러므로 7번 정삼각형의 한 변의 길이 a + b 는 i + j, 즉. (7 - 2)번째 삼각형의 한 변의 길이 + (7 - 3)번째 삼각형의 한 변의 길이이다.
이것을 점화식으로 만들면 아래와 같다.
dp[N] = dp[N - 2] + dp[N - 3]
•
std::endl 은 '\n'과 출력시간 차이가 꽤 난다
Code
제출 날짜
@2/23/2021
메모리
2016 KB
시간
0 ms
#include <iostream>
#include <vector>
int T;
int N;
int m;
std::vector<long long> dp;
std::vector<int> tests;
void output()
{
for (int t = 0; t < T; t++)
//std::cout << "tests[i] : " << tests[t] << std::endl;
std::cout << dp[tests[t] - 1] << '\n';
}
void solution()
{
for (int i = 0; i < 3 && i < m; i++)
dp[i] = 1;
for (int i = 3; i < m; i++)
dp[i] = dp[i - 2] + dp[i - 3];
//for (int i = 0; i <= m; i++)
// std::cout << dp[i] << " ";
//std::cout << std::endl;
}
void preset()
{
std::ios_base::sync_with_stdio(false);
std::cin.tie(NULL);
std::cout.tie(NULL);
}
void input()
{
std::cin >> T;
tests.resize(T);
for (int i = 0; i < T; i++)
{
std::cin >> tests[i];
m = std::max(m, tests[i]);
}
dp.resize(m);
}
int main()
{
preset();
input();
solution();
output();
}
C++
복사