1. 문제풀이
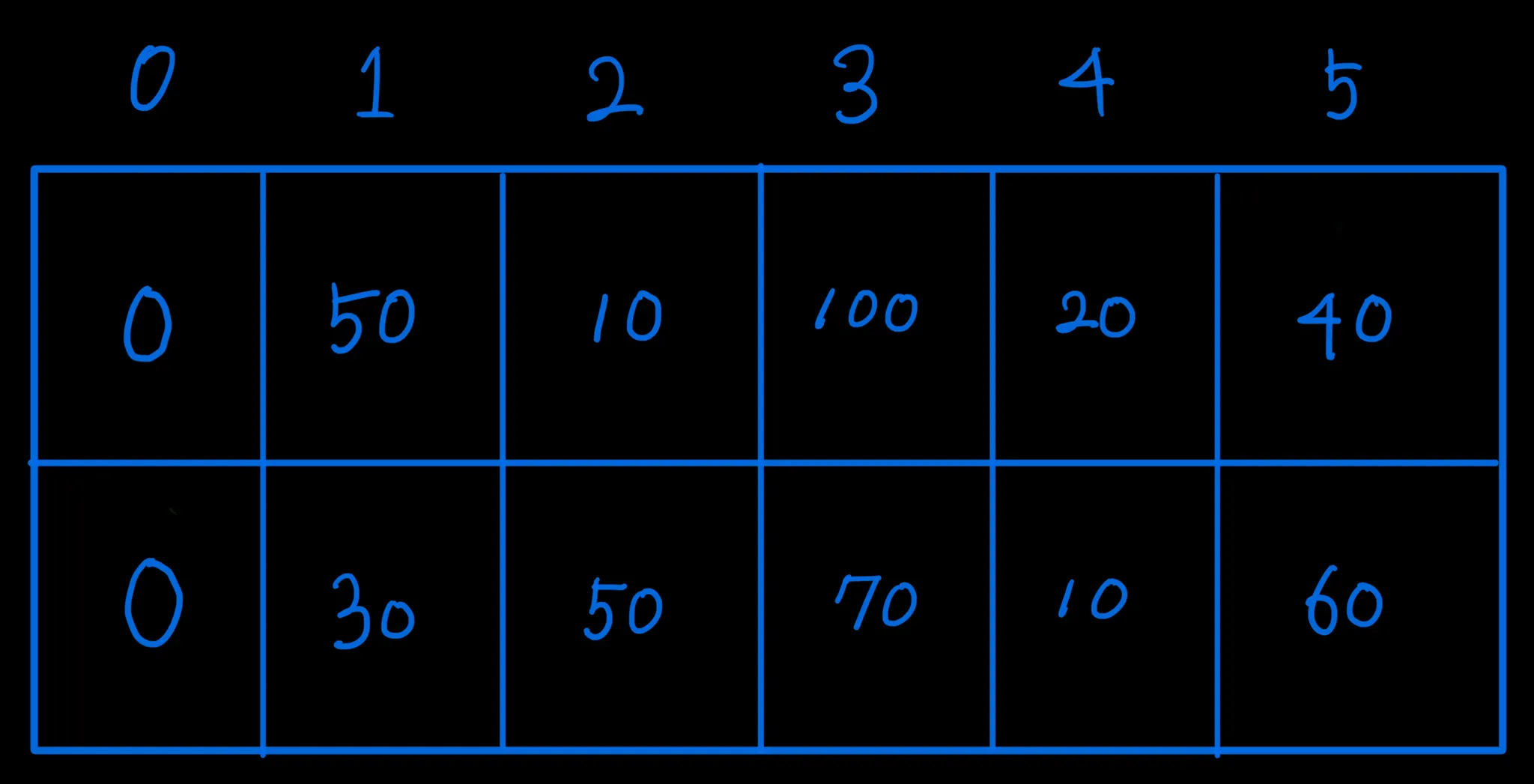
스티커 문제는 2행 n열로 배치된 스티커 판이 있고 스티커 한 장을 떼면 그 스티커와 변을 공유하는 스티커는 찢어져 사용할 수 없게 된다. 각 스티커 마다 점수를 매겨 땔수 있는 스티커 점수의 최대값을 구하는 문제이다.
처음 접근 시에 아래와 같이 뗄 수 있는 스티커 경우의 수의 모습을 그려보았다.
총 4가지 경우로 스티커를 뗄 수 있으며 점수를 비교해 가며 이중배열에 더해가는 점화식으로 구현하였다.
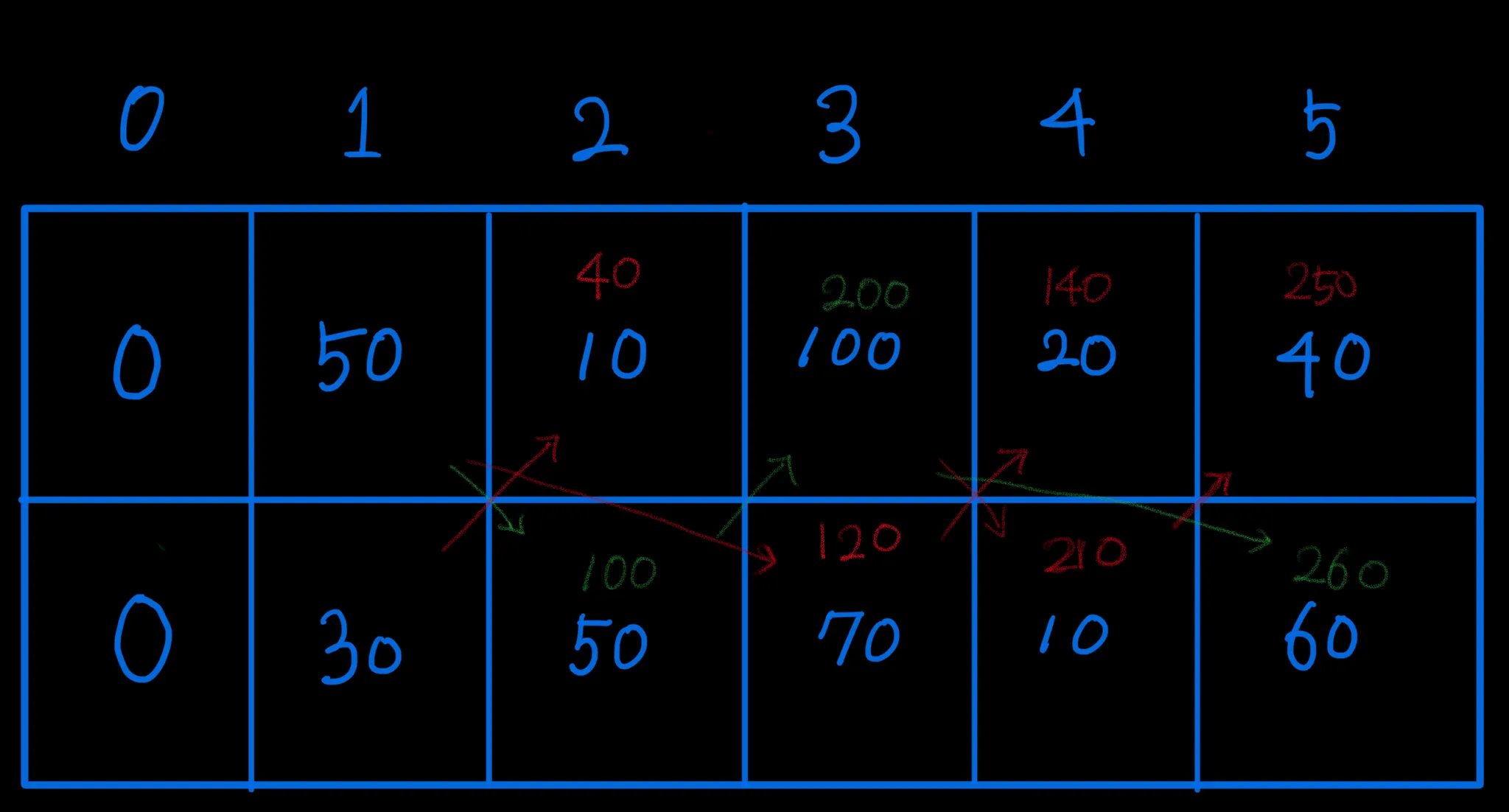
아래의 그림처럼 arr[0][0] / arr[1][0]을 첫인덱스비교를 위해 0으로 초기화 해준뒤 j - 1 과 j - 2 중 더 높은 수를 더해 가는 방식으로 두 방향으로 이중 배열에 값을 넣어주었다.
그리하여 현재 인덱스의 값은 이전 인덱스 중 가능한 패턴의 높은 값의 합이다.
마지막 인덱스까지 비교하여 넣었을때 arr[0] or arr[1] 두개의 마지막 인덱스 중 큰 수를 가지고 있는 배열값을 출력하는 것으로 구현하였다.
2. 코드
#include <iostream>
#include <algorithm>
#include <cstdio>
using namespace std;
int main()
{
int k;
int line;
//케이스 개수
cin >> k;
for (int i = 0; i < k; i++)
{
//라인 인덱스 수
scanf("%d", &line);
//이중 배열 선언
int arr[2][line + 1];
//0번쨰 인덱스 0 초기화
arr[0][0] = 0;
arr[1][0] = 0;
//스티커 점수 배열에 저장
for (int a = 1; a < line + 1; a++)
scanf("%d", &arr[0][a]);
for (int b = 1; b < line + 1; b++)
scanf("%d", &arr[1][b]);
// 2번 인덱스 부터 가능한 수 비교 하며 더해감
for (int j = 2; j < line + 1; j++)
{
arr[0][j] += max(arr[1][j - 1] , arr[1][j - 2]);
arr[1][j] += max(arr[0][j - 1] , arr[0][j - 2]);
}
// 더 높은 라인의 값 출력
printf("%d\n", max(arr[0][line],arr[1][line]));
}
return 0;
}
C++
복사
3. 채점 기록
메모리 : 2672KB / 시간 : 136ms