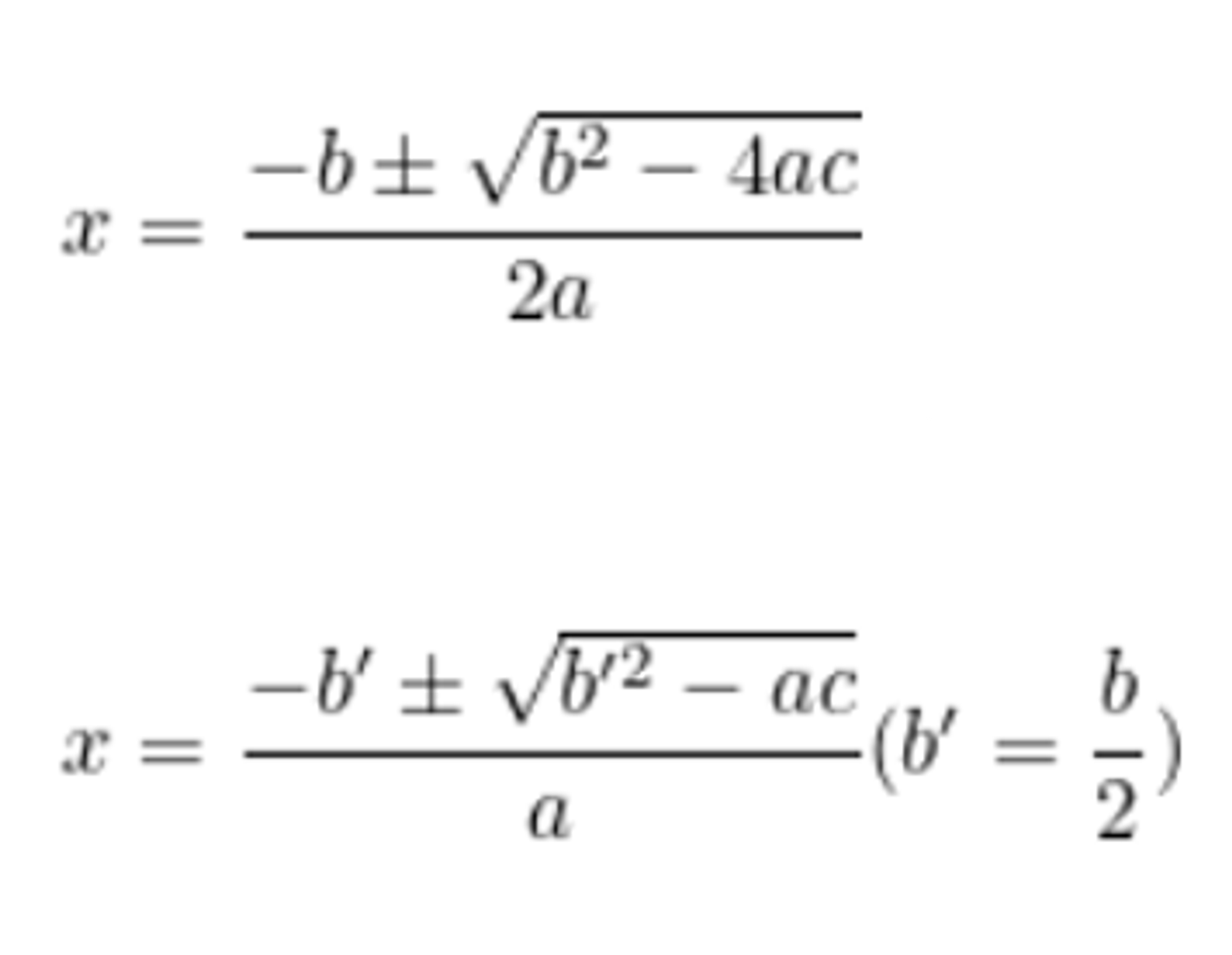궁금한 내용, 오타, 수정사항, 문의사항은 아래 깃허브 이슈 혹은 노션 블록 댓글로 달아주시면 바로 확인해드립니다! 도움이 되셨다면 아래 링크를 통해  한번 꾹 눌러주세요
한번 꾹 눌러주세요 
6. HIT RECORD
이번 장에서는 광선이 오브젝트를 hit했을 때의 정보(교점의 위치와 albedo, 교점에서의 법선 등)를 저장할 hit_record라는 구조체에 대해 알아볼 것이다.
6.1. 실습목표
hit_record 구조체에 대해 알아보고 구조체를 만든다.
6.2. hit record
4단원과 5단원에서 작성했던 hit_sphere함수의 return 값에 대해 생각해보자. 4단원에서는 hit_sphere 함수는 광선이 구를 hit했는지 아닌지를 확인할 수 있는 값을 return 했고, 5단원에서는 primary ray의 origin과 교점 사이의 거리에 해당하는 값을 return 했다.
하지만 hit했는지 아닌지 여부만으로는 충분하지 않다. origin과 교점 사이의 거리만으로도 부족하다. 광선을 추적하고 이미지를 렌더링하기 위해서는 더 많은 정보가 필요하다. 우선 교점의 정확한 위치가 필요하다. 교점의 위치를 알아야 교점에서의 법선 벡터를 알 수 있고, 법선 벡터를 알아야 광원이 오브젝트에 미치는 영향을 계산할 수 있다. 그러므로 이러한 정보들을 저장할 구조체가 필요하다.
다음과 같은 구조체를 만들어서 structures.h에 추가해주자.
...
///추가
typedef struct s_hit_record t_hit_record;
...
///추가
struct s_hit_record
{
t_point3 p;
t_vec3 normal;
double tmin;
double tmax;
double t;
t_bool front_face;
};
C
복사
Code1 : [miniRT/include/structures.h]
p는 교점의 좌표, normal은 교점에서의 법선, t는 광선의 원점과 교점 사이의 거리이다. tmin과 tmax, front_face가 무엇인지, 왜 필요한지는 이번 장에서 더 설명할 것이다. 교점에서의 색깔 등 추가적으로 필요한 정보는 교재를 따라가며 필요할 때 t_hit_record 구조체 안에 추가해주도록 하자.
6.3. hit record 적용
hit 했을 때의 정보를 저장할 hit record 구조체를 만들었으니 적용을 해보자.
...
t_color3 ray_color(t_ray *ray, t_sphere *sphere)
{
double t;
t_vec3 n;
//추가
t_hit_record rec;
rec.tmin = 0;
rec.tmax = INFINITY;
//추가 끝
//제거
t = hit_sphere(sphere, ray);
if (t > 0.0)
{
n = vunit(vminus(ray_at(ray, t), sphere->center));
return (vmult(color3(n.x + 1, n.y + 1, n.z + 1), 0.5));
}
//제거 끝
//추가
if (hit_sphere(sphere, ray, &rec))
return (vmult(vplus(rec.normal, color3(1, 1, 1)), 0.5));
//추가 끝
...
C
복사
Code2 : [miniRT/src/trace/ray/ray.c]
tmin과 tmax는 무엇일까? 우리는 광선 벡터를 t에 관한 매개 방정식
P(t) = O + t * D
으로 나타내기로 했고, t는 광선 벡터의 크기라고 했다. O는 광선의 출발점, 즉 카메라의 위치이다. t가 0보다 작다는 것은 방향이 음수이고, 광선이 뒤를 향하고 있다는 것이다. 우리는 카메라의 뒤에 있는 오브젝트는 고려할 필요가 없다. tmin과 tmax의 값은 각각 0과 INFINITY로 오브젝트가 카메라의 뒤에 있거나(t < 0), 오브젝트가 카메라로부터 너무 멀 경우를 고려해주기 위함이다.
hit_sphere함수의 인자로 hit record 구조체를 넘겨주었다. 이번엔 hit_sphere 함수를 수정해보자. 아래 코드는 수정된 부분이 많아서 설명을 돕기 위해 함수 내부에서 줄마다 번호를 달아두었다. 수정된 부분에 대한 설명은 아래에서 이어나갈 것이다.
#include "structures.h"
#include "utils.h"//추가
#include "trace.h"//hit_sphere는 관련 정보를 hit_record에 저장하고 TRUE & FALSE를 반환하므로,
//double hit_sphere(t_sphere *sp, t_ray *ray)를 아래와 같이 변경
//typedef int t_bool; TRUE or FALSE를 return하는 함수를 표현하기 위해 t_bool 사용
t_bool hit_sphere(t_sphere *sp, t_ray *ray, t_hit_record *rec)
{
1 t_vec3 oc;
2 double a;
3 // double b; b를 half_b로 변경
4 double half_b;
5 double c;
6 double discriminant; //판별식
7 //추가
8 double sqrtd;
9 double root;
10
11 oc = vminus(ray->orig, sp->center);
12 //제거
13 a = vdot(ray->dir, ray->dir);
14 b = 2.0 * vdot(oc, ray->dir);
15 c = vdot(oc, oc) - sp->radius2;
16 discriminant = b * b - 4 * a * c;
17 if (discriminant < 0) // 판별식이 0보다 작을 때 : 실근 없을 때,
18 return (-1.0);
19 else
20 return ((-b - sqrt(discriminant)) / (2.0 * a)); // 두 근 중 작은 근
21 //제거 끝
22 //추가
23 a = vlength2(ray->dir);
23 half_b = vdot(oc, ray->dir);
24 c = vlength2(oc) - sp->radius2;
26 discriminant = half_b * half_b - a * c;
27
28 if (discriminant < 0)
29 return (FALSE);
30 sqrtd = sqrt(discriminant);
31 //두 실근(t) 중 tmin과 tmax 사이에 있는 근이 있는지 체크, 작은 근부터 체크.
32 root = (-half_b - sqrtd) / a;
33 if (root < rec->tmin || rec->tmax < root)
34 {
35 root = (-half_b + sqrtd) / a;
36 if (root < rec->tmin || rec->tmax < root)
37 return (FALSE);
38 }
39 rec->t = root;
40 rec->p = ray_at(ray, root);
41 rec->normal = vdivide(vminus(rec->p, sp->center), sp->radius); // 정규화된 법선 벡터.
42 set_face_normal(ray, rec); // rec의 법선벡터와 광선의 방향벡터를 비교해서 앞면인지 뒷면인지 t_bool 값으로 저장.
43 return (TRUE);
44 //추가 끝
}
C
복사
Code3 : [miniRT/src/trace/hit/hit_sphere.c]
13 ~ 16 을 23 ~ 26과 바꾼 이유는, 근의 공식을 짝수 근의 공식으로 바꿔 계산을 단순히 하기 위함이다.
•
ax^2^ + bx +c = 0
•
ax^2^ + 2b'x +c = 0 (단, b' = b / 2)
위 두 2차 방정식의 근의 공식은 다음과 같다.(이미지1)
이미지1. 근의 공식, 짝수 근의 공식
30번부터 38번줄을 추가해 준 이유를 살펴보자.
30 sqrtd = sqrt(discriminant);
31 //두 실근(t) 중 tmin과 tmax 사이에 있는 근이 있는지 체크, 작은 근부터 체크.
32 root = (-half_b - sqrtd) / a; // 두 근(t) 중 작은 근(t)부터 고려.
33 if (root < rec->tmin || rec->tmax < root) 작은 t가 tmin보다 작거나 tmax보다 큰 경우
34 {
35 root = (-half_b + sqrtd) / a; 큰 근(t)가 tmin보다 작은지, tmax보다 큰지 체크.
36 if (root < rec->tmin || rec->tmax < root) 큰 근조차 tmin보다 작다면 hit하지 않은 것이므로 FALSE를 반환.
37 return (FALSE);
38 }
C
복사
광선이 오브젝트를 관통한다면 두 개의 교점이 생길 것이고, 카메라에는 가까운 교점에 해당하는 부분만 보일 것이다. 그런데 왜 두 교점을 모두 고려해줬을까? 어떤 구가 카메라를 둘러싸고 있다고 생각해보자. 그럼 두 근 중 작은 근은 카메라의 뒤쪽에 있는 것이고, 두 근 중 큰 근이 카메라의 앞에 있게 될 것이다. 위와 같은 경우를 고려해주기 위해 두 근을 모두 확인하는 것이다.
39 rec->t = root;
40 rec->p = ray_at(ray, root);
41 rec->normal = vdivide(vminus(rec->p, sp->center), sp->radius); // 정규화된 법선 벡터.
42 set_face_normal(ray, rec); // rec의 법선벡터와 광선의 방향벡터를 비교해서 앞면인지 뒷면인지 t_bool 값으로 저장.
43 return (TRUE);
C
복사
39 ~ 41은 hit record 구조체인 rec에 필요한 정보들을 저장하는 것이다.
42의 set_face_normal(ray, rec)은 위에서 언급한, 구가 카메라를 둘러싸고 있는 경우를 고려하기 위함이다. 카메라가 구의 안쪽에 있다면 광선과 법선은 같은 방향을 향하게 될 것이다. 그러나 오브젝트와 광원 간의 상호작용을 계산하기 위해서는 법선과 광선이 항상 반대방향을 향하고 있어야 한다. 그러므로 법선이 광선을 반대 방향인지를 확인하는 함수를 추가했다.
#include "trace.h"
void set_face_normal(t_ray *r, t_hit_record *rec)
{
// 광선의 방향벡터와 교점의 법선벡터의 내적이 음수이면 광선은 앞면(객체의)에 hit 한 것이다
rec->front_face = vdot(r->dir, rec->normal) < 0;
// 광선의 앞면에 hit 면 그대로 아니면 법선을 반대로 뒤집는다. (항상 광선 방향벡터와 법선 벡터를 반대인 상태로 사용하기위해)
rec->normal = (rec->front_face) ? rec->normal : vmult(rec->normal, -1);
}
C
복사
Code4 : [miniRT/src/trace/hit/normal.c]
지금까지 변경 또는 추가한 함수를 헤더 파일에 반영해주자.
...
// trace/hit/
//double hit_sphere(t_sphere *sp, t_ray *ray); 아래로 변경
t_bool hit_sphere(t_sphere *sp, t_ray *ray, t_hit_record *rec);
void set_face_normal(t_ray *r, t_hit_record *rec);
#endif
C
복사
Code5 : [miniRT/include/trace.h]
코드 수정 후 출력 결과물은 05번과 같아야 한다. 혹시 결과가 다르다면 다르게 작성한 부분이 있는지 확인해보자. 다음 장에서는 한 광선이 여러개의 물체를 지나는 경우를 생각해보자.