Raytracing in one weekend 식 이해하기 2
이번 시간에는 Ray를 계산하는 식들에 대해 알아볼 예정이다! 영어도 엄청 길게 써져있고 어려워 보이지만 생각보다 간단하다! 차근차근 식을 보면서 코드를 이해해보자!
이번 챕터를 이해하면 아래의 화면을 만들 수 있다!!
The ray Class
ray클래스는 ray에 대한 이해를 하면 어떤 것들이 필요한지 간단하게 알 수 있다. 우리가 특정 지점에서 목표지점으로 하나의 ray(즉, 벡터)를 쏘고 싶다면 이전에 배운것과 같이 벡터 연산을 활용할 수 있다. 생성자에 대한 설명은 생략하겠다.
1) ray의 성분
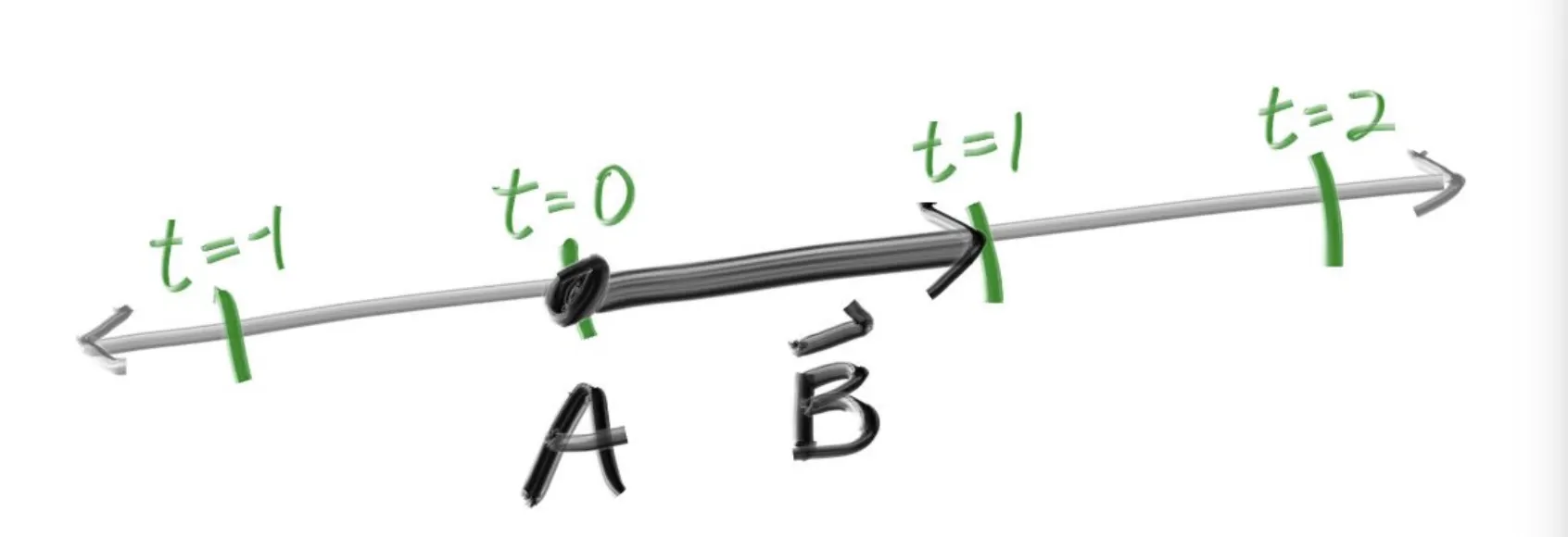
문서의 그림과 함께 살펴보자!
우리가 현재 A 지점에 있고 t = 1 방향으로 ray를 쏘고 싶다면 우리는 어떤 성분들을 가지고 있으면 될까?
바로 원점 A와 방향벡터 B이다!
class ray {
// member function
...
public:
point3 orig;
vec3 dir;
};
C++
복사
•
point3 orig : 원점 좌표 (A)
•
vec3 dir : 방향벡터 (B)
여기서 우리는 orig이 벡터가 아니라 3차원 상의 원점 좌표임을 이해해야 한다! 즉 우리가 ray를 만들고 싶다면 원점좌표 orig에서 t의 크기만큼 dir방향으로 뻗어나가는 벡터임을 알아야 한다.이 식을 멤버함수로 만든것이 바로 아래의 코드이다. 이 식을 계산한 결과는 바로 우리가 원점orig에서 dir방향으로 t만큼 이동한 곳의 3차원상의 좌표가 나와야 하기 때문에 point3형을 반환해야 한다!
// C++
// 여기서 orig 은 3차원 상의 좌표, dir 은 방향벡터이다!
point3 at(double t) const {
return orig + t*dir;
}
C++
복사
C에서는 구조체와 구조체의 더하기를 연산자로 할 수 없기 때문에 하나하나 성분의 합을 구해주어야 한다.
// C
t_vec ray_at(t_ray *ray, double t)
{
t_vec out;
out.x = ray->origin.x + ray->dir.x * t;
out.y = ray->origin.y + ray->dir.y * t;
out.z = ray->origin.z + ray->dir.z * t;
return (out);
}
C
복사
2) Sending Rays Into the Scene
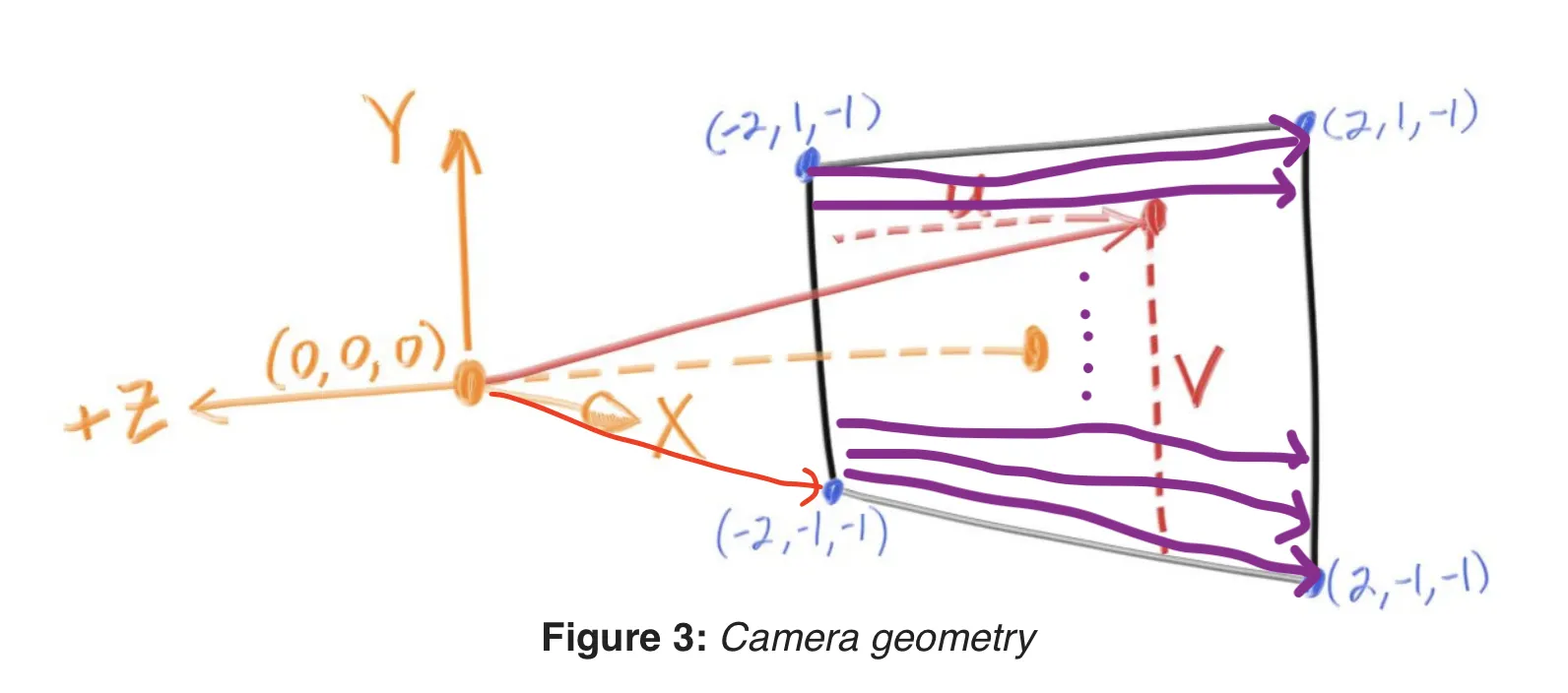
이제 우리는 화면에 ray를 쏠 것이다! 아래 그림을 보자!
간단하게 3차원 좌표로 생각했을 때 x, y, z 축은 아래 화살표와 같은 방향으로 뻗어나가고 있다.
우리는 원점 (0, 0, 0)에서 screen으로 ray를 쏴서 ray가 맞은 점 P를 구할 것이다. 이후 그 점의 색을 가져와 우리가 만든위치에 표현할 것이다. 차근차근 위에서 부터 살펴보자!
color ray_color(const ray& r)함수는 마지막에 보도록 하겠다!
우선 우리가 표현할 이미지의 비율과 가로 길이를 가져온다.
// C++ code
// Image
const auto aspect_ratio = 16.0 / 9.0;
const int image_width = 400;
const int image_height = static_cast<int>(image_width / aspect_ratio);
// Camera
auto viewport_height = 2.0;
auto viewport_width = aspect_ratio * viewport_height;
auto focal_length = 1.0;
C++
복사
C++로 적혀있는 변수들을 C로 바꾸어보자!
// C code
// Image
double aspect_ratio = 16.0 / 9.0;
int image_width = 400;
int image_height = (int)((double)image_width / aspect_ratio);
// Camera
double viewport_height = 2.0;
double viewport_width = aspect_ratio * viewport_height;
double focal_length = 1.0;
C
복사
•
aspect_ratio : 화면 비율을 나타낸다!
•
image_width : 우리가 생성할 이미지의 너비이다
•
image_height : 우리가 생성할 이미지의 높이이다.
•
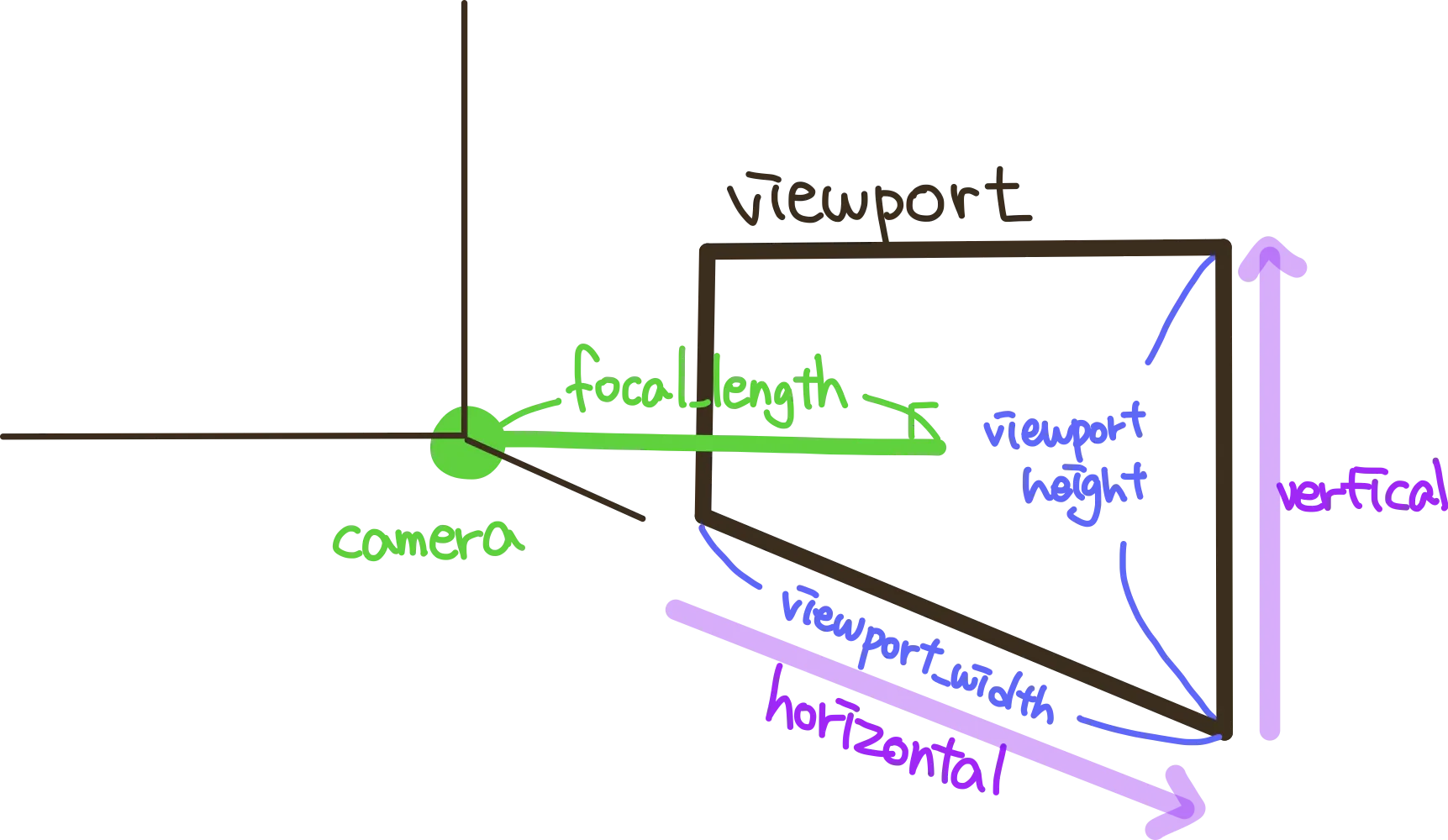
viewport_height : 우리가 ray를 쏘는 기준인 viewport의 높이이다!
•
viewport_height : 우리가 ray를 쏘는 기준인 viewport의 너비이다!
•
focal_length : 우리가 ray를 쏠 위치와 viewport까지의 최단거리이다. 즉 viewport의 중점과 ray의 원점을 이은 거리이다.
이제 아래 선언된 벡터들을 코드 아래 사진과 함께 보자!!
•
origin은 ray를 쏘는 원점이다.
•
horizontal은 +x축 방향을 가지며 크기가 viewport_width인 벡터이다.
•
vertical은 +y축 방향을 가지며 크기가 viewport_height인 벡터이다.
•
vec3(0, 0, focal_length) 는 +z축 방향을 가지며 크기가 focal_length인 벡터이다.
// C++ code
auto origin = point3(0, 0, 0);
auto horizontal = vec3(viewport_width, 0, 0);
auto vertical = vec3(0, viewport_height, 0);
auto lower_left_corner = origin - horizontal/2 - vertical/2 - vec3(0, 0, focal_length);
C++
복사
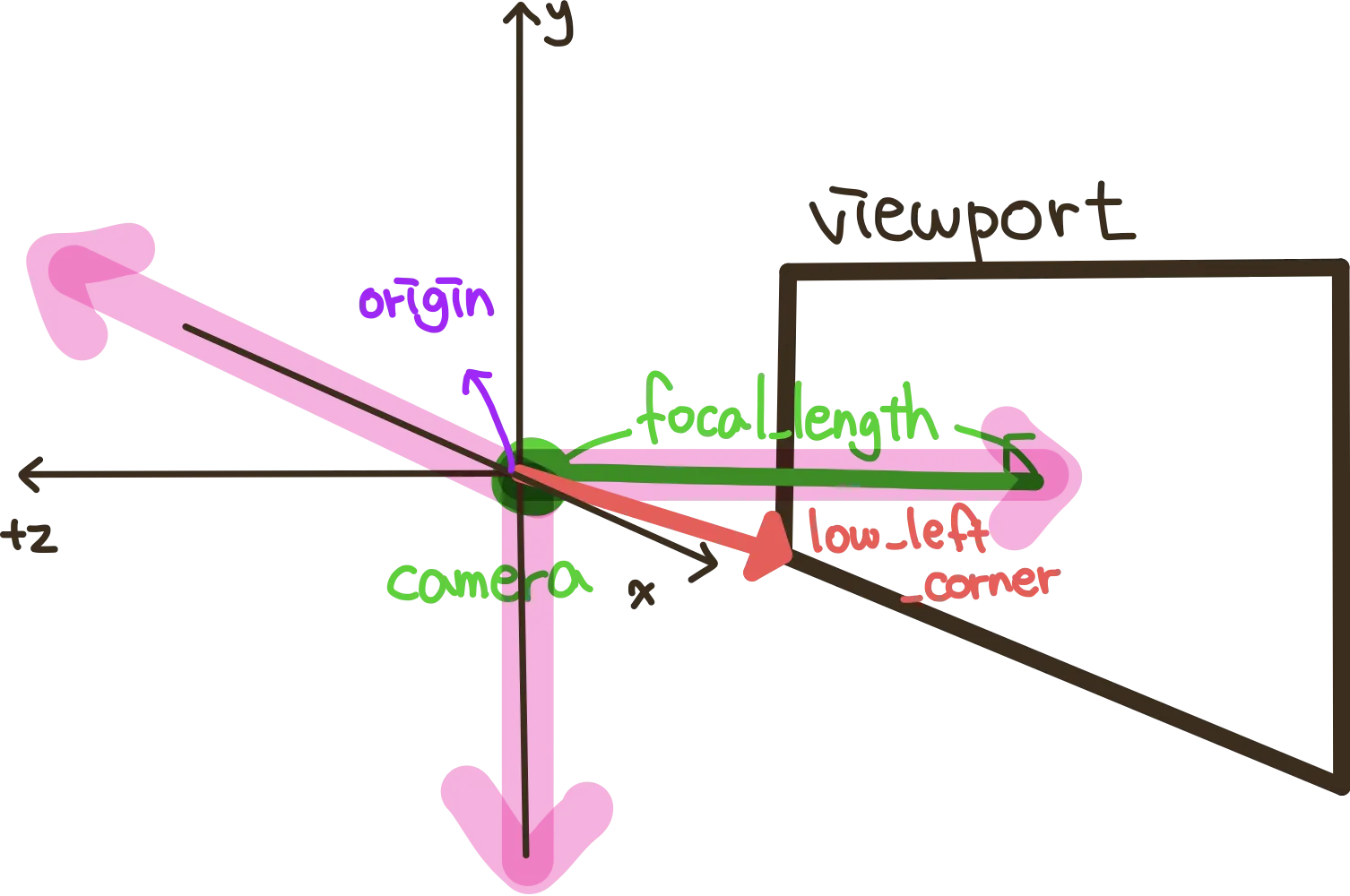
우리는 이 성분들을 활용해서 lower_left_corner을 구할 것이다!
lower_left_corner란 원점 (0, 0, 0)에서 viewport의 왼쪽 아래 꼭지점을 향하는 벡터이다. (빨간색 선)
이 벡터를 구하기 위해서는 핑크색 벡터 성분들을 모두 더해주면 된다!
(1)번 벡터는 camera에서 아래로 내려가는 벡터
(2)번 벡터는 camera에서 뒷쪽으로 뻗어가는 벡터
(3)번 벡터는 camera에서 viewport로 향하는 벡터
camera에서 아래로 내려가는 벡터는 이다. 왜 이렇게 되는지 살펴보자. 현재 vertical 벡터는 아래와 같이 선언되어있다.
// C++
auto vertical = vec3(viewport_height, 0, 0);
// C
t_vec vertical = vec(viewport_height, 0, 0);
C++
복사
viewport_height 는 2이기 때문에 vec3(0, 2, 0)인 것을 알 수 있다! 원점이 화면의 중앙에 있기 때문에 우리는 크기가 절반인 벡터가 필요하다. 즉, vec3(0, 1, 0). 하지만 이 벡터는 x축이 양수인 방향을 향하고 있다. 이제 이 벡터를 뒤집어 주기만 하면 된다. 우리는 이전에 역벡터를 구하는 방법을 배웠다. 바로 모든 성분에 -를 해주면 된다! vec3(0, -1, 0).
결과적으로 우리가 필요한 벡터는 vec3(0, -1, 0). 즉, (-vertical / 2) 이다. 이제 우리가 필요로하는 1번 벡터를 구했다. 마찬가지 방법으로 2, 3번 벡터도 구할 수 있다.
•
(2)번 벡터 = vec3(0, -1, 0) ⇒ (-horizontal / 2)
•
(3)번 벡터 = vec3(0, 0, -1) ⇒ (-focal_length / 2)
이제 lower_left_corner 를 구할 준비가 끝났다. 벡터의 법칙에 의해 (1), (2), (3) 번 벡터를 모두 더해주기만 하면 된다!
이제 벡터의 성분을 알았으니 ray를 쏠 카메라의 위치에 더해주기만 하면 된다.
(지금은 원점이 (0, 0, 0)이기 때문에 영향을 주지 않는다!)
// C++
auto lower_left_corner = origin - horizontal/2 - vertical/2 - vec3(0, 0, focal_length);
C++
복사
// C
t_vec lower_left_corner =
vec(origin.x + (- horizontal.x / 2) + (-vertical.x / 2) + (0)
,origin.y + (- horizontal.y / 2) + (-vertical.y / 2) + (0)
,origin.z + (- horizontal.z / 2) + (-vertical.z / 2) + (-focal_length));
C
복사
그렇다면 왜 lower_left_corner 벡터를 구하는 것일까?
이제 우리는 이 벡터에 U, V 벡터를 더하면서 왼쪽 아래 꼭지점부터 오른쪽 위 꼭지점까지 ray를 쏠 것이다!!
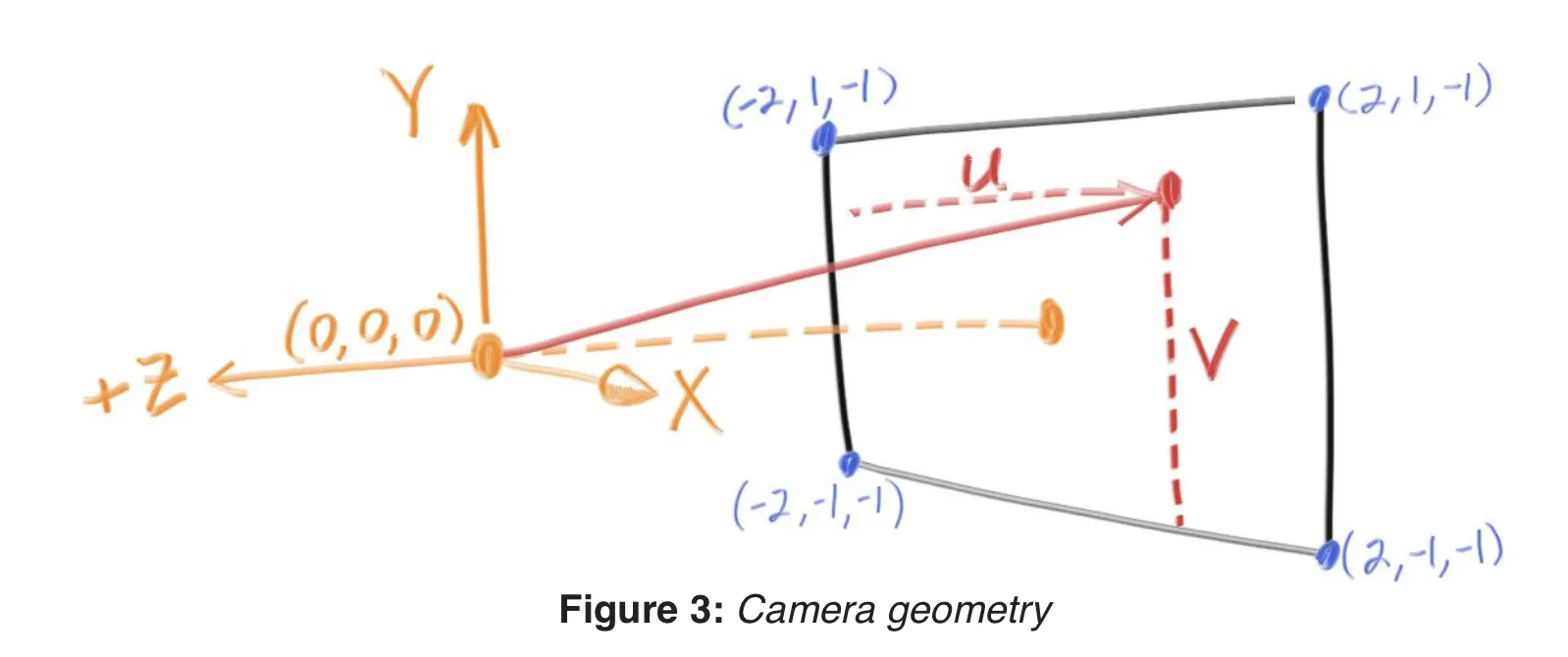
즉, 아래 화면의 (-2, -1, -1)에서 시작해서 (2, 1, -1) 까지 반복문을 돌게 된다!
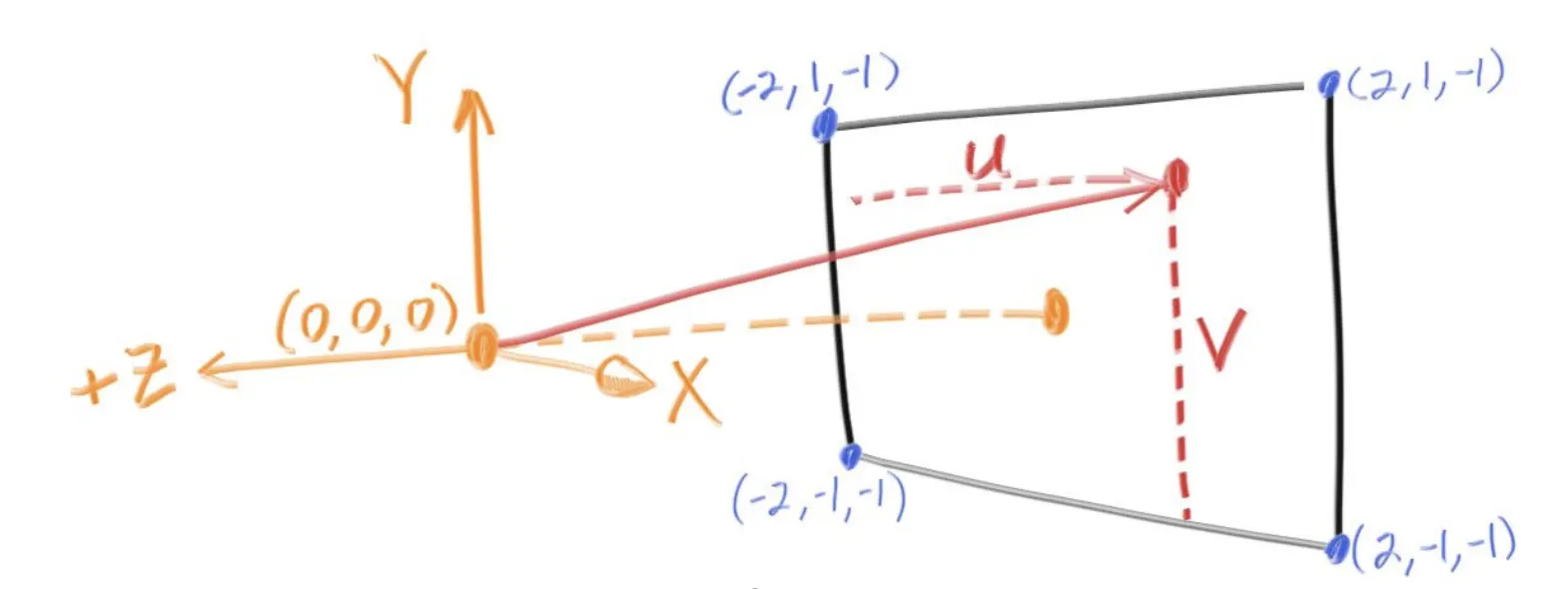
아래 그림을 보자! 위 그림의 viewport를 향하는 벡터는 우리가 구한 lower_left_corner벡터에 x축성분에 u만큼, y축 성분에 v만큼 이동한 벡터이다!
본문에는 아래와 같이 코드가 나와있다.
// C++
// u, v는 스칼라 값이다!
ray r(origin, lower_left_corner + u*horizontal + v*vertical - origin);
// C
t_ray r;
r.origin = vec(0, 0, 0); // 3차원상의 정점 좌표
r.dir = // 방향벡터
vec(lower_left_corner.x + u*horizontal.x + v*vertical.x - origin.x,
lower_left_corner.y + u*horizontal.y + v*vertical.y - origin.y,
lower_left_corner.z + u*horizontal.z + v*vertical.z - origin.z);
C++
복사
이 코드를 풀어서 이해해보면 말 그대로 lower_left_corner 벡터를 원하는 성분만큼 이동시킨 것이다! 아래 코드를 보면 u와 v는 image_width, image_heigth값을 나눠서 계산한 0 ~ 1 사이의 값인 것을 알 수 있다!
for (int j = image_height-1; j >= 0; --j) {
for (int i = 0; i < image_width; ++i) {
auto u = double(i) / (image_width-1);
auto v = double(j) / (image_height-1);
ray r(origin, lower_left_corner + u*horizontal + v*vertical - origin);
}
}
C++
복사
결과적으로
u * horizontal 연산을 한 후의 벡터는 (-1, 0, 0) ~ (1, 0, 0)의 값을 순차적으로 가지게 되고
v * vertical 연산을 한 후의 벡터는 (0, -1, 0) ~ (0, -1, 0)의 값을 순차적으로 가지게 되는 것이다.
이제 우리는 이렇게 나온 ray 벡터들을 가지고 색을 가져와 볼 것이다.
color ray_color(const ray& r) {
vec3 unit_direction = unit_vector(r.direction());
auto t = 0.5 * (unit_direction.y() + 1.0);
return (1.0 - t)*color(1.0, 1.0, 1.0) + t * color(0.5, 0.7, 1.0);
}
C++
복사
코드의 첫 줄부터 살펴보자!!!
1.
ray가 가지고있는 방향벡터의 단위벡터를 가지고 온다! (왜 단위벡터를 가지고 올까?? 이유는 아래에!!)
// C++
vec3 unit_direction = unit_vector(r.direction());
C++
복사
unit_direction은 벡터 r 의 방향벡터(r.dir)을 벡터의 크기로 나눈 것이다. 이코드는 아래와 같이 C로 구현할 수 있다.
t_vec vec_unit(t_vec v)
{
double len;
len = vec_length(v);
return (vec(v->x / len
,v->y / len
,v->z / len));
}
C++
복사
즉 다음과 같이 쓸 수 있다.
// C
t_vec unit_direction = vec_unit(r.dir);
C++
복사
이렇게 단위백터를 가져와서 우리는 방향은 있지만 크기가 1인 벡터를 가져올 수 있는 것이다!!2.
두번째 줄은 위에서 구한 단위벡터의 y값에 따라 t를 만들어 줄 것이다!
위에서 우리는 ray벡터를 단위벡터로 바꿔주었기 때문에 y의 범위가 -1 부터 1사이이다!
우리는 이 벡터를 활용해서 color을 구해야 하는데 color에는 음수값이 없다!
auto t = 0.5 * (unit_direction.y() + 1.0);
C++
복사
위의 식에서는 1을 더해서 0 ~ 2값을 만들어 준 후 2 를 나눠서 0 ~ 1 사이의 double 값을 만들어 준 것이다!! 이렇게 되면 대략 이런 형태의 출력을 얻을 수 있다! (아래의 출력 결과는 최종 결과가 아니다!! 참고용으로 만든 텍스트이다!
// y의 값이 증가할수록 숫자가 커진다!!
55555555555555
44444444444444
33333333333333
22222222222222
11111111111111
00000000000000
C++
복사
3.
마지막 부분은 t값에 따라 바뀌는 색을 표현한 것이다!
return (1.0 - t)*color(1.0, 1.0, 1.0) + t * color(0.5, 0.7, 1.0);
C++
복사
•
R :
•
G :
•
B :
즉 B값은 항상 1이고 나머지 R, G값을 조금씩 줄여가는 것을 알 수 있다!! 이러한 식을 활용해서 출력을 하게되면 아래와 같은 화면이 나오게 된다!
