Raytracing One Weekend 식 이해하기! 3
이번 시간에는 화면의 가운데 구를 띄워볼 것이다!!
이 과제를 진행하기 위해서는 우선 근의 공식에 대한 이해가 필요하다! 차근차근 아래 내용을 따라가보자!
Adding a Sphere
이 부분은 책에서 유도하는 방식을 차근차근 따라가보자!
1) 구 방정식
3차원 좌표에서 구를 표현하는 방정식은 아래와 같다.
여기서 만약 구의 좌표가 C (x, y, z)에 있다면 아래와 같은 식을 얻을 수 있다. 이때 C는 point3클래스이다. C언어로 번역한 코드로 생각하면 t_vec클래스 변수인 것이다!
여기서 x, y, z는 구위의 한 지점들이다! 이때 구위의 한 좌표 (x, y, z)에서 중앙 (C.x, C.y, C.z) 까지의 벡터를 구하면,
같은 벡터를 내적하면 해당 벡터 크기의 제곱이 되므로 (여기서 * 은 내적이다!)
아래부터 이해하기 어려운 식이 나오는데 우선 아래 식에 대한 이해가 필요하다.
•
A : 원점 좌표
•
b : 방향벡터
•
t : 벡터의 크기(길이)
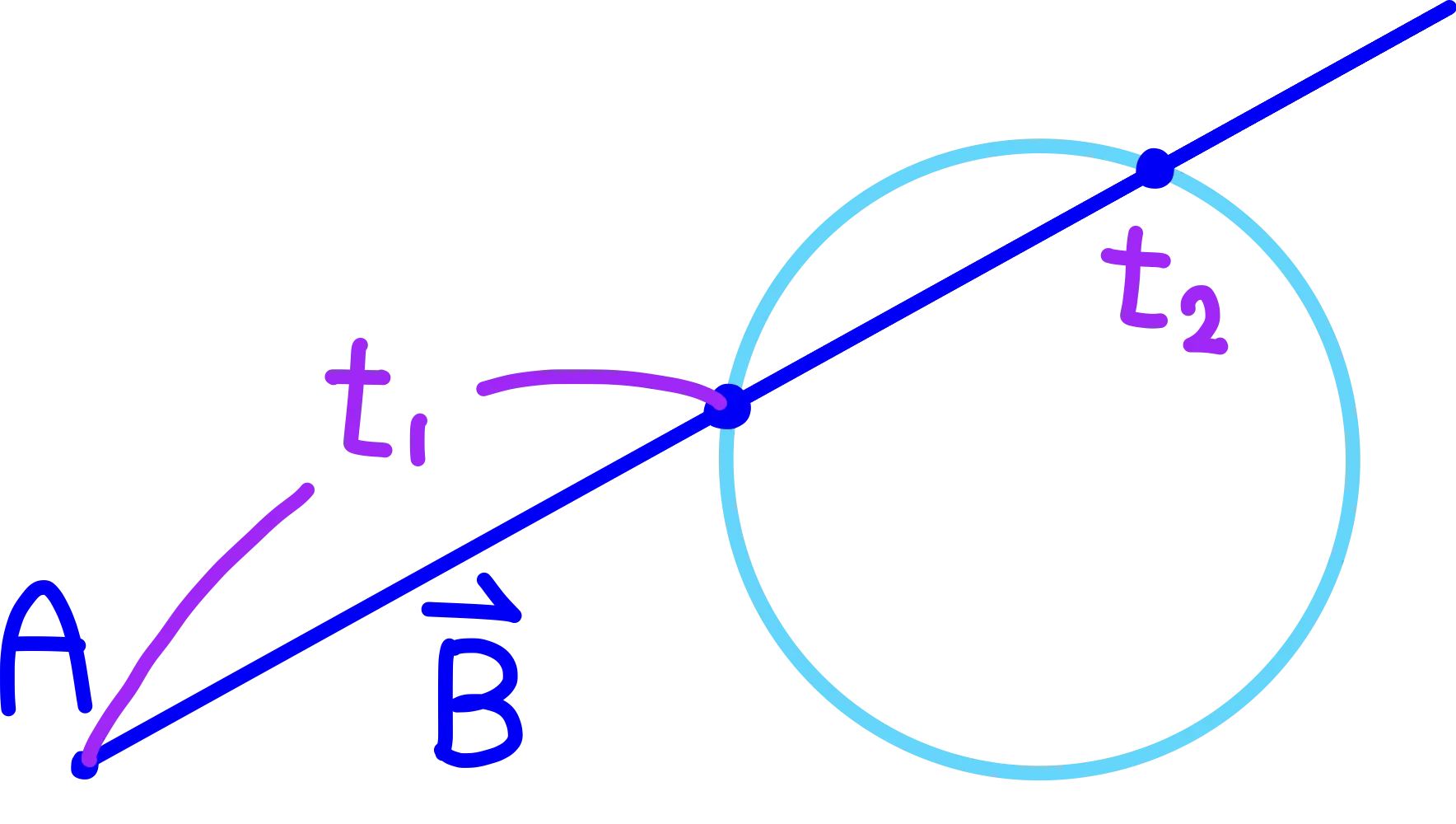
아래 그림처럼 우리가 정점 A에서 ray를 쏜다고 생각해보자. 이때 좌표상의 구에 우리가 쏜 ray와 부딪힌 지점들이 있을 것이다! 이때 t의 값은 바로 부딪힌 지점과 정점 A사이의 크기이다.
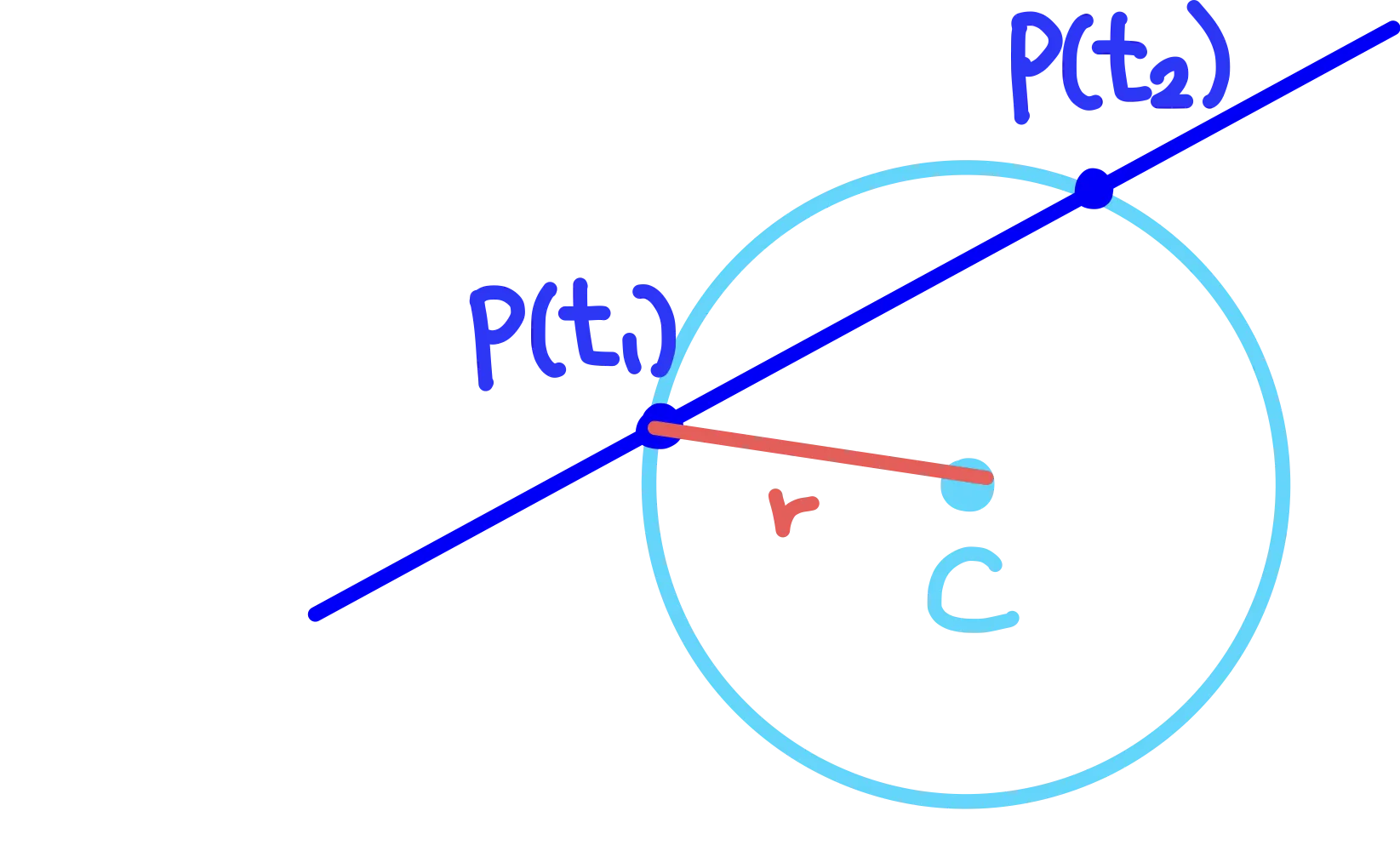
그렇다면 계속 이어나가보자. 우리는 우리의 ray가 구에 맞았는지를 알고 싶다. 위의 P - C 에서 P가 구위의 정점 좌표들을 나타내는 것이므로 우리는 여기에 우리 ray를 쐈을때 맞았는지를 확인하고 싶은 식을 넣으면 아래와 같이 되는 것이다. (C는 구의 중점의 정적 좌표이다!)
이 식의 결과로 해가 존재한다면 우리가 쏜 ray가 구 위에 있다는 것을 알 수 있다!!!
우리는 카메라의 위치는 A(정점좌표)를 알고 있고, ray를 쏘는 방향 b(방향벡터)를 알고 있다. 그리고 구 중앙의 정점좌표인 C와 구의 직경인 r을 모두 알고있다.
따라서 우리가 모르는 변수는 t이고 t에대한 식으로 위의 식을 정리해보면 아래와 같이 나오는 것이다.
근의 공식을 이해하기 쉽게 식의 순서를 조금 바꾸었다. 우리는 여기서 t값을 구해야하는데 2차방정식의 해를 구하는 방법은 바로 근의 공식을 사용하는 것이다.
만약 위와 같은 식이 있다면 x의 값은
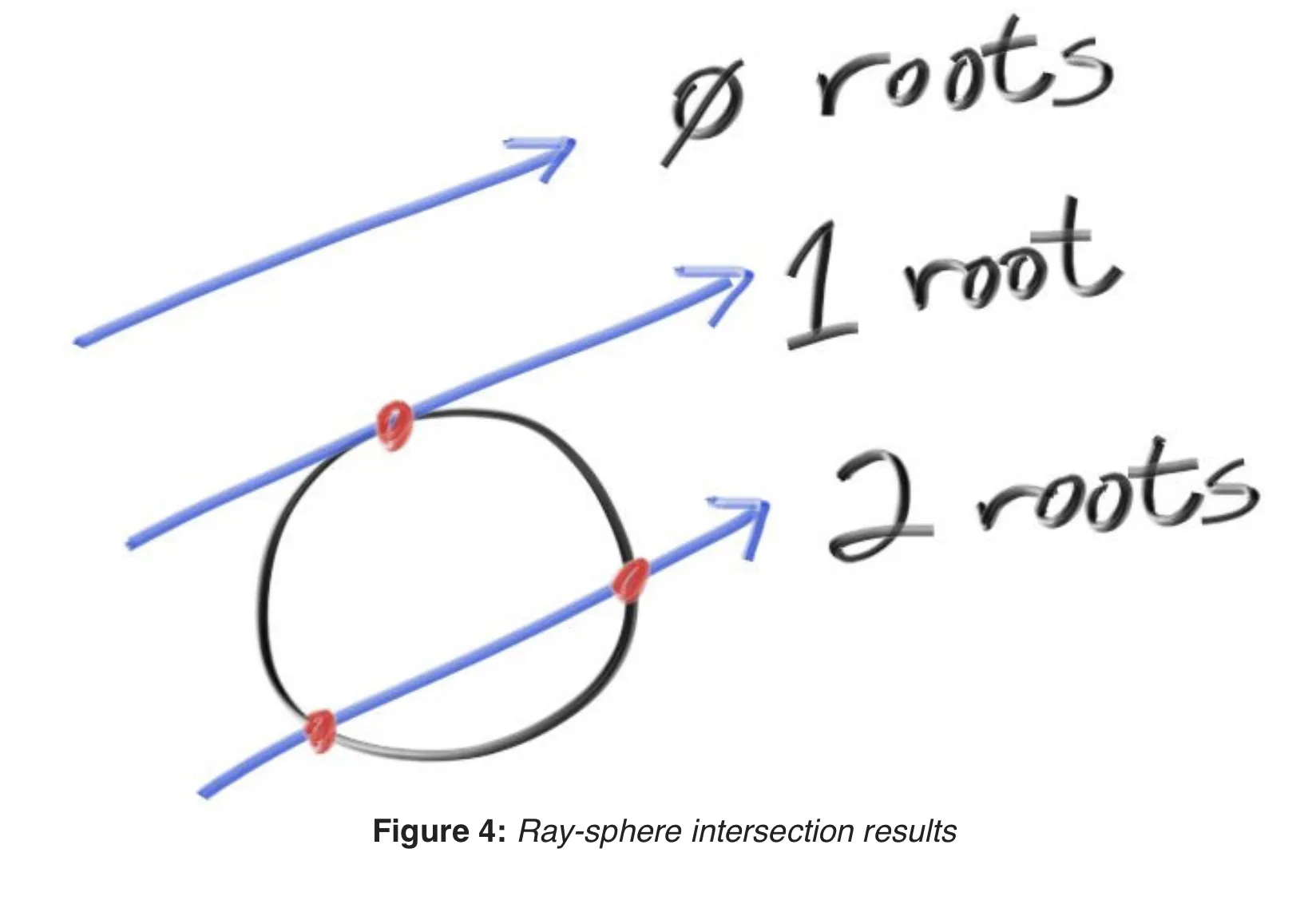
우리는 이 식을 바로 코드로 만들어 볼 것이다. 그 전에 x의 해에 대한 이해가 필요하다. 그림을 보면 현재 카메라에서 쏜 ray가 구를 만나는 지점들이 있을 것이다!
•
구와 부딪히는 지점이 없다면 : 해가 없다
•
구와 부딪히는 지점이 하나라면 : 해가 1개
•
구와 부딪히는 지점이 둘이라면 : 해가 2개
Creating Our First Raytraced Image
이제 그대로 근의 공식을 코드로 작성해보자. 아래 함수는 근의 공식을 활용해서 좌표상의 구와 우리가 쏜 ray의 점이 부딪히는지 부딪히지 않는지 판단해주는 코드이다
//C++
bool hit_sphere(const point3& center, double radius, const ray& r) {
vec3 oc = r.origin() - center;
auto a = dot(r.direction(), r.direction());
auto b = 2.0 * dot(oc, r.direction());
auto c = dot(oc, oc) - radius*radius;
auto discriminant = b*b - 4*a*c;
return (discriminant > 0);
}
C++
복사
여기서 우리가 의 결과가 0보다 크면 true를 return 하고 아니면 false를 return 하는 것을 알 수 있다. 왜 그런 것 일까?
위 근의 공식을 다시 자세히 보면 가 0이하의 수가 나오게 된다면 해가 나오지 않게 된다! 해가 없다면 우리는 우리가 쏜 ray가 구와 맞지 않는다는 것을 의미하기 때문에 false를 return 하는 것이다.
위 코드를 C로 변경한 결과이다.
//C
int hit_sphere(t_vec center, double radius, t_ray r) {
vec3 oc = vec(r.origin.x - center.x
,r.origin.y - center.y
,r.origin.z - center.z);
double a = vec_dot(r.direction(), r.direction());
double b = 2.0 * vec_dot(oc, r.direction());
double c = vec_dot(oc, oc) - radius * radius;
double discriminant = b * b - 4 * a * c;
if (discriminant > 0)
return (1);
return (0);
}
C++
복사
아래의 ray_color식은 이전 시간에 작성했던 코드와 많이 비슷하다.
color ray_color(const ray& r) {
if (hit_sphere(point3(0,0,-1), 0.5, r)) // 추가된 부분!!
return color(1, 0, 0); // 추가된 부분!!
vec3 unit_direction = unit_vector(r.direction());
auto t = 0.5*(unit_direction.y() + 1.0);
return (1.0-t) * color(1.0, 1.0, 1.0) + t * color(0.5, 0.7, 1.0);
}
C++
복사
아래에 색깔을 칠하는 부분에는 딱 두줄의 코드가 추가되었다! 바로 구와 만나서 위의 결과가 true가 나오게 된다면 빨간색을 칠하는 것이다! 아래 코드는 위 코드를 C로 바꾸어본 것이다.
// C code
t_vec color = vec(1, 0, 0);
t_vec center = vec(0, 0, -1);
if (hit_sphere(center, 0.5, r))
return (color);
C++
복사
color(1, 0, 0)을 해주는 이유는 책에서는 write_color함수에서 255.999를 곱해주기 때문이다! 즉, (1, 0, 0)을 넣으면 R : 255, G : 0, B : 0 인 색깔이 되는 것!