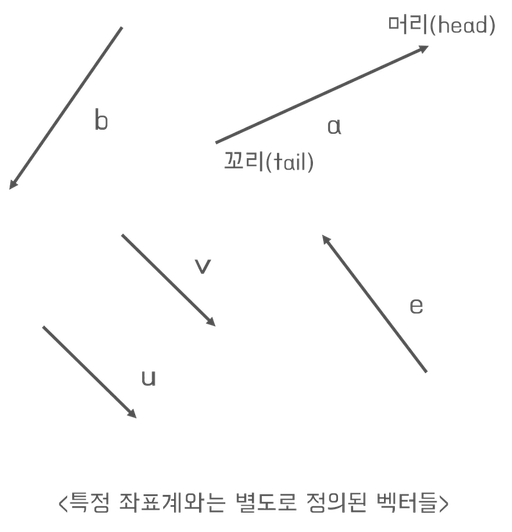
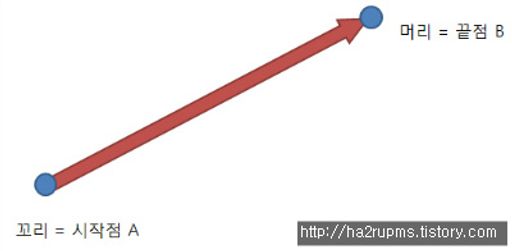
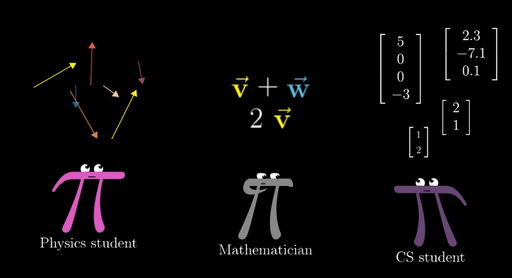벡터와 스칼라의 연산
1) 스칼라(Scalar)란?
지금까지 벡터에 대해 배워 보았다.
스칼라란?
방향은 가지지 않고 크기만 가지는 성분. 즉, 단지 크기만 있는 물리량이다.
2) 벡터 x 스칼라
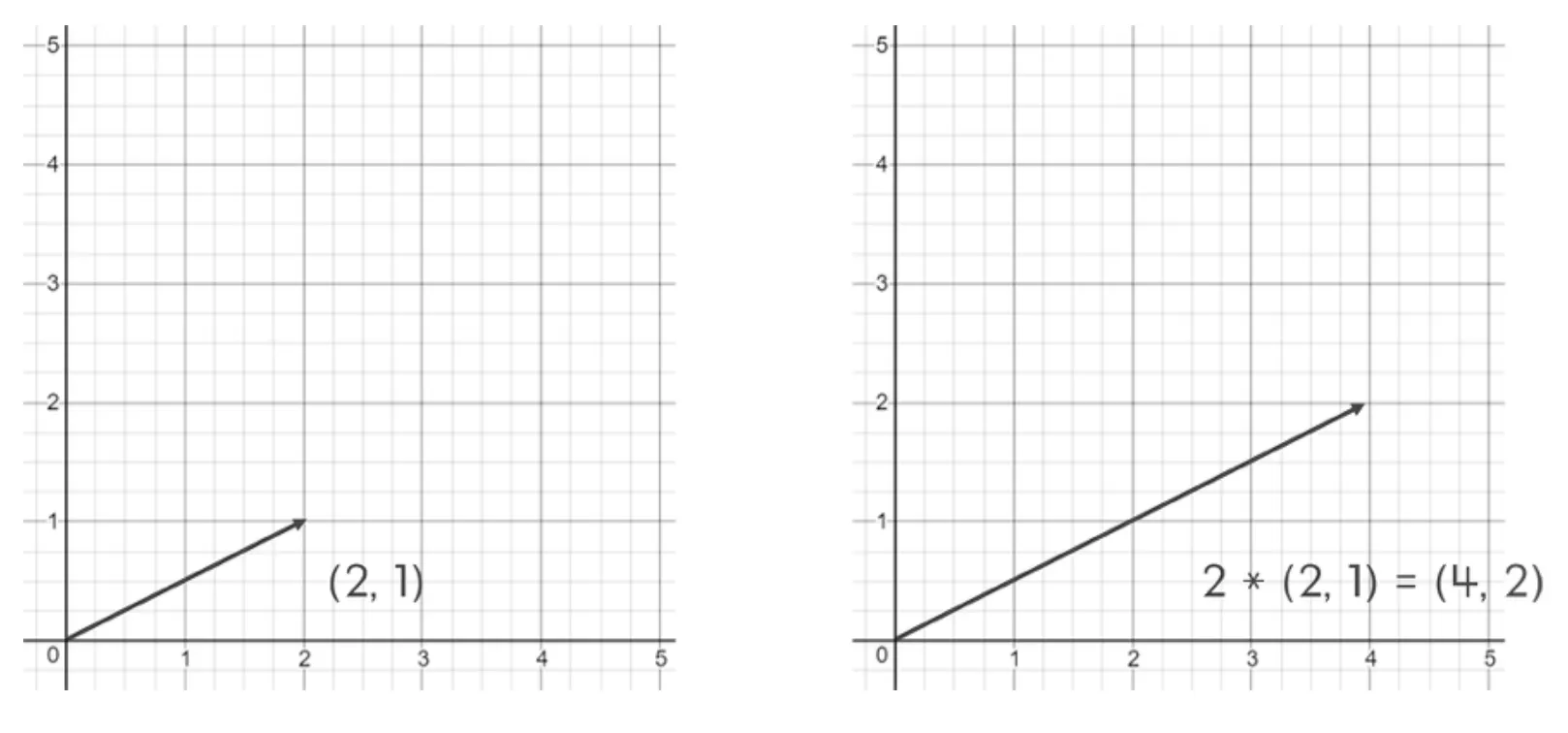
벡터와 스칼라의 곱셈 연산을 통해 벡터의 크기를 조정할 수 있다. 아래의 그림을 보자!
벡터 U = (2,1)에 2를 곱해서 (4, 2)의 벡터를 얻었다. 곱한 스칼라만큼 벡터의 크기가 변한 것을 알 수 있다.
즉, 우리는 벡터와 스칼라의 곱셈은 아래와 같이 일반화 할 수 있다.
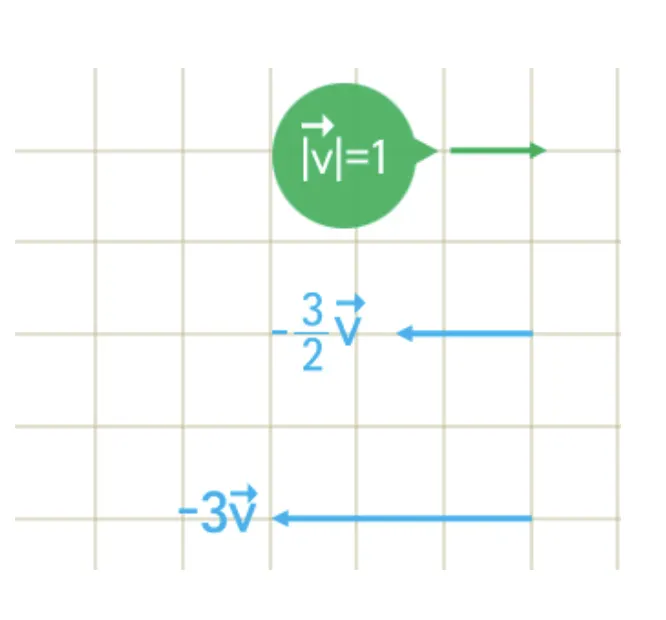
만약 스칼라의 값이 음수이면 어떻게 될까?
아래의 사진을 보면 벡터에 음수인 스칼라 값을 곱하면 방향이 반대가 되는 것을 확인할 수 있다. 즉, 벡터에서의 마이너스는 벡터의 방향을 나타내는 것이다.
3) 어디서 사용할까?
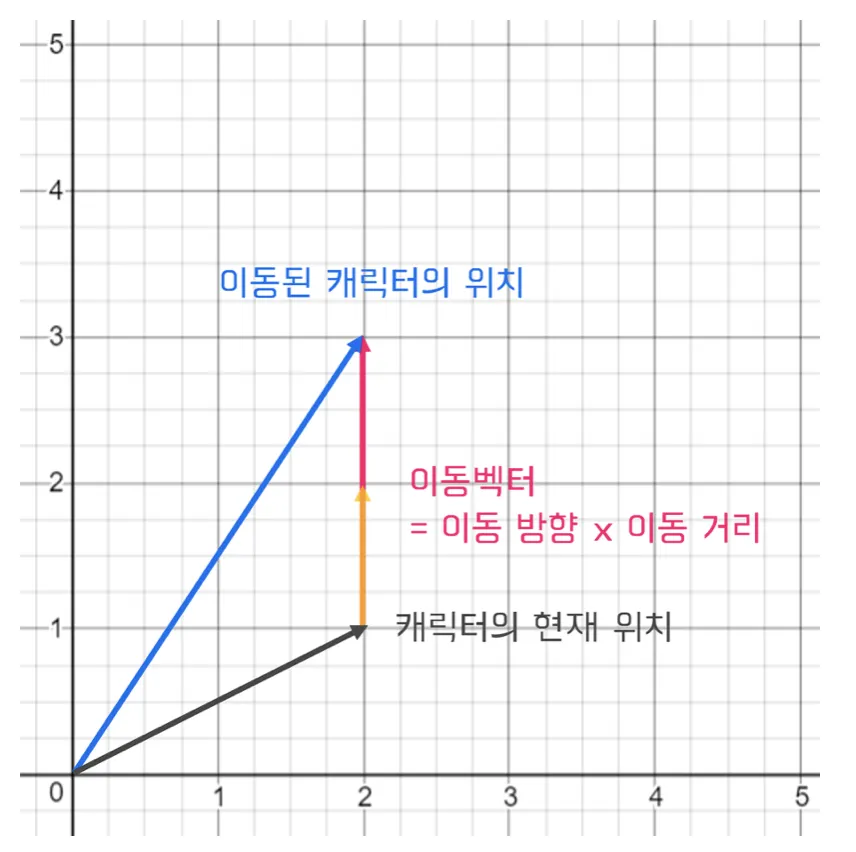
우리는 이런 연산을 프로그램에서 어떻게 사용할 수 있을까? 만약 게임이라고 생각해보자. 캐릭터의 위치 벡터 A가 있고 이동방향 B와 이동거리(스칼라) t가 있다면 최종적으로 캐릭터가 이동할 위치P 를 구할 수 있다.
벡터와 벡터의 연산
벡터와 벡터도 많은 연산이 가능하다. 덧셈과 뺄셈은 물론 내적, 외적 등 다양한 연산들이 존재한다. 가장 많이 쓰이고 벡터 연산의 기반이 되는 덧셈과 뺄셈에 대해 알아보자!
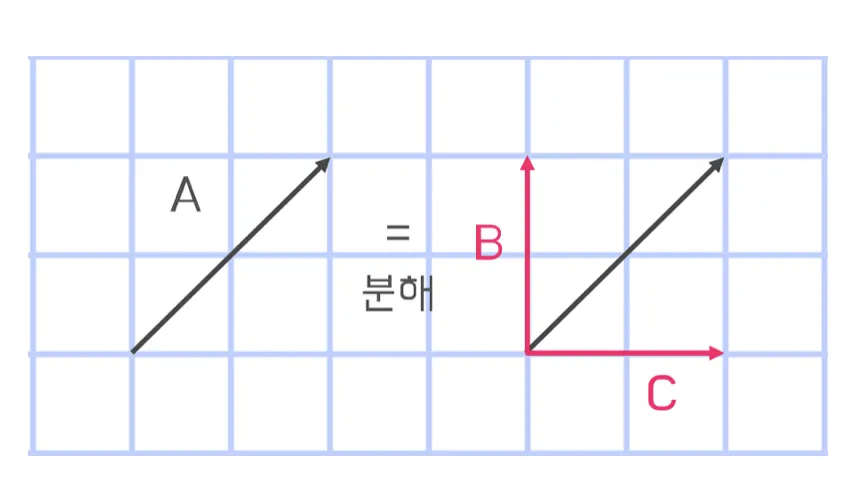
1) 벡터의 분해
우선 벡터의 연산에 대해 이해하기 전 벡터의 분해부터 공부해보자!
우리가 위의 벡터 A를 분해한 두 벡터로 표현할 수 있는 이유는 바로 분해한 성분들을 활용해서 A벡터의 크기와 방향, 시작지점을 모두 구할 수 있기 때문이다.
•
A의 크기는 피타고라스 법칙으로 간단하게 구할 수 있다.
•
A의 방향은 벡터 B, C를 변으로하는 평행 사변형을 그었을때, 벡터의 꼬리가 모여있던 부분과 새로 만들어진 평행사변형의 꼭지점을 이은 방향이다.
•
시작점은 당연히 분해한 두 벡터의 꼬리부분이다.
따라서 우리는 A라는 벡터를 간단하게 축위의 벡터를 활용해 표현할 수 있다.
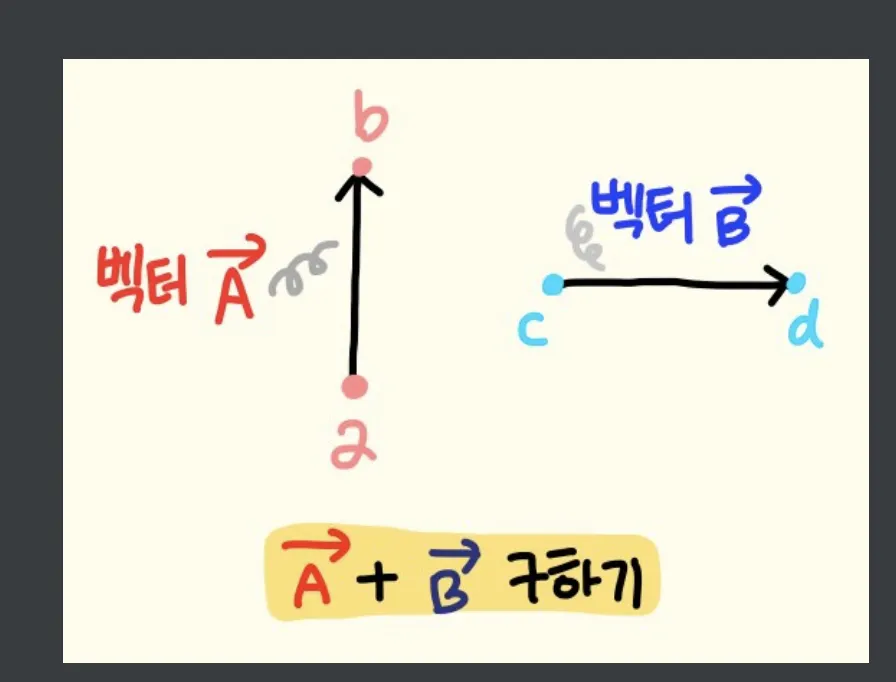
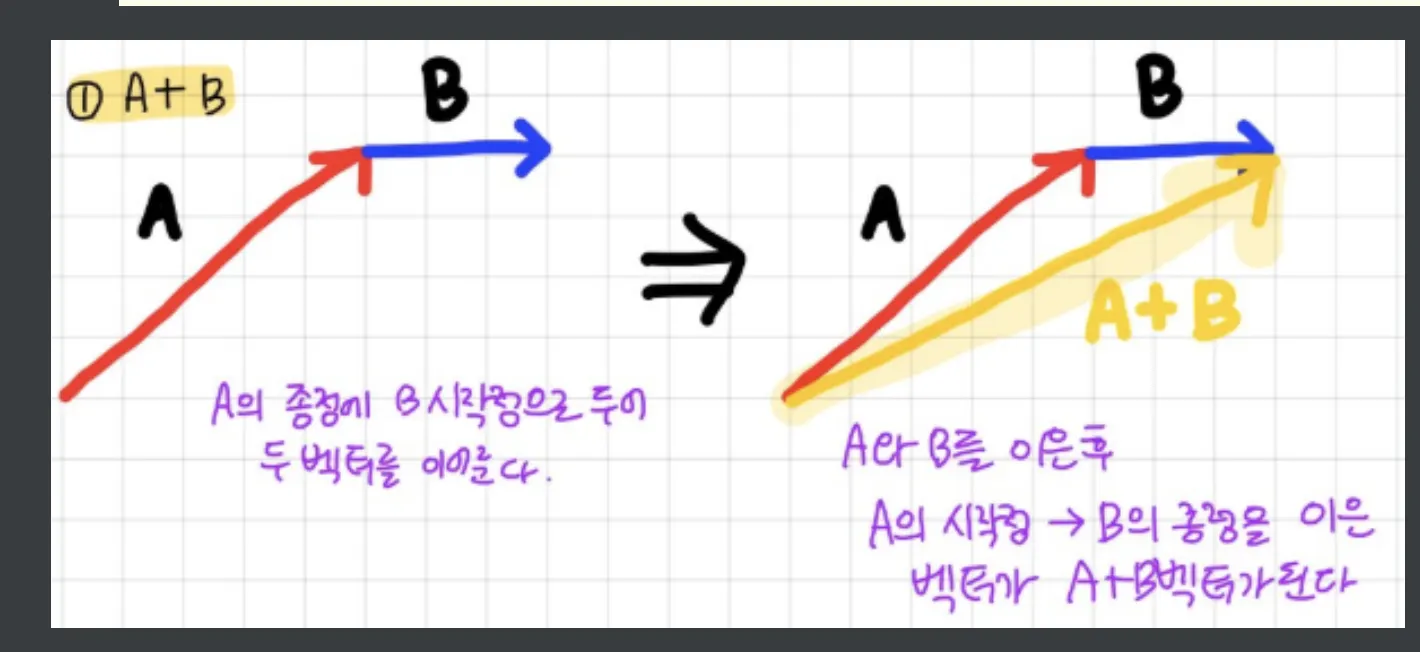
2) 벡터의 덧셈
벡터의 덧셈은 그림으로 보면 엄청 간단하다.
어디서 사용할까?
•
좌표를 이동시킬 때 많이 사용된다!
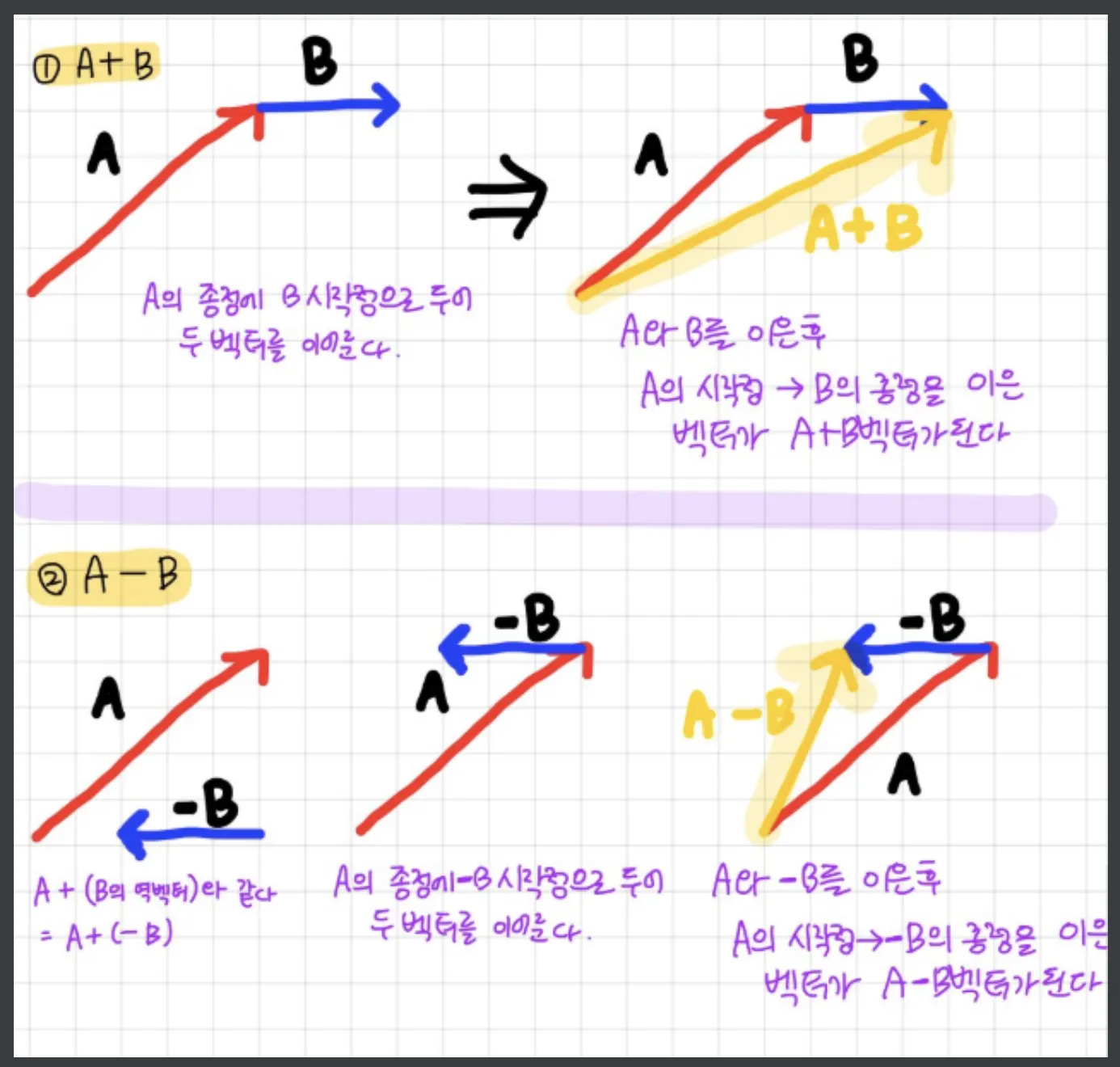
3) 벡터의 뺄셈
A벡터 - B벡터는 A벡터 + (-B)벡터와 같다! -B벡터는 이전에 공부한 역벡터 이다.
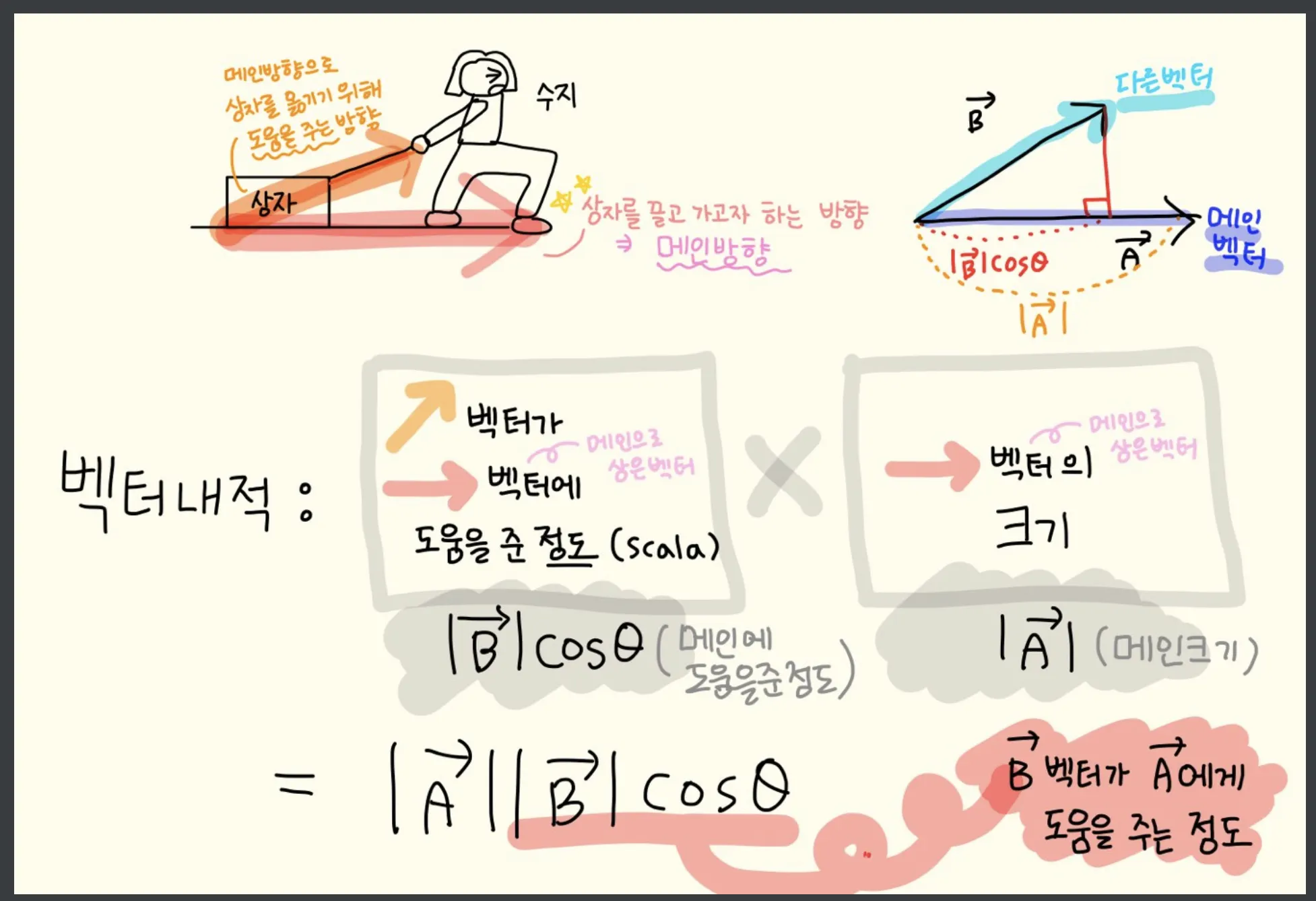
4) 벡터의 내적(dot product)
벡터의 내적은 두 벡터의 곱하기 정의 중 하나로 (다른 하나로는 외적 이 있다) 벡터를 마치 수처럼 곱하는 개념이다. 따라서 결과 값도 스칼라 값이다.
프로그래밍에서는 두 벡터의 내적을 어떻게 계산할까?
대체로 프로그래밍에서는 벡터의 성분을 (x, y)로 가지고 있다. 따라서 두 벡터의 내적을 구하는 식은 아래와 같다.
벡터의 내적은 아래와 같이 . 을 이용해서 표현한다!
내적을 구하는 이유?
그렇다면 우리는 왜 내적을 구해야 할까?
우리는 내적을 활용해서 두 벡터 사이각의 cos값을 구할 수 있다. 그래픽스의 관점에서 본다면 두 벡터 사이의 각은 매우 중요하다!
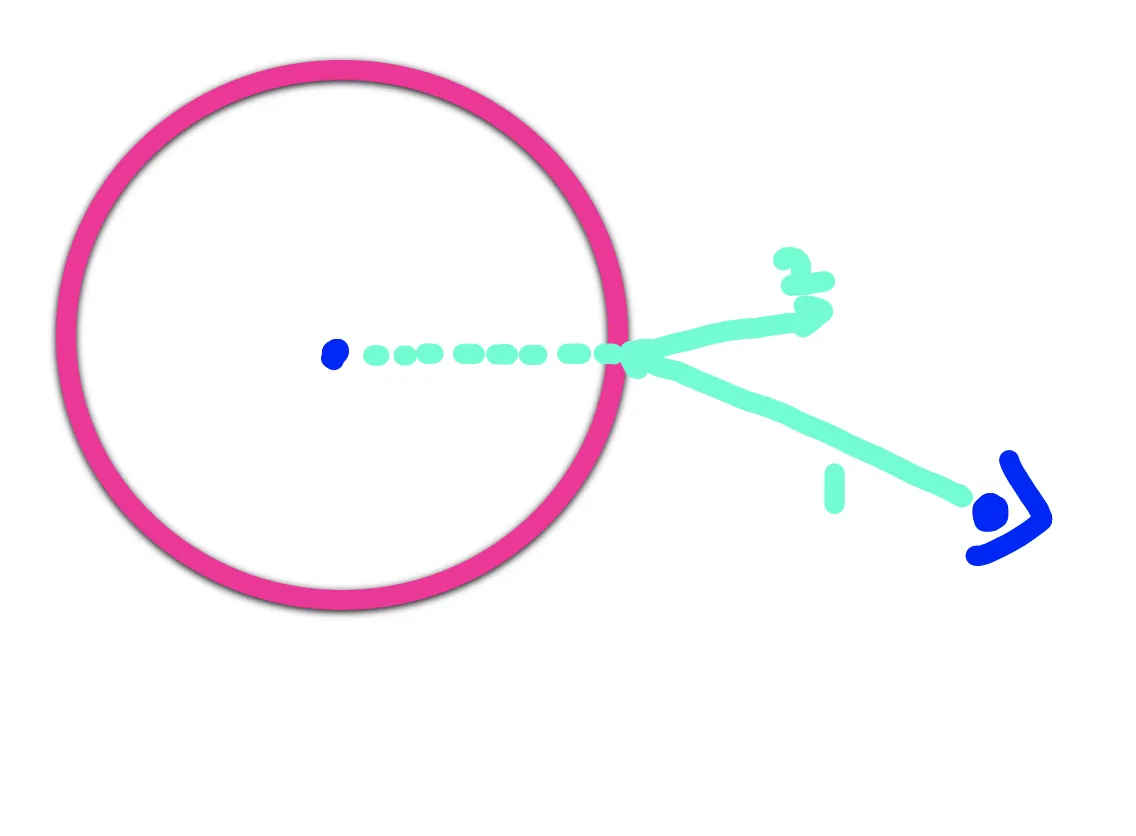
minirt의 관점에서 보자! 아래 그림을 보면 우리가 구의 한 점을 바라본다고 생각하자! 그럼 우리는 해당 지점의 법선벡터에 해당하는 (2) 번 벡터와 우리 눈에서 나가서 한 점까지 향하는 (1)번 벡터를 찾을 수 있다.
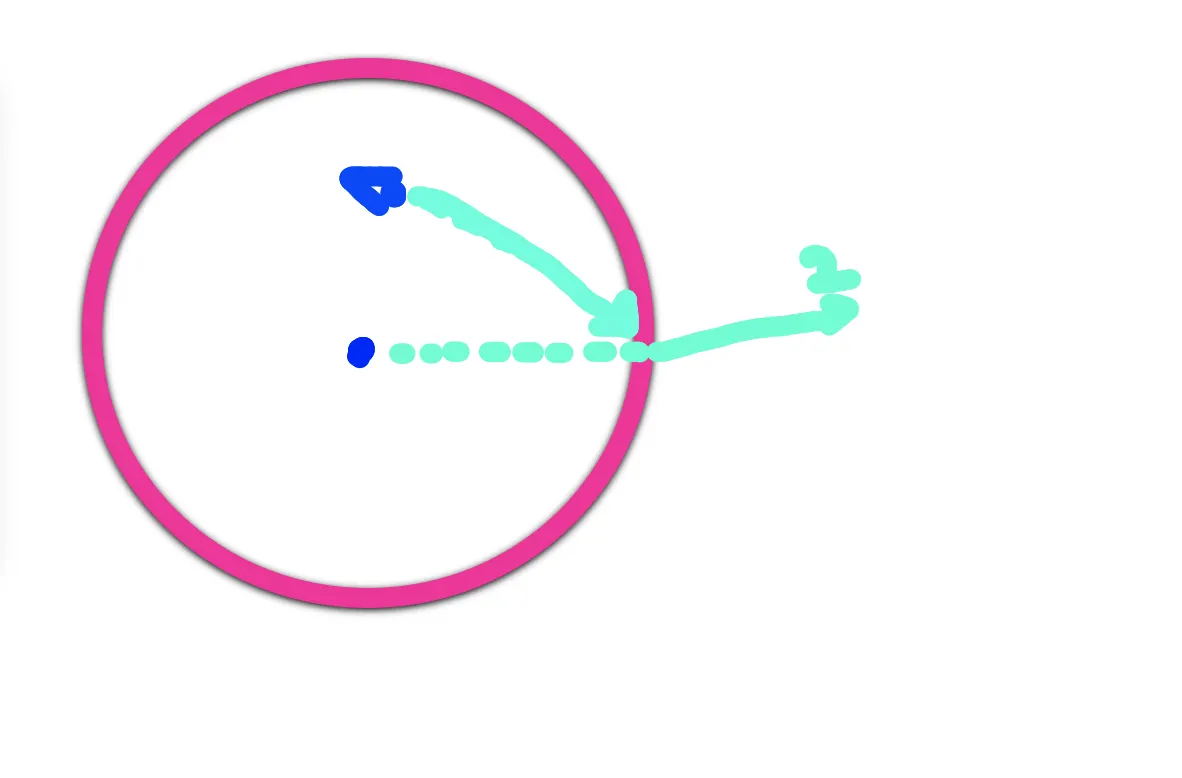
우리는 이 두 벡터의 내적을 활용해서 두 벡터 사이의 cos값을 알 수 있다! 이때 두 각 벡터가 이루는 각의 크기가 둔각이라면 우리는 구를 밖에서 보는 것이라고 생각할 수 있다. 아래의 경우는 반대의 경우이다!
두벡터가 이루는 각은 두 벡터의 꼬리를 합쳤을 때 생성되는 내각이다!
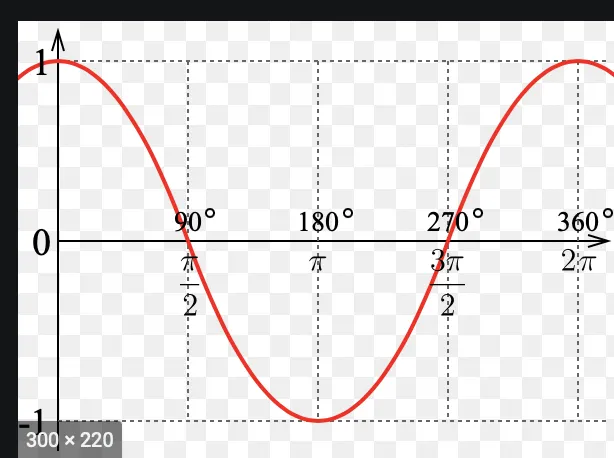
아래 코사인 그래프를 보면 예각이면 cos값이 양수, 둔각이면 cos 값이 음수인 것을 알 수 있다!
즉, 두 벡터의 내적의 결과가 양수이면 두 벡터가 이루는 각이 예각, 음수이면 둔각인 것을 알 수 있다.
5) 벡터의 외적
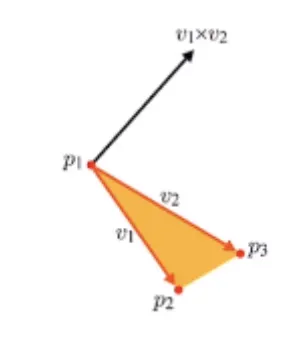
두 벡터의 외적의 결과는 두 벡터에 모두 수직인 벡터이다! 즉 아래의 그림과 같다.
벡터의 내적은 일반 곱셈 연산인 x 를 이용하여 표현한다!
외적을 구하는 이유?
외적을 구하는 이유는 간단하다! 바로 법선벡터를 구하기 위해서이다!
이제 우리는
5) 단위벡터를 활용한 벡터의 표현
프로그래밍에서는 단위벡터를 활용해서 방향벡터를 표현 하는 경우가 많다
즉 dir 벡터를 표현할 때, 단위벡터를 사용하는 것이다!
벡터의 연산에 대해 조금 더 자세히 알고싶다면 아래 페이지를 방문해보자!
