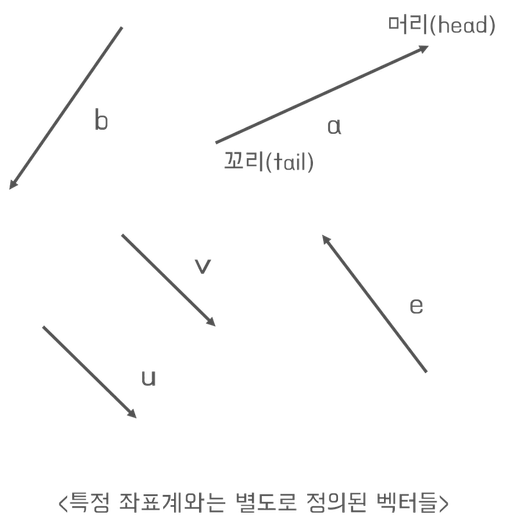
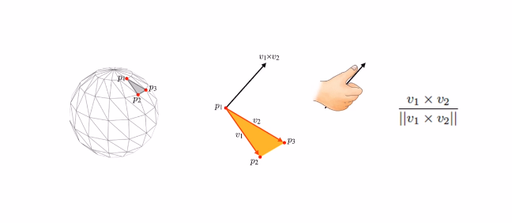
벡터 이해하기
Raytracing one weekend 문서를 보다보면 반복문을 활용해 ppm이미지를 만들고 vector클래스를 만들더니 갑자기 벡터를 활용한 코드를 만든다. 심지어 문서에 나오는 코드는 C++로 작성되어있다! 우리는 이것을 C로 바꾸어야 한다.
벡터에 대한 개념이 없으면 이전에 나왔던 클래스들도 이해하기 어렵고 해당 멤버함수들을 대체 왜 만들어야 하는지 어렵지만 차근차근 하나씩 배워가면 이후 연산들도 어렵지 않다!
벡터란?
minirt과제를 진행하려면 벡터에 대해 이해하고 넘어가는 것이 필수이다. 우선 코드를 잡기 전에, 벡터에 대해 알아보자!
벡터란?
크기와 방향을 함께 가지는 성분
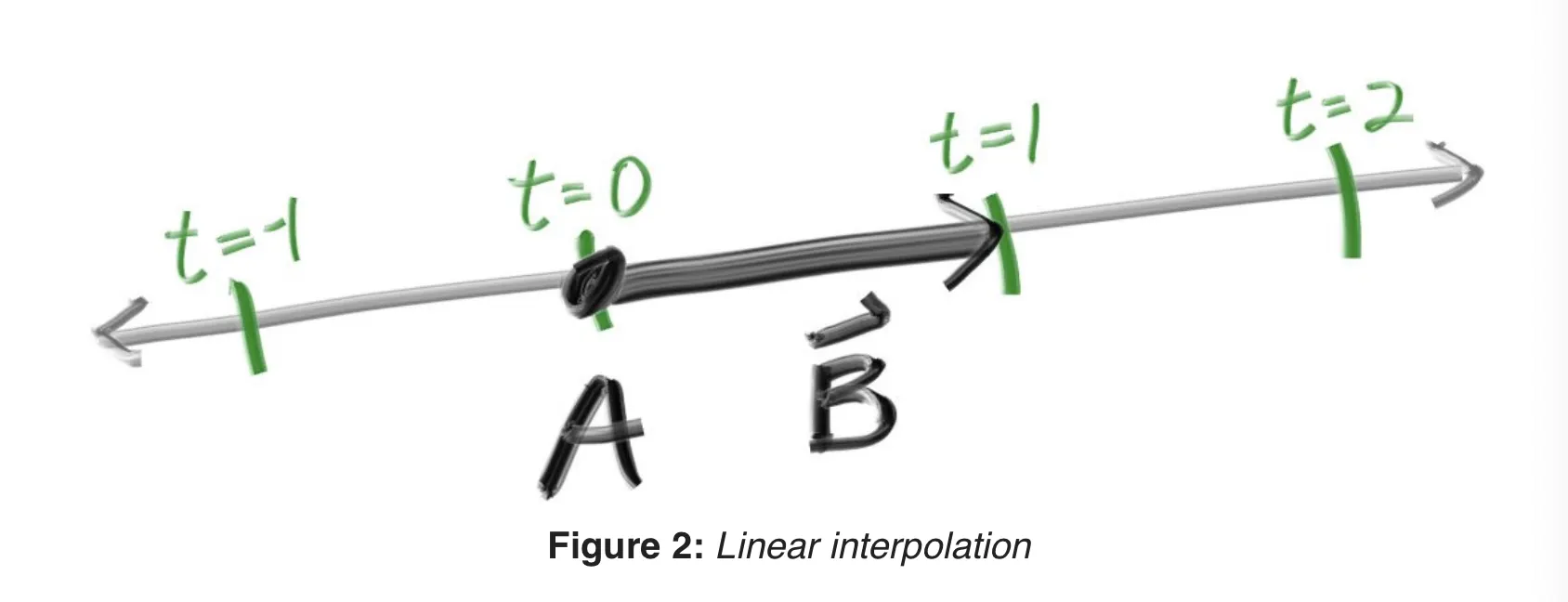
선형대수에서 벡터에 대해 이야기 할때, 원점에 꼬리를 둔 화살표를 하나 생각하는 것이 좋다. 아래의 그림을 살펴보자.
1차원 좌표계인 위의 그림을 보면 t = 0 인 좌표에서 t = 1인 좌표를 가리키는 크기가 1인 벡터가 있다. 우리는 여기서 벡터를 시작지점 + 크기 * 방향로 표현할 수 있다.
즉 이 그림의 벡터 = A + 1 * b 인 것이다. 이 식을 일반화 하게 되면 아래와 같다.
벡터의 표현
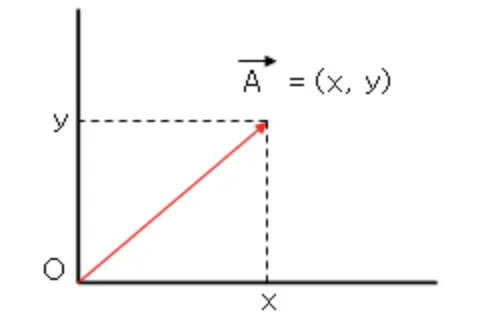
하지만 우리가 사용할 좌표계에서는 크기와 방향(즉, t와 b)를 바로 알기 어렵다. 우리는 좌표계를 활용해 벡터의 성분을 분해한 표기법을 사용할 것이다. 예를들면 아래의 벡터 A는 A(x, y) 로 표기할 수 있다.
혹은 아래 사진처럼 변수 위에 → 를 달아서 표현하기도 한다.
기하학적으로 벡터의 크기는 방향을 가진 선분의 길이이다. 벡터의 성분이 주어졌다고 할 때, 우리는 피타고라스 정리를 활용해 벡터의 크기를 알 수 있다! (|A| 는 벡터 A의 크기를 나타낸다)
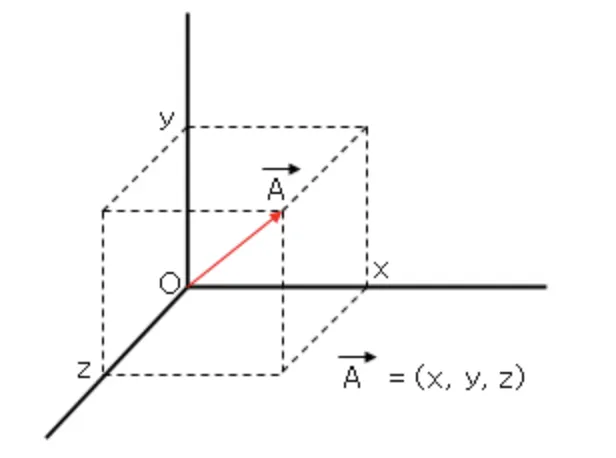
minirt과제를 진행한다면 3차원 벡터를 표현해야한다. 3차원 벡터도 위의 방식을 사용하면 어렵지 않게 표현할 수 있다!
같은 벡터
•
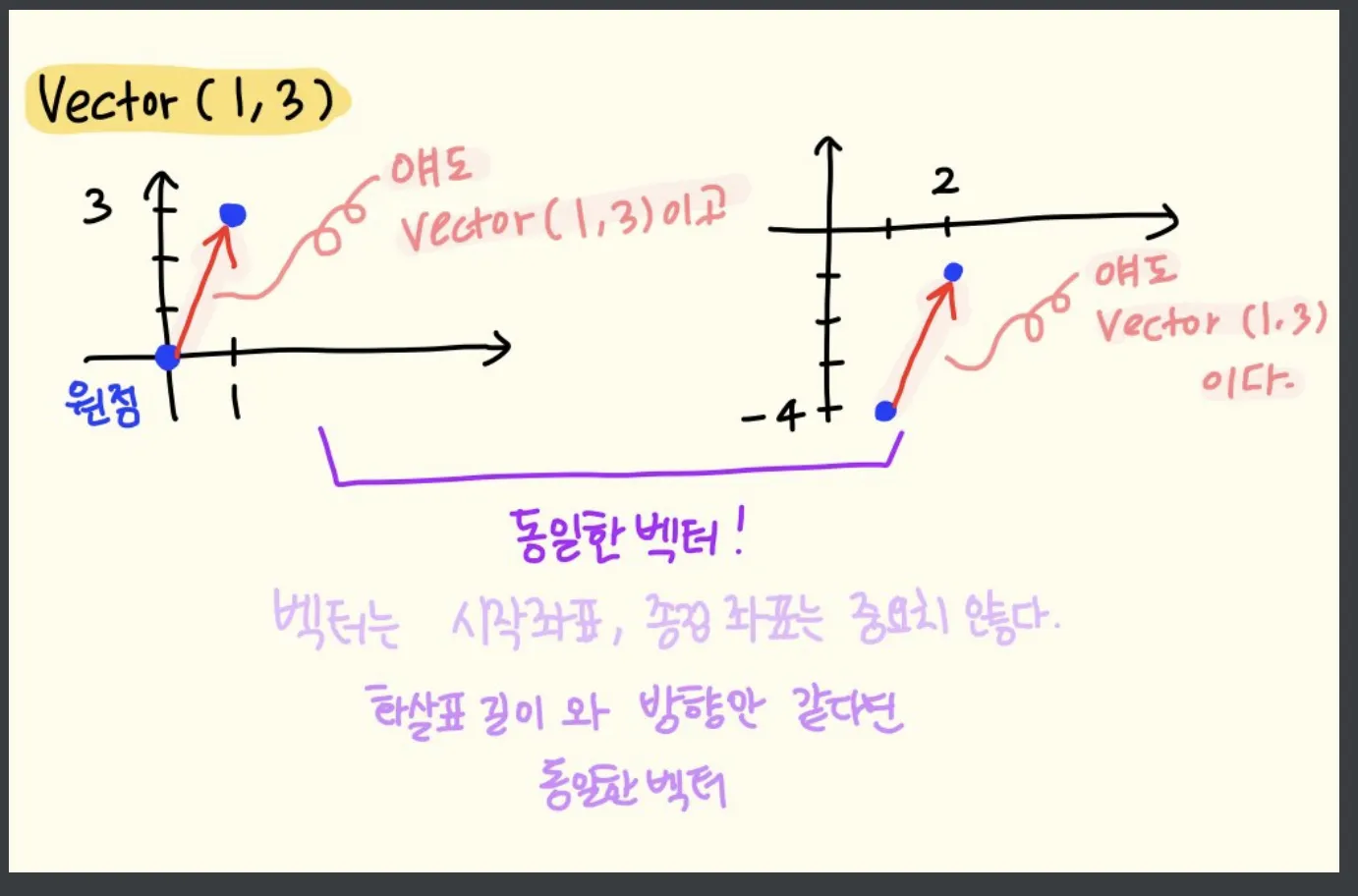
시작점, 종점과 상관 없이 벡터의 길이와 방향이 모두 같으면 같은 벡터이다!
•
벡터에게 위치는 중요하지 않다!
프로그래밍에서의 벡터
•
벡터는 <기하학>에서의 개념이지만 <대수학>영역인 프로그래밍에서 어떻게 쓰이는지를 잘 파악해야 한다.
•
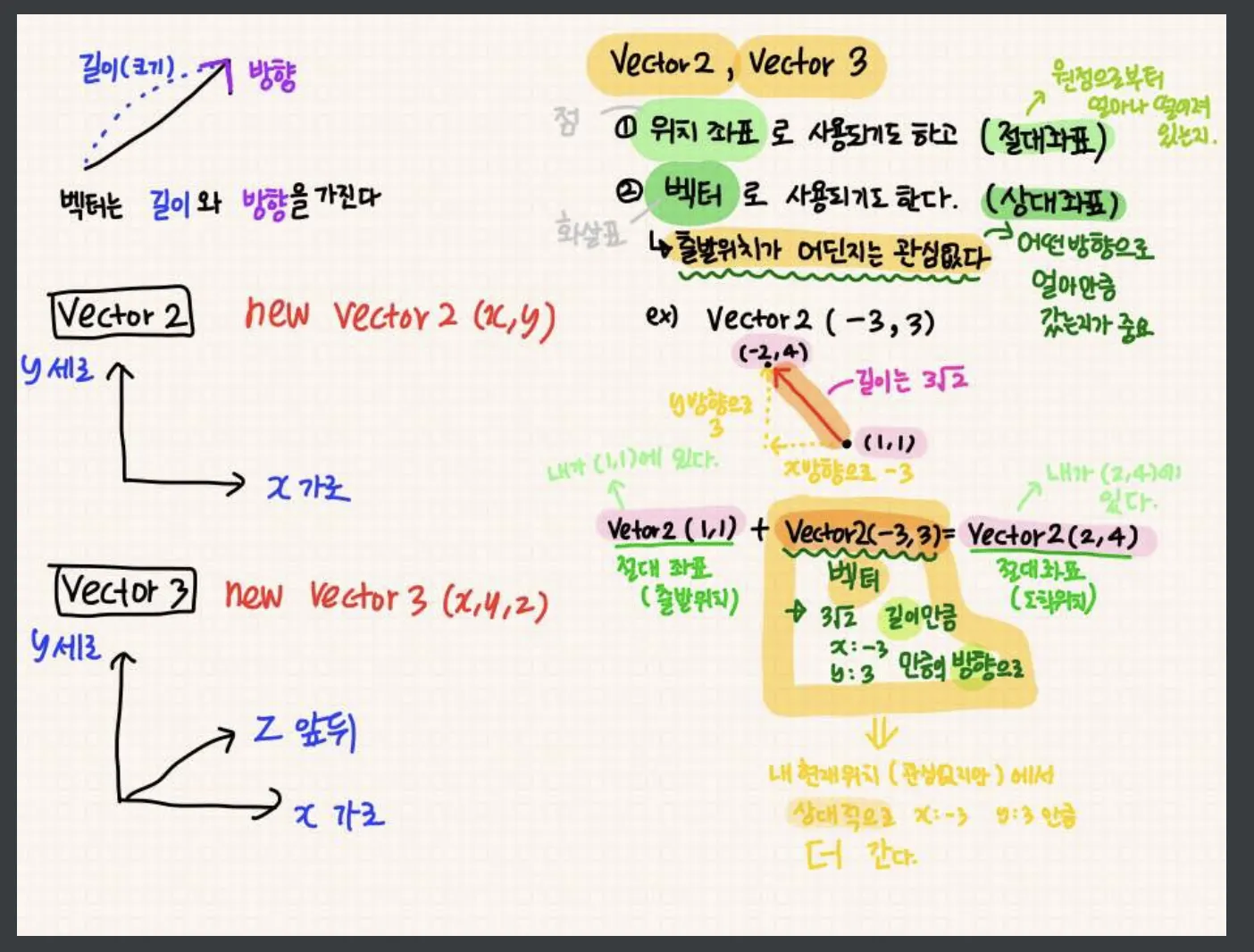
Vector2(x, y), Vector3(x, y, z) 으로 나타낼 수 있다.
•
x, y, z 는 각각 벡터의 성분이 된다.
1.
위치 좌표로 쓰임 (절대좌표)
•
사실 위치 좌표는 스칼라로 보이더라도 이 또한 원점을 시작점으로, 해당 위치를 종점으로 하여 화살표로 이어진 벡터라고 해석할 수 있다.
•
위치 좌표로서의 Vector2(2, 4)는 Vector2(0, 0) 원점을 시작점으로 했을 때 Vector2(2, 4)로 향하는 벡터라고도 할 수 있다.
2.
벡터로 쓰임 (상대좌표)
•
어떤 방향으로 얼마만큼의 크기 만큼 변화했는지의 정도
영벡터 (Zero Vector)
영벡터는 모든 성분이 0인 벡터를 말한다! 즉 좌표계의 원점이다. 굵은 0으로 표현하기도 한다.
•
영벡터는 방향이 없다!
•
0 = (0, 0, 0)
역벡터 (Inverse Vector)
크기는 같고 방향만 정반대인 벡터! 특정 벡터의 시작점과 종점이 바뀐 것을 의미한다.
•
A 벡터의 역벡터는 -A벡터이다!
•
A + (-A) = 0
단위벡터 (Unit Vector) = 방향 벡터
단위벡터는 크기가 1인 벡터이다.
단위 벡터는 크기는 1이지만 방향을 가지고 있으므로, 여기에 값을 곱해주면 방향은 같지만 크기가 다른 벡터를 마음대로 만들 수 있다. 혹은 크기는 무시하고 방향만 나타내기 위해서 사용한다.
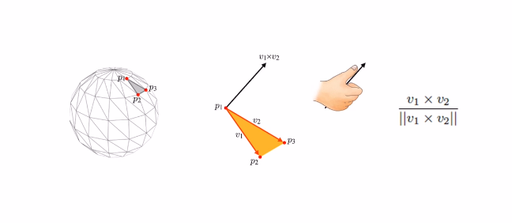
모든 벡터는 정규화(normalize) 과정을 거쳐 단위 벡터로 만들 수 있다. 벡터 U를 (x, y)라고 했을 때, 정규화를 하는 식은 아래와 같다.
위 식은 벡터의 각 성분에 벡터의 크기를 나눠준 것이다!
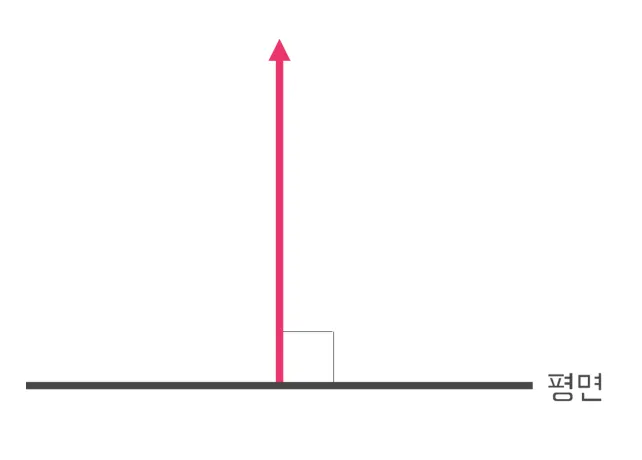
법선벡터 (Normal Vector)
법선벡터는 어떤 표면(평면)에 수직인 뱡항으로 뻗어나가는 벡터이다.
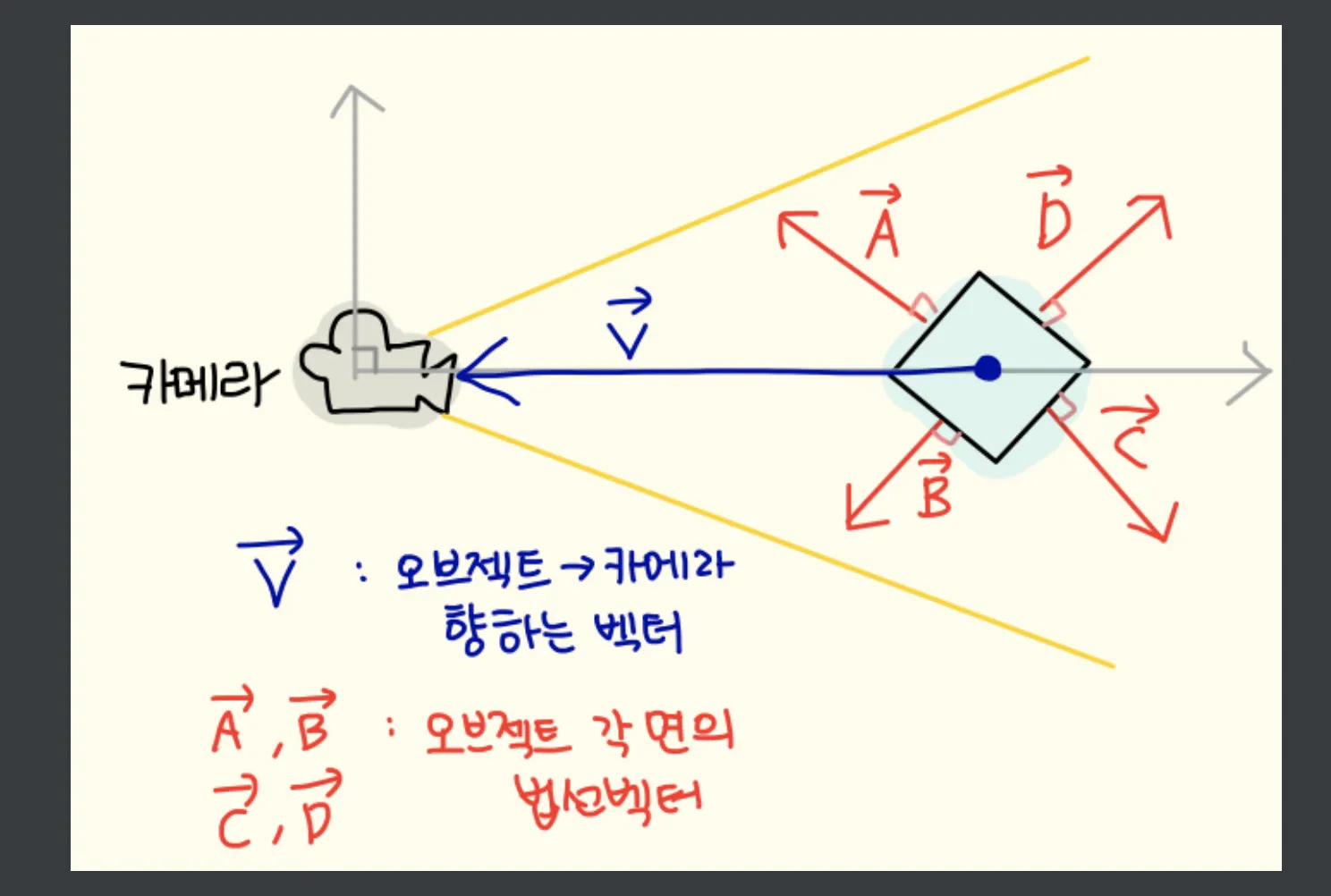
컴퓨터 그래픽스에서는 모든 Normal Vector(법선벡터)를 Unit Vector(단위벡터)로 표현한다. 따라서 아래의 식을 활용해 구할 수 있다. (단위벡터로 표현하기 위해서는 벡터의 크기만큼 나눠주어야 한다.)법선벡터는 왜 필요한 걸까?
법선 벡터를 사용함으로써 울퉁불퉁한 곡면을 부드럽게 표현, 완벽한 조명 적용 가능 하다고 한다. 또한 우리가 카메라로 특정 물체를 보고싶을 때, 물체의 한 면이 카메라의 시야에 들어오는지 법선벡터를 활용해 알 수 있다!
법선 벡터를 사용하는 예제를 조금 더 보고싶다면 아래 페이지를 참고해보자!
그래픽스 모델링에서 사용하는 법선 벡터에 대해 궁금하다면 아래 페이지를 참고해보자!
