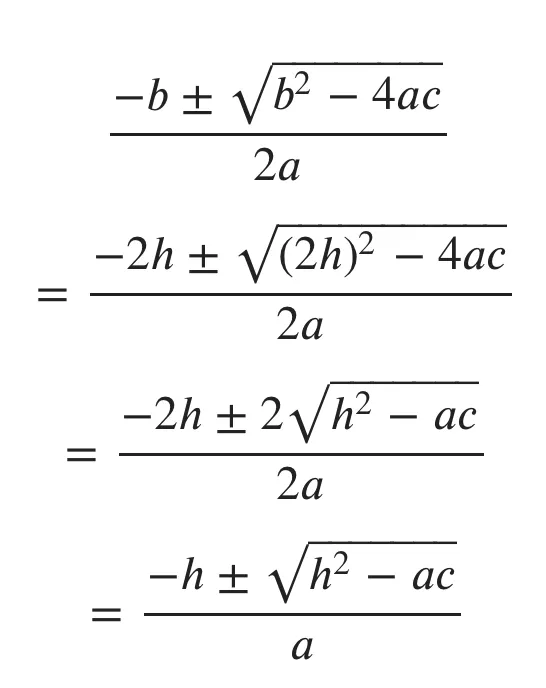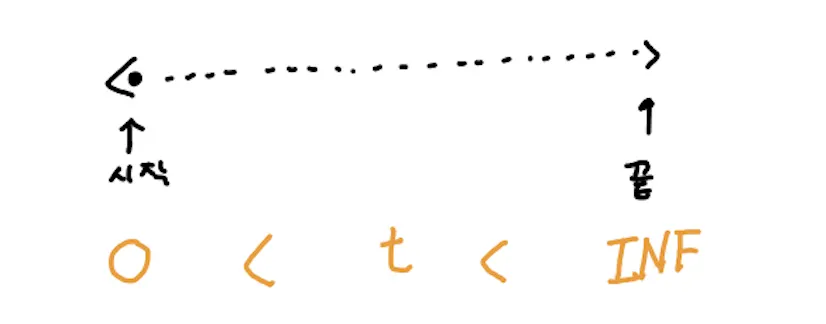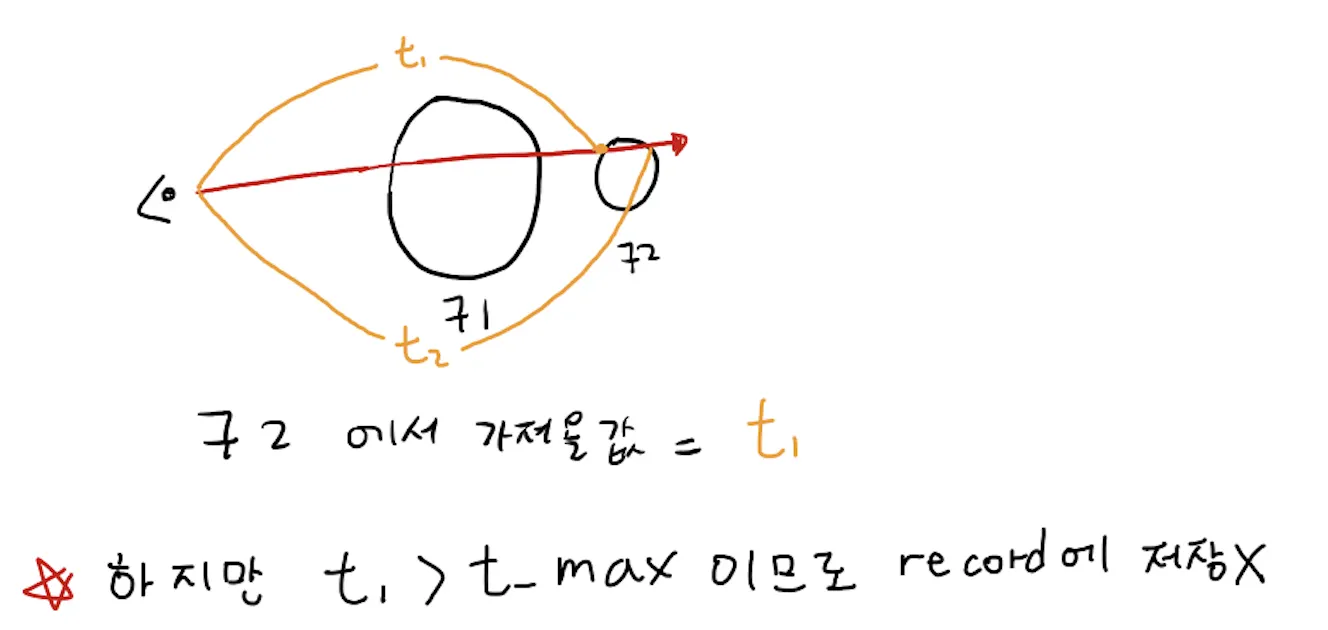// 책에서의 6장 내용
Raytracing One Weekend 식 이해하기! 4
이번 시간에는 꽤나 알아야 할 식들이 많다 
하지만 차근차근 하나씩 한다면 해낼 수 있다!!!!
법선벡터(Nomal vector)에 대해 이해하고 있고 내적의 결과에 대한 이해가 잘 되어있다면 어렵지 않게 앞부분을 넘어갈 수 있을 것이다!
Surface Normals and Multiple Objects
1) Shading with Surface Normals
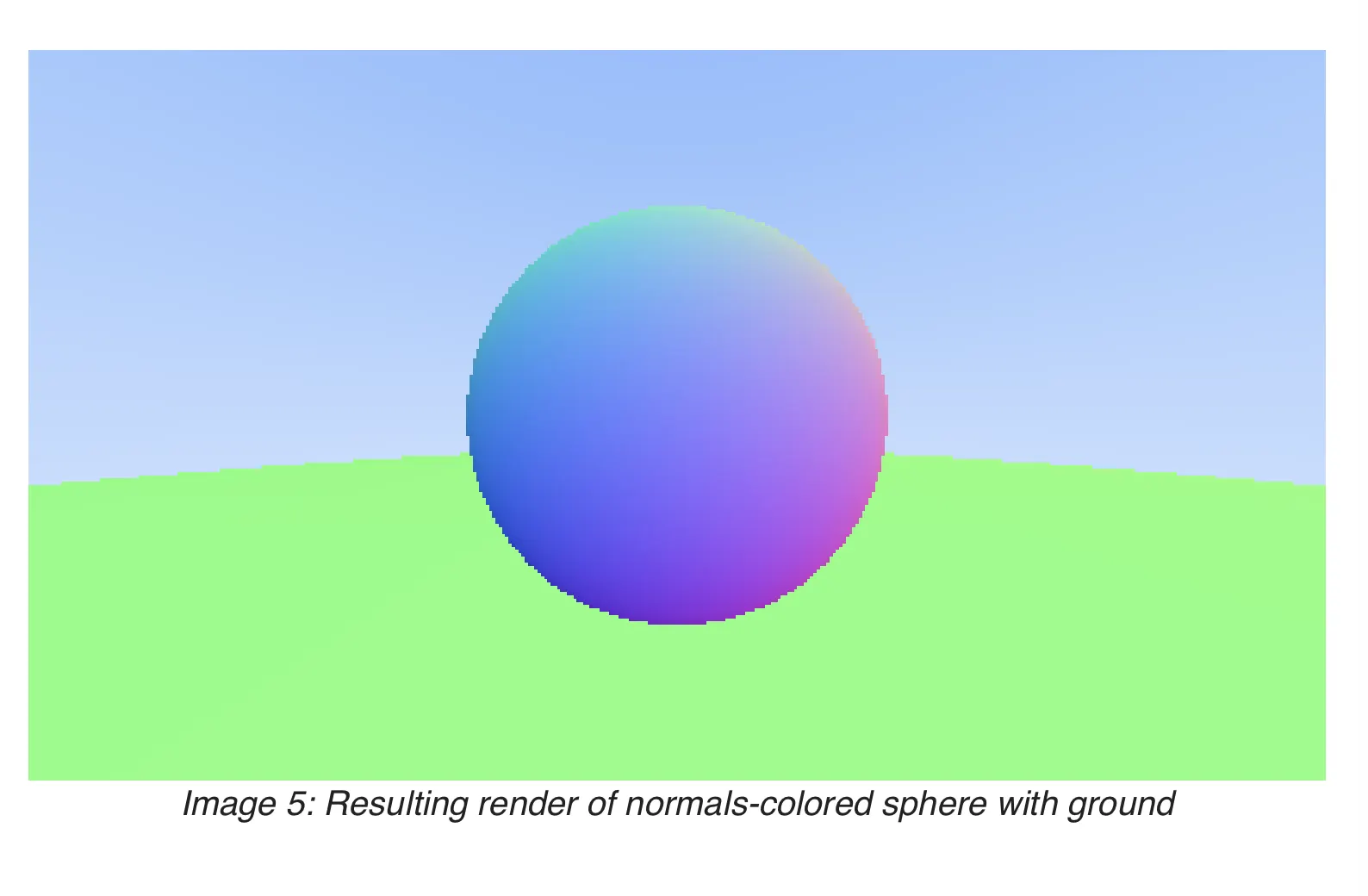
표면에 따라서 색을 좀더 입체적으로 입혀보자! 우리는 ray를 쏴서 구와 부딪힌 P지점에서의 법선 벡터를 구한뒤, 해당 법선 벡터의 성분을 활용해 구에 조금 더 다양한 색을 입혀볼 것이다!
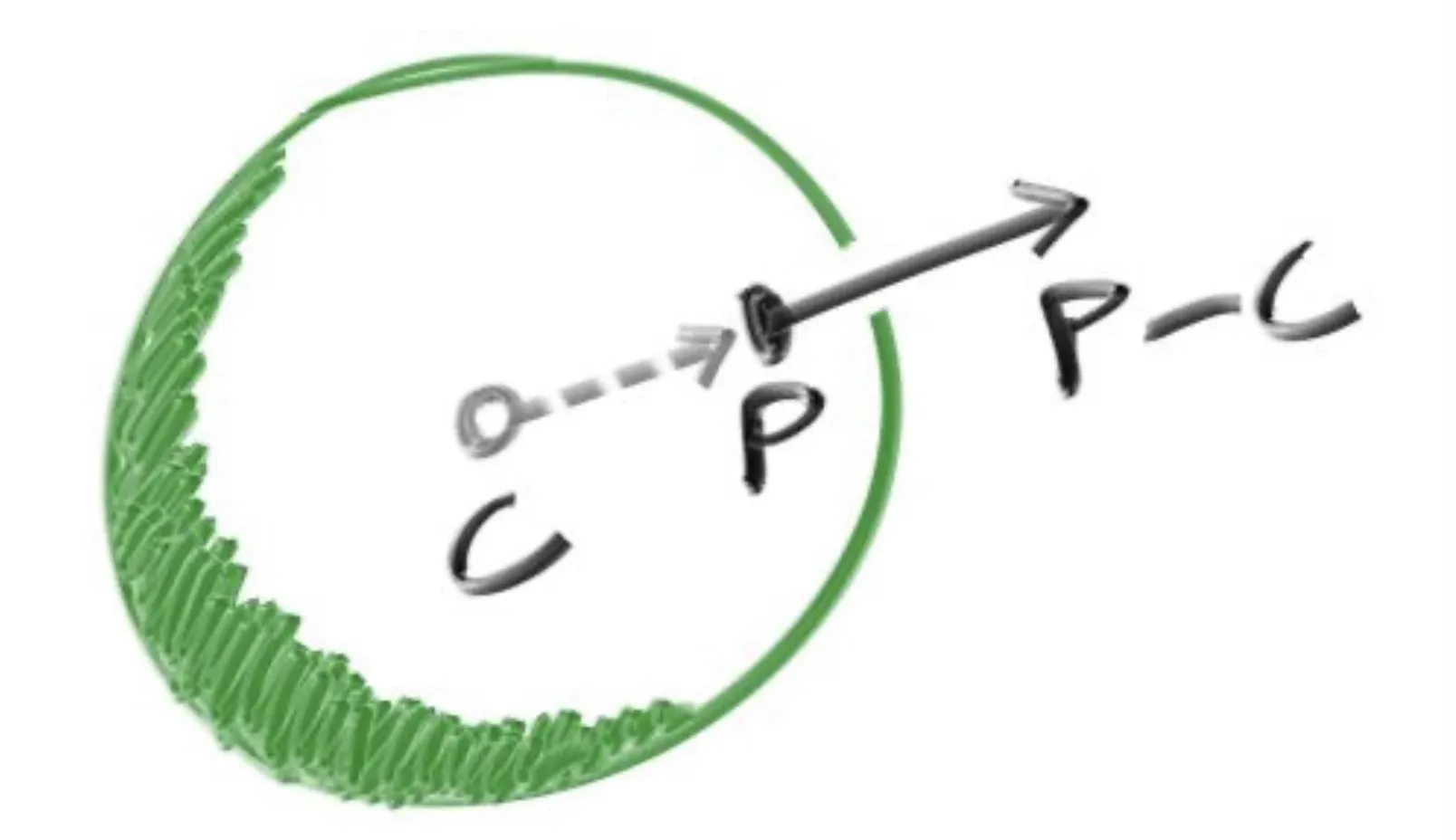
정점 P에서의 법선벡터를 구하기 위해 정점 P에서 정점 C를 빼줄것이다.
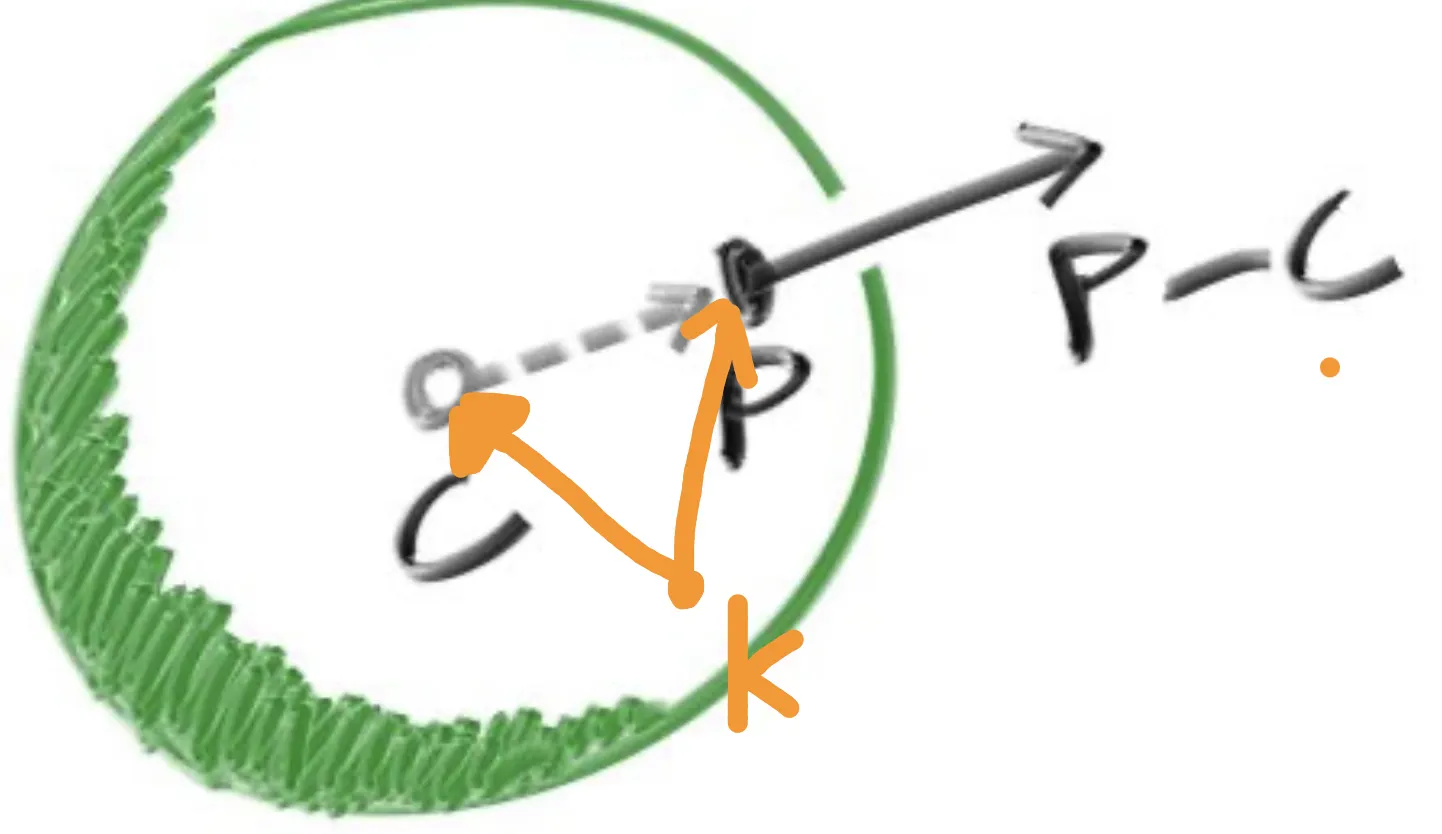
만약, 정점좌표 연산이 어렵다면 임의의 점 K를 잡고 KP 벡터와 KC벡터가 있다고 생각해보자
벡터의 뺄셈은 이전에 배웠기 때문에 쉽게 구할 수 있다! KP - KC 벡터를 생각해보면 구 중심에서 P를 지나 바깥을 향하는 벡터를 구할 수 있다.
즉 P - C 는 구 위의 정점 P에서의 법선벡터임을 알 수 있다.
우리는 정점좌표를 구하기 위해 이전 챕터에서 배운 t의 해를 구해야 한다. 즉, 근의 공식으로 나온 결과를 return해 줄 것이다! 책의 식을 바로 C로 바꾸어서 가져와 보았다.
// C code
double hit_sphere(t_vec center, double radius, t_ray r)
{
double a;
double b;
double c;
double discriminant;
vec3 oc = vec(r.origin.x - center.x // 근의 공식을 사용해 해를 구하는 과정
,r.origin.y - center.y
,r.origin.z - center.z);
a = vec_dot(r.dir, r.dir);
b = 2.0 * vec_dot(oc, r.dir);
c = vec_dot(oc, oc) - radius * radius;
discriminant = b * b - 4 * a * c;
if (discriminant < 0)
return (-1);
else
return ((-b - sqrt(discriminant)) / (2.0 * a));
}
C
복사
ray_color코드도 크게 바뀐것이 없다. 수정된 부분은 구의 색을 칠할때 계산한 법선 벡터의 단위벡터를 구해서 각 성분에 따라 색이 바뀌는 코드로 수정되었다.
// C code
t_vec ray_color(t_vec r)
{
t_vec center;
t_vec color;
t_vec unit_direction;
t_vec tmp;
t_vec N;
double t;
center = vec(0, 0, -1);
t = hit_sphere(center, 0.5, r);
if (t > 0.0) // 만약 해가 있다면!
{
tmp = ray_at(t); // t를 활용해서 tmp 벡터를 구한다.
N = vec_unit(vec(tmp.x - 0, tmp.y - 0, tmp.z - (-1))); // tmp 벡터의 unit벡터를 구한다!
color = vec_mul(vec(N.x + 1, N.y + 1, N.z + 1), 0.5);
return (color);
}
// 해가 없다면~!
unit_direction = vec_unit(r.dir);
t = 0.5 * (unit_direction.y + 1.0);
color = vec(1.0 - 0.5 * t, 1.0 - 0.3 * t, 1.0);
return (color);
}
C
복사
2) Simplifying the Ray-Sphere Intersection Code
이 파트에서는 위의 수식을 조금 간단하게 바꿔볼 것이다! 책의 코드를 보면 b가 항상 2의 배수인 것을 알 수 있다!
(2 x val 이기 때문에)
그렇다면 우리는 b 를 2h 라고 생각할 수 있고 아래와 같이 근의 공식을 조금 간단하게 표현할 수 있다!
위의 수정사항을 반영한 코드이다!
// C code
int hit_sphere(t_vec center, double radius, t_ray r)
{
double a;
double half_b; // b가 half_b로 바뀌었다
double c;
double discriminant;
vec3 oc = vec(r.origin.x - center.x
,r.origin.y - center.y
,r.origin.z - center.z);
a = vec_dot(r.dir, r.dir);
half_b = vec_dot(oc, r.dir); // 여기서 곱해주는 2를 나눠준 것이다
c = vec_dot(oc, oc) - radius * radius;
discriminant = half_b * half_b - a * c; // 식도 조금 쉽게 바뀌었다
if (discriminant < 0)
return (-1);
else
return ((-b - sqrt(discriminant) / a)); // 마지막에도 a만 나눠주면 된다
}
C++
복사
3) An Abstraction for Hittable Objects
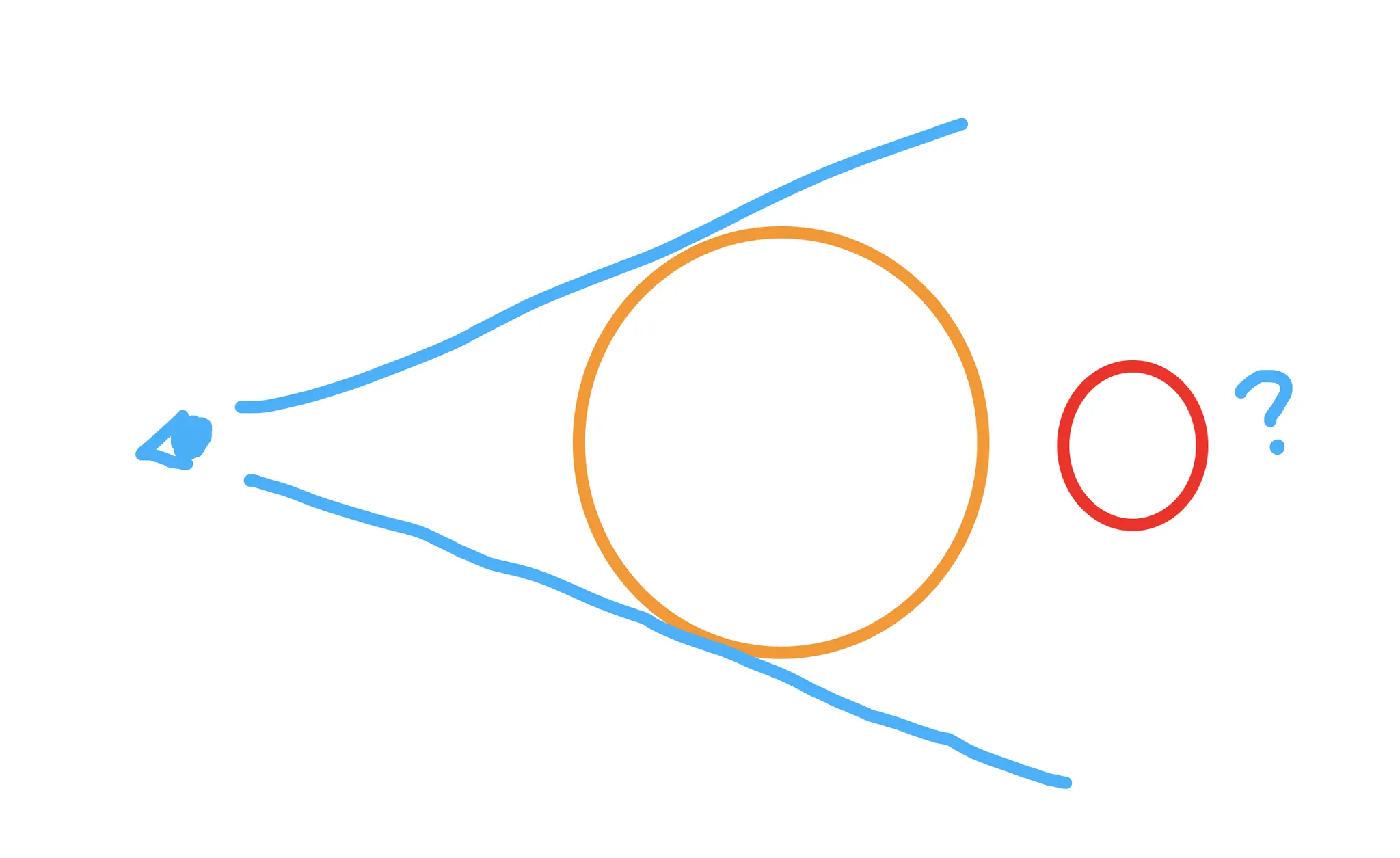
이번 챕터에서는 어떤 오브젝트들이 보여질 수 있는지 체크한다. 예를들어 화면에 구가 2개가 있는데 만약 큰 구 뒤에 작은 구가 있다면 작은 구는 화면에 보여지지 않아야 한다.
우리는 이것을 어떻게 처리할 수 있을까!
공식을 보기 전에 책에서 처리하는 방식을 살펴보자!!
1.
우선 우리가 쏠 ray의 범위를 구한다!
•
t_min = 0
•
t_max = INF
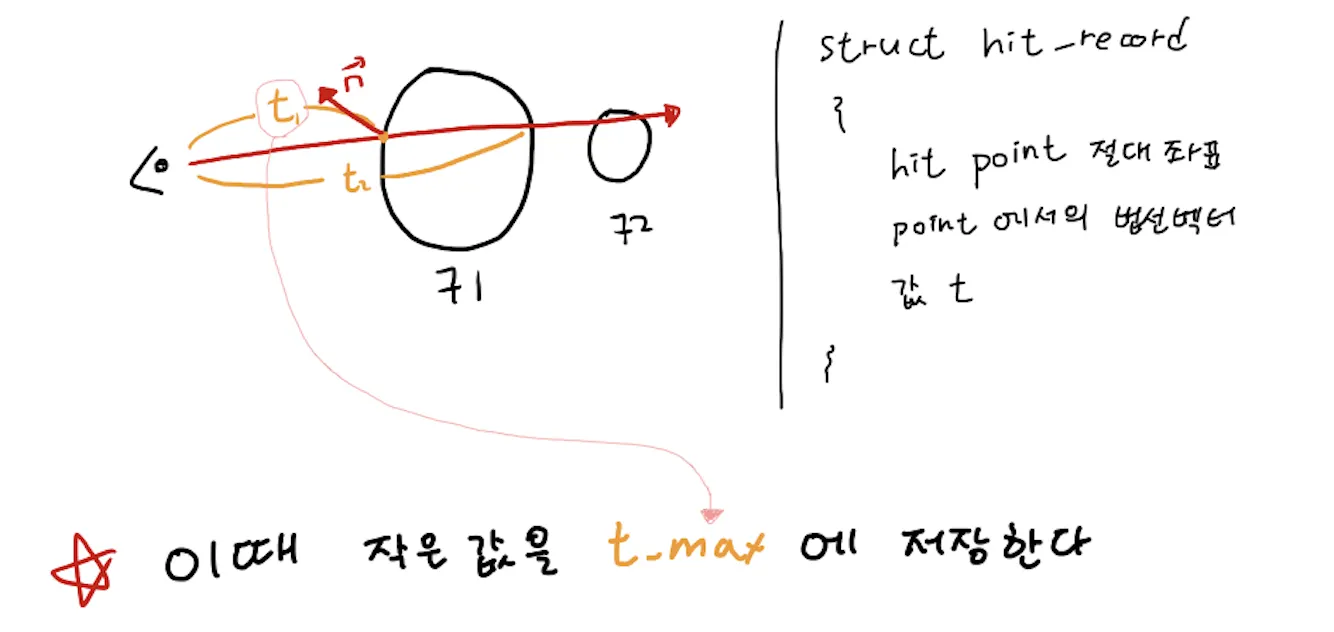
2.
첫 구에서의 값을 hit_record에 저장한다!
3.
이제 두번째 구로 ray를 쏘는데 t_max의 값이 바뀌어있다!
이렇게 hit_record 구조체를 활용해서 우리가 여러 오브젝트들을 가지고 와도 가장 먼저 보이는 물체를 알아낼 수 있는 것이다!
아래 본문의 코드는 hit_record가 저장하는 정보들을 나타내고 있다. 아래에 클래스로 함수가 선언되어 있는데 우선은 넘어가도록 하자!
#ifndef HITTABLE_H
#define HITTABLE_H
#include "ray.h"
struct hit_record {
point3 p;
vec3 normal;
double t;
};
class hittable {
public:
virtual bool hit(const ray& r, double t_min, double t_max, hit_record& rec) const = 0;
};
#endif
C++
복사
아래 코드는 구가 가지는 정보들을 나태내고 있다.
class sphere : public hittable {
public:
sphere() {}
sphere(point3 cen, double r) : center(cen), radius(r) {};
virtual bool hit(
const ray& r, double t_min, double t_max, hit_record& rec) const override;
public:
point3 center;
double radius;
};
C++
복사
대략 위 코드를 C언어로 변경한다면 아래와 같다.
typedef struct s_sphere
{
t_vec center; // 구의 정점좌표
double r; // 구의 반지름
// 함수 포인터로 구현한 hit method..
int (*hit)(struct s_world *this, t_ray *ray, double min, double max, t_hit_record *out);
} t_sphere;
C++
복사
이제 hit함수의 모습을 알아보자!!
bool sphere::hit(const ray& r, double t_min, double t_max, hit_record& rec) const {
vec3 oc = r.origin() - center;
auto a = r.direction().length_squared();
auto half_b = dot(oc, r.direction());
auto c = oc.length_squared() - radius*radius;
auto discriminant = half_b*half_b - a*c;
if (discriminant < 0) return false;
auto sqrtd = sqrt(discriminant);
...
C++
복사
사실 이부분 까지는 크게 바뀐것이 없다! 근의 공식을 활용해서 t의 값을 찾는 것이다!
이제 아래에서 추가된 부분을 살펴보자!
// Find the nearest root that lies in the acceptable range.
auto root = (-half_b - sqrtd) / a; // 1번
if (root < t_min || t_max < root) { // 2번
root = (-half_b + sqrtd) / a; // 2 - 1번
if (root < t_min || t_max < root) // 2 - 2번
return false; // 2 - 3번
}
// 3번 ...
rec.t = root;
rec.p = r.at(rec.t);
rec.normal = (rec.p - center) / radius;
return true; // 4번
}
C++
복사
천천히 식을 살펴보면
1.
우리가 구할 t의 크기를 구한 뒤
2.
그 t의 값이 t_min 보다 작거나, t_max 보다 크다면?
a.
우리가 구할 t값의 두번째 해를 가져와서
b.
다시 그 값을 t_min, t_max와 비교하는데
c.
이번에도 범위안에 들지 못하면 false!
3.
만약 범위안에 있는 값이라면! hit_record에 저장한 후
4.
return true!
코드를 살펴보면 크게 어렵지 않다는 것을 알 수 있다!
4) Front Faces Versus Back Faces
다음으로 나오는 내용도 크게 어렵지 않다!!
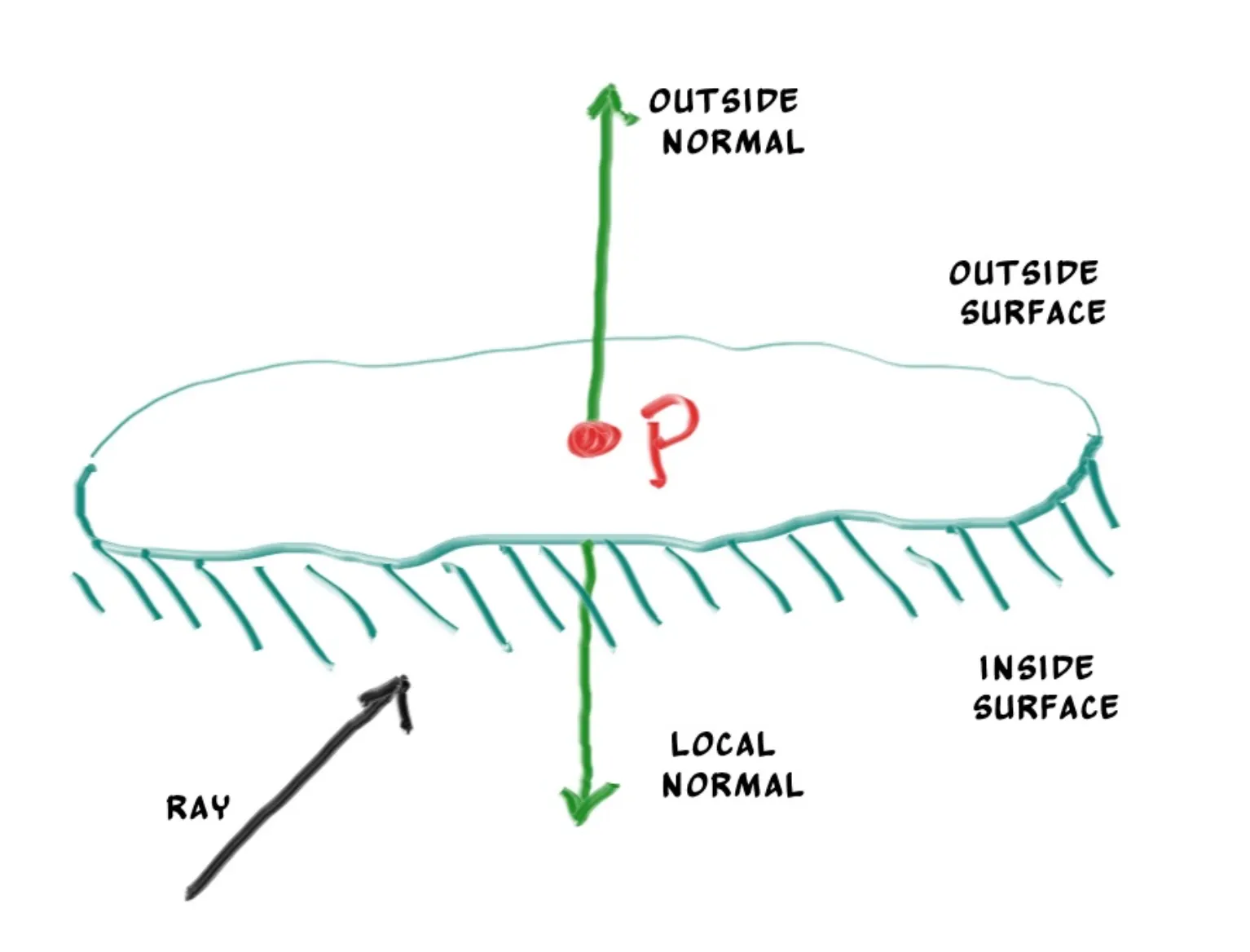
영어로 막 어렵게 써뒀지만 그냥 우리가 카메라를 설정했을 때, 카메라에서 쏘는 ray가 구 안쪽면을 보고 있는지, 바깥쪽 면을 보고 있는지에 대한 설명이다!
조금 더 자세하게 그림으로 그려보면 아래와 같다.
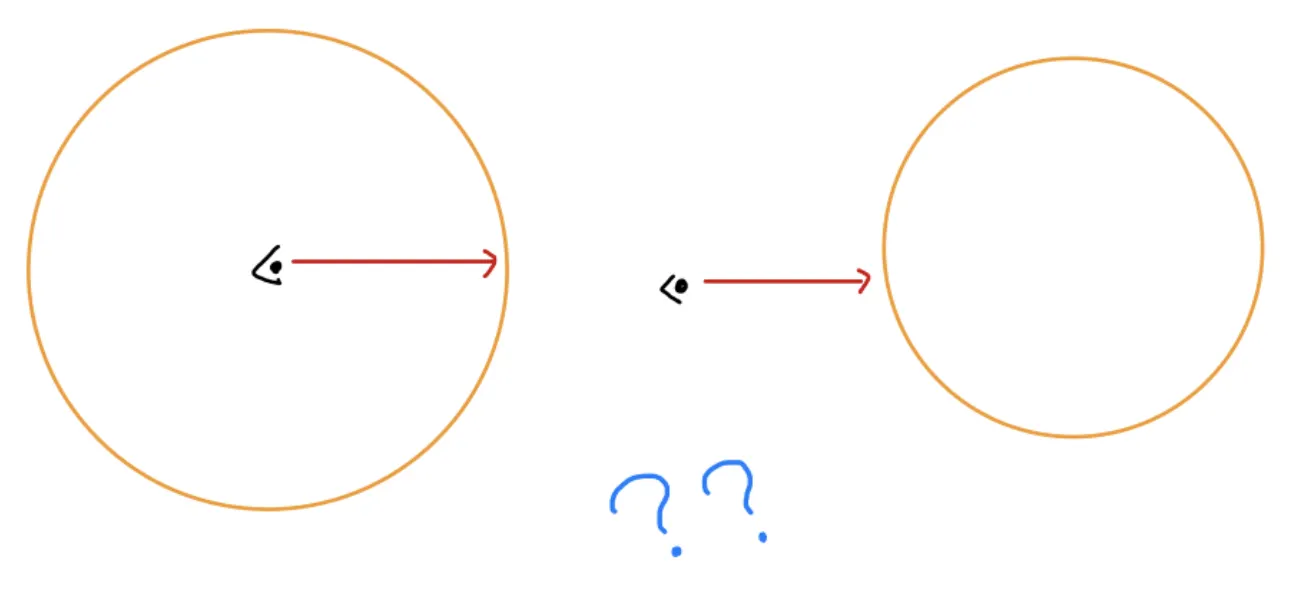
즉, 우리가 카메라에서 ray를 쐈는데 이 카메라가 구 안에 있는지, 밖에 있는지 지금은 판단이 안된다는 것이다!
하지만! 우리는 아주 간단하게 해결할 수 있다!
이걸 위해서 벡터에 대해 아주 상세하게 배우고 넘어왔기 때문이다!
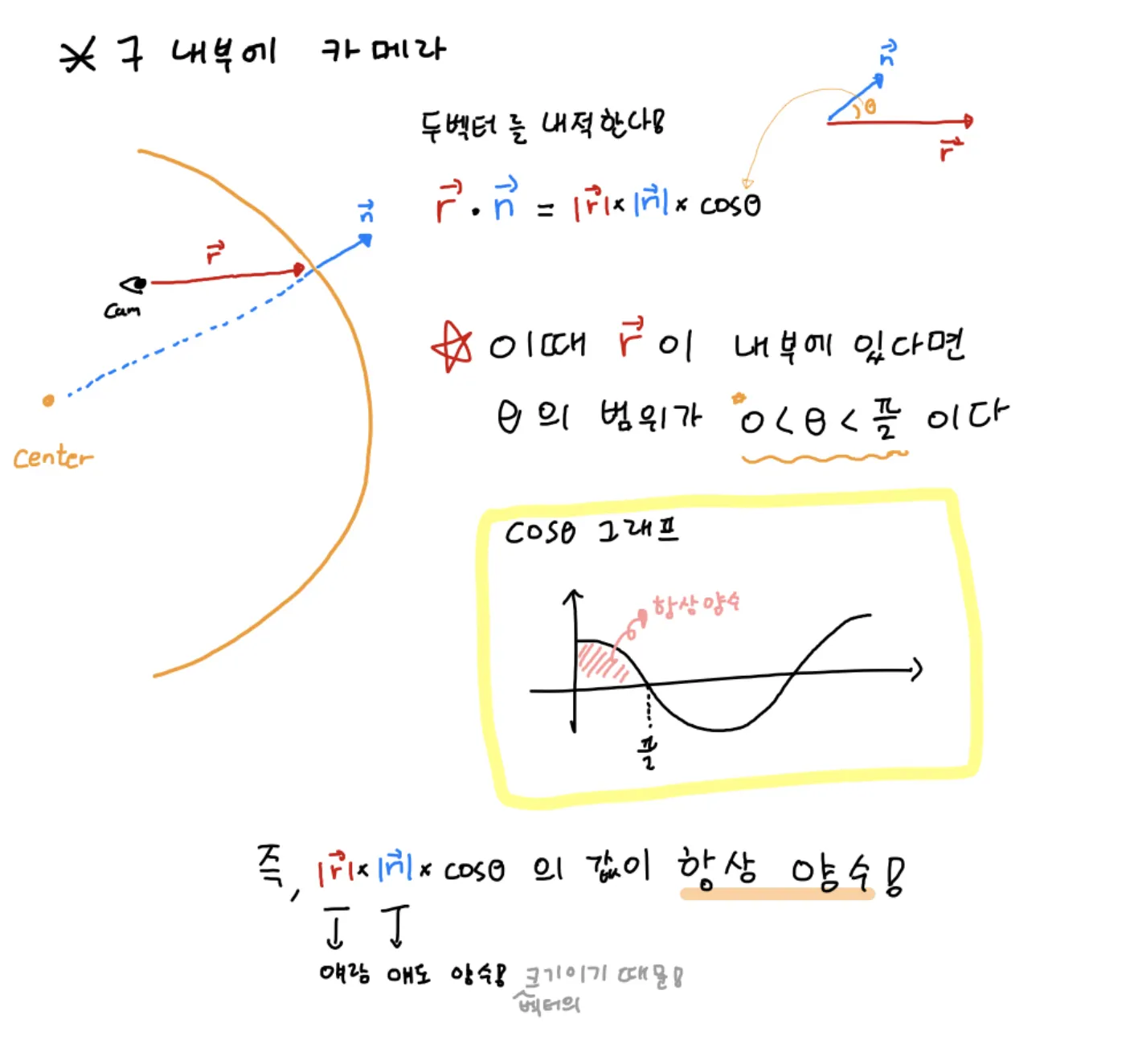
구 내부에 카메라가 있을 때!
이때, 카메라에서 쏘는 ray와 구와 ray가 부딪히는 지점에서의 법선벡터 n을 내적한다.
위 그림처럼 내적의 결과가 양수이면 ray가 구 내부에 있다는 것을 알 수 있다!
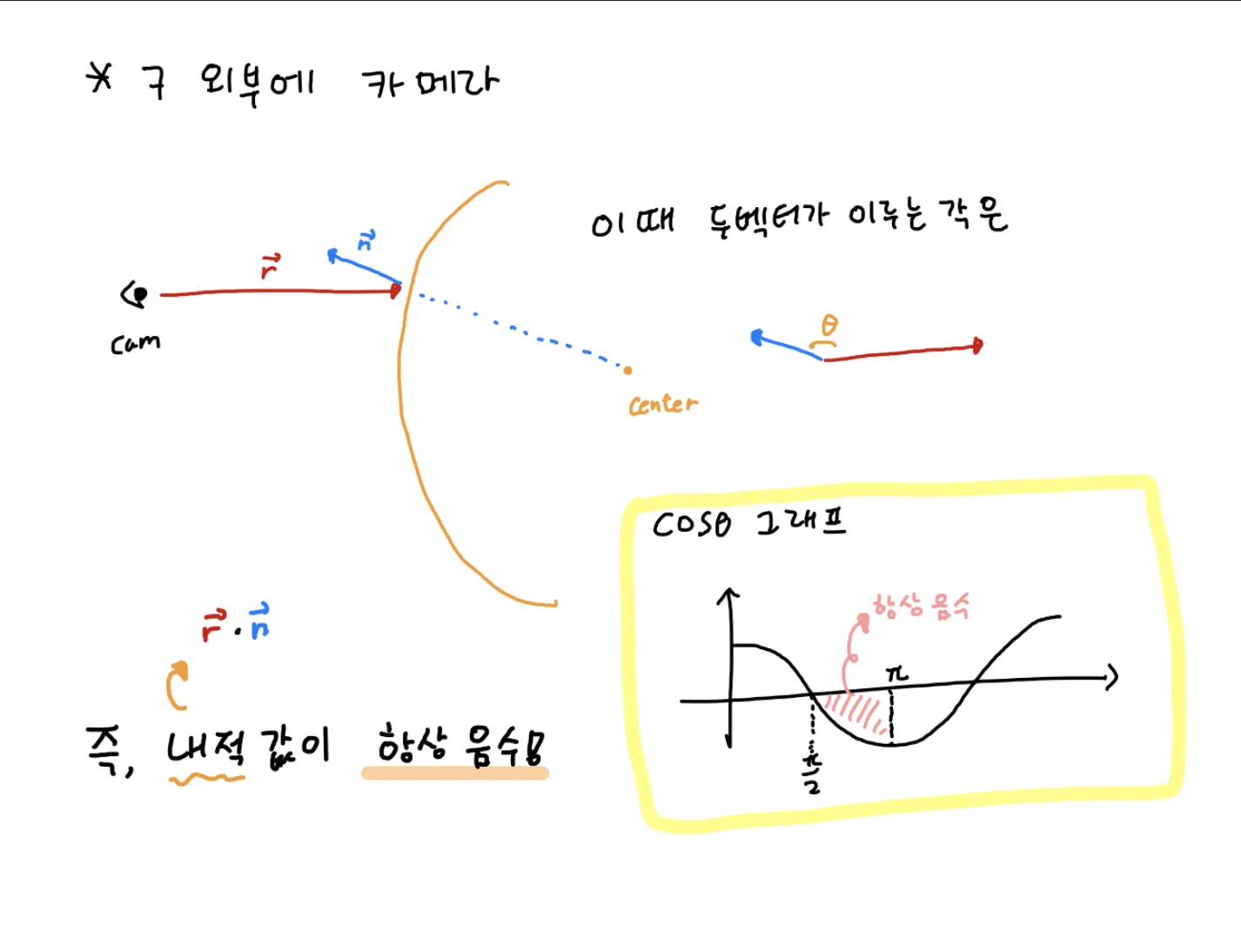
구 외부에 카메라가 있을 때!
이처럼 카메라가 구의 내부, 외부에 있냐에 따라 내적의 부호가 다르다는 것을 알 수 있다!
우리는 이것을 통해 카메라가 구 내부에 있을 때에는 구의 안쪽을 향하는 법선 벡터를 찾아야 한다!
즉, 내적 값이 양수가 나왔을 때(카메라가 구 내부에 있을 때), 기존 법선 벡터의 방향을 바꾸어 주는 것이다! 바로 모든 성분을 -로 바꾸는 방식으로 말이다.
bool front_face;
if (dot(ray_direction, outward_normal) > 0.0) {
// ray is inside the sphere
normal = -outward_normal; // 기존 법선벡터의 방향을 바꾸어준다!
front_face = false;
} else {
// ray is outside the sphere
normal = outward_normal;
front_face = true;
}
C++
복사
C에서는 아래와 같은 형식으로 만들어 줄 수 있다. 본인이 편한 코드를 사용하면 된다!
normal = vec(-normal.x, -normal.y, -normal.z);
C++
복사
아래 코드는 hit 함수에서 위의 식을 적용해 지점 p에서의 법선 벡터를 구해주는 부분이다.
bool sphere::hit(const ray& r, double t_min, double t_max, hit_record& rec) const {
...
rec.t = root;
rec.p = r.at(rec.t);
vec3 outward_normal = (rec.p - center) / radius;
rec.set_face_normal(r, outward_normal); // 법선벡터의 방향을 계산하는 부분
return true;
C++
복사
5) A List of Hittable Objects
하지만 아직 우리는 여러개의 오브젝트들을 어떻게 받아야 할지 배우지 않았다! 이제부터 이 문제를 어떻게 해결할지 알아보자!
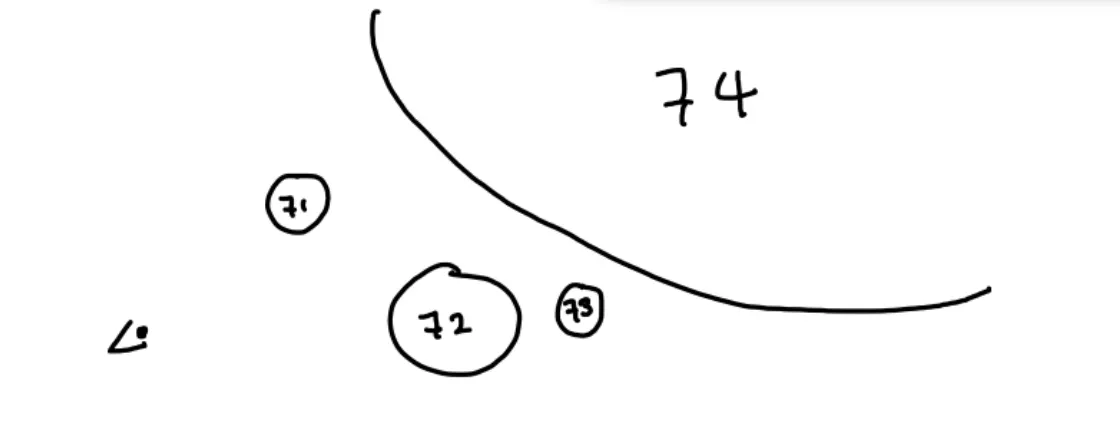
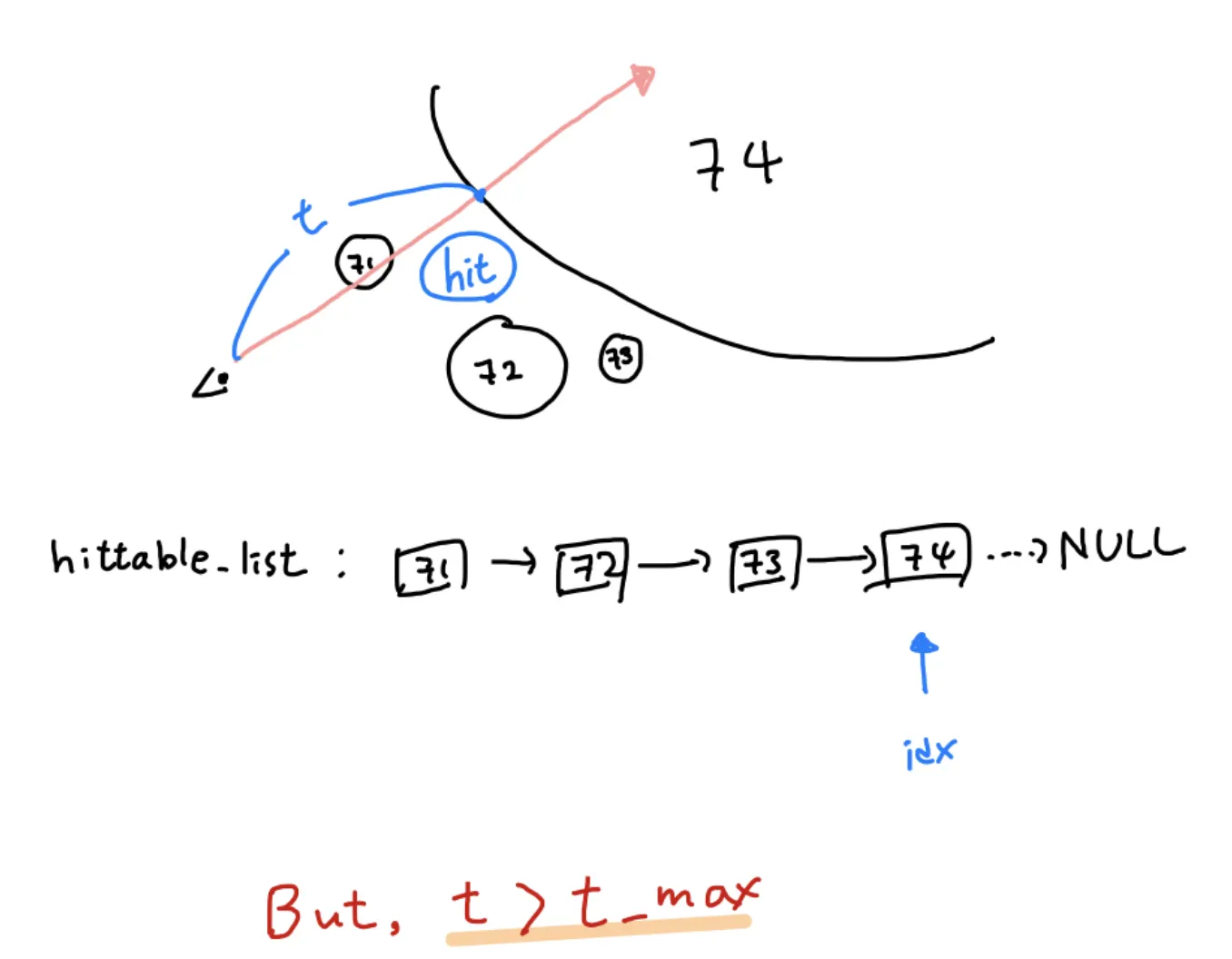
책에서는 여러개의 오브젝트들을 간단하게 리스트로 만들어 주었다. 리스트를 어떻게 활용하는지 아래 그림을 보자. 우선 4개의 구가 좌표상에 있다.
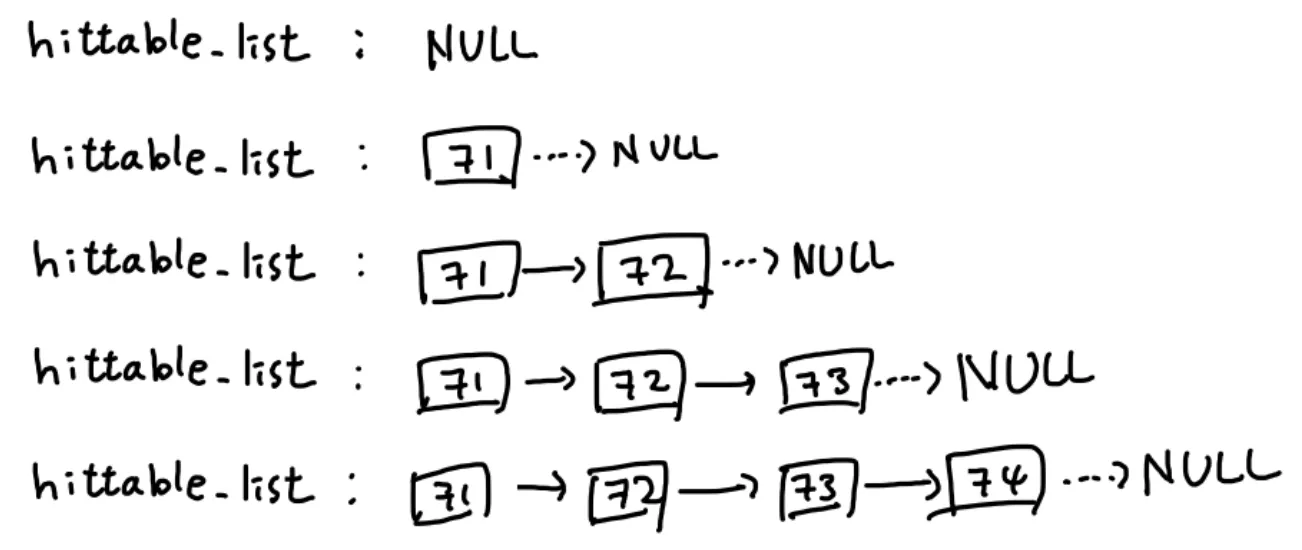
이때 우리는 구를 하나 추가할때마다 리스트에 하나씩 넣을 것이다. 아래의 그림처럼 말이다!
이제 ray를 한번 쏠때마다 이 리스트를 한번씩 돌면서 어떤 구에 맞는지 판단할 것이다.
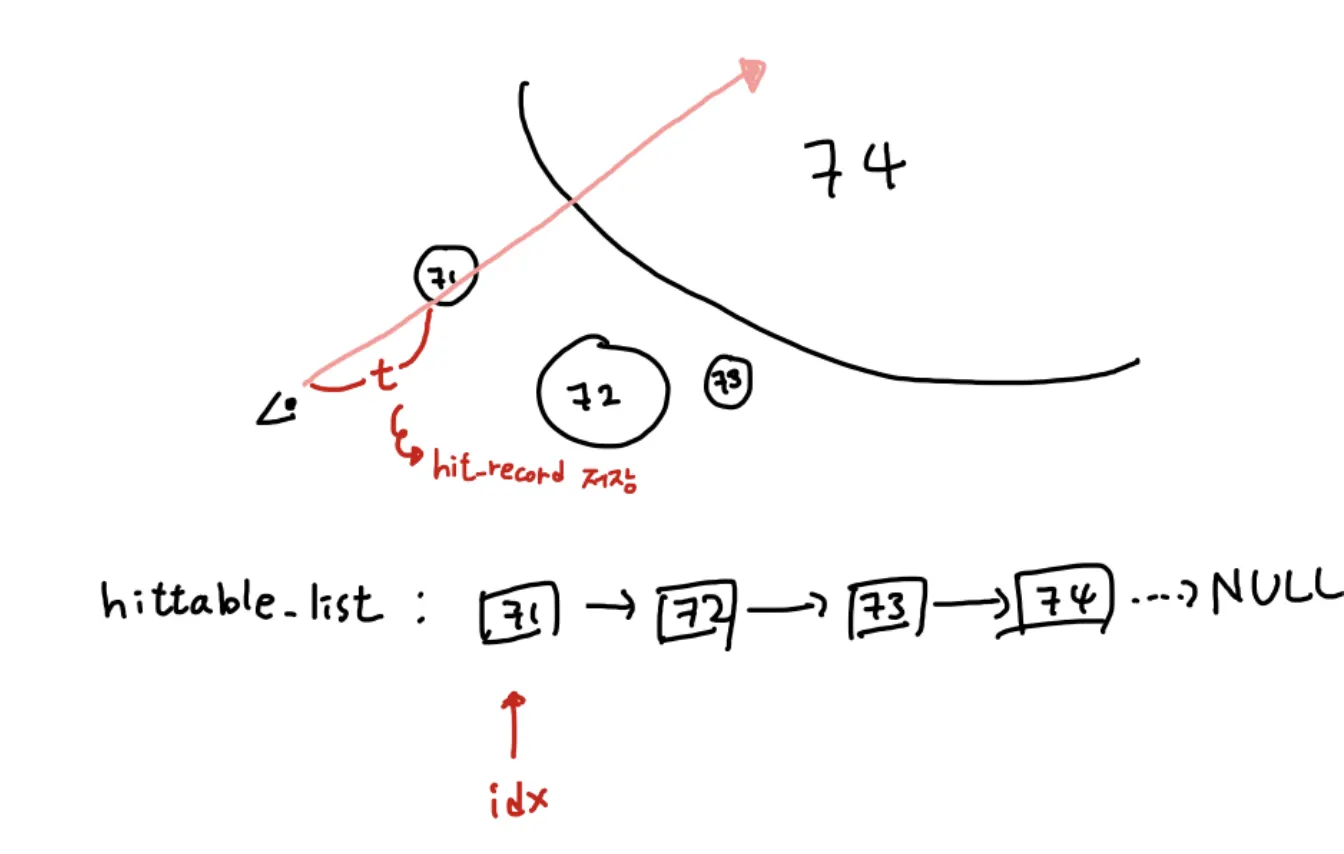
아래 그림처럼 핑크색 ray를 쐈다고 생각해보자! 우선 리스트의 첫번째 노드에 방문해 우리가 쏜 ray가 해당 object에 맞았는지 판단을 한다!
맞았다면 hit_record에 값을 저장하고 다음 노드로 넘어간다!
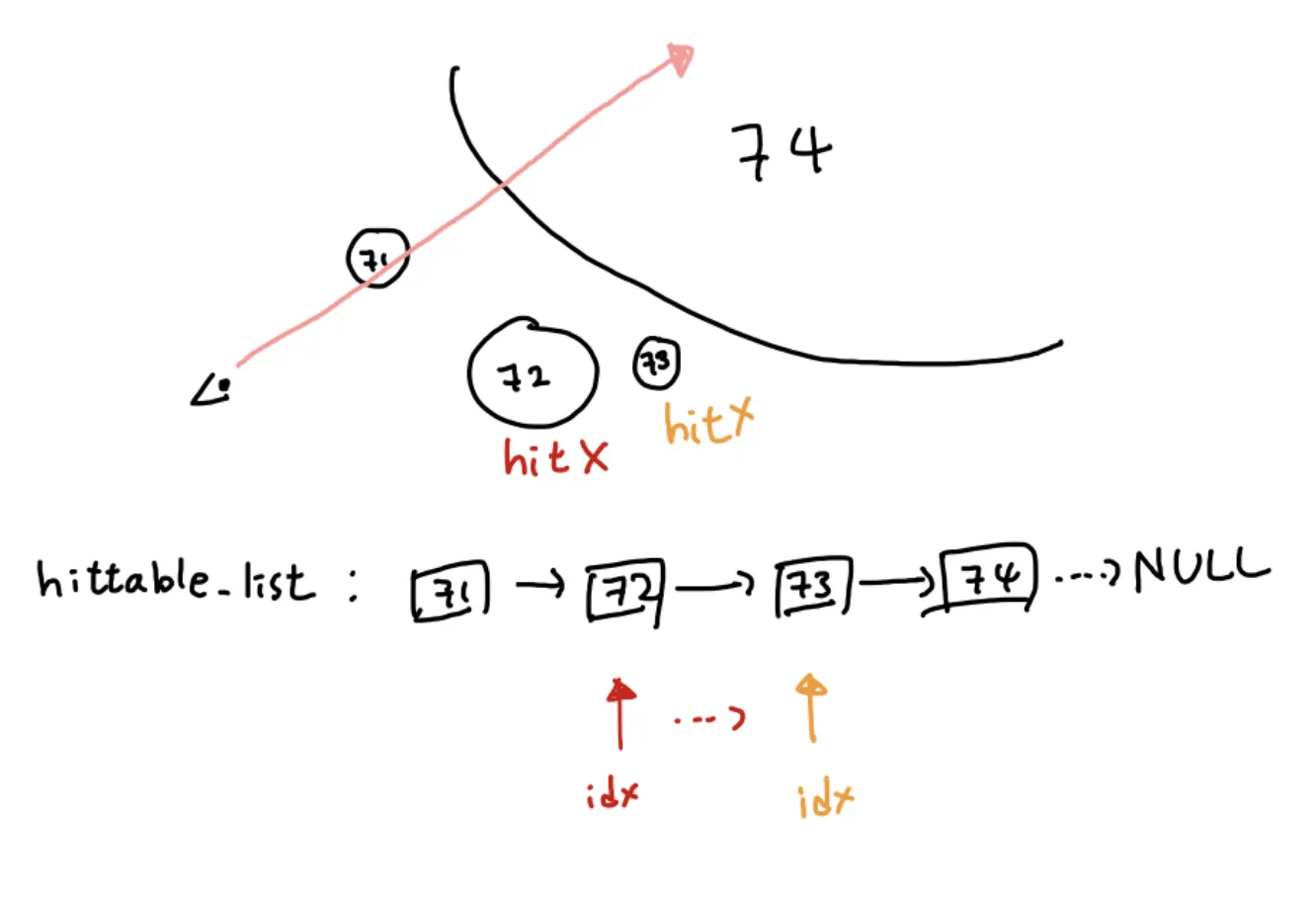
다음 노드로 넘어갔늗네 구2, 구 3은 ray와 부딪히지 않는다. 따라서 바로 구 4로 넘어간다!
이제 마지막 구4는 ray와 맞은 지점이 있기 때문에 hit_record에 값을 저장하려고 한다.
하지만! 우리가 이전에 hit_record에 저장할 때 t_max값보다 t가 크면 저장하지 않고 넘어가기로 했다!
구4 의 t 값이 이전의 t값보다 크기 때문에 저장하지 않고 넘어가게 된다.
이렇게 되면 우리는 object가 아무리 많더라도 어떤 지점이 가장 앞에 있는지 알 수 있게 되는 것이다!
6) Common Constants and Utility Functions
이부분은 살포시 넘어가도록 하겠다..ㅎㅎ
천천히 읽어보면 이해가 될 것이다!
Make!
이제 우리가 배웠던 내용을 토대로 코드를 작성해보자!!
기존의 코드를 수정하는 것이 대부분이기 때문에 크게 어렵지 않을 것이다!